Патент на изобретение №2152048

(54) СПОСОБ ОПРЕДЕЛЕНИЯ КООРДИНАТ МЕСТОПОЛОЖЕНИЯ, СОСТАВЛЯЮЩИХ ВЕКТОРА СКОРОСТИ, ДАЛЬНОСТИ И ТРАЕКТОРНЫХ ИЗМЕРЕНИЙ НАВИГИРУЮЩИМСЯ ОБЪЕКТОМ ПО НАВИГАЦИОННЫМ РАДИОСИГНАЛАМ КОСМИЧЕСКИХ АППАРАТОВ СПУТНИКОВЫХ РАДИОНАВИГАЦИОННЫХ СИСТЕМ

(57) Реферат:

Изобретение позволяет объекту определить свои координаты и составляющие вектора скорости, когда в зоне радиовидимости находятся три, два или один НИСЗ. Способ заключается в том, что параллельно или последовательно во времени принимают сигналы спутников и по принятым эфемеридным данным вычисляют проекции, модули N векторов-баз, значения направляющих косинусов, характеризующих направления N векторов-баз, значения косинусов углов между N векторами-базами и векторами, соединяющими вектора положения фазовых центров антенн спутников, вектор положения фазового центра антенны навигационной аппаратуры пользователей (НАП) объекта, значения косинусов их углов, скорости движения НИСЗ по орбите, радиусы и периоды орбит НИСЗ, измеряют дальности между фазовым центром НАП объекта и фазовыми центрами антенн спутников, используя измерения временных сдвигов между определенными кодовыми последовательностями, устанавливают систему линейных навигационных уравнений, дифференцируют уравнения по времени и с использованием измеренных радиальных скоростей, приращений дальностей, скоростей изменения приращений дальностей с применением ССН определяют координаты местоположения, значения составляющих вектора скорости фазового центра антенны НАП объекта путем решения соответствующих систем уравнений. Технический результат заключается в повышении точности. 3 з.п. ф-лы, 3 ил.

Изобретение относится к области спутниковой радионавигации, геодезии и может быть использовано навигирующимся объектом различного назначения для определения своих координат местоположения, составляющих вектора скорости, дальности и траекторных измерений.

Известен доплеровский разностно-дальномерный способ определения координат объектов и составляющих вектора скорости по навигационным радиосигналам навигационных искусственных спутников Земли (НИСЗ) спутниковых радионавигацонных систем (СРНС), основанный на измерениях разностей топоцентрических расстояний (дальностей) между объектом и тремя положениями одного и того же НИСЗ в последовательные моменты времени [1]. Практической реализацией известного способа являются российская СРНС 1-го поколения типа “Цикада” и американская СРНС “Транзит”. В них интегрирование доплеровского смещения частоты принятых от НИСЗ за интервал времени T позволяет определить число длин волн, укладывающихся в разность расстояний от навигирующегося объекта до трех положений одного и того же НИСЗ.

Недостатком известного способа являются:
дискретность навигационных сеансов;
низкая точность определения координат местоположения и составляющих вектора скорости в целом.

Известен также дальномерный способ, реализованный в СРНС 2-го поколения российской ГЛОНАСС (глобальная навигационная спутниковая система) и американской GPS (Global Navigation Satellite System), который принят в качестве прототипа. Геометрическим эквивалентом конечного алгоритма этого способа решения навигационной задачи является построение относительно используемых НИСЗ совокупности поверхностей положения, точка пересечения которых и является искомым положением навигирующегося объекта [2]. Для решения навигационной задачи минимально необходимый объем функциональных зависимостей, определяемый количеством одновременно видимых навигирующимся объектом НИСЗ, должен быть равен числу оцениваемых параметров. Число оцениваемых параметров равно четырем – три координаты местоположения, три составляющих вектора скорости и время.

Каждый спутник непрерывно передает собственные навигационные сообщения, содержащие информацию, на основе которой навигационная аппаратура пользователей (НАП), установленная на навигирующемся объекте, осуществляет измерения и расчеты, необходимые для решения навигационной задачи.

Навигационные сообщения содержат следующую информацию:
информацию о состоянии спутников, позволяющую пользователю сделать вывод о целесообразности использования данных, передаваемых спутникам для навигационных определений;
поправки к эталону времени спутника и данные об эфемеридах;
значения составляющих вектора скорости спутника;
параметры для введения поправок на задержку сигнала при распространении через ионосферу;
информацию альманаха об эфемеридах и состоянии всех остальных спутниках системы.

Формирование массивов служебной информации (время, эфемериды, составляющие вектора скорости спутников и т.д.), а также передачу (загрузку) их в память соответствующих НИСЗ производится наземными измерительными комплексами, контролирующими орбиты НИСЗ, расхождение шкал времени НИСЗ с системным временем и прогнозирование эфемериды каждого НИСЗ.

Эфемериды – значения координат НИСЗ в геоцентрической системе координат, рассчитанные для фиксированных моментов времени по результатам прогнозирования движения НИСЗ.

Используя указанную информацию, НАП выполняет измерения псевдодальности до выбранных НИСЗ и устанавливает функциональные зависимости между известными координатами НИСЗ и неизвестными координатами объекта. Определение координат местоположения объекта сводится к решению системы уравнений: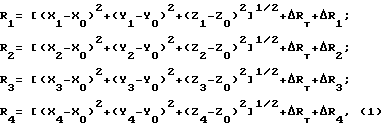

где R₁, . . . R₄ – результаты измерений, полученные с помощью следящих систем слежения за задержкой (ССЗ);
X_o, Y_o, Z_o – координаты объекта в геоцентрической прямоугольной системе координат, определяемые с помощью НАП;
X_i, Y_i, Z_i – координаты i-го НИСЗ, передаваемые в навигационном сообщении;
R_т – разница между истинной дальностью “объект – НИСЗ” и измеренной псевдодальностью, обусловленная сдвигом шкалы времени объекта относительно шкалы времени СРНС;
R_i – погрешности измерений, обусловленные условиями распространения навигационных сигналов, шумом НАП и т.д.

В результате решения этой системы уравнений определяются четыре неизвестных: три координаты местоположения объекта (X_o, Y_o, Z_o) и поправка R_т к его шкале времени (поправка к его часам).

Аналогичным образом, с использованием результатов измерений квазискоростей, определяются три составляющих вектора скорости объекта и поправка к частоте местного эталона частоты (МЭЧ), используемого для формирования шкалы времени:

где – составляющие вектора скорости i-го НИСЗ;
– результаты измерений, полученные с помощью следящей системы за несущей (ССН);
– составляющие вектора скорости объекта;
– разница между истинной скоростью и измеренной квазискоростью, обусловленной расхождением частот эталона частоты СРНС и эталона частоты объекта;
R_i – погрешности измерений, обусловленные условиями распространения навигационных сигналов, НАП и другими факторами.

Для устранения ионосферной задержки в известных способах используется аппаратурная компенсация с помощью двухчастотных измерений и компенсации с помощью поправок, рассчитываемых по априорным данным.

Недостатком известного способа, взятого в качестве прототипа, являются:
необходимость нахождения в поле зрения навигирующего объекта одновременно четырех НИСЗ;
погрешности, обусловленные геометрическим фактором (ГФ);
погрешности навигационных определений, обусловленные нестабильностью частот генераторов НИСЗ и опорных генераторов объектов, сдвигом шкал времени объектов относительно шкал времени НИСЗ, а также погрешности, вносимые вобуляцией времени начала следования кодированных последовательностей, специально введенной для снижения точности C/A-сигнала GPS.

Известный способ (прототип) характеризуется следующей совокупностью действий над принимаемыми спутниковыми радионавигационными сигналами:
прием N-канальной НАП, установленной на объекте, навигационных радиосигналов на двух частотах от четырех и более НИСЗ;
измерение псевдодальности от объекта до каждого видимого НИСЗ путем измерения фазового сдвига между псевдослучайными последовательностями (ПСП), сформированными каждым спутником, каждая из которых синхронизирована по собственному эталону времени, и ПСП, сформированной в месте приема (в НАП объекта);
измерение квазискорости путем измерения приращений дальностей на несущей частоте с использованием систем фазовой автоподстройки частоты (ФАПЧ);
определение координат местоположения объекта путем решения системы уравнений (1);
определение составляющих вектора скорости объекта путем решения системы уравнения (2).

Целью настоящего изобретения является определение координат, местоположения, составляющих вектора скорости, дальности и траекторных измерений навигирующимся объектом по навигационным радиосигналам СРНС путем приема навигационных радиосигналов от трех – одного НИСЗ СРНС ГЛОНАСС или GPS и повышение точности их определения.

Поставленная цель достигается за счет новой совокупности действий над принимаемыми спутниковыми навигационными радиосигналами и использования нового алгоритма решения навигационной задачи в векторном навигационном поле.

Векторное навигационное поле – функция на подмножестве трехмерного Евклидова пространства, значениями которого являются векторы, приложенные в точках этого подмножества. В рассматриваемом способе это совокупность векторов (направленных отрезков), соединяющих определенные положения НИСЗ на орбитах, и векторов, соединяющих положения НИСЗ и навигирующегося объекта в геоцентрической прямоугольной системе координат.

В основу предлагаемого способа положено знание пользователями СРНС в любое время суток, при любых метеорологических условиях, в любой точке Земного шара и околоземного пространства по принятой эфемеридной информации в составе навигационных сообщений радиосигналов НИСЗ в совпадающие моменты времени их векторов положения. Вычитание одноименных компонент этих векторов положения НИСЗ позволяет определить в геоцентрической системе координат (с началом в центре Земли и осевыми ортами, направленными соответственно по широте на восток, по меридиану на север и вертикально вверх по отношению к поверхности Земли) проекции базовый линий (векторов), соединяющих положения НИСЗ на орбитах, расстояния между ними, а также направляющие косинусы (углы ,,, характеризующие положения векторов-баз (расстояний) в пространстве.

Но возможно также последовательное во времени положение одного и того же НИСЗ рассматривать как различные НИСЗ, образующие соответствующие вектора-баз, учитывая при этом перемещение НИСЗ в интервале измерений.

Знание направляющих косинусов, характеризующих направления векторов-баз в пространстве, и результатов измерений, проведенных НАП, установленной на объекте, позволяет определить координаты местоположения, составляющие вектора скорости, дальности между фазовым центром антенны объекта и фазовыми центрами антенн НИСЗ и провести траекторные измерения.

Решение навигационной задачи в векторном поле позволяет исключить важный источник погрешностей, связанный с геометрическим фактором определения положения объекта в пространстве.

Геометрический фактор (ГФ) – аналитическая связь погрешностей определения горизонтальных (X, Y) и вертикальной координат объектов с инструментальными (без ионосферы) погрешностями до выбранных НИСЗ. В каждом случае умножение величины среднеквадратической погрешности измерения дальности от объекта до спутника на соответствующее значение ГФ дает соответствующую среднеквадратическую погрешность определения положения объекта. Очевидно, что малые значения ГФ указывают на благоприятное с точки зрения решения навигационной задачи геометрическое расположение спутников. Пороговые значения ГФ определения положения в пространстве PDOP СРНС ГЛОНАСС и GPS составляют 2,5 PDOP 6 (PDOP – Position Delution of Precision).

Для решения навигационной задачи в векторном навигационном поле в состав навигационных сообщений, загружаемых в память каждого НИСЗ ГЛОНАСС и GPS наземными измерительными комплексами для передачи ее навигирующимся объектам, вводят также рассчитанные по результатам прогнозирования значения модулей векторов-баз (расстояний, пройденных НИСЗ за интервалы времени, равные секунда/n, n секунд, где n = 1, 2, 3…) и значения их направляющих косинусов в геоцентрической системе координат. Геометрическая интерпретация предлагаемого способа иллюстрируется на фиг. 1, 2, 3.

Сущность предлагаемого способа поясняется на примере одного НИСЗ и на примере первого, второго и третьего мерных интервалов. На фиг. 1, 2 точками t, t₁, t₁^*, t₂, t₂^* t₂^*, t₃, t₃^*, t₄ обозначены положения фазового центра антенны НИСЗ, являющиеся границами отсчетов навигационного параметра.

Значения модулей векторов-баз и направляющих косинусов определяются по данным, передаваемым каждым спутником в навигационном сообщении как: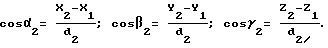






где X, Y, Z, X₁, Y₁, Z₁, X₂, Y₂, Z₂, X₃, Y₃, Z₃ – координаты фазового центра антенны НИСЗ в моменты времени t, t₁, t₂, t₃ соответственно.

Разность дальностей (фиг. 2) R₁, R₂, R₃ определяется по результатам измерения приращений дальностей с использованием системы слежения за несущей (ССН), предназначенной для слежения за фазой несущей, выделения информации и измерения доплеровского сдвига частоты.

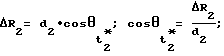Для определения местоположения фазового центра антенны объекта в трехмерной системе координат, осуществляется прием сигналов от трех НИСЗ, устанавливаются три линейных функциональные зависимости между известными значениями направляющих косинусов вектора-баз и неизвестными значениями направляющих косинусов векторов положения фазового центра антенны НАП объекта или устанавливаются три аналогичных функциональных зависимостей для одного и того же НИСЗ для трех последовательных во времени его положений на орбите и решается затем система из трех линейных уравнений с тремя неизвестными X₀, Y₀, Z₀ [3].

Аналогичным образом с использованием результатов измерений радиальных скоростей, дальностей с помощью ССН, ССЗ НАП соответственно и определений разностей радиальных скоростей, разностей дальностей определяют три составляющие вектора скорости фазового центра антенны НАП объекта:

или

где 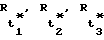– дальности от фазового центра антенны НАП объекта до фазовых центров антенн первого, второго и третьего спутников или фазового центра антенны одного и того же спутника, находящегося в серединах мерных интервалов, для трех последовательных во времени положений его на орбите, измеренные с использованием ССЗ ПСП;
– радиальные скорости, разности радиальных скоростей, разности дальностей, измеренные с использованием ССН;
направляющие косинусы векторов, соединяющие положения фазовых центров антенн спутников, находящихся в серединах мерных интервалов, и положения фазового центра антенны НАП объекта.

Для более точного определения местоположения, составляющих вектора скорости фазового центра антенны объекта и определения расстояния (дальности) между фазовым центром антенны НИСЗ и фазовым центром антенны объекта, осуществляется прием навигационных сигналов от трех НИСЗ или сигнала одного и того же НИСЗ для трех последовательных во времени положений его на орбите, устанавливаются шесть линейных функциональных зависимостей между известными значениями направляющих косинусов векторов-баз и неизвестными значениями направляющих косинусов векторов положения фазового центра антенны НАП и решается система из шести линейных уравнений с шестью неизвестными X₀, Y₀, Z₀, :

где
cos₁= cos₁cos₂+cos₁cos₂+cos₁cos₂;
cos₂= cos₂cos₃+cos₂cos₃+cos₂cos₃;
cos₃= cos₃cos₄+cos₃cos₄+cos₃cos₄;

– дальности между фазовым центром антенны НАП навигирующего объекта и фазовыми центрами антенн (антенны) НИСЗ, соответствующие их определенным положениям на орбите и являющимися границами отсчета навигационного параметра.

Составляющие вектора скорости навигирующего объекта определяются путем решения системы уравнений, получаемых после дифференцирования уравнения системы (6) по времени.

Из треугольника t₃ П t₂ (фиг. 3), используя теорему синусов, определяются значения расстояний (дальностей) между фазовым центром антенны объекта и фазовым центром антенны спутника, находящегося в точках t₂, t₃, соответственно.

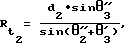где угол t₃ П t₂ равен
Зная 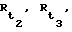и значения направляющих косинусов векторов-баз d₂, d₃, d₄, определяемые как отношения разностей одноименных компонент векторов положения фазовых центров антенны НИСЗ, определяющих начало и конец баз (мерных интервалов) к расстояниям между ними (между положениями фазовых центров антенны НИСЗ на орбите), находят функциональные зависимости (систему уравнений), позволяющие по двум или по одному и тому же НИСЗ, по двум его положениям на орбите, без использования результатов измерений значений 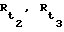с помощью ССЗ ПСП определить с высокой точностью координаты местоположения и составляющие вектора скорости объекта.

Система уравнений запишется следующим образом:




Значения составляющих вектора скорости фазового центра НАП объекта определяются путем решения систем уравнений, получаемых после дифференцирования систем (7), аналогичных системам (4), (5).

Определение направления “фазовый центр антенны НИСЗ – фазовый центр антенны НАП (cos) фиг. 1, 2, основано на прямолинейном распространении радиоволн в однородной среде и сводится к определению направления прихода излучаемых радиоволн НИСЗ путем сравнения фаз колебаний, возбуждаемых в антенне НАП объекта. Предлагаемый способ основан на измерении разностей фаз колебаний несущих частот (приращений дальностей) с использованием ФАПЧ ССН на мерном интервале.

Сущность измерений предлагаемого способа состоит в том, что разнесенные в пространстве положения фазовых центров антенн НИСЗ, соответствующие определенным мерным интервалам вследствие движения НИСЗ, образуют измерительные базы d, характерные для линейных интерферометров.

НАП навигирующегося объекта, принимая навигационные радиосигналы НИСЗ, оценивают разность их хода для одного – трех и более положений фазовых центров антенн НИСЗ и фазовым центром антенны НАП.

Разность фаз (приращений фаз) напряжений навигационных радиосигналов НИСЗ, разность дальностей определяется следующим образом (фиг. 2).

где – длина волны; = 3б1415…

Малость базы необходима в этом случае как условие практической параллельности направлений от НИСЗ к антенне НАП. С другой стороны, для уменьшения случайных составляющих погрешностей отсчета разностей фаз необходимо увеличивать размеры базы по сравнению с длиной волны.

Радиальная скорость движущегося НИСЗ относительно объекта, полагая, что объект неподвижен, пропорциональна косинусу угла , составленного вектором скорости НИСЗ V с направлением от объекта в точку наблюдения (НИСЗ) [1].

С другой стороны, радиальная скорость 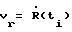выражается через доплеровский сдвиг (F_д) следующим образом: , где – длина волны навигационного сигнала, излучаемого НИСЗ.

Следовательно,
Согласно фиг. 2 для мерного интервала (t₃ – t₂)

Скорость движения НИСЗ по круговой орбите радиусом (R₃ + H), где H – высота орбиты, согласно [4] определяется выражением

где – коэффициент, равный произведению гравитационной постоянной на массу Земли.

С точностью, достаточной для решения ряда простейших задач, можно считать, что = 3,986 10⁵ км³/сек².

Очевидно, что период обращения НИСЗ (обозначим его через P) будет определяться соответственно из выражения

В соответствии с фиг. 1, 2 угол ₃, равный как , позволяет с использованием теоремы, синусов определить дальность между фазовым центром антенны НАП объекта и фазовыми центрами антенн НИСЗ для любого мерного интервала с использованием только результатов измерений приращений дальностей с помощью ССН.

Таким образом, предложенный способ одновременно позволяет проводить в беззапросном режиме высокоточные траекторные измерения как с использованием сети наземных измерительных комплексов, так и автономно на борту каждого НИСЗ (самоопределение) с использованием наземных навигационных точек (радиомаяков) и других искусственных спутников Земли в качестве орбитальных навигационных точек. Очевидно, что в этом случае прогнозирование движется НИСЗ для решения навигационной задачи не требуется.

Отличительные признаки предложенного способа:
последовательный или направленный во времени прием НАП объекта навигационных радиосигналов от трех НИСЗ;
определение по эфемеридным данным проекции N векторов-баз, соединяющих два положения фазовых центров антенн НИСЗ на орбите, определяемые мерными интервалами, путем вычитания одноименных компонент векторов положения фазовых центров антенн НИСЗ;
определение по принятым эфемеридным данным модуля N векторов-баз для N+1 положений их на орбите, соединяющих два положения фазовых центров антенн спутников и определяемых мерными интервалами, как корни квадратные из сумм квадратов проекций векторов-баз на оси геоцентрической системы координат и определение значений направляющих косинусов, характеризующих направления векторов-баз в пространстве, как отношение соответствующих проекций к значениям модулей векторов-баз;
определение значений косинусов углов между N векторам-баз и векторами, соединяющими вектора положений фазовых центров антенн спутников, находящихся в серединах баз, и вектор положения фазового центра антенны НАП объекта с интерферометрическим использованием измерений приращений дальностей с помощью ССН как отношение приращений дальностей к значениям модулей векторов-баз;
измерение дальностей между фазовым центром антенны НАП объекта и фазовыми центрами антенн спутников, находящихся в серединах N-мерных интервалов, путем измерений временных сдвигов между кодовыми последовательностями, сформированными спутниками, и кодовой последовательностью, сформированной в месте приема с помощью ССЗ, каждая из которых синхронизирована по собственному эталону времени [5];
прием НАП объекта навигационного сигнала от одного и того же НИСЗ для (N+1) последовательных во времени его положений на орбите и определение по принятым эфемеридным данным модуля N-векторов-баз, соединяющими два положения фазовых центров антенн НИСЗ и определяемые мерными интервалами, как корни квадратные из сумм квадратов проекций векторов-баз на оси геоцентрической системы координат и определение значений направляющих косинусов, характеризующими направление векторов-баз в пространстве, как отношение соответствующих проекций к значениям модулей векторов-баз;
измерение дальностей между фазовым центром антенны НАП объекта и фазовым центром антенны одного и того же НИСЗ, находящегося в серединах N-мерных интервалов путем измерений временных сдвигов между кодовой последовательностью сформированной НИСЗ и кодовой последовательностью, сформированной в месте приема с помощью ССЗ, каждая из которых синхронизирована по собственному эталону времени;
установление по результатам навигационных измерений системы из трех линейных функциональных зависимостей (навигационных уравнений) между известными значениями направляющих косинусов векторов-баз и неизвестными значениями направляющих косинусов векторов, соединяющими вектора положения фазовых центров антенн спутников (фазового центра антенны одного и того же спутника для N-мерных интервалов) и вектор положения фазового центра антенны НАП объекта и определение координат местоположения фазового центра НАП объекта путем решения системы уравнений;
дифференцирование по времени трех установленных функциональных зависимостей (3), выраженные через направляющие косинусы векторов-баз, известные координаты местоположения фазовых центров (фазового центра) антенн (антенны) НИСЗ и неизвестными координатами фазового центра антенны НАП объекта, а также через измеренные дальности между фазовыми центрами антенн НИСЗ и фазовым центром НАП объекта, а также через косинусы углов между векторами-баз и векторами, соединяющими вектора положения фазовых центров антенн НИСЗ, находящихся в серединах мерных интервалов, и вектор положения фазового центра антенны НАП объекта;
определение по эфемеридным данным значения косинусов углов и значения углов, характеризующих направление N векторов-баз в пространстве как отношения соответствующих проекций векторов-баз на оси геоцентрической системы координат к значениям модулей векторов-баз и как арки косинусов отношений, а также значения углов между смежными векторами-баз, соответствующие определенным мерным интервалам из уравнений и как разности значений углов, характеризующих их направление в пространстве;
определение с интеферометрическим и тригонометрическим использованием измерений приращений дальностей с помощью ССН значений косинусов углов, значения углов между векторами-баз и векторами, соединяющими вектора положения фазовых центров антенн спутников (фазового центра антенны одного и того же спутника для N-мерных интервалов), находящихся в точках пересечения смежных векторов-баз, и вектора положения фазового центра антенны НАП объекта, как отношение соответствующих приращений дальностей к значениям модулей векторов-баз и как арки косинусов отношений;
установление системы из шести функциональных зависимостей (навигационных уравнений) между известными значениями направляющих косинусов векторов-баз и неизвестными значениями направляющих косинусов векторов, соединяющими вектора положения фазовых центров антенн НИСЗ (фазового центра антенны одного и того же спутника для N-мерных интервалов) и вектора положения фазового центра антенны НАП объекта;
определение координат местоположения, значения составляющих вектора скорости фазового центра антенны НАП объекта и дальностей между фазовыми центрами антенн (фазовым центром) НИСЗ и фазовым центром антенны НАП объекта путем решения систем уравнений;
дифференцирование по времени шести установленных навигационных уравнений (5), выраженные через направляющие косинусы векторов-баз, известные координаты местоположения фазовых центров (фазового центра) антенн (антенны) НИСЗ и неизвестные координаты фазового центра антенны НАП объекта, а также через вычисленные с интерферометрическим и тригонометрическим использованием измерений приращений дальностей с помощью ССН дальностей между фазовыми центрами антенн и косинусы углов между векторами-баз и векторами, соединяющими вектора положения фазовых центров антенн НИСЗ, находящихся в точках пересечения смежных векторов-баз и вектора положения фазового центра антенны НАП объекта;
определение координат местоположения и значения составляющих вектора скорости фазового центра антенны НАП объекта путем решения систем уравнений (3), (4), (5);
последовательный или параллельный во времени прием НАП объекта навигационных радиосигналов от двух НИСЗ, измерение дальностей между фазовым центром антенны НАП объекта и фазовыми центрами антенн НИСЗ, находящихся в точках пересечения смежных векторов-баз, для (N+1) его положений на орбите по фазе несущей с тригонометрическим использованием измеренных приращений дальностей с помощью ССН путем использования теоремы синусов и установления системы из четырех линейных функциональных зависимостей;
установление по результатам навигационных измерений и вычислений по двум или по одному и тому же НИСЗ для (N+1) его положений на орбите системы линейных функциональных зависимостей (навигационных уравнений) между известными значениями направляющих косинусов векторов-баз и неизвестными значениями направляющих косинусов векторов, соединяющими вектора положения фазового центра антенны НИСЗ и вектора положения фазового центра антенны НАП объекта;
дифференцирование по времени четырех установленных функциональных зависимостей (7), выраженных через направляющие косинусы векторов-баз, известные координаты местоположения фазовых центров антенн (антенны) НИСЗ, находящихся (находящегося) в точках пересечения смежных векторов-баз, и неизвестные координаты местоположения фазового центра антенны НАП объекта, а также через вычисленные дальности по фазе несущей с интерферометрическим и тригонометрическим использованием приращений дальностей с помощью ССН, косинусы углов между векторами-баз и векторами, соединяющими вектора положения фазовых центров антенн НИСЗ и вектор положения фазового центра антенны НАП объекта;
определение координат местоположения и значения составляющих вектора скорости фазового центра антенны НАП объекта путем решения системы уравнений;
определение скорости движения НИСЗ по орбите как отношение произведений осредненных на N мерных интервалах значений доплеровских сдвигов частоты, длин волн излучаемых навигационных радиосигналов и расстояний между двумя положениями фазовых центров антенн НИСЗ (фазового центра антенны НИСЗ), соответствующих началам и концам N мерным интервалам, к значениям приращений дальностей на мерных интервалах, измеренных с помощью ССН;
определение радиуса орбиты НИСЗ как квадрат отношения произведения осредненных на мерных интервалах значений доплеровского сдвига частоты, длин волн излучаемых навигационных сигналов и расстояний между двумя положениями фазовых центров антенн НИСЗ (фазового центра антенны НИСЗ), соответствующих началам и концам мерных интервалов к значениям приращений дальностей на мерных интервалах, умноженные на коэффициент, равный произведению гравитационной постоянной на массу Земли;
определение значений углов между N векторами положения фазовых центров антенн (антенны) НИСЗ, находящихся в серединах мерных интервалов, и N векторами, соединяющими вектора положения фазовых центров антенны НАП объекта как разность между значениями углов между N векторами-баз и векторами, соединяющими вектора положения фазовых центров антенны НАП объекта и девятью-десятью градусами;
определение дальностей между фазовым центром антенны НАП объекта и фазовыми центрами антенн НИСЗ путем использования теоремы синусов и решения систем навигационных уравнений;
определение периода орбиты НИСЗ как куб отношения произведения осредненного на мерном интервале значений доплеровских сдвигов частоты, длины волн излучаемого навигационного радиосигнала и расстояния между двумя положениями фазовых центров антенн НИСЗ (фазового центра антенны НИСЗ), соответствующие началу и концу мерного интервала, к значению приращения дальности на мерном интервале, измеренному с помощью ССН, умноженному на два радиан и коэффициент, равный произведению гравитационной постоянной на массу Земли;
расчет по эфемеридным данным и результатам прогнозирования движения НИСЗ наземными измерительными комплексами значений модулей и значения направляющих косинусов векторов-баз, соответствующие определенным мерным интервалом, закладка их в память каждого НИСЗ и размножение их на борту НИСЗ на текущие мерные интервалы.

Технический результат использования предложенного технического решения заключается в следующем.

Предложенный способ позволяет навигирующимся объектам, использующим НАП СРНС (пользователям СРНС), определить свои координаты местоположения и составляющие вектора скорости, когда в зоне радиовидимости объекта находятся три или один НИСЗ вместо четырех, как это реализовано в известном способе. НИСЗ американской GPS излучают одновременно два радиоанавигационных сигнала: сигнал P-кода, предназначенный для военных пользователей с санкционированным доступом к системе и обеспечивающий высокую точность определения местоположения, и сигнал C/A-кода, предназначенный для использования гражданскими пользователями и обеспечивающий меньшую точность местоопределения. Основной составляющей погрешности при измерении псевдодальности с использованием сигнала C/A-кода гражданскими пользователями является регулярная составляющая, вносимая вобуляцией времени начала следования кодированных последовательностей, специально введенная для снижения точности. Она составляет 30 м [6], использование предлагаемого способа позволит гражданским пользователям GPS, ГЛОНАСС, принимая навигационные сигналы C/A-кода от одного НИСЗ, определить координаты местоположения и составляющие вектора скорости с точностью не ниже, чем военные пользователи по сигналам P-кода.

Высокая точность достигается:
1. За счет отказа гражданскими пользователями использовать C/A-код для измерения псевдодальности, т.е. отказа использования псевдодальности в качестве навигационного параметра. Это дает повышение точности навигационных определений уже как минимум на 30 м. В предложенном способе в качестве навигационного параметра используются приращения дальностей, измеренные по фазе несущей с помощью ССН. Погрешности измерений приращений дальностей (погрешности измерений приращений фаз, обусловленные доплеровским сдвигом частот) на частотах СРНС ГЛОНАСС, GPS при соотношении сигнал/шум = C/N₀=30 дБ и B_CCH = 20 Гц составляют 6,2 мм [7, стр. 175]. При этом пределы измерений приращений фаз не ограничиваются интервалами длиной 2, т.е. нет проблемы многозначности измерений приращений фаз. Поскольку при использовании предложенного способа навигационных определений пользователям необходим один НИСЗ, то могут быть использованы антенны НАП с коэффициентом усиления не 0 дБ, как при известном способе, а 10 дБ. В этом случае погрешности измерений приращений дальностей не превысят ~ 2 мм.

2. За счет использования нового алгоритма решения навигационной задачи в векторном поле исключается источник погрешностей навигационных определений, обусловленный ГФ. Погрешности навигационных определений снижаются в (2-6) раз.

3. За счет относительных определений модулей векторов-баз и их направляющих косинусов, положительной особенностью которых является то, что при их использовании ряд погрешностей, имеющих систематический характер, скомпенсируется. Погрешности определений модулей векторов-баз на мерном интервале, равном 1 с, не превышают 100 мм, а погрешности углов ,,, характеризующие направление векторов-баз в пространстве, составляют, соответственно, 2,510^-6 рад. Следовательно, погрешности косвенных измерений дальностей между фазовым центром антенны НИСЗ и фазовым центром антенны НАП с тригонометрическим использованием измерений приращений дальностей в предложенном способе составят 7,7 м.

Учитывая также, что новый алгоритм решения навигационной задачи исключает источник погрешностей навигационных определений за счет ГФ, предельная погрешность ( 3 ) навигационных определений предложенного способа на секундном, 10-секундном мерных интервалах составят 23,1 и 7,3 метра, соответственно.

Использование предложенного способа гражданскими пользователями американской GPS позволит не только обойти специально и искусственно введенный санкционированный доступ к навигационному сигналу P-кода, обеспечивающему высокую точность навигационных определений, и загрубление по точности навигационного сигнала C/A-кода, но и обеспечить пользователям навигационные определения по фазе несущей навигационного сигнала с более высокой точностью, нежели военными пользователями по сигналу P-кода.

Вследствие того что предложенный способ вобрал в себя методики относительных измерений и определений, повысится вероятность, что НАП обеспечит пользователей СРНС информацией, достаточной для решения целевых задач с требуемой точностью, т.е. повысится доступность СРНС.

Доступность системы – это вероятность того, что в любое время и в любой точке пространства навигационная система обеспечивает пользователя информацией, достаточной для определения местоположения с требуемой точностью.

Штатные подсистемы космических аппаратов (НИСЗ) СРНС российской ГЛОНАСС и американской GPS имеют в своем составе по 24 спутника. При использовании предложенного способа, когда пользователи могут навигироваться по одному спутнику, для обеспечения глобального навигационного поля СРНС ГЛОНАСС и GPS достаточно подсистем из 9, 12 космических аппаратов, соответственно. В этом случае для поддержания эксплуатационного состояния спутниковых систем высвобождаются огромные финансовые ресурсы.

В настоящее время в отечественной и зарубежной НАП СРНС ГЛОНАСС и GPS широко используются измерения доплеровских сдвигов частоты, основанные на измерениях приращений дальностей на частоте несущей с использованием ССН, предназначенных для слежения за фазой несущей [2], [7]. Поэтому для реализации предложенного способа нет никаких проблем, остается только использовать измеряемые в эксплуатируемой НАП приращения фаз (приращения дальностей).

Глобальные СРНС ГЛОНАСС и GPS являются в настоящее время одними из основных систем, обеспечивающих высокую точность навигационных определений как военного, так и гражданского сектора пользователей. К концу нынешнего столетия системы смогут заменить все другие радионавигационные средства для обслуживания пользователей. Число областей применения НАП ГЛОНАСС и GPS впечатляюще велико. При современной технологии производства интегральных схем НАП ГЛОНАСС, GPS вскоре станут столь миниатюрными и дешевыми, что их сможет носить с собой каждый человек, а значит, определять в любое время, где он находится и “как отсюда выбраться”. НАП станет новым “бытовым прибором”, таким же привычным, как телефон.

ГЛОНАСС и GPS позволят “присвоить” уникальный адрес буквально каждому квадратному метру поверхности Земли, а это значит, что в ближайшем будущем мы перестанем теряться и метаться в поисках нужного объекта.

Сотни фирм во всем мире оспаривают право на производство НАП СРНС, рынок, который имеет устойчивую тенденцию к увеличению. Следовательно, в мире практически сформировался заказ на НАП СРНС. Поэтому предлагаемый способ соответствует требованию условия “Промышленная применяемость”, П. 19.5.1 “Правил СП-2”.

Стратегия определения орбиты спутников является ключевым вопросом создания любой СРНС. Определение орбиты можно провести наземными измерительными средствами, при этом необходима сеть наземных эталонных станций.

С другой стороны, спутники могли бы автономно вычислять свои координаты с использованием наземных навигационных точек (радиомаяков) или других искусственных спутников Земли. Предложенный способ позволяет производить в беззапросном режиме по доплеровским измерениям путем измерения приращений дальностей с помощью ССН высокоточные траекторные измерения как с использованием сети наземных эталонных комплексов, так и автономно с использованием наземных и других навигационных точек.

Таким образом, предложенный способ определения координат местоположения, составляющих вектора скорости, дальности и траекторных измерений навигирующимся объектом по навигационным радиосигналам космических аппаратов спутниковых радионавигационных систем обладает новизной, существенными отличиями и дает при использовании положительный эффект, заключающийся в повышении точности измерения дальностей, в повышении точности навигационных измерений и определений по навигационному радиосигналу одного НИСЗ, в повышении доступности СРНС и в существенном снижении финансовых затрат на поддержание эксплуатационных характеристик СРНС, а также в повышении точности траекторных измерений в беззапросном режиме с использованием измеренных приращений дальностей и допплеровских сдвигов частоты с помощью ССН.

Литература
1. П. С. Волосов, Ю.С. Дубенко и др. Судовые комплексы спутниковой навигации. – Л.: Судостроение, 1976.

2. В. С. Шебшаевич, П.П. Дмитриев и др. Сетевые спутниковые радионавигационные системы. – М.: Радио и связь. 1993.

3. Корн Г., Корн Т. Справочник по математике. – М.: Наука, 1984.

4. П.Е. Эльясберг. Введение в теорию полета искусственных спутников Земли. – М.: Наука, 1965.

Формула изобретения

1. Способ определения координат местоположения, составляющих вектора скорости, дальности и траекторных измерений навигирующимся объектом по навигационным радиосигналам космических аппаратов спутниковых радионавигационных систем, при котором антенно-приемным устройством, установленным на объекте, принимают навигационные радиосигналы спутников, содержащие в своем составе значения эфемерид, составляющие вектора скорости спутников, а также информацию для введения поправок к частоте и задержке, измеряют дальности от объекта до каждого спутника путем измерения временных сдвигов кодовых последовательностей, формируемых генераторами спутников относительно кодовой последовательности, формируемой генератором объекта с помощью системы слежения за задержкой (ССЗ), а также составляющие вектора скорости объекта путем измерения принимаемых доплеровских сдвигов частоты с помощью системы слежения за несущей (ССН) и определяют координаты местоположения и составляющие вектора скорости объекта, отличающийся тем, что последовательно или параллельно во времени принимают радионавигационные сигналы спутников и по принятым эфемеридным данным вычисляют: проекции N векторов-баз, соединяющих два положения фазовых центров антенн навигационных искусственных спутников Земли (НИСЗ) на орбите, определяемые мерными интервалами, путем вычитания одноименных компонент векторов положения фазовых центров антенн НИСЗ; модули N векторов-баз, как корни квадратные из сумм квадратов проекций векторов-баз на оси выбранной системы координат; значения направляющих косинусов, характеризующие направления векторов-баз в пространстве как отношения соответствующих проекций к значениям модулей векторов-баз; значения косинусов углов между N векторами-базами и векторами, соединяющими вектора положения фазовых центров антенн спутников, находящихся в точках пересечения в серединах векторов-баз, и вектор положения фазового центра антенны навигационной аппаратуры пользователей (НАП) объекта, а также значения их углов как отношения приращений дальностей к значениям модулей векторов-баз и как арки косинусов их отношений; скорости движения НИСЗ по орбите, как отношения произведений осредненных на N-мерных интервалах значений доплеровских сдвигов частоты, длин волн излучаемых навигационных радиосигналов и расстояний между двумя положениями фазовых центров антенн НИСЗ, соответствующих началам и концам N-мерных интервалов к значениям приращений дальностей на мерных интервалах, измеренных с помощью ССН; радиусы орбит НИСЗ, как квадраты отношений, осредненных на мерных интервалах приращений дальностей к произведениям осредненных значений радиальных скоростей, измеренных с помощью ССН на модули векторов-баз, умноженных на коэффициент, равный произведению гравитационной постоянной на массу Земли; периоды орбит НИСЗ как кубы отношений, осредненных на мерных интервалах приращений дальностей к произведениям осредненных радиальных скоростей, измеренных навигационной аппаратурой с помощью ССН, на модули векторов-баз, умноженных на 2 радиан и коэффициент, равный произведению гравитационной постоянной на массу Земли, затем измеряют дальности между фазовым центром антенны НАП объекта и фазовыми центрами антенн спутников, находящихся в точках пересечения векторов-баз, в серединах N векторов-баз с применением измерений временных сдвигов между кодовыми последовательностями, сформированными спутниками и кодовой последовательностью, сформированной в точке приема с помощью ССЗ, каждая из которых синхронизирована по собственному эталону времени, устанавливают систему линейных навигационных уравнений между известными значениями направляющих косинусов векторов-баз и неизвестными значениями направляющих косинусов векторов-дальностей в зависимости от косинусов углов между векторами, как проекции векторов-дальностей на направлении векторов-баз равные сумме произведений их проекций на оси выбранной системы координат, умноженных на соответствующие значения направляющих косинусов векторов-баз, дифференцируют уравнения по времени и с использованием измеренных радиальных скоростей, приращений дальностей, скоростей изменения приращений дальностей с применением ССН определяют координаты местоположения, значения составляющих векторов скорости фазового центра антенны НАП объекта путем решения соответствующих систем уравнений.

2. Способ определения координат местоположения, составляющих вектора скорости, дальности и траекторных измерений по п.1, отличающийся тем, что по эфемернидным данным определяют значения косинусов углов и значения углов между N векторами-базами путем решения уравнений, определяющих функциональные зависимости как косинусы углов между двумя векторами, выраженными через направляющие косинусы векторов-баз и как арки соответствующих косинусов, а также значения углов между векторами-базами и векторами-дальностями, соединяющими вектора положения фазовых центров антенны НИСЗ находящихся в точках пересечения векторов-баз и вектора положения фазового центра антенны НАП объекта, соответствующим определенным мерным интервалам как разности между значениями углов между N векторами-базами и значениями углов между векторами-базами и векторами-дальностями, устанавливают системы линейных навигационных уравнений, дифференцируют уравнения по времени и с применением измеренных радиальных скоростей, приращений дальностей, скоростей изменения приращений дальностей определяют координаты местоположения, значения составляющих вектора скорости фазового центра антенны НАП объекта путем решения соответствующей системы уравнений.

3. Способ определения координат местоположения, составляющих вектора скорости, дальности и траекторных измерений по любому из пп.1 и 2, отличающийся тем, что дальности между фазовым центром антенны НАП объекта навигации и фазовыми центрами антенн НИСЗ, находящихся в точках пересечения векторов-баз измеряют по приращениям фазы несущей навигационных сигналов, соответствующие приращениям дальностей, обусловленных доплеровским сдвигом частоты, путем применения теоремы синусов как отношение значений модулей векторов баз, умноженных на соответствующие значения синусов углов между векторами-базами и векторами-дальностями к значениям синусов сумм также соответствующих углов между векторами-базами и векторами-дальностями.

4. Способ определения координат местоположения, составляющих вектора скорости, дальности и траекторных измерений по любому из пп.1 – 3, отличающийся тем, что в состав эфемерид, рассчитанных по результатам прогнозирования движения спутников для определенных моментов времени, в память спутников закладывают значения модулей и значения направляющих косинусов векторов-баз, определяемые мерными интервалами и размножают их на текущие мерные интервалы.

РИСУНКИ