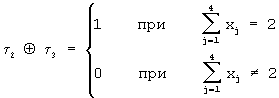Патент на изобретение №2236698
|
||||||||||||||||||||||||||
(54) СПОСОБ ВОСПРОИЗВЕДЕНИЯ СИММЕТРИЧНЫХ БУЛЕВЫХ ФУНКЦИЙ
(57) Реферат:
Изобретение относится к автоматике и вычислительной технике и может быть использовано при построении соответствующих конечных автоматов. Техническим результатом изобретения является упрощение воспроизведения фундаментальных симметричных булевых функций за счет исключения инвертора. Указанный технический результат достигается за счет того, что для воспроизведения фундаментальной симметричной булевой функции индекса m (m Изобретение относится к автоматике и вычислительной технике и может быть использовано при построении соответствующих конечных автоматов. К причине, препятствующей достижению указанного ниже технического результата при использовании известных способов, относится ограниченные функциональные возможности, обусловленные тем, что не воспроизводятся фундаментальные симметричные булевы функции.
К причине, препятствующей достижению указанного ниже технического результата при использовании прототипа, относится то, что для воспроизведения функции Техническим результатом изобретения является упрощение воспроизведения фундаментальных симметричных булевых функций за счет исключения инвертора. Указанный технический результат при осуществлении изобретения достигается тем, что в способе воспроизведения симметричных булевых функций, в котором для воспроизведения фундаментальной симметричной булевой функции индекса m (m Сведения, подтверждающие возможность осуществления изобретения с получением вышеуказанного технического результата, заключаются в следующем. В предлагаемом способе для воспроизведения фундаментальной симметричной булевой функции а значения функций В выражении (1) xil Сначала докажем справедливость (2) при 0& где где где Теперь покажем справедливость (2) при m=0 (m=n). Если m=0 либо m=n, то согласно (1) и (3.3) получим соответственно Пример. Пусть n=4, m=2, тогда согласно (1) получим
В таблице приведены все возможные наборы значений сигналов х1,… ,х4 и соответствующие этим наборам значения функций Таким образом, Вышеизложенные сведения позволяют сделать вывод, что предлагаемый способ обеспечивает воспроизведение фундаментальных симметричных булевых функций без использования инвертора и, следовательно, является по сравнению с прототипом более простым. Формула изобретения
Способ воспроизведения симметричных булевых функций, в котором для воспроизведения фундаментальной симметричной булевой функции индекса m (m MM4A Досрочное прекращение действия патента Российской Федерации на изобретение из-за неуплаты в установленный срок пошлины за поддержание патента в силе
Дата прекращения действия патента: 07.12.2004
Извещение опубликовано: 20.05.2006 БИ: 14/2006
|
||||||||||||||||||||||||||

 {0,…,n}), зависящей от n аргументов – двоичных сигналов, подают указанные сигналы на блок вычисления простых симметричных булевых функций, а значения m-й и (m+1)-й простых симметричных булевых функций суммируют сумматором по модулю 2.
{0,…,n}), зависящей от n аргументов – двоичных сигналов, подают указанные сигналы на блок вычисления простых симметричных булевых функций, а значения m-й и (m+1)-й простых симметричных булевых функций суммируют сумматором по модулю 2.
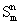 n аргументов – двоичных сигналов указанные сигналы предварительно подают на блок вычисления простых симметричных булевых функций
n аргументов – двоичных сигналов указанные сигналы предварительно подают на блок вычисления простых симметричных булевых функций  0,… ,
0,… , – число (индекс) функции
– число (индекс) функции 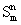 . Как известно,
. Как известно, 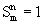 только тогда, когда точно m ее аргументов равны 1, а остальные ее аргументы равны 0.
только тогда, когда точно m ее аргументов равны 1, а остальные ее аргументы равны 0.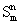 требуются два логических элемента (конъюнктор и инвертор)
требуются два логических элемента (конъюнктор и инвертор) 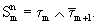 .
.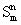 индекса m (m
индекса m (m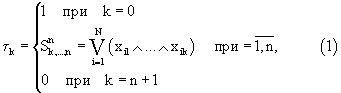
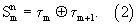
 …
… 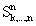 ;
;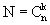 , есть количество неповторяющихся минтермов xi1
, есть количество неповторяющихся минтермов xi1 …
… 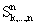 равна 1 только тогда, когда k или больше переменных из х1,… ,хn равны 1, а остальные переменные равны 0.
равна 1 только тогда, когда k или больше переменных из х1,… ,хn равны 1, а остальные переменные равны 0.
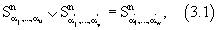
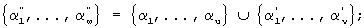
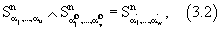
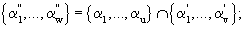
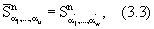
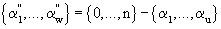 . С учетом (1) и (3.1)-(3.3) можно записать
. С учетом (1) и (3.1)-(3.3) можно записать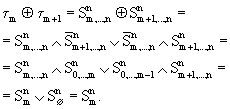
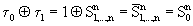 либо
либо 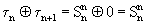 . Справедливость (2) доказана.
. Справедливость (2) доказана. (x1
(x1