Патент на изобретение №2233007

(54) СПОСОБ ПЕРЕДАЧИ ИНФОРМАЦИИ Р-КОДАМИ ФИБОНАЧЧИ ПО МНОГОЛУЧЕВЫМ КАНАЛАМ С РАССЕЯНИЕМ

(57) Реферат:

Изобретение относится к технике радиосвязи и может использоваться в системах последовательной передачи двоичных кодов по каналам с рассеянием и дисперсией. Технический результат предлагаемого способа – выигрыш в скорости передачи информации в 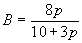раз по сравнению с передачей байта позиционного двоичного кода. Способ передачи информации по многолучевым каналам с рассеянием, заключающийся в том, что передачу осуществляют с использованием р-кода Фибоначчи, в котором параметр р представляет собой целую часть от произведения максимального времени запаздывания распространения сигнала на ширину полосы пропускания канала. 2 ил.

Изобретение относится к технике радиосвязи и может использоваться в системах последовательной передачи двоичных кодов по каналам с рассеянием и дисперсией.

В технике кодирования преобладают позиционные системы отображения информации. Однако во многих случаях выгоднее бывает использовать другие системы счисления. В качестве примера достаточно привести систему остаточных классов (Акушский И.Я., Юдицкий Д.И. Машинная арифметика в остаточных классах. М.: Сов. радио, 1968, 440с.), него-позиционные системы счисления, факториальные, с мнимым основанием и др. (Касаткин В.Н. Новое о системах счисления. Киев: Вища школа, 1982, 92с.). Системы счисления с иррациональным основанием (р-коды Фибоначчи и коды золотой р-пропорции (Стахов А.П. Коды золотой пропорции. М.: Радио и связь, 1984, 152с.)) занимают промежуточное положение между унитарной и позиционной двоичной системой счисления. Особенностями иррациональных систем счисления являются: 1) двоичные, т.е. использующие две цифры – 0 и 1, 2) позиционные системы счисления, сохраняющие все их известные преимущества (простота сравнения чисел по величине, простота арифметических операций, возможность представления чисел с фиксированной и плавающей запятой, однородность и итеративность реализующих арифметику структур и др.); 3) указанные системы обладают избыточностью, которая может использоваться для контроля ошибок при передаче информации и синхронизации) (см. а.с. СССР №№842782, 842786 по классу G 06 F).

Перспективным является использование р-кодов Фибоначчи для увеличения скорости передачи информации по каналам связи. Р-коды Фибоначчи обладают естественной избыточностью (см. книгу Стахова А.П. Коды золотой пропорции. М.: Радио и связь, 1984, 152с.). Избыточность обычно приводит к уменьшению скорости передачи информации (см. Андронов И.С., Финк Л.М. Передача дискретных сообщений по параллельным каналам. М.: Сов. Радио, 408с.). Поэтому для увеличения скорости передачи информации используют различные методы борьбы с избыточностью (см. заявку №2001103038 по классу G 08 C 19/28 “Кодоимпульсное устройство с сокращением избыточности информации”). Скорость передачи информации также ограничена в каналах с многолучевой структурой поля и расплыванием фронтов импульсной посылки за счет дисперсионнных свойств атмосферы.

Искажения длительности импульсов за счет многолучевости появляется в тех случаях, когда длительность импульса _и соизмерима с временем запаздывания t₃ волн, формирующих сигнал. При всех видах манипуляции временные искажения зависят от соотношения фаз и амплитуд волн, формирующих сигнал. Учитывая статистические характеристики ионосферы (или тропосферы для тропосферного рассеяния), можно считать, что сдвиг фаз между отдельными волнами может равновероятно принимать любые значения в пределах от 0 до 360. Корреляция амплитудных флуктуаций менее очевидна (Черенкова Е.Л., Чернышев О.В. Распространение радиоволн. М.: Радио и связь, 1984, 272с.). Однако расчеты показывают, что если амплитуды отдельных волн соизмеримы по среднему значению, то даже при полном отсутствии корреляции между их случайными изменениями вероятность временных искажений остается недопустимо высокой.

Минимальное время запаздывания t₃=t_max в коротковолновых каналах обычно составляет 1,5 мс. Если принять, что исправляющая способность аппаратуры равна 40%, то минимально допустимые длительности должны быть в 2,5 раза больше указанного значения t_max, т.е. составлять 3,75 мс. Для передачи одного байта информации потребуется минимум 30 мс. С другой стороны, для передачи по каналу связи с полосой f_П=30 кГц одного импульса прямоугольной формы достаточно 33 мкс. Поэтому длительность передаваемого импульса оказывается примерно на два порядка больше, чем минимально возможная.

Наиболее близким по технической сущности к предлагаемому является способ, описанный в а.с. СССР №1562948 А1 “Способ последовательной передачи и приема цифровой информации и устройство его осуществления” по классу G 08 C 19/24, Н 03 Н 7/22, опубл. 07.05.90, БИ №17, принятый за прототип.

В способе-прототипе исходную двоичную комбинацию, состоящую из единичных и нулевых импульсов, преобразуют в интервально-импульсную последовательность сигналов таким образом, что единичному и нулевому импульсам исходного сигнала соответствуют временные интервалы между единичными прямоугольными импульсами произвольной длительности T₁, интервально-импульсной последовательности сигналов произвольной длительности Т₂ и Т₃ соответственно, причем Т₃>(0,5T₁+Т₂), восстановление кодовой последовательности единичных и нулевых сигналов осуществляют стробированием принимаемой интервально-импульсной последовательности сигналов в моменты времени, отстоящие от заднего фронта каждого принимаемого прямоугольного импульса интервально-импульсной последовательности на временной интервал, равный (0,5T₁+Т₂) и, если в момент стробирования принимаемая последовательность имеет единичный импульс, то формируют единичный импульсный сигнал исходной кодовой последовательности единичных и нулевых импульсных сигналов, если в момент стробирования принимаемая последовательность имеет нулевой импульс, то формируют нулевой сигнал исходной последовательности двоичного кода.

Способ-прототип, основанный на преобразовании двоичного позиционного кода в интервально-импульсную последовательность, используется для передачи информации по многолучевым каналам с рассеянием.

Отметим, что в случае интервально-импульсной модуляции отсутствует необходимость в синхронизации приемопередающей аппаратуры, а средняя частота стробирования передаваемого сигнала выше, чем при использовании, например, позиционно-импульсной модуляции. При этом между импульсами имеются “пустые” интервалы, которые могут использоваться для компенсации запаздывания t₃ (фиг.1).

Недостатком способа-прототипа является малая скорость передачи информации по многолучевым каналам.

Для обеспечения большей скорости передачи информации по многолучевым каналам предлагается более быстрый способ передачи информации, заключающийся в последовательной передаче с передающей стороны на приемную двоичных сигналов р-кодами Фибоначчи в минимальной форме.

Для устранения указанного недостатка в способе передачи информации по многолучевым каналам с рассеянием, согласно изобретению, передачу осуществляют с использованием p-кода Фибоначчи, в котором параметр р представляет собой целую часть от произведения максимального времени запаздывания распространения сигнала на ширину полосы пропускания канала.

Обозначая через [Х] наибольшее целое число, не превосходящее X, получим:

Полученное в формуле (1) целое число П численно равняется в р-коде Фибоначчи числу р.

Полную длину р-кода Фибоначчи L можно найти по эмпирической формуле, предложенной авторами:

Погрешность последней формулы не превосходит 1 наименьшего разряда представления числа в р-коде Фибоначчи. Выигрыш B в скорости передачи р-кода Фибоначчи по сравнению с одним байтом позиционного двоичного кода определяется по формуле:

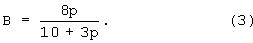Используя формулы (1)-(3), полученные авторами, можно определить параметры передаваемого р-кода и получаемый при этом выигрыш В.

Например, если t_max=3,5 мс, f_П=30 кГц, то, исходя из формулы (1), получим П=р=112. Длина р-кода Фибоначчи при этом будет, согласно формуле (2): L=10+3р=346.

Выигрыш в скорости передачи будет В=2,6. Т.е. в 2,6 раза скорость передачи информации р-кодом Фибоначчи будет выше, чем позиционного двоичного кода, у которых значения t_max одинаковы и равны 3,5 мс.

Как видно из формулы (3), выигрыш при малых значениях р получается меньше, чем при больших. Для p=1 скорость передачи р-кодами Фибоначчи оказывается меньше, чем для позиционного двоичного кода. При р=2 отношение (3) равно единице, т.е. эффективность р-кода Фибоначчи и позиционного двоичного кода одинакова. Для больших значений р получается выигрыш в скорости передачи информации р-кодами Фибоначчи.

Реализовать предложенный способ можно с помощью устройства, приведенного на фиг.2.

Устройство содержит процессор 1 счетно-решающего блока, универсальный регистр 2, соединенный с процессором 1 двунаправленными шинами данных 3 и шинами управления 4, тактовый генератор 5, соединенный с первым входом элемента 6, являющимся логической схемой И, а второй вход элемента 6 соединен с шиной процессора 1, выход элемента 6 соединен с тактовым входом универсального регистра 2, последовательный выход которого соединен с передатчиком 7, а последовательный вход универсального регистра 2 соединен с приемным устройством 8.

Устройство передачи и приема р-кода Фибоначчи (фиг.2) работает следующим образом.

Для передачи р-кода Фибоначчи в процессоре 1 счетно-решающего блока формируется р-код Фибоначчи, который через двунаправленную шину данных 3 записывается в параллельном коде в универсальный регистр 2. В это время на втором входе элемента 6 устанавливается низкий потенциал, запрещающий прохождение импульсов тактового генератора 5 на тактовый вход универсального регистра 2. После записи р-кода Фибоначчи в универсальный регистр 2 потенциал на втором входе элемента 6 становится высоким, а на выходе элемента 6 появляются импульсы, подключаемые к тактовому входу универсального регистра 2. В результате на последовательном выходе универсального регистра 2 формируется импульсная последовательность, соответствующая передаваемому р-коду Фибоначчи. С помощью передатчика 7 указанная последовательность излучается в эфир. После окончания передачи р-кода Фибоначчи на втором входе элемента 6 устанавливается низкий потенциал и универсальный регистр 2 перестает осуществлять сдвиг записанной информации.

Прием р-кода Фибоначчи осуществляется в следующем порядке. Принятый из эфира сигнал в приемном устройстве 8 приобретает форму последовательности импульсов, которые поступают на последовательный вход универсального регистра 2. С началом приема на втором входе элемента 6 потенциал становится высоким, а на выходе элемента 6 появляются импульсы, подаваемые на тактовый вход универсального регистра 2. В результате в универсальном регистре 2 устанавливается принятый р-код Фибоначчи. Затем подается сигнал по шинам управления 4 на переписку кода, установленного в универсальном регистре 2 по адресным шинам 3 в процессор 1. В процессоре 1 р-код Фибоначчи преобразуется в позиционный двоичный код и производятся другие математические операции с принятым кодом.

Помимо передачи двоичной информации по многолучевым каналам с рассеянием, предложенный способ может использоваться в радиолокации.

В прототипе для передачи информации по многолучевым каналам с рассеянием, например, байта исходного позиционного двоичного кода используется 8 позиций, что требует для формирования кода не менее 8t₃ тактовых интервалов.

Предлагаемый способ позволяет значительно увеличить скорость передачи информации, получив выигрыш согласно заявляемой формуле.

Таким образом, предлагается более быстрый способ передачи информации, основанный на применении p-кодов Фибоначчи в минимальной форме.

Формула изобретения

Способ передачи информации по многолучевым каналам с рассеянием, отличающийся тем, что передачу осуществляют с использованием р-кода Фибоначчи, в котором параметр р представляет собой целую часть от произведения максимального времени запаздывания распространения сигнала на ширину полосы пропускания канала.

РИСУНКИ