Патент на изобретение №2228539
|
||||||||||||||||||||||||||
(54) ФУНДАМЕНТАЛЬНЫЙ СИММЕТРИЧНЫЙ МОДУЛЬ
(57) Реферат: Изобретение относится к вычислительной технике и может быть использовано для построения средств автоматики, функциональных узлов систем управления. Техническим результатом является расширение функциональных возможностей за счет обеспечения вычисления фундаментальной симметричной булевой функции 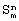 , где m , где m {0,…,n}. Устройство содержит два компаратора, операционный усилитель, логический элемент И, n размыкающих ключей, n+1 резисторов. 1 ил.
Изобретение относится к вычислительной технике и может быть использовано для построения средств автоматики, функциональных узлов систем управления и др.
Известны фундаментальные симметричные модули (см., например, свидетельство РФ 21679, кл. G 06 G 7/25, 2002 г.), которые могут быть использованы для вычисления фундаментальной симметричной булевой функции {0,…,n}. Устройство содержит два компаратора, операционный усилитель, логический элемент И, n размыкающих ключей, n+1 резисторов. 1 ил.
Изобретение относится к вычислительной технике и может быть использовано для построения средств автоматики, функциональных узлов систем управления и др.
Известны фундаментальные симметричные модули (см., например, свидетельство РФ 21679, кл. G 06 G 7/25, 2002 г.), которые могут быть использованы для вычисления фундаментальной симметричной булевой функции 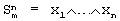 , зависящей от n аргументов – входных двоичных сигналов х1,…,хn , зависящей от n аргументов – входных двоичных сигналов х1,…,хn  {0,l}. Здесь m=n есть заданное {0,l}. Здесь m=n есть заданное  -число (индекс) функции -число (индекс) функции 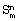 . Как известно, . Как известно, 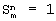 только тогда, когда точно m ее аргументов равны 1, а остальные ее аргументы равны 0.
К причине, препятствующей достижению указанного ниже технического результата при использовании известных фундаментальных симметричных модулей, относится ограниченные функциональные возможности, обусловленные тем, что не выполняется вычисление функции только тогда, когда точно m ее аргументов равны 1, а остальные ее аргументы равны 0.
К причине, препятствующей достижению указанного ниже технического результата при использовании известных фундаментальных симметричных модулей, относится ограниченные функциональные возможности, обусловленные тем, что не выполняется вычисление функции 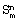 , где m , где m {0,…,n-1}.
Наиболее близким устройством того же назначения к заявленному изобретению по совокупности признаков является принятый за прототип фундаментальный симметричный модуль (свидетельство РФ 20593, кл. G 06 G 7/25, 2001 г.), который содержит два компаратора и n размыкающих ключей и может быть использован для вычисления фундаментальной симметричной булевой функции {0,…,n-1}.
Наиболее близким устройством того же назначения к заявленному изобретению по совокупности признаков является принятый за прототип фундаментальный симметричный модуль (свидетельство РФ 20593, кл. G 06 G 7/25, 2001 г.), который содержит два компаратора и n размыкающих ключей и может быть использован для вычисления фундаментальной симметричной булевой функции 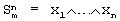 индекса m=n, зависящей от n аргументов – входных двоичных сигналов х1,…,хn индекса m=n, зависящей от n аргументов – входных двоичных сигналов х1,…,хn  {0,1}.
К причине, препятствующей достижению указанного ниже технического результата при использовании прототипа, относятся ограниченные функциональные возможности, обусловленные тем, что не выполняется вычисление функции S {0,1}.
К причине, препятствующей достижению указанного ниже технического результата при использовании прототипа, относятся ограниченные функциональные возможности, обусловленные тем, что не выполняется вычисление функции S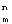 , где m , где m {0,…,n-1}.
Техническим результатом изобретения является расширение функциональных возможностей за счет обеспечения вычисления фундаментальной симметричной булевой функции S {0,…,n-1}.
Техническим результатом изобретения является расширение функциональных возможностей за счет обеспечения вычисления фундаментальной симметричной булевой функции S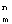 , где m , где m {0,…,n}.
Указанный технический результат при осуществлении изобретения достигается тем, что в фундаментальном симметричном модуле, содержащем два компаратора и n размыкающих ключей, у которых выход каждого предыдущего размыкающего ключа соединен с входом последующего размыкающего ключа, особенность заключается в том, что в него введены операционный усилитель, логический элемент И и n+1 резисторов, причем i-й {0,…,n}.
Указанный технический результат при осуществлении изобретения достигается тем, что в фундаментальном симметричном модуле, содержащем два компаратора и n размыкающих ключей, у которых выход каждого предыдущего размыкающего ключа соединен с входом последующего размыкающего ключа, особенность заключается в том, что в него введены операционный усилитель, логический элемент И и n+1 резисторов, причем i-й 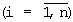 резистор подсоединен между входом и выходом i-го размыкающего ключа, а (n+1)-ый резистор – между входом первого размыкающего ключа и шиной нулевого потенциала, выход первого и выход второго компараторов подключены соответственно к первому и второму входам логического элемента И, подсоединенного выходом к выходу фундаментального симметричного модуля, i-й информационный и первый, второй, третий настроечные входы которого образованы соответственно управляющим входом i-го размыкающего ключа и инвертирующим входом первого, неинвертирующим входом второго компараторов, неинвертирующим входом операционного усилителя, подсоединенного инвертирующим входом и выходом соответственно к входу первого размыкающего ключа и объединенным выходу n-го размыкающего ключа, неинвертирующему входу первого, инвертирующему входу второго компараторов.
На чертеже представлена схема предлагаемого фундаментального симметричного модуля.
Фундаментальный симметричный модуль содержит размыкающие ключи 11,…,1n, резисторы 21,…,2n+1, операционный усилитель 3, компараторы 41 и 42, логический элемент И 5, причем резистор резистор подсоединен между входом и выходом i-го размыкающего ключа, а (n+1)-ый резистор – между входом первого размыкающего ключа и шиной нулевого потенциала, выход первого и выход второго компараторов подключены соответственно к первому и второму входам логического элемента И, подсоединенного выходом к выходу фундаментального симметричного модуля, i-й информационный и первый, второй, третий настроечные входы которого образованы соответственно управляющим входом i-го размыкающего ключа и инвертирующим входом первого, неинвертирующим входом второго компараторов, неинвертирующим входом операционного усилителя, подсоединенного инвертирующим входом и выходом соответственно к входу первого размыкающего ключа и объединенным выходу n-го размыкающего ключа, неинвертирующему входу первого, инвертирующему входу второго компараторов.
На чертеже представлена схема предлагаемого фундаментального симметричного модуля.
Фундаментальный симметричный модуль содержит размыкающие ключи 11,…,1n, резисторы 21,…,2n+1, операционный усилитель 3, компараторы 41 и 42, логический элемент И 5, причем резистор 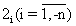 подсоединен между входом и выходом ключа 1i, а резистор 2n+1 – между входом ключа 11 и шиной нулевого потенциала, выход каждого предыдущего ключа соединен с входом последующего ключа, а выходы компараторов 41 и 42 подсоединены соответственно к первому и второму входам элемента 5, подключенного выходом к выходу фундаментального симметричного модуля, i-й информационный и первый, второй, третий настроечные входы которого образованы соответственно управляющим входом ключа 1i и инвертирующим входом компаратора 41, неинвертирующим входом компаратора 42, неинвертирующим входом усилителя 3, подсоединенного инвертирующим входом и выходом соответственно к входу ключа 1 и объединенным выходу ключа 1n, неинвертирующему входу компаратора 41, инвертирующему входу компаратора 42.
Работа предлагаемого фундаментального симметричного модуля осуществляется следующим образом. На его первый,…, n-й информационные входы подаются соответственно двоичные сигналы х1,…,хn подсоединен между входом и выходом ключа 1i, а резистор 2n+1 – между входом ключа 11 и шиной нулевого потенциала, выход каждого предыдущего ключа соединен с входом последующего ключа, а выходы компараторов 41 и 42 подсоединены соответственно к первому и второму входам элемента 5, подключенного выходом к выходу фундаментального симметричного модуля, i-й информационный и первый, второй, третий настроечные входы которого образованы соответственно управляющим входом ключа 1i и инвертирующим входом компаратора 41, неинвертирующим входом компаратора 42, неинвертирующим входом усилителя 3, подсоединенного инвертирующим входом и выходом соответственно к входу ключа 1 и объединенным выходу ключа 1n, неинвертирующему входу компаратора 41, инвертирующему входу компаратора 42.
Работа предлагаемого фундаментального симметричного модуля осуществляется следующим образом. На его первый,…, n-й информационные входы подаются соответственно двоичные сигналы х1,…,хn  {0,1}; на его первом, втором и третьем настроечных входах фиксируются соответственно необходимые управляющие сигналы (напряжения) у1, у2 и у3. Если хi=1 {0,1}; на его первом, втором и третьем настроечных входах фиксируются соответственно необходимые управляющие сигналы (напряжения) у1, у2 и у3. Если хi=1 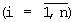 либо хi=0, то ключ 1i соответственно разомкнут либо замкнут. Таким образом, сигналы на выходах компараторов 41 и 42 определяются соответственно выражениями либо хi=0, то ключ 1i соответственно разомкнут либо замкнут. Таким образом, сигналы на выходах компараторов 41 и 42 определяются соответственно выражениями
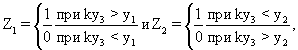 где
где 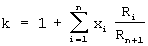 есть коэффициент усиления неинвентирующего усилителя, образованного операционным усилителем 3 и резисторами 21,…,2n+1, сопротивления которых есть R1,…,Rn+1 соответственно. Если r1=…=Rn+1 и уi=у3(mj+0,5), где mj есть коэффициент усиления неинвентирующего усилителя, образованного операционным усилителем 3 и резисторами 21,…,2n+1, сопротивления которых есть R1,…,Rn+1 соответственно. Если r1=…=Rn+1 и уi=у3(mj+0,5), где mj  {0,…, n+1}, j {0,…, n+1}, j {1,2}, то {1,2}, то
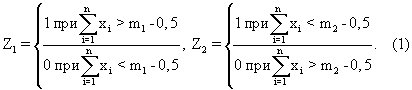 Согласно (1), Z1=1 (Z2=0) при m1
Согласно (1), Z1=1 (Z2=0) при m1 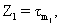 . .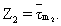 Поскольку сигнал на выходе предлагаемого модуля определяется выражением Z=Z1 Поскольку сигнал на выходе предлагаемого модуля определяется выражением Z=Z1  Z2, получаем Z2, получаем 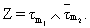 Пусть m1=m, m2=m+1 (m Пусть m1=m, m2=m+1 (m {0,…, n}), тогда {0,…, n}), тогда
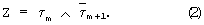 Правая часть равенства (2) совпадает с правой частью равенства
Правая часть равенства (2) совпадает с правой частью равенства 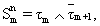 приведенного на стр. 127 в книге Поспелов Д.А. Логические методы анализа и синтеза схем. М.: Энергия, 1974. Следовательно, приведенного на стр. 127 в книге Поспелов Д.А. Логические методы анализа и синтеза схем. М.: Энергия, 1974. Следовательно, 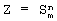 при у1=y3{m+0,5), у2=у3(m+1,5).
Вышеизложенные сведения позволяют сделать вывод, что предлагаемый фундаментальный симметричный модуль обладает более широкими по сравнению с прототипом функциональными возможностями, так как обеспечивает вычисление фундаментальной симметричной булевой функции при у1=y3{m+0,5), у2=у3(m+1,5).
Вышеизложенные сведения позволяют сделать вывод, что предлагаемый фундаментальный симметричный модуль обладает более широкими по сравнению с прототипом функциональными возможностями, так как обеспечивает вычисление фундаментальной симметричной булевой функции 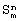 , где m , где m {0,…,n}. {0,…,n}.
Формула изобретения Фундаментальный симметричный модуль, содержащий два компаратора и n размыкающих ключей, у которых выход каждого предыдущего размыкающего ключа соединен с входом последующего размыкающего ключа, отличающийся тем, что в него введены операционный усилитель, логический элемент И и n+1 резисторов, причем i-й 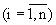 резистор подсоединен между входом и выходом i-го размыкающего ключа, а (n+1)-й резистор – между входом первого размыкающего ключа и шиной нулевого потенциала, выход первого и выход второго компараторов подключены соответственно к первому и второму входам логического элемента И, подсоединенного выходом к выходу фундаментального симметричного модуля, i-й информационный и первый, второй, третий настроечные входы которого образованы соответственно управляющим входом i-го размыкающего ключа и инвертирующим входом первого, неинвертирующим входом второго компараторов, неинвертирующим входом операционного усилителя, подсоединенного инвертирующим входом и выходом соответственно к входу первого размыкающего ключа и объединенным выходу n-го размыкающего ключа, неинвертирующему входу первого, инвертирующему входу второго компараторов. резистор подсоединен между входом и выходом i-го размыкающего ключа, а (n+1)-й резистор – между входом первого размыкающего ключа и шиной нулевого потенциала, выход первого и выход второго компараторов подключены соответственно к первому и второму входам логического элемента И, подсоединенного выходом к выходу фундаментального симметричного модуля, i-й информационный и первый, второй, третий настроечные входы которого образованы соответственно управляющим входом i-го размыкающего ключа и инвертирующим входом первого, неинвертирующим входом второго компараторов, неинвертирующим входом операционного усилителя, подсоединенного инвертирующим входом и выходом соответственно к входу первого размыкающего ключа и объединенным выходу n-го размыкающего ключа, неинвертирующему входу первого, инвертирующему входу второго компараторов.
РИСУНКИ
MM4A Досрочное прекращение действия патента Российской Федерации на изобретение из-за неуплаты в установленный срок пошлины за поддержание патента в силе
Дата прекращения действия патента: 07.12.2004
Извещение опубликовано: 20.05.2006 БИ: 14/2006
|
||||||||||||||||||||||||||
