Патент на изобретение №2227306
|
||||||||||||||||||||||||||
(54) КОМПЕНСАЦИОННЫЙ СПОСОБ ИЗМЕРЕНИЯ РАЗНОСТИ ФАЗ СЛУЧАЙНЫХ СИГНАЛОВ
(57) Реферат: Использование: при обработке радиосигналов, для измерения разности фаз. Технический результат заключается в повышении точности измерения и расширении арсенала действующих способов. С помощью двух синхронно действующих аналого-цифровых преобразователей осуществляют дискретизацию зашумленного Гауссовым аддитивным шумом аналогового случайного сигнала x(t) и его задержанной на время  3 копии y(t)=x(t- 3 копии y(t)=x(t- 3), оценивают разность фаз оптимальным способом и дополнительно по взаимному фазовому спектру, полученному на основе непрерывного вейвлет-преобразования. Окончательно разность фаз между измеряемыми сигналами рассчитывается как среднее арифметическое разностей фаз, полученных оптимальным способом и по взаимному фазовому спектру на основе непрерывного вейвлет-преобразования. 3 ил.
Изобретение относится к области радиотехники, в частности к способам измерения разности фаз случайных сигналов, и может найти применение при обработке радиосигналов.
Известен способ измерения разности фаз, основанный на преобразовании фазы во временной интервал, при котором для извлечения информации о фазе используются временные интервалы между моментами перехода через нулевой уровень сравниваемых сигналов, опубл. в книге: Переход Н.Г. Измерение параметров фазы случайных сигналов. – Томск: Томское отделение издательства “Радио и связь”, 1991, 310 с.: ил. Этот способ можно реализовать с помощью как триггерных преобразователей фазы во временной интервал, так и преобразователей с перекрытием. Как те, так и другие могут быть выполнены по одно- и двух полупериодной схеме. Однако в данном способе используется информация о фазе не всего сигнала, а лишь двух его точек во времени. Поэтому, как отмечено в книге: Переход Н.Г. Измерение параметров фазы случайных сигналов. – Томск: Томское отделение издательства “Радио и связь”, 1991, 310 с.: ил., этот способ имеет такой недостаток, как низкую помехоустойчивость измерения разности фаз. Наличие узкополосных шумов приводит к искажению фазовых характеристик преобразователей, к смещению оценки разности фаз и резкому увеличению дисперсии вблизи точек разрыва фазовой характеристики (триггерных преобразователей). Наличие широкополосных шумов хотя бы в одном из каналов триггерного преобразователя приводит к смещению фазовой характеристики, зависящему от измеряемой разности фаз 3), оценивают разность фаз оптимальным способом и дополнительно по взаимному фазовому спектру, полученному на основе непрерывного вейвлет-преобразования. Окончательно разность фаз между измеряемыми сигналами рассчитывается как среднее арифметическое разностей фаз, полученных оптимальным способом и по взаимному фазовому спектру на основе непрерывного вейвлет-преобразования. 3 ил.
Изобретение относится к области радиотехники, в частности к способам измерения разности фаз случайных сигналов, и может найти применение при обработке радиосигналов.
Известен способ измерения разности фаз, основанный на преобразовании фазы во временной интервал, при котором для извлечения информации о фазе используются временные интервалы между моментами перехода через нулевой уровень сравниваемых сигналов, опубл. в книге: Переход Н.Г. Измерение параметров фазы случайных сигналов. – Томск: Томское отделение издательства “Радио и связь”, 1991, 310 с.: ил. Этот способ можно реализовать с помощью как триггерных преобразователей фазы во временной интервал, так и преобразователей с перекрытием. Как те, так и другие могут быть выполнены по одно- и двух полупериодной схеме. Однако в данном способе используется информация о фазе не всего сигнала, а лишь двух его точек во времени. Поэтому, как отмечено в книге: Переход Н.Г. Измерение параметров фазы случайных сигналов. – Томск: Томское отделение издательства “Радио и связь”, 1991, 310 с.: ил., этот способ имеет такой недостаток, как низкую помехоустойчивость измерения разности фаз. Наличие узкополосных шумов приводит к искажению фазовых характеристик преобразователей, к смещению оценки разности фаз и резкому увеличению дисперсии вблизи точек разрыва фазовой характеристики (триггерных преобразователей). Наличие широкополосных шумов хотя бы в одном из каналов триггерного преобразователя приводит к смещению фазовой характеристики, зависящему от измеряемой разности фаз  .
Известен также корреляционный способ измерения разности фаз, опубл. в книге: Переход Н.Г. Измерение параметров фазы случайных сигналов. – Томск: Томское отделение издательства “Радио и связь”, 1991, 310 с.: ил. Суть способа заключается в следующем.
Пусть имеются опорное гармоническое колебание Uо(t)=Umo·cos .
Известен также корреляционный способ измерения разности фаз, опубл. в книге: Переход Н.Г. Измерение параметров фазы случайных сигналов. – Томск: Томское отделение издательства “Радио и связь”, 1991, 310 с.: ил. Суть способа заключается в следующем.
Пусть имеются опорное гармоническое колебание Uо(t)=Umo·cos оt и стационарный случайный сигнал Uc(t)=Umc·cos оt и стационарный случайный сигнал Uc(t)=Umc·cos ct, у которого амплитуда Umc и частота ct, у которого амплитуда Umc и частота  с постоянны, а начальная фаза с постоянны, а начальная фаза  случайная величина и равномерно распределена в интервале [- случайная величина и равномерно распределена в интервале [- -, -,  ], т.е. имеет плотность вероятностей ], т.е. имеет плотность вероятностей 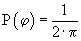 при | при | | |  . Математическое ожидание сигнала Uс(t) равно нулю.
Взаимная корреляционная функция опорного колебания и сигнала определяется выражением . Математическое ожидание сигнала Uс(t) равно нулю.
Взаимная корреляционная функция опорного колебания и сигнала определяется выражением
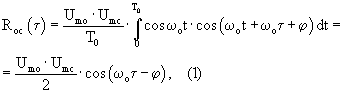 где Т0 – период опорного колебания и сигнала.
Тогда
где Т0 – период опорного колебания и сигнала.
Тогда
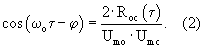 В точках
В точках  о о =(2·n-1)· =(2·n-1)· /2, где n=1-N, отношение /2, где n=1-N, отношение 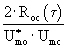 однозначно определяет разность фаз однозначно определяет разность фаз  .
Применяя одно из свойств корреляционной функции, а именно тот факт, что при равенстве аргументов (t1=t2=t) она равна дисперсии Rx(t,t)=Dx(t), а для стационарного случайного процесса Rx(0)=Dx.
При .
Применяя одно из свойств корреляционной функции, а именно тот факт, что при равенстве аргументов (t1=t2=t) она равна дисперсии Rx(t,t)=Dx(t), а для стационарного случайного процесса Rx(0)=Dx.
При  =0 из выражения (1) получим =0 из выражения (1) получим
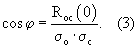 Таким образом, выражения (2) и (3) указывают на принципиальную возможность измерения разности фаз корреляционным способом.
В устройствах, реализующих данный способ, за период Т производится N равномерно распределенных во времени выборок значений исследуемых сигналов с помощью двух синхронно действующих аналого-цифровых преобразователей и на их основе определяется значение cos
Таким образом, выражения (2) и (3) указывают на принципиальную возможность измерения разности фаз корреляционным способом.
В устройствах, реализующих данный способ, за период Т производится N равномерно распределенных во времени выборок значений исследуемых сигналов с помощью двух синхронно действующих аналого-цифровых преобразователей и на их основе определяется значение cos .
Оценка взаимной корреляционной функции при этом равна .
Оценка взаимной корреляционной функции при этом равна
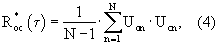 а оценка дисперсий опорного гармонического колебания и стационарного случайного сигнала соответственно
а оценка дисперсий опорного гармонического колебания и стационарного случайного сигнала соответственно
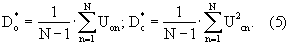 Оценку разности фаз можно получить, подставив выражения (4) и (5) в выражение (3)
Оценку разности фаз можно получить, подставив выражения (4) и (5) в выражение (3)
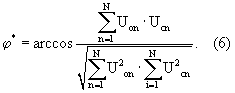 Однако данный способ имеет свои недостатки: как показано в книге: Переход Н.Г. Измерение параметров фазы случайных сигналов. – Томск: Томское отделение издательства “Радио и связь”, 1991, 310 с.: ил., математическое ожидание разности фаз такого корреляционного фазометра имеет смещенную оценку, зависящую от отношения сигнал-шум (ОСШ). Максимальное смещение имеет место при 0 и 180°. К тому же данный метод сложен при реализации измерителя, особенно при цифровой его модификации.
В качестве прототипа выбран оптимальный способ измерения разности фаз, опубл. в книге: Переход Н. Г. Измерение параметров фазы случайных сигналов. – Томск: Томское отделение издательства “Радио и связь”, 1991, 310 с.: ил., а также в книге: Пестряков В.Б. Фазовые радиотехнические системы. – М.: Советское Радио, 1968. – 468 с.
Для неэнергетических параметров, каковым является фаза, алгоритм работы оптимального измерителя фазы определяется из уравнения правдоподобия
Однако данный способ имеет свои недостатки: как показано в книге: Переход Н.Г. Измерение параметров фазы случайных сигналов. – Томск: Томское отделение издательства “Радио и связь”, 1991, 310 с.: ил., математическое ожидание разности фаз такого корреляционного фазометра имеет смещенную оценку, зависящую от отношения сигнал-шум (ОСШ). Максимальное смещение имеет место при 0 и 180°. К тому же данный метод сложен при реализации измерителя, особенно при цифровой его модификации.
В качестве прототипа выбран оптимальный способ измерения разности фаз, опубл. в книге: Переход Н. Г. Измерение параметров фазы случайных сигналов. – Томск: Томское отделение издательства “Радио и связь”, 1991, 310 с.: ил., а также в книге: Пестряков В.Б. Фазовые радиотехнические системы. – М.: Советское Радио, 1968. – 468 с.
Для неэнергетических параметров, каковым является фаза, алгоритм работы оптимального измерителя фазы определяется из уравнения правдоподобия
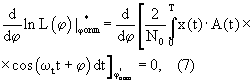 где L(
где L( ) – функция правдоподобия;
S(t, ) – функция правдоподобия;
S(t, )=A(t)·cos( )=A(t)·cos( 0t+ 0t+ ) – сигнал на фоне аддитивного нормального стационарного шума;
Т – период наблюдения сигнала;
N0 – спектральная плотность мощности шума;
x(t) – случайная функция;
A(t) – амплитуда сигнала; ) – сигнал на фоне аддитивного нормального стационарного шума;
Т – период наблюдения сигнала;
N0 – спектральная плотность мощности шума;
x(t) – случайная функция;
A(t) – амплитуда сигнала;
 0 – частота сигнала;
t – время; 0 – частота сигнала;
t – время;
 – фаза сигнала; – фаза сигнала;
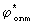 – оптимальная оценка фазы.
Тогда имеем – оптимальная оценка фазы.
Тогда имеем 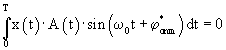 .
Учитывая, что sin( .
Учитывая, что sin( 0t+ 0t+ )=sin )=sin 0t·cos 0t·cos +cos +cos 0t·sin 0t·sin , получим , получим
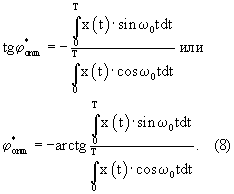 Операции, предписываемые формулой (8), позволяют построить оптимальный измеритель разности фаз случайных сигналов (фиг.1). Принцип работы ясен из фигуры.
Как показано в книге: Пестряков В.Б. Фазовые радиотехнические системы. – М.: Советское Радио, 1968, 468 с., вместо генератора опорного колебания можно использовать генератор копии сигнала или задержанную во времени копию сигнала.
В случае дискретизации зашумленного Гауссовым аддитивным шумом аналогового случайного сигнала x(t) и его задержанной на время
Операции, предписываемые формулой (8), позволяют построить оптимальный измеритель разности фаз случайных сигналов (фиг.1). Принцип работы ясен из фигуры.
Как показано в книге: Пестряков В.Б. Фазовые радиотехнические системы. – М.: Советское Радио, 1968, 468 с., вместо генератора опорного колебания можно использовать генератор копии сигнала или задержанную во времени копию сигнала.
В случае дискретизации зашумленного Гауссовым аддитивным шумом аналогового случайного сигнала x(t) и его задержанной на время  3 копии y(t)=x(t- 3 копии y(t)=x(t- 3), выражение (8) принимает вид 3), выражение (8) принимает вид
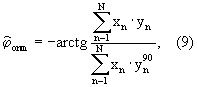 где хn – дискретизированный во времени сигнал x(t);
n=1-N – временной индекс дискретных отсчетов;
N – число дискретных отсчетов;
уn – дискретизированный во времени сигнал y(t);
где хn – дискретизированный во времени сигнал x(t);
n=1-N – временной индекс дискретных отсчетов;
N – число дискретных отсчетов;
уn – дискретизированный во времени сигнал y(t);
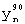 – сигнал yn после фазовращателя на 90 градусов. – сигнал yn после фазовращателя на 90 градусов.
 раз, а для помехи с постоянной амплитудой в два раза.
Целями изобретения являются: повышение точности измерения разности фаз случайных сигналов в условиях аддитивного Гауссова шума и расширение арсенала действующих способов.
Для достижения поставленных целей в компенсационном способе измерения разности фаз случайных сигналов, включающем: дискретизацию зашумленного Гауссовым аддитивным шумом аналогового случайного сигнала x(t) и его задержанной на время раз, а для помехи с постоянной амплитудой в два раза.
Целями изобретения являются: повышение точности измерения разности фаз случайных сигналов в условиях аддитивного Гауссова шума и расширение арсенала действующих способов.
Для достижения поставленных целей в компенсационном способе измерения разности фаз случайных сигналов, включающем: дискретизацию зашумленного Гауссовым аддитивным шумом аналогового случайного сигнала x(t) и его задержанной на время  3 копии y(t)=x(t- 3 копии y(t)=x(t- 3); оценку разности фаз оптимальным способом в соответствии с выражением 9; оценку разности фаз сигналов по взаимному фазовому спектру, рассчитанному на основе непрерывного вейвлет-преобразования, в соответствии с выражением 3); оценку разности фаз оптимальным способом в соответствии с выражением 9; оценку разности фаз сигналов по взаимному фазовому спектру, рассчитанному на основе непрерывного вейвлет-преобразования, в соответствии с выражением
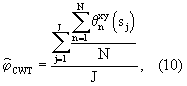 где
где 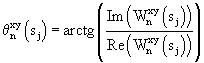 – аргумент взаимного фазового спектра на j-м масштабе; – аргумент взаимного фазового спектра на j-м масштабе;
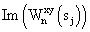 – мнимая часть взаимного фазового спектра; – мнимая часть взаимного фазового спектра;
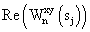 – действительная часть взаимного фазового спектра;
J – число масштабов,
искомую разность фаз сигналов определяют как среднее арифметическое между значениями разности фаз, полученных при их оценке оптимальным способом и по взаимному фазовому спектру на основе непрерывного вейвлет-преобразования.
Общим с прототипом является то, что в предлагаемом способе на одном из этапов вычислений используются результаты оценки разности фаз оптимальным способом. Отличительными признаками предлагаемого способа является то, что на следующем этапе оценивается разность фаз по взаимному фазовому спектру, полученному на основе непрерывного вейвлет-преобразования (CWT, Continuous Wavelet Transform) дискретизированных отсчетов сигналов, опубл. в книге: Новиков Л.В. Основы вейвлет-анализа сигналов. Учебное пособие. Санкт-Петербург: OOO “МОДУС+”, 1999, 152 с.: ил. И окончательно разность фаз между измеряемыми сигналами рассчитывается как среднее арифметическое разностей фаз, полученных оптимальным способом и по взаимному фазовому спектру на основе непрерывного вейвлет-преобразования.
Благодаря новой указанной совокупности существенных признаков технический результат проявляется в повышении в 2-4 раза точности измерения разности фаз в условиях воздействия аддитивного Гауссова шума за счет совместного применения оптимального способа измерения разности фаз и способа на основе непрерывного вейвлет-преобразования, так как смещение оценки разности фаз, рассчитанное как разность между измеренным значением разности фаз – действительная часть взаимного фазового спектра;
J – число масштабов,
искомую разность фаз сигналов определяют как среднее арифметическое между значениями разности фаз, полученных при их оценке оптимальным способом и по взаимному фазовому спектру на основе непрерывного вейвлет-преобразования.
Общим с прототипом является то, что в предлагаемом способе на одном из этапов вычислений используются результаты оценки разности фаз оптимальным способом. Отличительными признаками предлагаемого способа является то, что на следующем этапе оценивается разность фаз по взаимному фазовому спектру, полученному на основе непрерывного вейвлет-преобразования (CWT, Continuous Wavelet Transform) дискретизированных отсчетов сигналов, опубл. в книге: Новиков Л.В. Основы вейвлет-анализа сигналов. Учебное пособие. Санкт-Петербург: OOO “МОДУС+”, 1999, 152 с.: ил. И окончательно разность фаз между измеряемыми сигналами рассчитывается как среднее арифметическое разностей фаз, полученных оптимальным способом и по взаимному фазовому спектру на основе непрерывного вейвлет-преобразования.
Благодаря новой указанной совокупности существенных признаков технический результат проявляется в повышении в 2-4 раза точности измерения разности фаз в условиях воздействия аддитивного Гауссова шума за счет совместного применения оптимального способа измерения разности фаз и способа на основе непрерывного вейвлет-преобразования, так как смещение оценки разности фаз, рассчитанное как разность между измеренным значением разности фаз  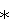 и истинным ее значением и истинным ее значением  ucm ucm 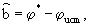 определяемое этими способами, имеет противоположные знаки. Этот эффект особенно заметен при низких отношениях сигнал-шум (менее минус 10 дБ).
Способ осуществляется следующим образом.
Пусть необходимо измерить разность фаз между двумя непрерывными сигналами x(t) и y(t), зашумленными Гауссовым аддитивным шумом. Сигнал y(t) является задержанной на время определяемое этими способами, имеет противоположные знаки. Этот эффект особенно заметен при низких отношениях сигнал-шум (менее минус 10 дБ).
Способ осуществляется следующим образом.
Пусть необходимо измерить разность фаз между двумя непрерывными сигналами x(t) и y(t), зашумленными Гауссовым аддитивным шумом. Сигнал y(t) является задержанной на время  3 копией сигнала x(t), т.е. y(t) = x(t- 3 копией сигнала x(t), т.е. y(t) = x(t- 3).
1. С помощью двух синхронно действующих аналого-цифровых преобразователей за период Т произвести N равномерно распределенных во времени выборок значений исследуемых сигналов. В результате получится по N дискретных отсчетов каждого сигнала.
2. Оценить разность фаз оптимальным способом, определяемым выражением (9).
3. Оценить разность фаз по взаимному фазовому спектру на основе непрерывного вейвлет-преобразования, для чего:
3.1. Задать минимальный масштаб. Например, 3).
1. С помощью двух синхронно действующих аналого-цифровых преобразователей за период Т произвести N равномерно распределенных во времени выборок значений исследуемых сигналов. В результате получится по N дискретных отсчетов каждого сигнала.
2. Оценить разность фаз оптимальным способом, определяемым выражением (9).
3. Оценить разность фаз по взаимному фазовому спектру на основе непрерывного вейвлет-преобразования, для чего:
3.1. Задать минимальный масштаб. Например,
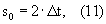 где
где  t – период дискретизации сигнала.
3.2. Задать расстояние между масштабами. Например t – период дискретизации сигнала.
3.2. Задать расстояние между масштабами. Например
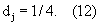 3.3. Вычислить максимальное число масштабов
3.3. Вычислить максимальное число масштабов
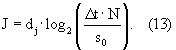 3.4. Вычислить массив частот для дискретного преобразования Фурье
3.4. Вычислить массив частот для дискретного преобразования Фурье
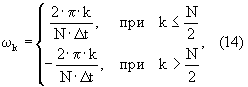 где k=1
где k=1 N – частотный индекс дискретных отсчетов.
3.5. Рассчитать массив масштабов N – частотный индекс дискретных отсчетов.
3.5. Рассчитать массив масштабов
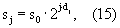 3.6. Вычислить дискретное Фурье-преобразование анализируемого сигнала
3.6. Вычислить дискретное Фурье-преобразование анализируемого сигнала
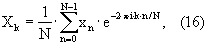 где хn – дискретизированный во времени сигнал x(t);
N – число дискретных отсчетов;
n=1
где хn – дискретизированный во времени сигнал x(t);
N – число дискретных отсчетов;
n=1 N – временной индекс дискретных отсчетов;
k=1 N – временной индекс дискретных отсчетов;
k=1 n – частотный индекс дискретных отсчетов;
i – мнимая единица.
3.7. Выбрать комплекснозначную вейвлет-функцию (базисную вейвлет-функцию). Например, вейвлет Морле (Morlet) имеет вид n – частотный индекс дискретных отсчетов;
i – мнимая единица.
3.7. Выбрать комплекснозначную вейвлет-функцию (базисную вейвлет-функцию). Например, вейвлет Морле (Morlet) имеет вид
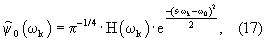 где
где 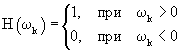 – функция Хевисайда; – функция Хевисайда;
 0 – доминантная частота, позволяющая варьировать избирательностью вейвлета.
3.8. Чтобы гарантировать, что базисная функция имеет единичную энергию, вычислить нормализованную вейвлет-функцию 0 – доминантная частота, позволяющая варьировать избирательностью вейвлета.
3.8. Чтобы гарантировать, что базисная функция имеет единичную энергию, вычислить нормализованную вейвлет-функцию
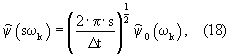 где
где 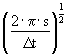 – нормализующий фактор; – нормализующий фактор;
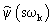 – базисная вейвлет-функция.
3.9. Рассчитать коэффициент, связывающий Фурье-период сигнала и масштаб. Для каждой базисной вейвлет-функции рассчитывается свой коэффициент. Для вейвлета Морле, например, он определяется по формуле – базисная вейвлет-функция.
3.9. Рассчитать коэффициент, связывающий Фурье-период сигнала и масштаб. Для каждой базисной вейвлет-функции рассчитывается свой коэффициент. Для вейвлета Морле, например, он определяется по формуле
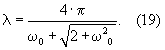 3.10. Вычислить непрерывное вейвлет-преобразование на каждом масштабе
3.10. Вычислить непрерывное вейвлет-преобразование на каждом масштабе
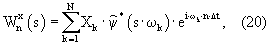 где
где 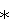 – знак комплексного сопряжения.
3.11. Повторить пп.3.8-3.10 для остальных масштабов.
3.12. Повторить пп.3.6-3.11 для второго сигнала.
3.13. Рассчитать взаимный фазовый спектр анализируемых сигналов на основе полученных вейвлет-коэффициентов первого – знак комплексного сопряжения.
3.11. Повторить пп.3.8-3.10 для остальных масштабов.
3.12. Повторить пп.3.6-3.11 для второго сигнала.
3.13. Рассчитать взаимный фазовый спектр анализируемых сигналов на основе полученных вейвлет-коэффициентов первого 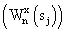 и второго и второго 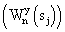 сигналов сигналов
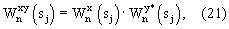 где
где 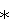 – знак комплексного сопряжения с – знак комплексного сопряжения с 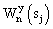 .
В показательной форме выражение примет вид .
В показательной форме выражение примет вид
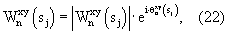 где
где 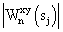 – модуль взаимного фазового спектра; – модуль взаимного фазового спектра;
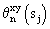 – аргумент взаимного фазового спектра.
3.14. Рассчитать аргумент взаимного фазового спектра на каждом масштабе в дискретные моменты времени – аргумент взаимного фазового спектра.
3.14. Рассчитать аргумент взаимного фазового спектра на каждом масштабе в дискретные моменты времени
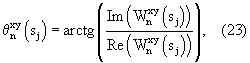 где
где 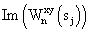 – мнимая часть взаимного фазового спектра; – мнимая часть взаимного фазового спектра;
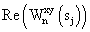 – действительная часть взаимного фазового спектра.
В результате получится масштабно-временная матрица разностей фаз сигналов.
3.15. Определить разность фаз сигналов, как среднее арифметическое масштабно-временной матрицы согласно выражения (10).
4. Вычислить искомую разность фаз сигналов как среднее арифметическое между измеренными в пп.2 и 3 разностями фаз – действительная часть взаимного фазового спектра.
В результате получится масштабно-временная матрица разностей фаз сигналов.
3.15. Определить разность фаз сигналов, как среднее арифметическое масштабно-временной матрицы согласно выражения (10).
4. Вычислить искомую разность фаз сигналов как среднее арифметическое между измеренными в пп.2 и 3 разностями фаз
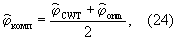 где
где 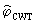 – разность фаз, полученная по взаимному фазовому спектру на основе непрерывного вейвлет-преобразования; – разность фаз, полученная по взаимному фазовому спектру на основе непрерывного вейвлет-преобразования;
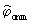 – разность фаз, рассчитанная оптимальным способом.
Для исследования возможности осуществления предложенного способа на ПЭВМ проведено имитационное моделирование измерения разности фаз двух сигналов. Программа написана на языке Matlab. Модель генерирует две реализации одного и того же сигнала, сдвинутых один относительно другого на n3 отсчетов (что является имитацией задержки второго сигнала на – разность фаз, рассчитанная оптимальным способом.
Для исследования возможности осуществления предложенного способа на ПЭВМ проведено имитационное моделирование измерения разности фаз двух сигналов. Программа написана на языке Matlab. Модель генерирует две реализации одного и того же сигнала, сдвинутых один относительно другого на n3 отсчетов (что является имитацией задержки второго сигнала на  3 и, соответственно, сдвига его по фазе) с заданным отношением сигнал-шум 3 и, соответственно, сдвига его по фазе) с заданным отношением сигнал-шум
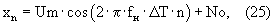 где Um – амплитуда сигнала, В;
fH – несущая частота сигнала, Гц;
где Um – амплитуда сигнала, В;
fH – несущая частота сигнала, Гц;
 T – интервал дискретизации, с;
n=1-N – временной индекс дискретных отсчетов;
N – число дискретных отсчетов;
No – аддитивный Гауссов шум, дБ.
Вторая реализация сигнала получается из первой путем сдвига ее на необходимое число отсчетов T – интервал дискретизации, с;
n=1-N – временной индекс дискретных отсчетов;
N – число дискретных отсчетов;
No – аддитивный Гауссов шум, дБ.
Вторая реализация сигнала получается из первой путем сдвига ее на необходимое число отсчетов
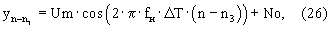 где n3 – число отсчетов задержки сигнала, ед.
В качестве аддитивного шума смоделирован шум, представляющий собой Гауссов случайный процесс. Для непрерывного вейвлет-преобразования в качестве базисной вейвлет-функции брался вейвлет Морле.
Результаты моделирования измерения разности фаз предлагаемым способом приведены на фиг.2, 3. На фиг.2 показана зависимость от отношения сигнал-шум среднеквадратического отклонения (СКО)
где n3 – число отсчетов задержки сигнала, ед.
В качестве аддитивного шума смоделирован шум, представляющий собой Гауссов случайный процесс. Для непрерывного вейвлет-преобразования в качестве базисной вейвлет-функции брался вейвлет Морле.
Результаты моделирования измерения разности фаз предлагаемым способом приведены на фиг.2, 3. На фиг.2 показана зависимость от отношения сигнал-шум среднеквадратического отклонения (СКО)  измерений разности фаз, определяемого, как показано в книге: Дж.Бендат, А.Пирсол. Измерение и анализ случайных процессов. Перевод с английского Г.В.Матушевского и В.Е.Привальского. – М.: Мир, 1974, 464 с., как корень квадратный из дисперсии измерений разности фаз, определяемого, как показано в книге: Дж.Бендат, А.Пирсол. Измерение и анализ случайных процессов. Перевод с английского Г.В.Матушевского и В.Е.Привальского. – М.: Мир, 1974, 464 с., как корень квадратный из дисперсии
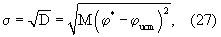 где М – математическое ожидание процесса;
где М – математическое ожидание процесса;
 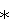 – оценка разности фаз; – оценка разности фаз;
 ист – истинная разность фаз.
На фиг.3 изображена зависимость смещения оценки разности фаз в радианах от отношения сигнал-шум. ист – истинная разность фаз.
На фиг.3 изображена зависимость смещения оценки разности фаз в радианах от отношения сигнал-шум.
Формула изобретения Компенсационный способ измерения разности фаз случайных сигналов, включающий дискретизацию зашумленного Гауссовым аддитивным шумом аналогового случайного сигнала х(t) и его задержанной на время  3 копии y(t)=х(t- 3 копии y(t)=х(t- 3), оценку разности фаз оптимальным способом в соответствии с выражением 3), оценку разности фаз оптимальным способом в соответствии с выражением
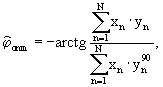 где хn – дискретизированный во времени сигнал x(t);
n=1
где хn – дискретизированный во времени сигнал x(t);
n=1 N – временной индекс дискретных отсчетов;
N – число дискретных отсчетов;
yn – дискретизированный во времени сигнал y(t); N – временной индекс дискретных отсчетов;
N – число дискретных отсчетов;
yn – дискретизированный во времени сигнал y(t);
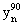 – сигнал уn после фазовращателя на 90 градусов,
отличающийся тем, что дополнительно оценивают разность фаз сигналов по взаимному фазовому спектру, рассчитанному на основе непрерывного вейвлет-преобразования, в соответствии с выражением – сигнал уn после фазовращателя на 90 градусов,
отличающийся тем, что дополнительно оценивают разность фаз сигналов по взаимному фазовому спектру, рассчитанному на основе непрерывного вейвлет-преобразования, в соответствии с выражением
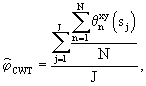 где
где 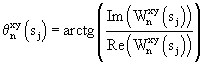 – аргумент взаимного фазового спектра на j-м масштабе; – аргумент взаимного фазового спектра на j-м масштабе;
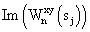 – мнимая часть взаимного фазового спектра; – мнимая часть взаимного фазового спектра;
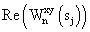 – действительная часть взаимного фазового спектра;
J – число масштабов,
а искомую разность фаз сигналов определяют как среднее арифметическое между значениями разности фаз, полученными при их оценке оптимальным способом и по взаимному фазовому спектру на основе непрерывного вейвлет-преобразования – действительная часть взаимного фазового спектра;
J – число масштабов,
а искомую разность фаз сигналов определяют как среднее арифметическое между значениями разности фаз, полученными при их оценке оптимальным способом и по взаимному фазовому спектру на основе непрерывного вейвлет-преобразования 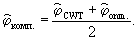
РИСУНКИ
|
||||||||||||||||||||||||||
