Патент на изобретение №2221275

(54) СПОСОБ ИНТЕРПОЛЯЦИИ ДВУХГРАДАЦИОННОГО ИЗОБРАЖЕНИЯ

(57) Реферат:

Изобретение относится к области вычислительной техники и может быть использовано для обработки изображения. Техническим результатом является повышение точности. Изобретение основано на том, что рассчитывают величину интерполяции на основе таблицы пороговых значений в соответствии с контекстом оценки состояния элементов изображения, окружающих интерполируемый элемент изображения, рассчитывают величину интерполяции, рассчитывают контекст изображения, получают пороговое значение, соответствующее рассчитанному контексту и сравнивают величину интерполяции с пороговым значением. 7 з.п.ф-лы, 8 ил.

Настоящее изобретение относится к способу интерполяции двухградационного изображения, а более конкретно к усовершенствованному способу интерполяции, в котором переменное пороговое значение, используемое для определения величины генерируемого посредством интерполяции элемента изображения, определяется на основании контекста (оценки состояния соседних элементов изображения).

Недавно в MPEG-4 была добавлена функция для обработки информации о форме. Информация о форме, которая относится к информации об объекте изображения, называется двухградационным изображением. Для кодирования такого двухградационного изображения в соответствии с MPEG-4 применяется использующий контекст арифметический кодер (САЕ). Для кодирования формы с дефектами к каждому макроблоку двухградационной формы применяется способ нисходящей дискретизации и способ восходящей дискретизации. Изображение формы делится на блоки формы с размером МN.

Нисходящая дискретизация относится к способу уменьшения блока двухградационного изображения в соответствии с заданным коэффициентом преобразования. Уменьшенный блок изображения передается совместно с коэффициентом преобразования. Здесь коэффициент преобразования определяется так, чтобы ошибка между исходным блоком двухградационного изображения и восстановленным позже блоком двухградационного изображения попадала в заранее определенный диапазон.

Полученный нисходящей дискретизацией уменьшенный блок изображения кодируется посредством САЕ и затем передается.

Для восстановления уменьшенного блока изображения используется способ восходящей дискретизации. Восходящая дискретизация используется для восстановления посредством интерполяции из уменьшенного блока изображения блока с размерами исходного блока двухградационного изображения.

Во время такого процесса восходящей дискретизации эффективный способ интерполяции не должен приводить к образованию избыточных блоков и к эффектам избыточного сглаживания в восстановленном двухградационном изображении.

В соответствии с указанным выше требованием целью настоящего изобретения является предоставление усовершенствованного способа интерполяции, в котором для интерполяции используется контекст (оценка состояния опорных элементов изображения, примыкающих к элементу изображения (интерполируемому элементу изображения), генерируемому посредством интерполяции), благодаря чему уменьшается количество блоков и эффект сглаживания.

Для достижения указанной выше цели предоставляется способ интерполяции двухградационного изображения для восстановления блока двухградационного изображения, преобразованного посредством нисходящей дискретизации в блок с размерами блока исходного двухградационного изображения, этот способ состоит из шагов: (а) подготовки таблицы пороговых значений с различными пороговыми значениями в соответствии с контекстом С_р (оценкой состояния) элементов изображения (опорных элементов изображения) уменьшенного изображения, расположенных вокруг интерполирующего элемента изображения; (b) вычисления величины интерполяции на основании величин элементов изображения (элементов изображения объекта), примыкающих к и/или окружающих интерполируемый элемент изображения; (с) вычисления контекста С_р, который является оценкой состояния опорных элементов изображения, окружающих интерполируемый элемент изображения; (d) получения порогового значения, соответствующего вычисленному на основании таблицы пороговых значений контексту; а также (е) сравнения величины интерполяции с пороговым значением, полученным на шаге (d), и установки величины элемента изображения интерполируемого элемента изображения, равной 1, если величина интерполяции превышает пороговое значение, и равной 0, если величина интерполяции меньше или равна пороговому значению.

Предпочтительно, чтобы шаг (а) содержал дополнительные шаги (а1) расчета возможных сумм опорных элементов изображения; (а2) расчета возможных величин интерполяции с учетом возможных сумм опорных элементов изображения; (а3) установки кандидатов пороговых величин с учетом возможных сумм опорных элементов изображения; а также (а4) выбора пороговых значений из множества кандидатов пороговых значений с учетом каждого контекста, соответствующего возможной сумме опорных элементов изображения, приведенного в таблице пороговых значений.

Указанные выше цели и преимущества настоящего изобретения станут более очевидными после детального описания предпочтительных исполнений, представленных ниже со ссылкой на прилагаемые чертежи, на которых:
Фиг.1А является диаграммой, иллюстрирующей способы кодирования и декодирования двухградационного изображения в соответствии с MPEG-4.

Фиг. 1В является макроблоком формы, для которой выполняется шаг нисходящей дискретизации, показанный на фиг.1А.

Фиг. 1С является макроблоком формы, для которой выполняется шаг восходящей дискретизации, показанный на фиг.1А.

Фиг.2 является диаграммой, иллюстрирующей известный способ интерполяции.

Фиг. 3А-3D являются диаграммами, иллюстрирующими способ интерполяции в соответствии с настоящим изобретением.

На фиг.4 показан пример таблицы пороговых значений.

На фиг. 5А представлена таблица, показывающая взаимосвязь между суммой величин опорных элементов изображения и возможных величин интерполяции.

Фиг.5В является таблицей с примерами возможных кандидатов пороговых значений, соответствующих возможным суммам опорных элементов изображения.

Фиг. 6 является таблицей, показывающей медиану, выбранную из множества кандидатов пороговых значений фиг.5В, соответствующих возможным комбинациям контекста.

Фиг.7 является таблицей пороговых значений, заполненной при рассмотрении ограниченного диапазона пороговой величины, показанной на фиг.6 в соответствии с возможными комбинациями контекстов.

Фиг. 8А-8С иллюстрируют результаты выполнения способа интерполяции в соответствии с настоящим изобретением в сравнении с результатами выполнения ранее известного способа.

Способы кодирования и декодирования фиг.1А двухградационного изображения с информацией об объекте в соответствии с MPEG-4 содержат шаг 100 нисходящей дискретизации, шаг кодирования 102, шаг обратного кодирования 104 и шаг восходящей дискретизации 106.

На шаге нисходящей дискретизации 100 МN блок двухградационного изображения преобразуется в (MCR)(NCR) блок двухградационного изображения. Здесь CR является коэффициентом преобразования, указывающим отношение размера уменьшенного блока изображения, полученного нисходящей дискретизацией, к размеру исходного блока двухградационного изображения.

На шаге кодирования 102 кодируется уменьшенное изображение. Для кодирования двухградационного изображения, включающего объекты в соответствии с MPEG-4, применяется использующий контекст арифметический кодер (САЕ). САЕ принят в качестве способа кодирования в проверочной модели MPEG-4 благодаря его простоте и относительно высокой эффективности кодирования.

Уменьшенное изображение, закодированное на шаге кодирования 102, передается по трассе передачи. На шаге обратного кодирования 104 закодированное уменьшенное изображение восстанавливается в уменьшенное изображение. На шаге восходящей дискретизации 106 выполняется интерполяция блока уменьшенного изображения для получения блока с размером исходного двухградационного изображения.

На фиг. 1В показаны детали шага 100 нисходящей дискретизации, проиллюстрированной на фиг.1А. Макроблок двухградационного изображения показан на фиг. 1B, где кружки, обозначенные символом “0”, соответствуют двухградационным элементам изображения. Как видно из рассмотрения кружков фиг.1В, обозначенные символом “0” элементы изображения макроблока преобразуются в элементы изображения, обозначенные символом “X”. Здесь размер макроблока определяется с учетом коэффициента преобразования. Коэффициент преобразования в соответствии с MPEG-4 может равняться 1, 1/2 или 1/4. Такое преобразование, выполненное для всех макроблоков, приводит к уменьшению изображения. На фиг.1В четыре элемента изображения (обозначенные символом “0”) макроблока преобразуются в элемент изображения 201, то есть коэффициент преобразования равен 1/2.

Если на шаге нисходящей дискретизации половина или более этих четырех элементов изображения (обозначенных символом “0”) равна 1, то величина преобразованного элемента (обозначенного символом “X”) становится равной 1. Здесь элементы изображения имеющие величину, равную 1, представляют часть изображения, содержащего объект, а элементы изображения, имеющие величину 0, представляют часть изображения во вне объекта. Макроблок, содержащий как элементы изображения величиной 1, так и элементы изображения величиной 0, является граничным блоком информации об объекте.

На фиг. 1С детально проиллюстрирован шаг 106 восходящей дискретизации, проиллюстрированный на фиг. 1А. На шаге восходящей дискретизации каждый элемент изображения макроблока с размером исходного двухградационного блока восстанавливается посредством интерполяции путем использования элементов изображения уменьшенного блока изображения. На фиг.1С элементы изображения, обозначенные как “X”, представляют элементы изображения блока восстановленной формы, а элементы изображения, обозначенные как “0”, представляют элементы изображения блока уменьшенной формы.

В основном, элементы изображения (обозначенные как “X”) блока восстановленной формы 300 получаются из соседних элементов изображения (обозначенных как “0”) макроблока уменьшенной формы, как показано в кружке 303 фиг.1С.

Например, элементы изображения верхней границы 301 и левой границы 302 указаны как элементы изображения, полученные в результате нисходящей дискретизации, которые принадлежат верхнему макроблоку и левому макроблоку соответственно.

Когда элементы изображения нижней границы и правой границы макроблока 300 относятся к соседним элементам изображения, находящимся за пределами блока 300, то элементы изображения, находящиеся за пределами этого блока, могут быть получены путем увеличения наиболее удаленных от середины элементов изображения, находящихся внутри этого блока, как показано на фиг.1С.

Теперь будет описан известный способ интерполяции со ссылкой на фиг.2.

На фиг. 2 элементы изображения А, В, С, D, Е, F, G, Н, I, J, К и L представляют элементы изображения объекта, которые участвуют в процессе интерполяции, а элементы изображения Р1, Р2, Р3 и Р4 представляют интерполируемые элементы изображения, получаемые в результате интерполяции. Здесь элементы изображения объекта А, В, С, D, Е, F, G, Н, I, J, К и L окружают интерполируемые элементы изображения P1, P2, Р3 и Р4. Кроме этого элементы изображения объекта принадлежат к уменьшенному изображению, в то время как интерполируемые элементы изображения принадлежат к восстановленному двухградационному изображению.

Вначале вычисляется величина интерполяции INP[P] следующим образом:
INP[P1]=rA+s(B+C+D)+t(E+F+G+H+I+J+K+L),
INP[P2]=rB+s(A+C+D)+t(E+F+G+H+I+J+K+L),
INP[P3]=rС+s(A+B+D)+t(E+F+G+H+I+J+K+L),
INP[P4]=rD+s(A+B+C)+t(E+F+G+H+I+J+K+L),
где r, s и t являются весами, которые соответствуют расстоянию от интерполируемого элемента изображения, то есть r является весом элемента изображения объекта, ближайшего к интерполируемому элементу изображения, s является весом следующих, ближайших к интерполируемому элементу изображения элементов изображения объекта, а t является весом элементов изображения объекта, окружающих следующие ближайшие элементы изображения. Кроме этого удовлетворяется условие r>s>t.

Затем сравнивается величина интерполяции INP[P] и пороговое значение THR. Здесь пороговое значение THR устанавливается равным величине, равной половине наибольшей возможной величины интерполяции. Например, если r, s и t равны соответственно 4, 2 и 1, то пороговое значение устанавливается равным 8. Если величина интерполяции INP[P] больше порогового значения THR, то величина элемента изображения интерполируемого элемента изображения становится равной 1. В противном случае величина элемента изображения интерполируемого элемента изображения становится равной 0.

Здесь используется только одна пороговая величина THR, но может использоваться и некоторая совокупность величин интерполяции INP. Так, если величина интерполяции INP[P] и пороговое значение THR близки друг к другу, то неизвестно, правильно ли найдена величина элемента изображения интерполируемого элемента изображения. Соответственно возникают различные явления в виде образования блоков или сглаживания в восстановленном двухградационном изображении.

Для уменьшения эффекта образования блоков или сглаживания пороговое значение, которое сравнивается с величиной интерполяции INP[P], определяется адаптивно в соответствии с контекстом (оценкой состояния элементов изображения (опорных элементов изображения), которые окружают интерполируемый элемент изображения), тем самым устраняется неоднозначность при определении величины элемента изображения интерполируемого элемента изображения.

Теперь будет описан способ интерполяции в соответствии с предпочтительным исполнением настоящего изобретения со ссылкой на фиг.3А-3D. На фиг. 3А-3D элементы изображения А, В, С, D, Е, F, G, H, I, J, К и L, обозначенные как “0”, представляют элементы изображения объекта, принадлежащие уменьшенному изображению, элементы изображения Е, F, G, H, I, J, К и L представляют опорные элементы изображения, а элементы изображения Р1, Р2, Р3 и Р4, обозначенные как “X”, представляют интерполируемые элементы изображения, восстановленного двухградационного изображения.

Вначале рассчитывается величина интерполяции INP[P] на основании элементов изображения объекта следующим образом:
INP[P1]=rА+s(B+C+D)+t(E+F+G+H+I+J+K+L),
INP[P2]=rB+s(A+C+D)+t(E+F+G+H+I+J+K+L),
INP[P3]=rC+s(A+B+D)+t(E+F+G+H+I+J+K+L),
IMP[P4]=rD+s(A+B+C)+t(E+F+G+H+I+J+K+L),
где r, s и t являются весами, соответствующими расстоянию от интерполируемого элемента изображения, то есть r является весом элемента изображения объекта, ближайшего к интерполируемому элементу изображения, s является весом следующих ближайших к интерполируемому элементу изображения элементов изображения объекта, a t является весом элементов изображения объекта, окружающих следующие ближайшие элементы изображения. Кроме этого удовлетворяется условие r>s>t. Здесь r, s и t равны соответственно 4, 2 и 1.

Затем на основании следующего уравнения (1) рассчитывается контекст С_р, представляющий собой оценку состояния опорных элементов изображения: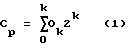

где Р представляет положение интерполируемого элемента изображения, О представляет опорный элемент изображения, a k является индексом опорных элементов изображения, а также весом. Здесь индекс k изменяется в зависимости от взаимного расположения интерполируемого элемента изображения и примыкающих элементов изображения объекта. На фиг.3А-3D показан индекс опорных элементов изображения во время интерполяции интерполируемых элементов изображения P1, Р2, Р3 и Р4.

Затем в соответствии с рассчитанным контекстом на основании таблицы фиг. 4 определяется пороговая величина THR. Пороговая величина фиг.4 получается экспериментальным путем, в результате сравнения исходного изображения и восстановленного двухградационного изображения так, чтобы минимизировать ошибку восстановления.

В таблице пороговых значений фиг.4 величины контекста упорядочиваются в левом столбце по их размерам и по 16 единиц, а в каждой строке упорядочиваются пороговые значения, соответствующие каждой величине контекста.

Так как количество опорных элементов изображения для расчета контекста равно 8, то количество возможных комбинаций оказывается равным 256.

В соответствии с фиг.3А, если величина контекста равна 0, то величина опорных элементов изображения “FELKJIHG” оказывается равной 00000000. Кроме того, величина опорных элементов изображения оказывается равной 10000000 и 01000000, если величины опорных элементов изображения соответственно равны 1 и 2. Кроме этого, если величина контекста равна 255, то величина опорных элементов изображения оказывается равной 11111111.

На фиг.4 ссылочные позиции 400, 402 и 404 представляют пороговые значения, когда величины контекста равны 0, 1 и 2 соответственно. Кроме этого, ссылочная позиция 406 представляет пороговое значение, когда величины контекста равны 255. То есть когда величины контекста равны 0, 1 и 2, то пороговые значения равны 5, 6 и 6 соответственно. Кроме того, когда величина контекста равна 255, то пороговое значение равно 14, как указано ссылочной позицией 406.

Величина интерполяции INP[P] сравнивается с пороговым значением в соответствии с контекстом элементов изображения объекта для определения величины элемента изображения интерполируемого элемента изображения.

Если величина интерполяции INP[P] превышает пороговое значение THR, то величина элемента изображения интерполируемого элемента изображения устанавливается равной 1. В противном случае, величина элемента изображения интерполируемого элемента изображения устанавливается равной 0.

Таблица пороговых величин, используемая в настоящем изобретении, успешно определяется с учетом величин опорных элементов изображения. Процедура подготовки таблицы пороговых значений с учетом величин опорных элементов изображения будет описана со ссылкой на фиг.5-7.

1) Рассчитываются возможные суммы опорных элементов изображения.

Здесь сумма опорных элементов изображения представляет сумму величин элементов изображения опорных элементов изображения, которые учитываются при расчете контекста. Например, она относиться к сумме величин элементов изображения опорных элементов изображения, обозначенных как Е, F, G, Н, I, J, К и L на фиг.3.

Так как на фиг.3 количество опорных элементов изображения равно 8, то возможная сумма опорных элементов изображения равна одному из следующих значений 0, 1, 2, 3, 4, 5, 6, 7 и 8.

2) Рассчитываются возможные величины интерполяции с учетом возможных сумм опорных элементов изображения.

На фиг. 5А показана взаимосвязь между суммами опорных элементов изображения и возможными величинами интерполяции. На фиг.5А суммы опорных элементов изображения упорядочиваются в левом столбце в соответствии с их размером, а возможные величины интерполяции в суммах опорных элементов изображения упорядочиваются в правом столбце. Здесь веса r, s и t равны соответственно 4, 2 и 1.

Например, если сумма опорных элементов изображения равна 0, то есть все величины элементов изображения опорных элементов изображения равны 0, то величина интерполяции равна одному из значений 0, 2, 4, 6, 8 и 10. Если все величины элементов изображения смежных элементов изображения объекта А, В, С и D равны 0, то величина интерполяции становиться равной 0. Кроме того, если все величины элементов изображения смежных элементов изображения объекта А, В, С и D равны 1, то величина интерполяции становится равной 10.

Аналогично, если сумма опорных элементов изображения равна 8, то есть если все величины элементов изображения опорных элементов изображения равны 0, то величина интерполяции становиться равной одному из значений 8, 10, 12, 14, 16 и 18.

3) Определяются возможные кандидаты пороговых значений с учетом возможных сумм опорных элементов изображения.

На фиг. 5В показаны возможные пороговые значения, соответствующие возможным величинам интерполяции. На фиг.5В возможные кандидаты пороговых значений являются медианными величинами каждой смежной пары возможных пороговых величин, упорядоченных по размеру на фиг.5В.

4) Из возможных кандидатов пороговых значений выбирается пороговое значение с учетом соответствующего значения контекста, соответствующего возможным суммам опорных элементов изображения. Здесь пороговое значение может быть медианой возможных пороговых значений.

5) Составляется таблица после приведения в соответствие контекстов выбранным пороговым значениям. Здесь каждый контекст соответствует пороговому значению по отношению к сумме соответствующих опорных элементов изображения.

На фиг.6 показаны пороговые значения, выбранные из кандидатов пороговых значений фиг. 5В, соответствующих величинам, расположенным на медиане кандидатов пороговых значений в соответствии с возможными комбинациями контекста.

На фиг. 6 ссылочные позиции 600, 602 и 604 представляют пороговые значения, когда пороговые значения равны соответственно 0, 1 и 2. Кроме этого, ссылочная позиция 606 представляет пороговое значение, когда величина контекста равна 255. То есть если величины контекста равны 0, 1 и 2, то пороговые значения становятся равными 5, 6 и 6 соответственно. Кроме того, если величин контекста равна 255, то пороговое значение становится равным 13.

Если величина контекста равна 0, то есть если сумма опорных элементов изображения равна 0 на фиг.5А, то множество кандидатов пороговых величин включает -1, 1, 3, 5, 7. 9 и 11, как показано на фиг.5В, и в качестве порогового значения выбирается их медиана, т.е. 5.

Если величина контекста равна 1, то есть если сумма опорных элементов изображения равна 1 на фиг.5А, то множество кандидатов пороговых значений включает 0, 2, 4, 6, 8, 10 и 12, как показано на фиг.5В, а в качестве порогового значения выбирается их медиана, т.е. 6.

Если величина контекста равна 2, то есть если сумма опорных элементов изображения равна 2 на фиг.5А, то множество кандидатов пороговых значений включает 1, 4, 5, 7, 9, 11 и 13, как показано на фиг.5В, и в качестве порогового значения выбирается их медиана, т.е. 7.

Если величина контекста равна 255, то есть если сумма опорных элементов изображения равна 8 на фиг.5А, то множество кандидатов пороговых значений включает 7, 9, 11, 13, 15, 17 и 19, как показано на фиг.5В, а в качестве порогового значения выбирается их медиана, т.е. 13.

Кроме этого на фиг.7 показана таблица пороговых значений, которая заполняется при рассмотрении в качестве диапазона изменения пороговой величины фиг. 6 диапазона 2. То есть пороговые значения из диапазона 2 используются в фактическом двухградационном изображении и затем выбирается пороговое значение, соответствующее наименьшей ошибке воспроизведения.

В способе интерполяции настоящего изобретения неоднозначность результата сравнения величины интерполяции и порогового значения устраняется путем использования оценки состояния (контекста) опорных элементов изображения, окружающих интерполируемый элемент изображения, тем самым ослабляются явления образования блоков и сглаживания в восстановленном двухградационном изображении.

На фиг. 8А-8С сравнивается результат выполнения способа интерполяции в соответствии с настоящим изобретением с результатом выполнения известного способа. Более подробно, на фиг.8А показано исходное двухградационное изображение, на фиг.8В показан результат выполнения ранее известного способа билинейной интерполяции, а на фиг.8С показан результат выполнения интерполяции в соответствии с настоящим изобретением.

Как можно видеть из фиг.8В и 8С, существенно уменьшается эффект образования блоков по сравнению с ранее известным способом билинейной интерполяции.

Как указано выше, в способе интерполяции настоящего изобретения уменьшается неоднозначность при сравнении величины интерполяции и порогового значения путем использования оценки состояния (контекста) опорных элементов изображения, окружающих интерполируемый элемент изображения, тем самым ослабляется явление образования блоков и сглаживание в восстановленном двухградационном изображении.

Так как в способе интерполяции настоящего изобретения переменные пороговые значения, соответствующие комбинации контекста, быстро получаются из таблицы пороговых значений, то и интерполяция может выполняться быстро.

Формула изобретения

1. Способ интерполяции двухградационного изображения для восстановления блока двухградационного изображения, преобразованного посредством нисходящей дискретизации в блок с размером исходного блока двухградационного изображения, при котором получают блоки из двухградационного изображения, преобразуют полученные блоки с учетом коэффициента преобразования в элементы изображения, устанавливают элементы изображения и опорные элементы изображения, на основе которых представляют положение интерполируемого изображения, отличающийся тем, что этот способ содержит шаги, на которых (а) подготавливают таблицу пороговых значений, содержащую различные пороговые значения в соответствии с контекстом С_Р (оценкой состояния) элементов изображения (опорных элементов изображения) уменьшенного изображения вокруг интерполируемого элемента изображения; (b) рассчитывают величину интерполяции на основе значений элементов изображения (элементов изображения объекта), примыкающих и/или окружающих интерполируемый элемент изображения; (с) рассчитывают контекст С_Р, который является оценкой состояния опорных элементов изображения, окружающих интерполируемый элемент изображения; (d) получают пороговое значение, соответствующее вычисленному на основании таблицы пороговых значений контексту; (е) сравнивают величину интерполяции с пороговым значением, полученным на шаге (d), а также устанавливают значение элемента изображения интерполируемого элемента изображения равным 1, если величина интерполяции превышает пороговое значение, и устанавливают значение элемента изображения интерполируемого элемента изображения равным 0, если величина интерполяции меньше или равна пороговому значению, и восстанавливают исходное двухградационное изображение.

2. Способ интерполяции по п.1, отличающийся тем, что на шаге (b) расчет осуществляют посредством способа интерполяции путем использования следующих уравнений:

INP[P1]=rА+s(B+C+D)+t(E+F+G+H+I+J+K+L)

INP[P2]=rB+s(A+C+D)+t(E+F+G+H+I+J+K+L)

INP[P3]=rC+s(A+B+D)+t(E+F+G+H+I+J+K+L)

INP[P4]=rD+s(A+B+C)+t(E+F+G+H+I+J+K+L)

где P1, P2, Р3 и Р4 представляют интерполируемый элемент изображения;

А, В, С и D являются элементами изображения объекта, примыкающими к интерполируемому элементу изображения;

Е, F, G, H, I, J, К и L являются элементами изображения объекта, которые окружают элементы изображения А, В, С и D;

INP[P] представляет величину интерполяции интерполируемого элемента изображения Р;

r является весом элемента изображения объекта, ближайшего к интерполируемому элементу изображения;

s является весом следующих трех ближайших элементов изображения объекта;

a t является весом восьми элементов изображения объекта, окружающих следующие ближайшие элементы изображения, при этом удовлетворяется условие r>s>t.

3. Способ интерполяции по п.1, отличающийся тем, что шаг (с) выполняют путем использования следующего уравнения:

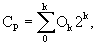где Р представляет положение интерполируемого элемента изображения;

О представляет опорный элемент изображения;

k является индексом опорных элементов изображения.

4. Способ интерполяции по п.3, отличающийся тем, что индекс k на шаге (с) изменяется в соответствии с расположением интерполируемых элементов изображения по отношению к примыкающим элементам изображения.

5. Способ интерполяции по п.1, отличающийся тем, что шаг (а) содержит дополнительные шаги, на которых (а1) рассчитывают возможные суммы опорных элементов изображения, (а2) рассчитывают возможные величины интерполяции с учетом возможных сумм опорных элементов изображения, (а3) устанавливают возможных кандидатов пороговых значений с учетом возможной суммы опорных элементов изображения, а также (а4) выбирают пороговое значение из кандидатов пороговых значений с учетом каждого контекста, соответствующего возможной сумме опорных элементов изображения, что приводит к построению таблицы пороговых значений.

6. Способ интерполяции по п.5, отличающийся тем, что кандидаты пороговых значений на шаге (а3) являются средними значениями каждой соседней пары возможных пороговых значений, упорядоченных по величине.

7. Способ интерполяции по п.5, отличающийся тем, что на шаге (а4) средние значения из кандидатов пороговых значений с учетом каждого контекста выбирают в качестве порогового значения.

8. Способ интерполяции по п.7, отличающийся тем, что дополнительно содержит шаг согласования пороговых значений таблицы посредством принятия заранее определенного диапазона изменения для выбранных пороговых значений и последующего выбора порогового значения в соответствии с каждым контекстом таким образом, чтобы минимальной оказалась ошибка воспроизведения во время применения пороговых значений для фактического двухградационного изображения.

РИСУНКИ