Патент на изобретение №2150122
|
||||||||||||||||||||||||||
(54) СПОСОБ ОПРЕДЕЛЕНИЯ ДВУМЕРНОГО ПЕЛЕНГА И ЧАСТОТЫ ИСТОЧНИКОВ РАДИОИЗЛУЧЕНИЯ
(57) Реферат: Изобретение относится к радиотехнике и может быть использовано для совмещенного поиска и пеленгования по азимуту и углу места с высокой точностью множества кратковременно работающих передатчиков, одновременно попадающих в текущую полосу приема. Способ основан на прямом двумерном Фурье-преобразовании по времени и пространству ансамбля сигналов, принятых кольцевой решеткой из N антенных элементов. На каждой временной частоте, при фиксированных значениях наведения по углу места, каждую сформированную в результате преобразования пространственную частотную составляющую q раз умножают на Фурье-образ функции наведения, зависящей от частоты, угла места, параметров антенной решетки и азимутального циклического сдвига 2  q/M. Производят q пространственных обратных Фурье-преобразований полученной совокупности скорректированных пространственных частотных составляющих, определяют наличие сигнала и получают оценки азимута и угла места его источника на каждой частоте по квадрату модуля двумерного комплексного углового спектра. Технический результат заключается в повышении точности определения пеленга на источник сигналов, принимаемых кольцевой антенной решеткой с произвольным числом элементов. 1 ил. q/M. Производят q пространственных обратных Фурье-преобразований полученной совокупности скорректированных пространственных частотных составляющих, определяют наличие сигнала и получают оценки азимута и угла места его источника на каждой частоте по квадрату модуля двумерного комплексного углового спектра. Технический результат заключается в повышении точности определения пеленга на источник сигналов, принимаемых кольцевой антенной решеткой с произвольным числом элементов. 1 ил.
Изобретение относится к радиотехнике и может быть использовано для радиоконтроля при решении задачи скрытного определения характеристик (частоты, азимута и угла места) множества кратковременно работающих передатчиков, одновременно попадающих в текущую полосу приема. С появлением и совершенствованием систем связи, локации, опознавания и других, использующих сигналы с низкой вероятностью перехвата, то есть с повышенной временной скрытностью (кратковременные пакетные, со скачкообразным изменением частоты) возникают проблемы, связанные с их поиском и пеленгованием с высокой точностью. Известен способ широкополосной пеленгации /1/, при котором из выходных сигналов каждого элемента антенной решетки выделяются цифровые сигналы, характеризующие спектры принятых сигналов, и для каждой выбранной частоты в полосе приема, используя фазу сигналов, производится прямое вычисление пространственного ряда Фурье, дискретно описывающего угловой спектр мощности на выбранной частоте. После восстановления углового спектра на всех частотах определяется пеленг любого источника, излучающего сигналы на любой из частот в пределах текущей полосы приема. Этот способ из максимально возможной амплитудно-фазовой информации использует только фазу сигнала и обладает низким быстродействием при определении азимутального пеленга. Известен более совершенный способ широкополосной пеленгации /2/, использующий при определении пеленга максимально возможную, амплитудно-фазовую информацию, но также обладающий низким быстродействием при определении азимутального пеленга. Известен более эффективный способ определения азимутального пеленга и частоты сигналов передатчиков /3/, использующий свойства симметрии кольцевой антенной решетки и основанный на быстрой свертке комплексных спектральных сигналов каждого антенного элемента с сигналами эталонного амплитудно-фазового распределения, рассчитанного заранее, и принятый за прототип. Согласно этому способу: 1. Выполняют двумерное Фурье-преобразование ансамбля сигналов xn(i), принятых от источника кольцевой решеткой из N антенных элементов, где n – номер антенного элемента, a i – номер временного отсчета сигнала: по времени – 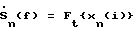 , где Ft {…} – оператор Фурье-преобразования по времени, , где Ft {…} – оператор Фурье-преобразования по времени,по пространству – 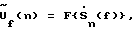 , где F {…} – оператор Фурье-преобразования по пространству на каждой временной частоте f.
2. На каждой частоте f сформированную в результате преобразования пространственную частотную составляющую , где F {…} – оператор Фурье-преобразования по пространству на каждой временной частоте f.
2. На каждой частоте f сформированную в результате преобразования пространственную частотную составляющую 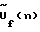 корректируют посредством умножения на корректирующую функцию корректируют посредством умножения на корректирующую функцию 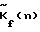 , где , где 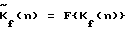 – корректирующая функция или Фурье-образ фазирующей функции (в простейшем случае однолучевого распространения волн – диаграммы направленности решетки на частоте f), имеющей следующий вид – корректирующая функция или Фурье-образ фазирующей функции (в простейшем случае однолучевого распространения волн – диаграммы направленности решетки на частоте f), имеющей следующий вид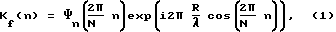 где  n(…) – диаграмма направленности отдельного элемента решетки; n(…) – диаграмма направленности отдельного элемента решетки;n= 0. ..N-1 – текущий номер, a N – число узлов равномерной сетки по азимуту, в которых восстанавливается угловой спектр на частоте f; R – радиус решетки;  – длина волны на частоте f.
3. Выполняют пространственное обратное Фурье-преобразование полученной совокупности скорректированных частотных составляющих для восстановления комплексного углового спектра по азимуту на каждой частоте f по формуле: – длина волны на частоте f.
3. Выполняют пространственное обратное Фурье-преобразование полученной совокупности скорректированных частотных составляющих для восстановления комплексного углового спектра по азимуту на каждой частоте f по формуле: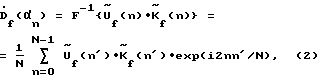 где F-1{…} – оператор обратного Фурье-преобразования по пространству; 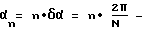 азимутальные направления, по которым на частоте f восстанавливается комплексный угловой спектр азимутальные направления, по которым на частоте f восстанавливается комплексный угловой спектр 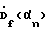 с дискретностью с дискретностью 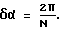 4. Получают оценки азимута источника сигнала на каждой частоте f посредством поиска максимума квадрата модуля комплексного углового спектра 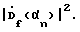 В этом способе, после получения сигналов временного спектра 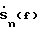 в полосе приема, для восстановления сигналов, описывающих угловой спектр по азимуту на каждой из частот f, вместо требующего большого числа умножений и сложений сигналов, прямого способа выполнения круговой свертки, описываемого формулой в полосе приема, для восстановления сигналов, описывающих угловой спектр по азимуту на каждой из частот f, вместо требующего большого числа умножений и сложений сигналов, прямого способа выполнения круговой свертки, описываемого формулой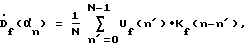 по существу реализован способ быстрого вычисления круговой свертки сигналов с использованием дискретного Фурье-преобразования в соответствии с формулой (2). Способ быстрого вычисления обеспечивает существенное сокращение требуемого количества умножений и сложений сигналов 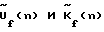 . Он особенно эффективен при реализации с помощью быстрого преобразования Фурье (БПФ).
В свою очередь, особенность БПФ, а следовательно, и свертки (2), такова, что число значений спектра на его выходе равно числу выборок исходного распределения на входе. В данном случае длина последовательностей сигналов . Он особенно эффективен при реализации с помощью быстрого преобразования Фурье (БПФ).
В свою очередь, особенность БПФ, а следовательно, и свертки (2), такова, что число значений спектра на его выходе равно числу выборок исходного распределения на входе. В данном случае длина последовательностей сигналов 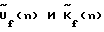 одинакова и равна числу N. При этом угловой спектр по азимуту будет восстановлен с дискретностью 360o/N, а точность пеленгования примерно равна 360o/2N.
Отсюда следует, что для точности пеленгования, равной 0,5o, необходимо иметь в составе антенной решетки 360 антенн. Системы с таким числом антенн являются уникальными и трудно реализуемы.
На практике, как правило, в первую очередь по экономическим соображениям число антенн N изменяется от 5 до 32. В этом случае способом-прототипом, следуя (2), будет восстановлено только от 5 до 32 точек азимутального углового спектра одинакова и равна числу N. При этом угловой спектр по азимуту будет восстановлен с дискретностью 360o/N, а точность пеленгования примерно равна 360o/2N.
Отсюда следует, что для точности пеленгования, равной 0,5o, необходимо иметь в составе антенной решетки 360 антенн. Системы с таким числом антенн являются уникальными и трудно реализуемы.
На практике, как правило, в первую очередь по экономическим соображениям число антенн N изменяется от 5 до 32. В этом случае способом-прототипом, следуя (2), будет восстановлено только от 5 до 32 точек азимутального углового спектра 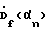 или в других терминах – будет сформирована веерная диаграмма направленности решетки на частоте f, содержащая от 5 до 32 каналов приема. Понятно, что веерная диаграмма с таким числом каналов приема позволяет грубо, с точностью 360o/2N определить угол прихода сигнала по каналу с максимальным уровнем сигнала.
Таким образом, способ-прототип не обеспечивает высокой точности азимутального пеленгования при наиболее часто реализуемых на практике кольцевых конфигурациях антенных решеток с малым числом элементов.
Кроме того, как следует из формулы (1), фазирующая функция способа-прототипа не содержит составляющих, зависящих от угла места. Это означает, что способ-прототип всегда фазирует принимаемые сигналы под нулевым углом места и, следовательно, не обеспечивает измерения угла места источников сигналов.
Как следствие, отсутствие фазирования по углу места дополнительно снижает точность азимутального пеленгования по источникам сигналов с углами места, отличными от нуля. Например, при пеленговании с Земной поверхности источников сигналов, размещаемых на самолетах или спутниках, а также при решении обратной задачи – пеленгования наземного источника с самолета или спутника.
Повышение точности определения угла прихода сигналов, принимаемых кольцевой антенной решеткой с малым числом элементов, при использовании способа-прототипа можно обеспечить несколькими известными путями [4]: или в других терминах – будет сформирована веерная диаграмма направленности решетки на частоте f, содержащая от 5 до 32 каналов приема. Понятно, что веерная диаграмма с таким числом каналов приема позволяет грубо, с точностью 360o/2N определить угол прихода сигнала по каналу с максимальным уровнем сигнала.
Таким образом, способ-прототип не обеспечивает высокой точности азимутального пеленгования при наиболее часто реализуемых на практике кольцевых конфигурациях антенных решеток с малым числом элементов.
Кроме того, как следует из формулы (1), фазирующая функция способа-прототипа не содержит составляющих, зависящих от угла места. Это означает, что способ-прототип всегда фазирует принимаемые сигналы под нулевым углом места и, следовательно, не обеспечивает измерения угла места источников сигналов.
Как следствие, отсутствие фазирования по углу места дополнительно снижает точность азимутального пеленгования по источникам сигналов с углами места, отличными от нуля. Например, при пеленговании с Земной поверхности источников сигналов, размещаемых на самолетах или спутниках, а также при решении обратной задачи – пеленгования наземного источника с самолета или спутника.
Повышение точности определения угла прихода сигналов, принимаемых кольцевой антенной решеткой с малым числом элементов, при использовании способа-прототипа можно обеспечить несколькими известными путями [4]:1. Уточнить грубую оценку угла прихода, сравнивая амплитуды сигналов соседних каналов и применяя методику равносигнального пеленгования. 2. Уточнить грубую оценку угла прихода, применяя в окрестности оцененного максимума аппроксимацию по методу наименьших квадратов двумерным полиномом второго порядка. 3. Дополнить последовательность комплексных сигналов 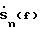 длины N нулями для искусственного увеличения ее длины до М и превращения в последовательность длины N нулями для искусственного увеличения ее длины до М и превращения в последовательность 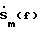 (где m = 0…М – 1 – текущий номер, а М – число узлов равномерной сетки по азимуту, в которых необходимо восстановить угловой спектр на частоте f) и восстановить комплексный угловой спектр по азимуту на каждой частоте f по формуле (2) с заменой индекса n на индекс m.
Первый и второй пути радикально не решают проблему, так как сохраняют зависимость достижимой точности от числа антенн и являются узкополосными при фиксированном числе антенн в решетке.
Третий путь повышения точности пеленгования при использовании способа-прототипа позволяет получить любую требуемую точность пеленгования ценой увеличения числа операций над сигналами, включая и непроизводительные операции. Поэтому он также не приемлем, так как существенно снижает скорость азимутального пеленгования.
Задачей предлагаемого способа является определение с высокой точностью двумерного (по азимуту и углу места) пеленга на источник сигналов, принимаемых кольцевой антенной решеткой с произвольным, в том числе и с малым числом элементов.
Задача решена тем, что в способе определения двумерного пеленга и частоты источников радиоизлучения, основанном на двумерном Фурье-преобразовании (по времени и пространству) ансамбля сигналов, принятых кольцевой решеткой из N антенных элементов, согласно изобретению на каждой временной частоте, при фиксированных значениях наведения по углу места, каждую сформированную в результате преобразования пространственную частотную составляющую q раз умножают на Фурье-образ функции наведения, зависящей от частоты, угла места, параметров антенной решетки и азимутального циклического сдвига 2 (где m = 0…М – 1 – текущий номер, а М – число узлов равномерной сетки по азимуту, в которых необходимо восстановить угловой спектр на частоте f) и восстановить комплексный угловой спектр по азимуту на каждой частоте f по формуле (2) с заменой индекса n на индекс m.
Первый и второй пути радикально не решают проблему, так как сохраняют зависимость достижимой точности от числа антенн и являются узкополосными при фиксированном числе антенн в решетке.
Третий путь повышения точности пеленгования при использовании способа-прототипа позволяет получить любую требуемую точность пеленгования ценой увеличения числа операций над сигналами, включая и непроизводительные операции. Поэтому он также не приемлем, так как существенно снижает скорость азимутального пеленгования.
Задачей предлагаемого способа является определение с высокой точностью двумерного (по азимуту и углу места) пеленга на источник сигналов, принимаемых кольцевой антенной решеткой с произвольным, в том числе и с малым числом элементов.
Задача решена тем, что в способе определения двумерного пеленга и частоты источников радиоизлучения, основанном на двумерном Фурье-преобразовании (по времени и пространству) ансамбля сигналов, принятых кольцевой решеткой из N антенных элементов, согласно изобретению на каждой временной частоте, при фиксированных значениях наведения по углу места, каждую сформированную в результате преобразования пространственную частотную составляющую q раз умножают на Фурье-образ функции наведения, зависящей от частоты, угла места, параметров антенной решетки и азимутального циклического сдвига 2 q/M, производят q пространственных обратных Фурье-преобразований полученной совокупности скорректированных пространственных частотных составляющих, определяют наличие сигнала и получают оценки азимута и угла места его источника на каждой частоте по квадрату модуля двумерного комплексного углового спектра.
На чертеже приведена структурная схема устройства, в котором реализуется предложенный способ.
Согласно предлагаемому способу: q/M, производят q пространственных обратных Фурье-преобразований полученной совокупности скорректированных пространственных частотных составляющих, определяют наличие сигнала и получают оценки азимута и угла места его источника на каждой частоте по квадрату модуля двумерного комплексного углового спектра.
На чертеже приведена структурная схема устройства, в котором реализуется предложенный способ.
Согласно предлагаемому способу:1. Выполняют двумерное Фурье-преобразование ансамбля сигналов xn(i), принятых от источника кольцевой решеткой из N антенных элементов, где n – номер антенного элемента, а i – номер временного отсчета сигнала: по времени – 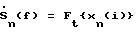 , где Ft{…} – оператор Фурье-преобразования по времени, , где Ft{…} – оператор Фурье-преобразования по времени,по пространству – 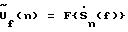 , где F{…} – оператор Фурье-преобразования по пространству на каждой временной частоте f.
2. На каждой временной частоте f, при фиксированном значении угла наведения (фазирования) по углу места h, сформированную в результате преобразования пространственную частотную составляющую , где F{…} – оператор Фурье-преобразования по пространству на каждой временной частоте f.
2. На каждой временной частоте f, при фиксированном значении угла наведения (фазирования) по углу места h, сформированную в результате преобразования пространственную частотную составляющую 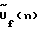 (корректируют q раз посредством умножения на корректирующую функцию (корректируют q раз посредством умножения на корректирующую функцию 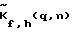 , где , где 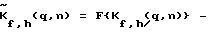 корректирующая функция или Фурье-образ функции наведения на частоте f, имеющей следующий вид: корректирующая функция или Фурье-образ функции наведения на частоте f, имеющей следующий вид: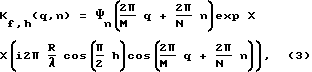 где h= 0. . .H – 1 – текущий номер узла сетки наведения решетки по углу места, а H – число узлов по углу места, в которых восстанавливается срез азимутального углового спектра на частоте f; где q = m(mod(M/N)); m= 0. . . М-1, М – число узлов равномерной сетки по азимуту, в которых восстанавливается угловой спектр на частоте f; n=0…N-1 – номер антенного элемента, N – число антенн в решетке; R – радиус решетки;  – длина волны на частоте f; – длина волны на частоте f; n(…) – диаграмма направленности отдельного элемента решетки.
Из формулы (3) следует, что она является более общей, чем формула (1), и совпадает с ней при следующих значениях индексов q=0 и h=0. Корректирующая функция n(…) – диаграмма направленности отдельного элемента решетки.
Из формулы (3) следует, что она является более общей, чем формула (1), и совпадает с ней при следующих значениях индексов q=0 и h=0. Корректирующая функция 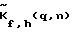 зависит от частоты f, угла места h, параметров антенной решетки зависит от частоты f, угла места h, параметров антенной решетки  n(…), n, N, R и азимутального циклического сдвига 2 n(…), n, N, R и азимутального циклического сдвига 2 q/M . При этом, она позволяет на любой частоте f навести решетку по углу места посредством изменения индекса h и обеспечить эффект циклического вращения решетки в азимутальной плоскости с шагом 2 q/M . При этом, она позволяет на любой частоте f навести решетку по углу места посредством изменения индекса h и обеспечить эффект циклического вращения решетки в азимутальной плоскости с шагом 2 /M при изменении индекса q.
3. Выполняют q пространственных обратных Фурье-преобразований полученной совокупности скорректированных частотных составляющих /M при изменении индекса q.
3. Выполняют q пространственных обратных Фурье-преобразований полученной совокупности скорректированных частотных составляющих 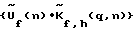 для восстановления М значений комплексного углового спектра на частоте f, при значении наведения по углу места h по формуле: для восстановления М значений комплексного углового спектра на частоте f, при значении наведения по углу места h по формуле: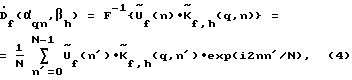 где F-1{…} – оператор обратного Фурье-преобразования по пространству. 4. Повторяют этапы 2 и 3 для всех значений наведения по углу места h = 0…H – 1. 5. Определяют на каждой частоте f квадрат модуля двумерного комплексного углового спектра 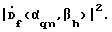 .
6. Используют квадрат модуля .
6. Используют квадрат модуля 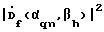 для определения наличия сигнала и получения оценки азимута и угла места его источника на каждой частоте f.
Повышение точности определения двумерного (по азимуту и углу места) пеленга сигналов, принимаемых кольцевой антенной решеткой, достигается за счет восстановления на каждой временной частоте f существенно большего числа значений комплексного углового спектра М, чем число антенн N.
Наиболее важно, что при этом операции умножения на корректирующую функцию могут выполняться как последовательно, так и параллельно во времени. Последнее означает, что предложенный способ может быть реализован как последовательными, так и параллельными устройствами обработки сигналов. При параллельной обработке скорость получения одного азимутального среза диаграммы не отличается от скорости способа-прототипа (2), а точность повышается в М/N раз. Рассмотрим устройство параллельной обработки.
Устройство, реализующее предложенный способ, содержит последовательно соединенные кольцевую антенную решетку 1, N-канальный преобразователь частоты 2, N-канальный аналого-цифровой преобразователь (АЦП) 3, вычислитель двумерного Фурье-преобразования 4, многоканальный параллельный вычислитель 5, устройство вычисления квадрата модуля двумерного комплексного углового спектра для определения наличия сигнала и получения оценки азимута и угла места его источника на каждой частоте f.
Повышение точности определения двумерного (по азимуту и углу места) пеленга сигналов, принимаемых кольцевой антенной решеткой, достигается за счет восстановления на каждой временной частоте f существенно большего числа значений комплексного углового спектра М, чем число антенн N.
Наиболее важно, что при этом операции умножения на корректирующую функцию могут выполняться как последовательно, так и параллельно во времени. Последнее означает, что предложенный способ может быть реализован как последовательными, так и параллельными устройствами обработки сигналов. При параллельной обработке скорость получения одного азимутального среза диаграммы не отличается от скорости способа-прототипа (2), а точность повышается в М/N раз. Рассмотрим устройство параллельной обработки.
Устройство, реализующее предложенный способ, содержит последовательно соединенные кольцевую антенную решетку 1, N-канальный преобразователь частоты 2, N-канальный аналого-цифровой преобразователь (АЦП) 3, вычислитель двумерного Фурье-преобразования 4, многоканальный параллельный вычислитель 5, устройство вычисления квадрата модуля двумерного комплексного углового спектра 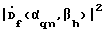 и отображения 6. В свою очередь, вычислитель 5 содержит матрицу вычислителей, элементы которой зависят от двух индексов f = 1…К и h=1…H, где К – число дискрет по временной частоте, а H – число дискрет по углу места. Каждый вычислитель матрицы 5(К, Н) включает запоминающее устройство 7 для хранения заранее вычисленных корректирующих функций и отображения 6. В свою очередь, вычислитель 5 содержит матрицу вычислителей, элементы которой зависят от двух индексов f = 1…К и h=1…H, где К – число дискрет по временной частоте, а H – число дискрет по углу места. Каждый вычислитель матрицы 5(К, Н) включает запоминающее устройство 7 для хранения заранее вычисленных корректирующих функций 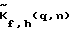 по каждому из сочетаний индексов К и H, а также последовательно подключенные к выходу вычислителя 4, q комплексных умножителей 8(1)… 8(q), q вычислителей одномерного обратного Фурье-преобразования 9(1)…9(q) и устройство накопления 10.
Сигналы, принимаемые антенной решеткой 1, преобразуются на более низкую частоту в преобразователе 2, преобразуются с помощью АЦП 3 в цифровые сигналы xn(i), а в вычислителе 4 находится их двумерный спектр по временной частоте по каждому из сочетаний индексов К и H, а также последовательно подключенные к выходу вычислителя 4, q комплексных умножителей 8(1)… 8(q), q вычислителей одномерного обратного Фурье-преобразования 9(1)…9(q) и устройство накопления 10.
Сигналы, принимаемые антенной решеткой 1, преобразуются на более низкую частоту в преобразователе 2, преобразуются с помощью АЦП 3 в цифровые сигналы xn(i), а в вычислителе 4 находится их двумерный спектр по временной частоте 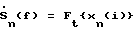 и пространству и пространству 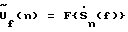 . Если быстродействие АЦП достаточно для непосредственного аналого-цифрового преобразования входных сигналов, как, например, при построении изображения в KB диапазоне, то преобразователь 2 может быть исключен.
В вычислителе 5 восстанавливается двумерный комплексный угловой спектр . Если быстродействие АЦП достаточно для непосредственного аналого-цифрового преобразования входных сигналов, как, например, при построении изображения в KB диапазоне, то преобразователь 2 может быть исключен.
В вычислителе 5 восстанавливается двумерный комплексный угловой спектр 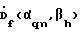 на каждой частоте f, при всех значениях угла наведения по углу места h по формуле (4).
При фиксированных значениях длинны волны или частоты f и угла места h выражение (4) предусматривает выполнение в каждом из умножителей 8(1)…8(q) соответствующего вычислителя 5(К,Н) комплексного умножения сигналов Фурье-образа на каждой частоте f, при всех значениях угла наведения по углу места h по формуле (4).
При фиксированных значениях длинны волны или частоты f и угла места h выражение (4) предусматривает выполнение в каждом из умножителей 8(1)…8(q) соответствующего вычислителя 5(К,Н) комплексного умножения сигналов Фурье-образа 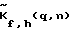 хранящихся в запоминающем устройстве 7, на сигналы Фурье-образа хранящихся в запоминающем устройстве 7, на сигналы Фурье-образа 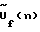 и обратного Фурье-преобразования сигналов полученных произведений и обратного Фурье-преобразования сигналов полученных произведений 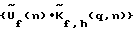 в вычислителях 9(1)…9(q). То есть, сигнал в вычислителях 9(1)…9(q). То есть, сигнал 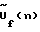 умножается q раз на корректирующую функцию умножается q раз на корректирующую функцию 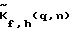 при разных значениях индекса q. Результаты q обратных преобразований, представляющие собой М значений углового спектра в азимутальной плоскости для фиксированной частоты f и фиксированного угла места h, накапливаются в устройстве 10 соответствующего вычислителя 5(К,Н). Все вычислители матрицы 5(К,Н) аналогично одновременно восстанавливают двумерный (по азимуту и углу места) комплексный угловой спектр при разных значениях индекса q. Результаты q обратных преобразований, представляющие собой М значений углового спектра в азимутальной плоскости для фиксированной частоты f и фиксированного угла места h, накапливаются в устройстве 10 соответствующего вычислителя 5(К,Н). Все вычислители матрицы 5(К,Н) аналогично одновременно восстанавливают двумерный (по азимуту и углу места) комплексный угловой спектр 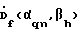 на всех частотах f.
Устройство 6 определяет наличие сигнала и получает оценки азимута и угла места его источника на каждой частоте f по максимумам квадрата модуля двумерного комплексного углового спектра на всех частотах f.
Устройство 6 определяет наличие сигнала и получает оценки азимута и угла места его источника на каждой частоте f по максимумам квадрата модуля двумерного комплексного углового спектра 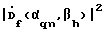 .
Физический смысл предлагаемого способа заключается в следующем. Производится циклическое, q раз, повторение быстрой свертки, длина которой равна числу антенн N с умножением исходных сигналов .
Физический смысл предлагаемого способа заключается в следующем. Производится циклическое, q раз, повторение быстрой свертки, длина которой равна числу антенн N с умножением исходных сигналов 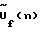 на фазовые множители, зависящие от циклического сдвига 2 на фазовые множители, зависящие от циклического сдвига 2 q/M. Это эквивалентно добавлению к входным сигналам q/M. Это эквивалентно добавлению к входным сигналам 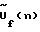 фазы, изменяющейся по закону косинуса (см. формулу (3)), которая вызывает вращение решетки относительно ее фазового центра или вращение ее диаграммы. При этом обеспечивается восстановление на каждой временной частоте f, при фиксированном значении угла места существенно большего числа значений комплексного азимутального углового спектра (диаграммы направленности) М, чем число антенн N, что, в свою очередь, обеспечивает повышение точности в М/N раз. Для наиболее типичных значений М и N, характерных для современных и перспективных пеленгаторов, обеспечивается выигрыш в точности, равный M/N = 512/12 = 42.
Источники информации фазы, изменяющейся по закону косинуса (см. формулу (3)), которая вызывает вращение решетки относительно ее фазового центра или вращение ее диаграммы. При этом обеспечивается восстановление на каждой временной частоте f, при фиксированном значении угла места существенно большего числа значений комплексного азимутального углового спектра (диаграммы направленности) М, чем число антенн N, что, в свою очередь, обеспечивает повышение точности в М/N раз. Для наиболее типичных значений М и N, характерных для современных и перспективных пеленгаторов, обеспечивается выигрыш в точности, равный M/N = 512/12 = 42.
Источники информации1. US, патент, 4 626 859, кл. G 01 S 5/04, 1986 г. 2. RU, патент, 2096797, кл. G 01 S 3/14, 1996 г. 3. US, патент, 4 641 143, кл. G 01 S 5/04, 3/16, G 06 G 7/19, 1987 г. 4. Соломенцев В.В. Быстрая обработка сигналов в ФАР радиопеленгаторов. Теория и практика применения и совершенствования радиоэлектронных систем. МИИГА, 1987. Формула изобретения
 q/M производят q обратных одномерных пространственных в азимутальной плоскости Фурье-преобразований полученной совокупности скорректированных пространственных частотных составляющих, повторяют операции умножения и обратного Фурье-преобразования для всех значений наведения по углу места, определяют наличие сигнала и получают оценки азимута и угла места его источника на каждой частоте по квадрату модуля двумерного комплексного углового спектра. q/M производят q обратных одномерных пространственных в азимутальной плоскости Фурье-преобразований полученной совокупности скорректированных пространственных частотных составляющих, повторяют операции умножения и обратного Фурье-преобразования для всех значений наведения по углу места, определяют наличие сигнала и получают оценки азимута и угла места его источника на каждой частоте по квадрату модуля двумерного комплексного углового спектра.
РИСУНКИ
|
||||||||||||||||||||||||||
