Патент на изобретение №2150098
|
||||||||||||||||||||||||||
(54) СПОСОБ КОНТРОЛЯ ПОТЕРИ УСТОЙЧИВОСТИ МЕТАЛЛИЧЕСКИХ СТРОИТЕЛЬНЫХ КОНСТРУКЦИЙ
(57) Реферат: Изобретение относится к области неразрушающего контроля потери устойчивости металлических строительных конструкций и предназначено для контроля и прогнозирования моментов потери устойчивости несущих металлических строительных конструкций. Сущность способа: определяют критические прогибы и углы закручивания элементов конструкции и упругие характеристики металла, при этом дополнительно определяют критические нагрузки, вызывающие изгибно-крутильную форму потери устойчивости и изгибно-крутильные деформации из системы дифференциальных уравнений устойчивости и из условия Тд  Тф, где Тд, Тф – работа действительных и фиктивных сил на перемещениях при потере устойчивости, вычисляют нагрузку Ркрд и сравнивают ее с предельно возможной нагрузкой Рпред, действующей на конструкцию, и при Ркрд Тф, где Тд, Тф – работа действительных и фиктивных сил на перемещениях при потере устойчивости, вычисляют нагрузку Ркрд и сравнивают ее с предельно возможной нагрузкой Рпред, действующей на конструкцию, и при Ркрд 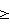 Рпред делают вывод о потере устойчивости конструкции. Изобретение обеспечивает повышение надежности контроля потери устойчивости за счет создания адекватной теоретической модели напряженно-деформированного состояния. 4 ил., 2 табл. Рпред делают вывод о потере устойчивости конструкции. Изобретение обеспечивает повышение надежности контроля потери устойчивости за счет создания адекватной теоретической модели напряженно-деформированного состояния. 4 ил., 2 табл.
Изобретение относится к области неразрушающего контроля потери устойчивости металлических строительных конструкций и предназначено для контроля и прогнозирования момента потери устойчивости несущих металлических строительных конструкций. Известен способ неразрушающего контроля момента потери устойчивости металлических строительных конструкций, изложенный в Строительных нормах и правилах (СНиП II-3-81) [1], опирающийся на труды: В.З. Власов “Тонкостенные упругие стержни”, Москва, 1959 г. Госиздат [2] и С.П. Тимошенко “Устойчивость упругих систем”, Гостехиздат, 1955 г. [3] Упомянутый способ, принятый в качестве ближайшего аналога, включает определение критических прогибов и углов закручивания элементов конструкции и упругих характеристик металла (E, G) с последующим расчетом критических нагрузок и сопоставлением их с предельными значениями нагрузок. Недостаток этого способа – недостаточная достоверность полученных результатов и прогнозов ввиду отсутствия адекватной теоретической модели потери устойчивости. Технический результат изобретения – упрощение и повышение надежности контроля потери устойчивости металлических строительных конструкций за счет создания адекватной теоретической модели напряженно-деформированного состояния при потере устойчивости. Технический результат обеспечивается тем, что способ контроля потери устойчивости металлических строительных стержневых конструкций включает определение критических прогибов и углов закручивания элементов конструкции и упругих характеристик металла (E, G) с последующим расчетом критических нагрузок и сопоставлением их с предельными значениями нагрузок. Дополнительно определяют критические нагрузки Nyф, Nxф, 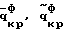 , вызывающие изгибно-крутильную форму потери устойчивости и изгибно-крутильные деформации из системы дифференциальных уравнений устойчивости: , вызывающие изгибно-крутильную форму потери устойчивости и изгибно-крутильные деформации из системы дифференциальных уравнений устойчивости: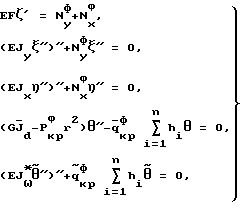 (1) (1)где Jx – момент инерции поперечного сечения элементов конструкции относительно оси OX; Jy – момент инерции площади поперечного сечения элементов конструкции относительно оси OY; 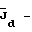 крутильный момент инерции поперечного сечения элементов конструкции при раздельном включении; крутильный момент инерции поперечного сечения элементов конструкции при раздельном включении;J*  – раздельный секторальный момент инерции поперечного сечения элементов конструкции; – раздельный секторальный момент инерции поперечного сечения элементов конструкции;F – площадь поперечного сечения элементов конструкции. И из условия Тд  Тф, где Тд, Tф – работа действительных и фиктивных сил на перемещениях при потере устойчивости, вычисляют критическую нагрузку Pкрд и сравнивают ее с предельно возможной нагрузкой Pпред, действующей на конструкцию, и при Pкрд Тф, где Тд, Tф – работа действительных и фиктивных сил на перемещениях при потере устойчивости, вычисляют критическую нагрузку Pкрд и сравнивают ее с предельно возможной нагрузкой Pпред, действующей на конструкцию, и при Pкрд 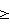 Pпред делают вывод о потере устойчивости конструкции.
Способ может характеризоваться тем, что критическую нагрузку определяют из условия Pпред делают вывод о потере устойчивости конструкции.
Способ может характеризоваться тем, что критическую нагрузку определяют из условия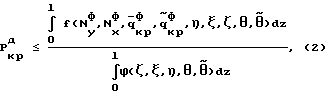 где l – длина элемента конструкции, z – продольная координата. Входящие в систему уравнений (1) критические нагрузки и изгибно-крутильные деформации представляют собой Nyф, Nxф – критические осевые фиктивные нагрузки, действующие в плоскостях ZOX и ZOY соответственно, определяемые из граничных условий. 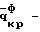 критическая фиктивная нагрузка поперечного обжатия, при чисто крутильной форме потери устойчивости, определяемая из граничных условий. критическая фиктивная нагрузка поперечного обжатия, при чисто крутильной форме потери устойчивости, определяемая из граничных условий. 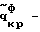 то же, что и то же, что и 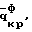 но при свободном кручении. E, G – модуль Юнга при сжатии и кручении соответственно. но при свободном кручении. E, G – модуль Юнга при сжатии и кручении соответственно.  – продольные перемещения элемента конструкции вдоль оси Z. – продольные перемещения элемента конструкции вдоль оси Z.  – прогиб элемента конструкции в плоскости ZOX. – прогиб элемента конструкции в плоскости ZOX.  – прогиб элемента конструкции в плоскости ZOY. – прогиб элемента конструкции в плоскости ZOY. 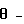 угол закручивания элемента конструкции при чисто крутильной форме потери устойчивости элементов конструкции. угол закручивания элемента конструкции при чисто крутильной форме потери устойчивости элементов конструкции. 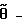 угол закручивания элемента конструкции при депланирующей форме потери устойчивости элементов конструкции. h – высота поперечного сечения элемента конструкции.
В основе изобретения лежат следующие предпосылки и теоретические обоснования. При исследовании проблемы устойчивости большое внимание уделяется постановке задачи о центрально сжатом стержне. В дополнении к Эйлеровской концепции устойчивости (потеря устойчивости “в малом”) в патентуемом изобретении предлагается новая концепция закритических состояний элементов конструкции – потеря устойчивости “в большом”, предполагающая возможность варьирования классами нагрузок.
Эта концепция, понятие “аналогия” в форме потери устойчивости и теорема об аналогии позволили обосновать метод аналогии в устойчивости (см. А.П. Лещенко. “Строительная механика тонкостенных конструкций”. М.: Стройиздат. 1989, с. 95 и далее) [4], которые лежат в основе патентуемого способа контроля потери устойчивости металлических строительных конструкций. Вариационный метод и новые подходы позволили значительно уточнить физику явления и получить результаты, хорошо согласующиеся с научным экспериментом и основными законами механики.
Сущность изобретения поясняется на примерах расчета критических нагрузок тонкостенных стержневых конструкций, примеры которых представлены на чертежах: угол закручивания элемента конструкции при депланирующей форме потери устойчивости элементов конструкции. h – высота поперечного сечения элемента конструкции.
В основе изобретения лежат следующие предпосылки и теоретические обоснования. При исследовании проблемы устойчивости большое внимание уделяется постановке задачи о центрально сжатом стержне. В дополнении к Эйлеровской концепции устойчивости (потеря устойчивости “в малом”) в патентуемом изобретении предлагается новая концепция закритических состояний элементов конструкции – потеря устойчивости “в большом”, предполагающая возможность варьирования классами нагрузок.
Эта концепция, понятие “аналогия” в форме потери устойчивости и теорема об аналогии позволили обосновать метод аналогии в устойчивости (см. А.П. Лещенко. “Строительная механика тонкостенных конструкций”. М.: Стройиздат. 1989, с. 95 и далее) [4], которые лежат в основе патентуемого способа контроля потери устойчивости металлических строительных конструкций. Вариационный метод и новые подходы позволили значительно уточнить физику явления и получить результаты, хорошо согласующиеся с научным экспериментом и основными законами механики.
Сущность изобретения поясняется на примерах расчета критических нагрузок тонкостенных стержневых конструкций, примеры которых представлены на чертежах:на фиг. 1 показана схема нагружения упругого элемента действительными нагрузками I класса; на фиг. 2 – схема нагружения упругого элемента фиктивными нагрузками II класса; на фиг. 3 – поперечное сечение опытного образца (опыт 1); на фиг. 4 – поперечное сечение опытного образца (опыт 2). Контроль потери устойчивости металлических строительных конструкций по заявляемому способу осуществляют следующим образом. Для стержня (на фиг. 1 и 2) с нагрузкой внецентренного сжатия Nд выделяют наиболее опасную изгибную форму потери устойчивости в плоскости ZOX и вычисляют критическую нагрузку по условию (2), которая в данном случае имеет вид ([4], стр. 131): 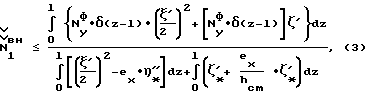 где  * – деформации изгиба в плоскости ZOY, определяемые деформационным расчетом * – деформации изгиба в плоскости ZOY, определяемые деформационным расчетом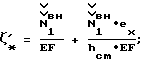  * – суммарная продольная деформация внецентренно сжатого стержня; * – суммарная продольная деформация внецентренно сжатого стержня; (z-l) – дельта-функция Дирака.
Расчет внецентренно сжатого стержня (см. фиг. 3) по формуле (3) дает следующий результат: (z-l) – дельта-функция Дирака.
Расчет внецентренно сжатого стержня (см. фиг. 3) по формуле (3) дает следующий результат: 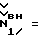 2430 дан.
Соответственно, для стержня с другими размерами поперечного сечения (см. фиг. 4) имеем 2430 дан.
Соответственно, для стержня с другими размерами поперечного сечения (см. фиг. 4) имеем 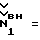 1147 дан.
Отметим, что проведенный расчет хорошо согласуется с экспериментом, уточняет физику явления, а при сопоставлении результата с данными, полученными для аналогичной расчетной схемы по ближайшему аналогу [1], выявлена погрешность 42% и 58,7%, идущая не в запас прочности на устойчивость (см. табл. 1). Далее рассмотрим случай определения потери устойчивости для другого вида нагрузок – поперечной нагрузки, воздействующей на стержень (фиг. 1, 2). Критические нагрузки для Pд, qд и Мд вычисляют по формулам 1147 дан.
Отметим, что проведенный расчет хорошо согласуется с экспериментом, уточняет физику явления, а при сопоставлении результата с данными, полученными для аналогичной расчетной схемы по ближайшему аналогу [1], выявлена погрешность 42% и 58,7%, идущая не в запас прочности на устойчивость (см. табл. 1). Далее рассмотрим случай определения потери устойчивости для другого вида нагрузок – поперечной нагрузки, воздействующей на стержень (фиг. 1, 2). Критические нагрузки для Pд, qд и Мд вычисляют по формулам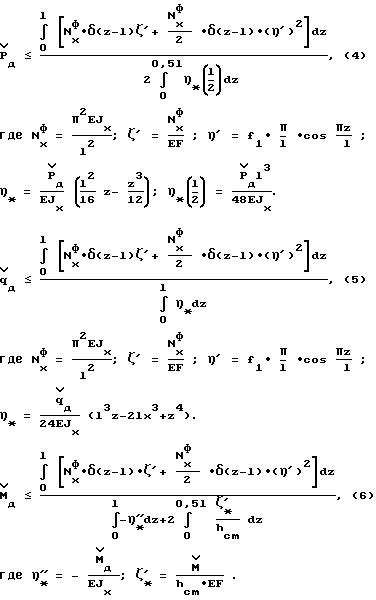 Полученные результаты по определению критических нагрузок сведены в таблицу 2. В этой же таблице для сравнения приведены данные, рассчитанные по известным формулам (1) с привлечением конкретных формул из книги: “Прочность, устойчивость и колебания”, Справочник в 3-х томах под редакцией И.А. Биргера, 1968 г. [5]. Приведенные в табл. 2 расчеты показывают, что патентуемый способ контроля потери устойчивости металлических строительных конструкций значительно уточняет физическую модель потери устойчивости строительной конструкции и позволяет тем самым повысить надежность конструкции в эксплуатации. Формула изобретения
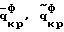 , вызывающие изгибно-крутильную форму потери устойчивости и изгибно-крутильные деформации , вызывающие изгибно-крутильную форму потери устойчивости и изгибно-крутильные деформации 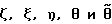 из системы дифференциальных уравнений устойчивости из системы дифференциальных уравнений устойчивости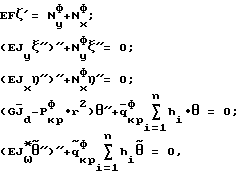 где Jx – момент инерции поперечного сечения элементов конструкции относительно оси OX; Jy – момент инерции площади поперечного сечения элементов конструкции при раздельном кручении относительно оси OY; 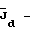 крутильный момент инерции поперечного сечения элементов конструкции при раздельном кручении; крутильный момент инерции поперечного сечения элементов конструкции при раздельном кручении;J*  – раздельный секторальный момент инерции поперечного сечения элементов конструкции; – раздельный секторальный момент инерции поперечного сечения элементов конструкции;F – площадь поперечного сечения элементов конструкции;  – продольные перемещения элемента конструкции вдоль оси OZ; – продольные перемещения элемента конструкции вдоль оси OZ; – прогиб элемента конструкции в плоскости ZOX; – прогиб элемента конструкции в плоскости ZOX; – прогиб элемента конструкции в плоскости ZOY; – прогиб элемента конструкции в плоскости ZOY;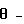 угол закручивания элемента конструкции при чисто крутильной форме потери устойчивости элементов конструкции; угол закручивания элемента конструкции при чисто крутильной форме потери устойчивости элементов конструкции;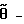 угол закручивания элемента конструкции при депланирующей форме потери устойчивости элементов конструкции; угол закручивания элемента конструкции при депланирующей форме потери устойчивости элементов конструкции;h – высота поперечного сечения элемента конструкции; из условия Tд  Tф, где Tд, Tф – работа действительных и фиктивных сил на перемещениях при потере устойчивости, вычисляют критическую нагрузку Tф, где Tд, Tф – работа действительных и фиктивных сил на перемещениях при потере устойчивости, вычисляют критическую нагрузку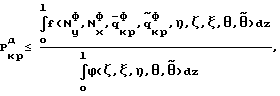 где l – длина стержня; z – продольная координата, сравнивают ее с предельно возможной нагрузкой Pпред, действующей на конструкцию, и при Pкрд 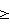 Pпред делают вывод о потере устойчивости конструкции. Pпред делают вывод о потере устойчивости конструкции.
РИСУНКИ
MM4A – Досрочное прекращение действия патента СССР или патента Российской Федерации на изобретение из-за неуплаты в установленный срок пошлины за поддержание патента в силе
Дата прекращения действия патента: 05.02.2007
Извещение опубликовано: 20.01.2008 БИ: 02/2008
|
||||||||||||||||||||||||||
