Патент на изобретение №2208809

(54) СПОСОБ ОДНОЧАСТОТНОГО ОПРЕДЕЛЕНИЯ ЗАДЕРЖКИ СИГНАЛОВ НАВИГАЦИОННОЙ СПУТНИКОВОЙ СИСТЕМЫ В ИОНОСФЕРЕ

(57) Реферат:

Изобретение относится к области спутниковой навигации и может быть использовано для определения ионосферной задержки распространения сигналов глобальных навигационных спутниковых систем с помощью навигационной аппаратуры потребителей глобальной навигационной спутниковой системы, работающей на одной частоте. В предлагаемом способе определение задержки сигналов в ионосфере производится путем решения системы уравнений, составленной по разностям приращений псевдодальностей, измеренных по дальномерному коду и по фазе несущей частоты для каждого навигационного космического аппарата. Достигаемым техническим результатом изобретения является упрощение способа оценки задержки сигналов в ионосфере, а также повышение его быстродействия. 1 ил.

Изобретение относится к области спутниковой навигации и может быть использовано для определения ионосферной задержки распространения сигналов глобальных навигационных спутниковых систем (ГНСС) с помощью навигационной аппаратуры потребителей (НАП) ГНСС, работающей на одной частоте.

Известен способ определения задержки сигналов ГНСС в ионосфере на одной частоте [1, С. 125-128], основанный на применении упрощенной модели ионосферы. Исходными данными для расчета ионосферных поправок являются приближенные значения координат НАП ГНСС, угол места, азимут навигационных космических аппаратов (НКА), время и коэффициенты модели. Коэффициенты модели передаются в навигационном сообщении системы GPS и обновляются каждые 6 дней [1, С.114].

Недостатком данного способа является, низкая точность определения задержки сигналов в ионосфере. Применение упрощенной модели ионосферы позволяет уменьшить, как минимум, в два раза влияние ионосферы на среднеквадратическую погрешность определения положения НАП ГНСС [1, С.125]. С большей погрешностью эта модель предсказывает поведение ионосферы в экваториальных и высоких широтах [2, С.85].

Величина задержки сигналов в ионосфере на практике зависит от солнечной активности (11-летний цикл), сезонных и ежедневных вариаций, угла места и азимута НКА, а также от широты и долготы расположения НАП ГНСС. Величина погрешности измерения псевдодальности за счет задержки сигнала в ионосфере может лежать в пределах от 0.15 до 50 метров [3, С.104].

Ионосфера, главным образом, влияет на величину погрешностей измерения псевдодальностей, измеренных по дальномерному коду и по фазе несущей частоты.

Известен способ определения задержки сигналов в ионосфере на одной частоте [4], заключающийся в определении разности между псевдодальностями, измеренными по дальномерному коду и по фазе несущей частоты, основанный на том, что в ионосфере скорость распространения фазы сигнала несущей частоты больше скорости света в свободном пространстве настолько, насколько скорость распространения модулирующего сигнала меньше скорости света. Разность измерений псевдодальности по дальномерному коду и по фазе несущей частоты равна удвоенной ионосферной задержке сигнала и может быть использована для ее определения, путем решения следующей системы уравнений [4]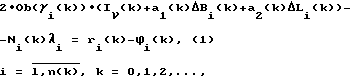

где Ob(_i(k)) – функция для пересчета вертикальной задержки в наклонную; _i(k) – угол места i-го НКА в k-й момент времени; I(k) – вертикальная задержка сигнала в ионосфере; a₁(k), a₂(k) коэффициенты полинома, аппроксимирующего горизонтальную вариацию вертикальной задержки сигнала в ионосфере; B_i(k),L_i(k) – расстояния, соответственно, по широте и долготе от подионосферной точки до точки размещения НАП ГНСС; r_i(k) – псевдодальность, измеренная по дальномерному коду; _i(k) – псевдодальность, измеренная по фазе несущей частоты; N_i(k) – начальная неоднозначность измерений фазы несущей частоты; _i – длина волны сигнала; n(k) – число радиовидимых НКА.

Полученная, путем решения системы уравнений (1) вертикальная задержка сигнала в ионосфере (для НКА с углом места _i(k) = 90<sup>), с учетом горизонтальной вариации пересчитывается в значение задержки сигнала i-го НКА с углом места _i(k)<90

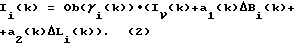Оценка величины вертикальной задержки сигналов и начальной неоднозначности фазовых измерений в данном способе производится при помощи фильтра Калмана. Вектор состояния фильтра Калмана включает вертикальную задержку, начальные фазовые неоднозначности, а также коэффициенты полинома, аппроксимирующего горизонтальную вариацию вертикальной задержки сигнала в ионосфере. Размерность вектора состояния, используемого в фильтре, зависит от числа НКА и аппроксимирующего полинома. В данном способе размерность вектора состояния равна m=n(k)+3 [4].</sup>

Недостатком прототипа является большая размерность вектора состояния, что влечет за собой большой объем вычислений при его реализации, а также увеличивает время сходимости. Начальные фазовые неоднозначности, которые входят в состав вектора состояния, приходится заново оценивать при кратковременной потере сигнала НКА и срыве процесса слежения за несущей НКА, а также при появлении нового НКА [4]. При оценке начальных фазовых неоднозначностей не учитывается их целочисленность. Все это снижает быстродействие и устойчивость работы, уменьшает скорость сходимости алгоритма, реализующего известный способ.

В основу изобретения положена задача упрощения способа оценки задержки сигналов в ионосфере, а также повышение его быстродействия.

Поставленная задача решается тем, что в способе одночастотного определения задержки сигналов навигационной спутниковой системы в ионосфере, по которому измеряют псевдодальности по дальномерному коду и по фазе несущей частоты, согласно изобретению дополнительно определяют приращения псевдодальностей за время между текущим и предыдущим измерениями, затем определяют разности приращений псевдодальностей, а задержку сигнала в ионосфере определяют из системы уравнений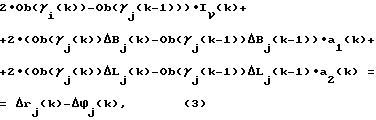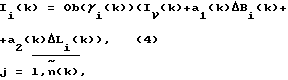


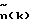где r_j(k) = r_j(k)-r_j(k-1) – приращение псевдодальности, измеренной по дальномерному коду; _j(k) = _j(k)-_j(k-1) – приращение псевдодальности, измеренной по фазе несущей частоты; – число НКА, которые были радиовидимы одновременно в моменты времени k и k -1.

Уравнения (3) получены следующим образом. Из каждого уравнения (1) в момент времени k для i-го НКА вычитается соответствующее уравнение для момента времени k-1, номера НКА должны совпадать. В итоге получается система уравнений, где число неизвестных равно числу уравнений. Особенностью уравнений (3) является отсутствие фазовых неоднозначностей _i(k).

При практической реализации данного способа, на основе фильтра Калмана, размерность вектора состояния постоянна и равна m=3, что на несколько порядков уменьшает объем вычислений по сравнению со способом [4], т.к. объем вычислений на один шаг фильтрации пропорционален кубу размерности вектора состояния [5, С.22]. Предлагаемый способ не требует оценки или раскрытия начальных фазовых неоднозначностей.

Представленный способ может быть реализован в НАП, структурная схема которой приведена, например, в [2, С.157].

На фиг. 1 приведена блок-схема алгоритма, реализующего предлагаемый способ. В соответствии с блок-схемой, сначала инициализируют переменную j (оператор 1). Затем проверяют условие окончания цикла (оператор 2). Далее вычисляют приращение псевдодальности j-го НКА, измеренной по дальномерному коду (оператор 3). Затем вычисляют приращение псевдодальности j-го НКА, измеренной по фазе несущей частоты (оператор 4). Вычисляют разность приращений псевдодальностей j-го НКА (оператор 5) и записывают в вектор измерений фильтра Калмана. После чего увеличивают на единицу переменную j (оператор 6). После выполнения условия окончания цикла сформированный вектор измерений поступает в блок, где реализуется фильтр Калмана (оператор 7), описанный, например в [5, С.26-29]. С помощью фильтра Калмана оценивают вертикальную задержку сигнала в ионосфере и коэффициенты полинома, аппроксимирующего горизонтальную вариацию вертикальной задержки сигнала. Затем инициализируют переменную i (оператор 8) и проверяют условие продолжения цикла (оператор 9). Далее вычисляют задержку сигнала в ионосфере для i-го НКА (операторы 10) и увеличивают на единицу переменную i (оператор 11). После выполнения условия окончания цикла (оператор 9) вычисления заканчиваются.

Результатом вычислений являются задержки сигналов в ионосфере всех радиовидимых НКА на k-й момент времени. Полученные задержки сигналов НКА в ионосфере применяются для коррекции измеренных псевдодальностей.

Литература
1. ICD-GPS-200, Revision C, U.S. Government, October 10, 1993.

Сетевые спутниковые радионавигационные системы. /В.С. Шебшаевич, П.П. Дмитриев, Н. В. Иванцевич и др.; Под ред. В.С. Шебшаевича. – 2-е изд., перераб. И доп. – М.: Радио и связь, 1993. – 408 с.

3. Hofmann-Wellenhof B., Lichtenegger H., Collins J. Global Positioning System. Theory and Practice. Springer-Verlag Wien New York, 1994. – 356 p.

^th International conference on “Differential Satellite Navigation Systems”, Additional Volume, St. Petersburg, Russia, May, 1996.

5. Гришин Ю.П., Казаринов Ю.М. Динамические системы, устойчивые к отказам. – М.: Радио и связь, 1985. – 176 с.

Формула изобретения

Способ одночастотного определения задержки сигналов навигационной спутниковой системы в ионосфере, по которому измеряют псевдодальности по дальномерному коду и по фазе несущей частоты, отличающийся тем, что дополнительно определяют приращения псевдодальностей за время между текущим и предыдущим измерениями, затем определяют разности приращений псевдодальностей, а задержку сигнала в ионосфере определяют из системы уравнений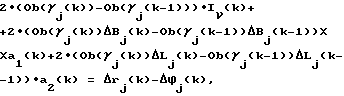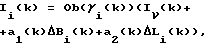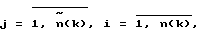



где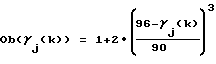

– функция для пересчета вертикальной задержки в наклонную;
_j(k) – угол места j-го навигационного космического аппарата (НКА);
I(k) – вертикальная задержка сигнала в ионосфере;
a₁(k), a₂(k) – коэффициенты полинома, аппроксимирующего горизонтальную вариацию вертикальной задержки сигнала в ионосфере;
B_j(k), L_j(k) – расстояния, соответственно, по широте и долготе от подионосферной точки до точки размещения навигационной аппаратуры потребителей глобальной навигационной спутниковой системы (НАП ГНСС);
r_j(k) = r_j(k)-r_j(k-1) – приращение псевдодальности, измеренной по дальномерному коду;
_j(k) = _j(k)-_j(k-1) – приращение псевдодальности, измеренной по фазе несущей частоты;
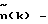число НКА, которые были радиовидимы одновременно в моменты времени k и k-1;
n(k) – число радиовидимых НКА в k-й момент времени.

РИСУНКИ