Патент на изобретение №2189069
|
||||||||||||||||||||||||||
(54) СПОСОБ АДАПТИВНОЙ АВТОМАТИЧЕСКОЙ САМОНАСТРОЙКИ МНОГОПАРАМЕТРИЧЕСКИХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ НА ОПТИМАЛЬНЫЕ УСЛОВИЯ
(57) Реферат: Изобретение относится к автоматической оптимизации многопараметрических объектов управления, обладающих одноэкстремальной функцией качества, основанной на каком-либо критерии оптимальности. Технический результат заключается в повышении быстродействия самонастройки. Способ заключается в следующем. В пространстве оптимизируемых параметров из исходного состояния делается шаг в случайном направлении в соответствии с равномерным законом распределения. Если значение функции качества в новом состоянии больше или равно значению функции качества в исходной точке, то система возвращается в первоначальное состояние; после чего снова формируется случайный шаг, отсчитанный из старого состояния. Адаптация распределения направления случайных шагов заключается в изменении их математического ожидания на основе знака приращения функции качества, а адаптация интенсивности самообучения – в зависимости от абсолютного значения разности производной функции качества оптимизируемого объекта при удачных пробах. 1 табл., 1 ил. Изобретение относится к автоматической оптимизации многопараметрических объектов управления, обладающих одноэкстремальной функцией качества, основанной на каком-либо критерии оптимальности. Известны способы случайного поиска экстремума функции качества одноэкстремальных многопараметрических объектов, заключающиеся в формировании случайных входных шаговых воздействий на объект управления [1]. Недостатком таких способов является отсутствие адаптации интенсивности самообучения, что приводит к значительному снижению их эффективности и быстродействия. Наиболее близким к изобретению по технической сущности является способ, основанный на формировании случайных равномерно распределенных входных шаговых воздействий на объект управления и адаптации их распределения и интенсивности самообучения [2]. Недостатком этого способа является невысокое быстродействие поиска на объектах управления, обладающих овражной функцией качества, так как алгоритм адаптации интенсивности самообучения не учитывает особенностей рельефа функции качества оптимизируемого объекта. Предлагаемый способ заключается в том, что создается режим адаптивного случайного поиска в пространстве оптимизируемых параметров, основанный на формировании случайных входных шаговых воздействий на объект управления, распределенных по равномерному закону, математическое ожидание которых автоматически адаптируется в зависимости от сигнала, поступающего с выхода объекта по каналу обратной связи, а адаптация интенсивности самообучения в процессе поиска осуществляется при удачном случайном шаге в зависимости от абсолютного значения разности производной функции качества оптимизируемого объекта, получаемого на основе сигнала, поступающего с выхода объекта по каналу обратной связи. На чертеже представлена блок-схема алгоритма, реализующего предлагаемый способ автоматической настройки многопараметрических систем автоматического управления на оптимальные условия (вариант алгоритма с пересчетом, для определенности представлен случай минимизации функции качества). Способ реализуется с помощью алгоритма, блок-схема которого включает в себя: 1 – блок формирования шага в случайном направлении в пространстве оптимизируемых параметров в соответствии с равномерным законом распределения, 2 – блок запоминания сформированного шага, 3 – блок определения значения функции качества в новой точке пространства оптимизируемых параметров, 4 – блок определения знака приращения функции качества, 7 – блок запоминания значения функции качества при удачном шаге, 5 и 8 – блоки адаптации распределения направления поисковых шагов и интенсивности самообучения в процессе настройки, 6 – блок формирования шага в обратном направлении при неудачном шаге. Предлагаемый способ реализуется следующим образом. В пространстве оптимизируемых параметров из исходного состояния Xi делается шаг в случайном направлении в соответствии с равномерным законом распределения. Если значение функции качества в новом состоянии Q(Xi+1) больше или равно значению функции качества в исходной точке Q(Xi), то есть случайная проба оказалась неудачной (задача минимизации), то система возвращается в первоначальное состояние Xi, после чего снова формируется случайный шаг, отсчитанный из старого состояния. Рекуррентная формула для смещения в пространстве оптимизируемых параметров по этому алгоритму имеет следующий вид: 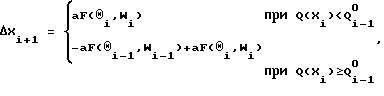 где Q0 i = minQ(Xj), j = 1,…, i – наименьшее значение функции качества за i предыдущих шагов поиска, F(  ,W) – единичный вектор, определяющий направление случайного шага ,W) – единичный вектор, определяющий направление случайного шага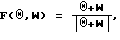 где  – единичный случайный вектор, равномерно распределенный по всем направлениям пространства оптимизируемых параметров с нулевым математическим ожиданием, – единичный случайный вектор, равномерно распределенный по всем направлениям пространства оптимизируемых параметров с нулевым математическим ожиданием,W – вектор памяти (математическое ожидание направления случайных шагов), реализующий адаптацию распределения направления шагов, а – величина рабочего шага. Адаптация распределения направления случайных шагов заключается в изменении их математического ожидания на основе знака приращения функции качества (блоки 5 и 8 на чертеже). Алгоритм непрерывной адаптации математического ожидания случайных шагов можно представить в виде следующего векторного рекуррентного соотношения Wi+1 = kWi–   Qi Qi Xi, Xi,где W – математическое ожидание равномерно распределенных случайных шагов, k – коэффициент запоминания (0  k k  1), 1), – параметр скорости обучения (0 – параметр скорости обучения (0    1).
Коэффициенты k и 1).
Коэффициенты k и  определяют интенсивность самообучения в процессе поиска.
При работе по этому алгоритму адаптации вектор W стремится перестроиться в направлении, обратном градиенту функции качества оптимизируемого объекта, то есть шаги поиска будут в среднем направлены в сторону быстрейшего уменьшения функции качества.
Адаптация интенсивности самообучения в процессе оптимизации (блок 8 на чертеже) осуществляется с помощью следующих выражений для коэффициентов k и определяют интенсивность самообучения в процессе поиска.
При работе по этому алгоритму адаптации вектор W стремится перестроиться в направлении, обратном градиенту функции качества оптимизируемого объекта, то есть шаги поиска будут в среднем направлены в сторону быстрейшего уменьшения функции качества.
Адаптация интенсивности самообучения в процессе оптимизации (блок 8 на чертеже) осуществляется с помощью следующих выражений для коэффициентов k и  : :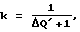 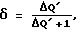 где  Q Q – оценка разности производной функции качества в i-й и i-1-й точках траектории движения системы к экстремуму функции качества объекта оптимизации, получаемая при удачных шагах поиска – оценка разности производной функции качества в i-й и i-1-й точках траектории движения системы к экстремуму функции качества объекта оптимизации, получаемая при удачных шагах поиска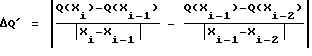 Смысл этого алгоритма адаптации интенсивности самообучения заключается в следующем. Если в двух точках траектории движения системы к экстремуму разность значений производной функции качества мала по модулю, то нет необходимости интенсивно обучаться, то есть принимать весь опыт последнего шага оптимизации, и параметр скорости обучения  мал, в то время как коэффициент запоминания приобретенного опыта k велик. Если при очередном шаге разность значений производной функции качества оказалась велика, то есть ситуация достаточно резко изменилась, то нет надобности запоминать весь предыдущий накопленный опыт оптимизации, и коэффициент запоминания k принимает малое значение, в то время как мал, в то время как коэффициент запоминания приобретенного опыта k велик. Если при очередном шаге разность значений производной функции качества оказалась велика, то есть ситуация достаточно резко изменилась, то нет надобности запоминать весь предыдущий накопленный опыт оптимизации, и коэффициент запоминания k принимает малое значение, в то время как  велико, то есть при изменении ситуации поиска, связанном с особенностями рельефа функции качества, происходит интенсивное обучение на основе нового опыта.
Достигаемый технический эффект от применения предлагаемого способа позволяет уменьшить потери на поиск и значительно повысить быстродействие отыскания экстремума овражных функций качества объектов оптимизации: экспериментальные исследования, проведенные на модельных функциях, показали, что выигрыш в быстродействии предлагаемого способа по сравнению с прототипом составил от 2 до почти 15 процентов в зависимости от вида модельной функции (см. таблицу), и, как ожидалось, максимальный выигрыш в производительности имел место при оптимизации модельного объекта, обладающего функцией качества с ярко выраженной овражностью. Поскольку реальные объекты автоматического управления очень часто имеют овражные функции качества, то применение предлагаемого способа оказывается целесообразным для их эффективной оптимизации.
Центральная модель: велико, то есть при изменении ситуации поиска, связанном с особенностями рельефа функции качества, происходит интенсивное обучение на основе нового опыта.
Достигаемый технический эффект от применения предлагаемого способа позволяет уменьшить потери на поиск и значительно повысить быстродействие отыскания экстремума овражных функций качества объектов оптимизации: экспериментальные исследования, проведенные на модельных функциях, показали, что выигрыш в быстродействии предлагаемого способа по сравнению с прототипом составил от 2 до почти 15 процентов в зависимости от вида модельной функции (см. таблицу), и, как ожидалось, максимальный выигрыш в производительности имел место при оптимизации модельного объекта, обладающего функцией качества с ярко выраженной овражностью. Поскольку реальные объекты автоматического управления очень часто имеют овражные функции качества, то применение предлагаемого способа оказывается целесообразным для их эффективной оптимизации.
Центральная модель: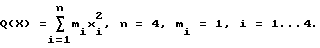 Центральная модель является моделью сепарабельного объекта управления, у которого отсутствует перекрестное влияние входных параметров. Квадратичная модель: 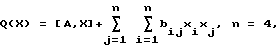 где [A,X] – скалярное произведение вектора параметрических коэффициентов А = (а1,а2,а3,а4)T и вектора входных координат Х = (х1,х2,х3,х4)T, аi = 1, i = 1…4, bij – элементы матрицы 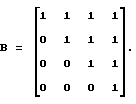 Квадратичная модель имеет более сложную структуру по сравнению с центральной и моделирует несепарабельный объект с перекрестным влиянием параметров. Функция Пауэла: Q(X) = (х1 + 10х2)2 + 5(х3 – х4)4 + (х2 – 2х3)4 + 10(х1 – x4)4. Функция Пауэла моделирует объект оптимизации с ярко выраженной овражностью функции качества. Все модельные функции имеют один минимум при хi = 0, i = 1…4. При проведении сравнительного тестирования использовался одинаковый для всех моделей набор из ста начальных точек поиска, координаты которых представляли собой случайные равномерно распределенные числа в пределах от минус 10 до плюс 10. Цикл поиска экстремума для каждой начальной точки повторялся 1000 раз. Для всех трех моделей параметры поиска были одинаковыми: коэффициент запоминания k = 0,7; параметр скорости обучения  = 0,1, шаг а = 0,15. Поиск экстремума производился с точностью до 0,01.
СПИСОК ЛИТЕРАТУРЫ = 0,1, шаг а = 0,15. Поиск экстремума производился с точностью до 0,01.
СПИСОК ЛИТЕРАТУРЫ1. Растригин Л.А. Системы экстремального управления. – М.: Наука, 1974, с. 422-446. 2. Растригин Л.А., Рипа К.К., Тарасенко Г.С. Адаптация случайного поиска. – Рига: Зинатие, 1978, с. 148-150 (прототип). Формула изобретения
Wi+1 = kWi–   Qi Qi Xi, Xi,где W – математическое ожидание равномерно распределенных случайных шагов; k – коэффициент запоминания;  – параметр скорости самообучения; – параметр скорости самообучения;Q – функция качества; X – состояние объекта в пространстве оптимизируемых параметров, отличающийся тем, что коэффициент запоминания и параметр скорости самообучения при адаптации распределения направления случайных входных шаговых воздействий автоматически адаптируют при удачных пробных шагах в зависимости от абсолютного значения разности производной функции качества оптимизируемого объекта, получаемого на основе сигнала, поступающего с выхода объекта по каналу обратной связи, в соответствии с выражениями 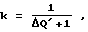 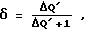 где 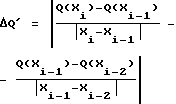 – абсолютное значение разности производной функции качества оптимизируемого объекта. РИСУНКИ
MM4A Досрочное прекращение действия патента Российской Федерации на изобретение из-за неуплаты в установленный срок пошлины за поддержание патента в силе
Дата прекращения действия патента: 08.08.2002
Номер и год публикации бюллетеня: 16-2004
Извещение опубликовано: 10.06.2004
|
||||||||||||||||||||||||||
