Патент на изобретение №2189014
|
||||||||||||||||||||||||||
(54) ИЗМЕРИТЕЛЬНЫЙ МОДУЛЬ
(57) Реферат: Изобретение может быть использовано в устройствах для измерения расхода газов или жидкостей времяпролетным ультразвуковым методом. Измерительный модуль в виде цилиндра встроен в трубопровод круглого сечения. В стенки модуля вмонтированы пары двунаправленных приемно-излучательных элементов, формирующих n0 основных, параллельных оси модуля и n0-1 дополнительных скошенных измерительных плоскостей. Каждая скошенная измерительная плоскость образована или приемно-излучательными элементами предыдущей и последующей основной измерительной плоскости или приемно-излучательными элементами предыдущей и отражательной площадкой последующей основной измерительной плоскости. Изобретение обеспечивает повышение точности определения расхода. 4 з. п.ф-лы, 6 ил., 2 табл. Изобретение относится к области высокоточных методов измерения расхода (объема или количества жидкости или газа, протекающего в единицу времени по каналу транспортировки) прокачиваемых через трубопроводы жидкостей или газов. Измерительный модуль встраивается в трубопровод, представляя собой после этого часть трубопровода. Измерения в измерительном модуле производятся в измерительных плоскостях, параллельных оси модуля. Регистрируя разность времен пролета ультразвуковых импульсов в измерительных плоскостях в прямом и обратном направлениях, можно вычислить расход жидкости или газа. Количество измерительных плоскостей может меняться от одной (одноплоскостные измерения) до нескольких (многоплоскостные измерения). Изобретение может найти применение как в нефтяной и газовой промышленности, так и в любых установках, содержащих каналы транспортирования жидкостей или газов. Определение объема прокачиваемых через трубы круглого сечения газов или жидкостей при использовании времяпролетных ультразвуковых измерений сводится к вычислению двумерного интеграла от аксиальной (вдоль трубы) компоненты скорости потока vz(x, y), в общем случае неоднородной по плоскости сечения трубы S[1]: 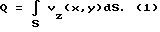 Для ультразвуковых времяпролетных измерений приближенно с точностью до малых порядка 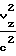 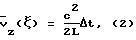 где с – скорость звука в неподвижной среде, L – расстояние между ультразвуковыми приемно-излучательными элементами (датчиками),  t – разность времен прохождения ультразвукового импульса от датчика A1 до датчика А2 в прямом и обратном направлениях и t – разность времен прохождения ультразвукового импульса от датчика A1 до датчика А2 в прямом и обратном направлениях и 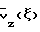 – средняя скорость потока в измерительной плоскости с расстоянием – средняя скорость потока в измерительной плоскости с расстоянием  от оси трубы с радиусом R: от оси трубы с радиусом R: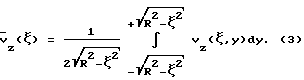 При этом возможен как отражательный режим, когда датчики находятся с одной стороны трубы, а отражательная площадка находится на другой стороне трубы, так и трансмиссионный режим, когда датчики находятся по разные стороны трубы. Известны устройства, определяющие расход с помощью цилиндрических измерительных модулей круглого сечения по результатам одного диаметрального измерения, при этом измерительная плоскость пересекает сечение трубы по диаметру [2] . При этом предполагается, что распределение аксиальной компоненты по сечению трубы является радиально симметричным vz(x,y) = vz(r), что часто выполняется с достаточно большой точностью. Однако при этом предположении 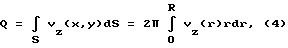 т. е. расход Q не выражается точно через 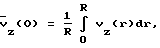 что заставляет использовать поправочные коэффициенты, зависящие от диаметра трубы и диапазона изменения vz(r).
Наиболее близким но технической сущности и достигаемому результату является устройство по патенту США 4646575 (прототип), реализующее принцип многоплоскостных измерений, т.е. определяющее расход по результатам измерений в нескольких параллельных измерительных плоскостях [3].
При этом вычисление интеграла (1) для произвольного распределения vz(x, y) сводится к численному вычислению одномерного интеграла что заставляет использовать поправочные коэффициенты, зависящие от диаметра трубы и диапазона изменения vz(r).
Наиболее близким но технической сущности и достигаемому результату является устройство по патенту США 4646575 (прототип), реализующее принцип многоплоскостных измерений, т.е. определяющее расход по результатам измерений в нескольких параллельных измерительных плоскостях [3].
При этом вычисление интеграла (1) для произвольного распределения vz(x, y) сводится к численному вычислению одномерного интеграла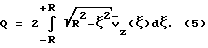 Соответствующий измерительный модуль содержит приемно-излучающие элементы, вмонтированные в стенки модуля и предназначенные для генерации и регистрации ультразвуковых импульсов, распространяющихся в основных измерительных плоскостях, параллельных оси измерительного модуля и друг другу. Так как количество измерительных плоскостей, вообще говоря, невелико, применение обычных формул численного интегрирования, таких как правила трапеций или Симпсона, дает невысокую точность. Повысить точность численного интегрирования позволяет применение квадратурных формул Ньютона, Чебышева и Гаусса [4]. Недостатком измерительного модуля по патенту США 4646575 является то, что при данном количестве n пар приемно-излучающих элементов (количестве основных измерительных плоскостей) можно использовать квадратурные формулы только до порядка n включительно. В то же время целесообразно увеличивать порядок квадратурной формулы, так как точность численного вычисления интеграла (5) возрастает с ростом n. Цель изобретения – повышение точности определения объема прокачиваемых через трубы круглого сечения газов или жидкостей при использовании многоплоскостных времяпролетных ультразвуковых измерений за счет добавления межплоскостных измерений в скошенных измерительных плоскостях, позволяющих при том же количестве n пар приемно-излучающих элементов (количестве основных измерительных плоскостей) увеличить количество измерений и, следовательно, применить квадратурные формулы численного интегрирования более высокого порядка. Цель достигается тем, что приемно-излучательные элементы выполнены двунаправленными с основным и дополнительным направлениями, задающими n0 основных измерительных плоскостей и n’=n0-1 скошенных измерительных плоскостей, причем основные измерительные плоскости параллельны друг другу, а каждая скошенная измерительная плоскость образуется либо приемно-излучательным элементами предыдущей и последующей основной измерительной плоскости, либо (при наличии отражательных площадок) приемно-излучательными элементами предыдущей и отражательной площадкой последующей основной измерительной плоскости. При этом желательно, чтобы отражательная площадка скошенной плоскости совпадала с отражательной площадкой соседней основной измерительной плоскости. Если распределение аксиальной компоненты по сечению модуля является радиально симметричным vz(x, y}=vz(r), то скошенные плоскости ничем не будут отличаться от основных измерительных плоскостей, за исключением расстояния от оси модуля  j (это расстояние необходимо отсчитывать от оси модуля по перпендикуляру к измерительной плоскости). Дополнительные (скошенные) измерительные плоскости в совокупности с основными измерительными плоскостями образуют квадратурную схему порядка n=2n0-1.
Так как квадратурные формулы зависят от расстояний измерительных плоскостей от оси модуля, в качестве частных решений задачи можно располагать основные измерительные плоскости эквидистантно, а также на расстояниях j (это расстояние необходимо отсчитывать от оси модуля по перпендикуляру к измерительной плоскости). Дополнительные (скошенные) измерительные плоскости в совокупности с основными измерительными плоскостями образуют квадратурную схему порядка n=2n0-1.
Так как квадратурные формулы зависят от расстояний измерительных плоскостей от оси модуля, в качестве частных решений задачи можно располагать основные измерительные плоскости эквидистантно, а также на расстояниях 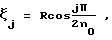 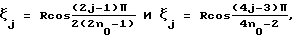 j= 1,2,3…,n0 от оси трубы с радиусом R.
При использовании квадратурных формул можно как учитывать, так и не учитывать весовой множитель j= 1,2,3…,n0 от оси трубы с радиусом R.
При использовании квадратурных формул можно как учитывать, так и не учитывать весовой множитель 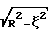 в формуле (5).
Соответственно, квадратурная формула будет выглядеть следующим образом: в формуле (5).
Соответственно, квадратурная формула будет выглядеть следующим образом: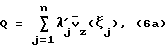 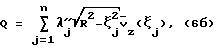 где n – количество измерительных плоскостей,  j – расстояние j-й измерительной плоскости от оси трубы (узлы квадратурной формулы), j – расстояние j-й измерительной плоскости от оси трубы (узлы квадратурной формулы),  j – коэффициенты квадратурной формулы. При этом даже небольшое увеличение количества измерительных плоскостей приводит к резкому повышению точности результата.
Квадратурные формулы различаются постановкой задачи оптимизации вычисления суммы (6): j – коэффициенты квадратурной формулы. При этом даже небольшое увеличение количества измерительных плоскостей приводит к резкому повышению точности результата.
Квадратурные формулы различаются постановкой задачи оптимизации вычисления суммы (6):Задача 1. Для заданного расположения узлов  j найти наилучшие значения коэффициентов j найти наилучшие значения коэффициентов  j; наиболее известна задача для равноотстоящих узлов j; наиболее известна задача для равноотстоящих узлов  j – формулы Ньютона-Котеса.
Задача 2. Для заданных значений коэффициентов j – формулы Ньютона-Котеса.
Задача 2. Для заданных значений коэффициентов  j найти наилучшее расположение узлов j найти наилучшее расположение узлов  j; наиболее известна задача для равных коэффициентов j; наиболее известна задача для равных коэффициентов  j – формулы Чебышева.
Задача 3. Найти наилучшее расположение узлов j – формулы Чебышева.
Задача 3. Найти наилучшее расположение узлов  j и соответствующие значения коэффициентов j и соответствующие значения коэффициентов  j/ – формулы Гаусса.
Коэффициенты квадратурной формулы как с учетом ( j/ – формулы Гаусса.
Коэффициенты квадратурной формулы как с учетом (  ) так и без учета ( ) так и без учета (  ) весового множителя ) весового множителя 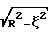 при эквидистантном расположении узлов (измерительных плоскостей) при эквидистантном расположении узлов (измерительных плоскостей)  j могут быть найдены численно [4]. Задача 3 имеет аналитическое решение [5] . С учетом весового множителя j могут быть найдены численно [4]. Задача 3 имеет аналитическое решение [5] . С учетом весового множителя 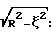 узлы узлы 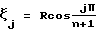 (n – количество измерительных плоскостей), а коэффициенты (n – количество измерительных плоскостей), а коэффициенты 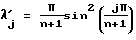 . Без учета весового множителя . Без учета весового множителя 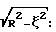 узлы узлы  j являются нулями многочленов Лежандра Pn( j являются нулями многочленов Лежандра Pn( j) = 0 (n – количество измерительных плоскостей), а коэффициенты j) = 0 (n – количество измерительных плоскостей), а коэффициенты 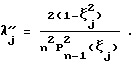 Графические изображения На фиг. 1 показана схема ультразвуковых времяпролетных измерений с отражательной площадкой (а) и без отражательной площадки (б): A1BA2 – основная измерительная плоскость, A1, А2 – датчики, В – отражательная площадка. На фиг. 2 показана схема ультразвуковых времяпролетных измерений в диаметральной основной измерительной плоскости 1ВA2 (A1, A2 – датчики, В – отражательная площадка). На фиг. 3 показана схема многоплоскостных ультразвуковых времяпролетных измерений (показаны только две основные измерительные плоскости – диаметральная и измерительная плоскость A1nBnA2n, A1n, А2n – датчики, Вn – отражательная площадка). На фиг. 4 показана схема многоплоскостных ультразвуковых времяпролетных измерений в сечении модуля (P1, Р2, Р3, Р4, Р5 – основные измерительные плоскости). На фиг. 5 показана схема многоплоскостных ультразвуковых времяпролетных измерений в сечении модуля с основными и скошенными плоскостями (P1, Р3, P5, P7, Р9 – основные измерительные плоскости, Р2, Р4, Р6, P8 – скошенные измерительные плоскости). На фиг. 6 показана схема многоплоскостных ультразвуковых времяпролетных измерений с основными и скошенными плоскостями: скощенная измерительная плоскость образуется датчиками A1n и A2n из основной n-й плоскости и отражательной площадкой Вn-1 из основной (n-1)-й плоскости. Предлагаемый встраиваемый в трубопровод измерительный модуль содержит вмонтированные в стенки измерительного модуля двунаправленные приемно-излучательные элементы с основным и дополнительным направлениями, задающими n0 основных измерительных плоскостей и n’=n0-1 скошенных измерительных плоскостей, причем основные измерительные плоскости параллельны друг другу, а каждая скошенная измерительная плоскость образуется либо приемно-излучательными элементами предыдущей и последующей основной измерительной плоскости, либо (при наличии отражательных площадок) приемно-излучательными элементами предыдущей и отражательной площадкой последующей основной измерительной плоскости. Последовательно в каждой измерительной плоскости, как основной, так и скошенной, генерируются и регистрируются ультразвуковые импульсы в прямом и обратном направлениях. По разности времен распространения вычисляются средние скорости для каждой измерительной плоскости, которые подставляются в соответствующую (зависящую от расположения измерительных плоскостей относительно оси модуля) формулу квадратурного интегрирования порядка 2n0-1 для определения расхода прокачиваемых через трубопровод жидкости или газа. Для примера в табл.1 приведены коэффициенты квадратурной формулы как с учетом (   ), так и без учета ( ), так и без учета (  ) весового множителя ) весового множителя 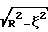 при эквидистантном расположении узлов (измерительных плоскостей) при эквидистантном расположении узлов (измерительных плоскостей)  j.
В табл. 2 приведены коэффициенты квадратурной формулы как с учетом ( j.
В табл. 2 приведены коэффициенты квадратурной формулы как с учетом (  ), так и без учета ( ), так и без учета (  ) весового множителя ) весового множителя 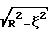 при наличии скошенных измерительных плоскостей и эквидистантном расположении основных измерительных плоскостей. Для задачи 3 справедливо вышеприведенное аналитическое решение.
Данное изобретение может найти применение в промышленных условиях, так как дает существенное увеличение точности определения расхода жидкостей или газов.
Источники информации при наличии скошенных измерительных плоскостей и эквидистантном расположении основных измерительных плоскостей. Для задачи 3 справедливо вышеприведенное аналитическое решение.
Данное изобретение может найти применение в промышленных условиях, так как дает существенное увеличение точности определения расхода жидкостей или газов.
Источники информации1. Рычагов М.Н. Ультразвуковые измерения потоков в многоплоскостных измерительных модулях. Акустический журнал, 1998, т. 44, 6, с.829-836. 2. Lynnworh L. C. Ultrasonic measurements for process control: Theory, techniques, applications. New York, Academic, 1995. 3. Патент США 4646575, МПК: G 01 F 1/66, НПК: 073.861.31 – прототип. 4. Бахвалов Н.С. Численные методы. М., Наука, 1973. – 632 с. 5. Справочник по специальным функциям. Под ред. М. Абрамовица и И. Стиган. М., Наука, 1979. – 832 с. Формула изобретения
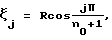 j = 1, 2, 3, . . . , n0 от оси модуля с радиусом R.
4. Измерительный модуль по п. 1, отличающийся тем, что основные измерительные плоскости расположены на расстояниях j = 1, 2, 3, . . . , n0 от оси модуля с радиусом R.
4. Измерительный модуль по п. 1, отличающийся тем, что основные измерительные плоскости расположены на расстояниях 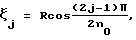 j= 1, 2, 3, . . . , n0 от оси модуля с радиусом R.
5. Измерительный модуль по п. 1, отличающийся тем, что основные измерительные плоскости расположены на расстояниях j= 1, 2, 3, . . . , n0 от оси модуля с радиусом R.
5. Измерительный модуль по п. 1, отличающийся тем, что основные измерительные плоскости расположены на расстояниях 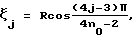 j= 1, 2, 3. . . , n0 от оси трубы с радиусом R. j= 1, 2, 3. . . , n0 от оси трубы с радиусом R.
РИСУНКИ
|
||||||||||||||||||||||||||
