Патент на изобретение №2177173

(54) УСТРОЙСТВО СКОЛЬЗЯЩЕГО ОРТОГОНАЛЬНОГО ПРЕОБРАЗОВАНИЯ СИГНАЛОВ

(57) Реферат:

Изобретение относится к вычислительной технике и может быть использовано для преобразования сигналов. Техническим результатом является повышение быстродействия. Устройство содержит входной блок памяти, выполненный в виде буфера FIFO, и основной вычислительный блок, содержащий блок памяти коэффициентов, сумматоры, арифметические блоки, каждый из которых состоит из умножителей, сумматоров и буфер FIFO. 4 з.п. ф-лы, 5 ил.

Изобретение относится к вычислительной технике, предназначено для скользящего ортогонального преобразования сигналов, которое может представлять собой прямое и обратное, комплексное и действительное спектральное преобразование (преобразование Фурье, косинусное преобразование, синусное преобразование и т.д.).

При анализе продолжительных участков сигнала, длина которых значительно превышает размер окна преобразования, используется процедура вычисления скользящего спектра, состоящая в многократном выполнении преобразования (например, быстрого преобразования Фурье БПФ) для различных положений окна преобразования относительно исходного сигнала. Как правило, эти окна перекрываются между собой, причем степень перекрытия может быть очень значительной – 75% и выше. В некоторых задачах используется шаг перемещения окна преобразования, равный 1. В этом случае достигается почти полное перекрытие. Использование алгоритмов БПФ в таких случаях является малоэффективным. Вычислительная сложность расчета всех коэффициентов преобразования для участка сигнала длины М,N-точечного БПФ и степени перекрытия составляет порядка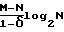

операций. При высокой степени перекрытия , близкой к 1 и больших значениях М количество необходимых операций, а следовательно, и время вычисления очень велико.

Известно много способов вычисления преобразования Фурье и его важного частного случая для приложений обработки сигналов – косинусного преобразования, синусного преобразования и многих других, использующих разложение по ортогональным базисным функциям. Один из самых распространенных способов вычислений подобного рода – быстрое преобразование Фурье БПФ (патент США N 3851162, кл. 6 G 06 F 15/34, 1974). Этот способ и устройство, его реализующее, основаны на последовательном применении БПФ для различных положений окна преобразования. Недостатками этого изобретения являются его низкое быстродействие, неэффективное использование ресурсов, ориентация на аналоговую реализацию, серьезные ограничения на размер спектрального окна анализа, низкая спектральная разрешающая способность, невозможность применения предложенного в этом изобретении способа и устройства для иных спектральных преобразований, отличных от комплексного преобразования Фурье.

Известно устройство скользящего спектрального преобразования сигналов (авторское свидетельство СССР N1363240, кл. 4 G 06 F 15/332, 1986), в состав которого входят информационный блок, два блока памяти, мультиплексор, арифметический блок, блок памяти коэффициентов, три регистра, вычитатель, сумматор и блок управления, недостатками которого являются чрезвычайно узкая направленность, невозможность осуществления обратного преобразования, ориентация исключительно на комплексный спектр, несмотря на то, что значения входного сигнала являются действительными числами, что приводит к неэффективному использованию вычислительных ресурсов, кроме того это устройство имеет всего один арифметический блок, последовательно вычисляющий значения спектральных коэффициентов, что приводит к заметному снижению быстродействия устройства.

Задачей предлагаемого изобретения является сокращение вычислительных затрат, повышение быстродействия и расширение функциональных возможностей использования преобразования для обработки различных вариантов спектров сигналов (преобразование Фурье, косинусное преобразование, синусное преобразование и т.д.).

В предлагаемом устройстве, реализующем способ скользящего ортогонального преобразования сигналов, использующий значения спектральных коэффициентов преобразования, полученные на предыдущих шагах расчета, поставленная цель достигается применением элементарных расчетных блоков, количество которых равно количеству спектральных коэффициентов преобразования, вместо одного в прототипе, для одновременного вычисления требуемого количества спектральных коэффициентов, введением нескольких разновидностей элементарных расчетных блоков, матрицы предопределенных расчетных коэффициентов, входного и результирующего сдвигового запоминающего устройства, типа FIFO и введением блока нормировочного коэффициента преобразования для осуществления как прямых, так и обратных преобразований.

Изобретение проиллюстрировано на примере наиболее часто используемого ортогонального преобразования – косинусного преобразования.

Предлагаемое устройство реализует способ вычислений, в котором использована высокая степень перекрытия окон анализа . Основная идея изобретения состоит в отказе от применения БПФ для расчета коэффициентов преобразования на каждом шаге. Вместо этого используется другой алгоритм, состоящий в том, что переход от коэффициентов одного окна преобразования к коэффициентам другого окна преобразования можно осуществить за порядка (1 – ) N операций, но при этом для косинусного преобразования нужно знать значения коэффициентов для двух последних окон преобразования. Таким образом, общая вычислительная сложность такого алгоритма со ставит всего порядка М-N операций, что при больших M (порядка сотен тысяч) и близких к 1 значениях дает значительное ускорение процесса обработки.

Введем следующие обозначения: n – шаг перемещения окна преобразования, f – исходный сигнал. f F_M, где F_M – заданное евклидово векторное пространство размерности М такое, что G^m – подпространства F_M и 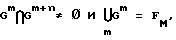где m – порядковый номер подпространства. В пространстве F_M задано скалярное произведение (f,g)_M по системе ортогональных функций g_k =(g_k0, g_k1,…, g_kM) F_M, образующих в F_M нормированный базис, где k = 0, 1,…, N-1 – порядковый номер вектора базиса, N – размер окна преобразования, f, g F_M – векторы пространства F_M. Способ, реализуемый предлагаемым устройством, позволяет вычислить коэффициенты a_k ^m = (f^m,g_k)_N, где f^m = (f_m, f_m+1, . .., f_m+N-1). Способ состоит в том, что вычисление скалярного произведения (f^m, g_k)_N можно осуществить по следующей общей формуле, справедливой для любого ортогонального преобразования с любым, даже переменным, размером окна преобразования N=N(m) и любым шагом перемещения этого окна n=n(m)
a_k ^m+n = A(a_k ^m, (f^m, g_k)_n, (f^m+N, g_k)_n),
где A – функция оконного перехода. Эта формула связывает очередные значения коэффициентов a_k ^m+n со значениями этих коэффициентов a_k ^m, полученных для предыдущих положений окна преобразования. Использование этой формулы позволяет значительно сократить вычислительные затраты. Конкретный вид функции оконного перехода A зависит от того, какое именно преобразование выполняется. Для действительного косинусного преобразования функция оконного перехода имеет вид
a_k ^m+1 = 2a_k ^mcos( k/N) – a_k ^m-1 + ((f_m+N – f_m+N-1)(-1)^k-(f_m-f_m-1))cos( k/2N),
где k= 0, 1,…, N-1 – порядковый номер вектора базиса, N- размер окна преобразования, m – порядковый номер подпространства, a_k ^m – коэффициенты преобразования, f – исходный сигнал. Для комплексного преобразования Фурье функция оконного перехода может иметь вид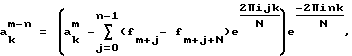

где k = 0, 1,…, N-1 – порядковый номер вектора базиса, N – размер окна преобразования, m – порядковый номер подпространства, a_k ^m – коэффициенты преобразования, f – исходный сигнал.

Предлагаемое устройство реализует описанный способ преобразования (фиг. 1 – фиг. 4) для случая косинусного преобразования.

На фиг. 1 показана общая агрегированная схема вычислителя, изображающая особенности движения потоков входных данных, управления типом осуществляемого преобразования (прямое, обратное) и структуру выходных данных. На фиг. 2 изображена структурная схема соединения арифметических блоков для случая косинусного преобразования. На фиг. 3 изображена таблица коэффициентов матрицы предопределенных расчетных коэффициентов для случая косинусного преобразования. На фиг. 4 изображена схема элементарного вычислительного блока для случая косинусного преобразования. На фиг. 5 приведена таблица результатов сравнительных испытаний различных известных способов вычисления комплексного преобразования Фурье и описанного выше способа.

Общая агрегированная схема вычислителя (фиг.1) изображает особенности движения потоков входных данных, управление типом осуществляемого преобразования (прямое, обратное) и структуру выходных данных. Схема содержит информационный вход 1, блок значений исходного сигнала 2, представляющий собой буфер FIFO, блоки 3-10, в количестве N+n+1 для косинусного преобразования, где n – шаг перемещения окна преобразования, блок нормировочных коэффициентов преобразования 11, магистрали данных 12 и 13, основной вычислительный блок 14, выходы 15, 16, и 17 (количество которых равно количеству спектральных коэффициентов, значения которых требуется получить – от 1 до N).

Схема блока 14 (фиг.2) для случая косинусного преобразования содержит матрицу предопределенных расчетных коэффициентов 18, элементарные расчетные блоки 19, 20, 21, 22, 23, количество которых равно количеству спектральных коэффициентов, выходы 24, 25, 26, 27, 28, магистраль данных 29, сумматоры 30 и 31, входы 32, 33, 34, 35.

Схема элементарного вычислительного блока 19, 20, 21, 22, 23 (фиг.4) содержит умножитель 36, сумматор 37, умножитель 38, сумматор 39, умножитель 40, буфер FIFO 41 из двух ячеек памяти 42 и 43.

Выборки f_i входного сигнала последовательно поступают на информационный вход 1, затем передаются на вход (блок 3) блока значений исходного сигнала 2, представляющего собой буфер FIFO (блоки 3 – 10), сдвигая имеющееся там значение в блок 4 и т.д. Для косинусного преобразования количество блоков 3, 4, 5, 6, 7, 8, 9, 10 равно N+n+1. По магистрали 13 данные с входных блоков 3, 4, и т.д., количество которых равно n+1 для косинусного преобразования, поступают в блок 14, где производится определение требуемых спектральных коэффициентов. Аналогичным образом по магистрали 12 данные с выходных блоков 10, 9, и т.д., количество которых равно n+1 для косинусного преобразования, поступают в блок 14. Значением на выходе блока 11, поступающим в блок 14, определяется прямое или обратное преобразование будет выполняться блоком 14. Для косинусного преобразования значение на выходе блока 11 равно 1 для прямого и 2/N для обратного преобразования. С выходов 15, 16, 17 блока 14 снимаются мгновенные значения спектральных коэффициентов, соответствующих текущему положению окна анализа. Количество выходов 15, 16, 17 блока 14 равно количеству спектральных коэффициентов, подлежащих определению – от 1 до N. Значения на этих выходах формируются в результате параллельной работы арифметических блоков 19, 20, 21, 22, 23 для косинусного преобразования, количество которых равно количеству спектральных коэффициентов, подлежащих определению. Результаты работы этих блоков по магистралям 24, 25, 26, 27, 28 поступают на выходы 15, 16, 17 блока 14.

Блок 14 в случае косинусного преобразования функционирует следующим образом (фиг. 2). С матрицы предопределенных расчетных коэффициентов 18 соответствующие значения (d, e, f) коэффициентов поступают на соответствующие входы (d, e, f) элементарных расчетных блоков 19, 20, 21, 22, 23. На входы а блоков 19, 20, 21, 22, 23 по магистрали данных 29, соединенной с блоком 11 поступает значение нормировочного коэффициента преобразования. Выходы сумматоров 30 и 31 соединены со входами с и b блоков 19, 20, 21, 22, 23 соответственно. На входы 32, 33 сумматора 30 поступают данные с магистрали 13. Для частного случая косинусного преобразования с шагом перемещения окна преобразования, равного 1, на вход 32 со знаком “+” поступает значение с блока 3 – первого в цепочке из N+2 ячеек памяти 3, 4, 5, 6, 7, 8, 9, 10 буфера FIFO 2, а на вход 33 со знаком “-” поступает значение с блока 4. На входы 34, 35 сумматора 31 поступают данные с магистрали 12. Для рассматриваемого частного случая косинусного преобразования с шагом перемещения окна преобразования, равного 1, на вход 34 со знаком “+” поступает значение с блока 10 – последнего в цепочке из N+2 ячеек памяти 3, 4, 5, 6, 7, 8, 9, 10 буфера FIFO 2, а на вход 35 со знаком “-” поступает значение с блока 9. На фиг. 3 изображена таблица коэффициентов матрицы 18, первая колонка которой содержит последовательные номера вычислительных каскадов (блоки 19, 20, 21, 22, 23), соответствующие порядковым номерам спектральных коэффициентов (от 0 до N-1). Вторая, третья и четвертая колонки таблицы содержат значения коэффициентов, поступающие на соответствующие входы e, f, d каждого вычислительного блока 19, 20, 21, 22, 23. Схема каждого из этих блоков показана на фиг. 4. На умножитель 36 поступают значения со входов c и d. Результат с выхода умножителя 36 поступает со знаком “+” на сумматор 37, в котором это значение суммируется со значением, поступающим со входа b со знаком “+”. Результат суммирования поступает на вход умножителя 38, где он умножается на значения со входов a и e. Полученное произведение с выхода умножителя 38 поступает со знаком “+” на вход сумматора 39. На этот же сумматор со знаком “+” поступает произведение с выхода умножителя 40, который перемножает значения, имеющиеся на входе f и входе буфера FIFO 41, состоящего из двух ячеек памяти 42 (вход) и 43 (выход). Также на сумматор 39 со знаком “-” поступает значение из выходной ячейки 43 буфера 41. Результат суммирования с блока 39 поступает на вход 42 буфера 41, а также на выход g рассматриваемого вычислительного блока.

Способ вычислений, использованный в предложенном устройстве, был реализован практически в виде компьютерной программы. По сравнению с прототипами эта схема вычислений позволила провести сравнительные расчеты, которые могут служить доказательством работоспособности изобретения и его более высокого быстродействия. Таблица результатов этих расчетов приведена на фиг. 5. В качестве анализируемого сигнала была использована первая секунда звучания известного клипа Алана Парсонса “I Am Mirror”, записанная с частотой дискретизации 44100 Гц. Значком в этой таблице обозначено абсолютное среднеквадратичное отклонение спектральных коэффициентов, полученных разными способами, для всего проанализированного участка исходного сигнала.

Изобретение может быть использовано в анализаторах спектра, работающих в реальном масштабе времени, в звуковых процессорах, при цифровой обработке сигналов, компрессии аудиосигналов, контроле технологических процессов и т. д.

Формула изобретения

1. Устройство скользящего ортогонального преобразования сигналов, содержащее входной блок памяти и основной вычислительный блок, отличающееся тем, что в него введен блок нормировочных коэффициентов преобразования, значение сигналов на выходе которого равно 1 для прямого и 2/N для обратного косинусного преобразования, входной блок памяти выполнен в виде буфера FIFO, содержащего N+n+1 ячеек памяти, где n – шаг перемещения окна преобразования, N – размер окна преобразования, причем первая входная ячейка входного блока памяти предназначена для последовательного поступления в нее выборки f_i входного сигнала и сдвига имеющегося значения во вторую входную ячейку памяти и т.д., основной вычислительный блок содержит блок памяти коэффициентов, сумматор, предназначенный для суммирования значений сигналов с первой и второй ячеек входного блока памяти, сумматор, предназначенный для суммирования значений сигналов с предпоследней и последней ячеек входного блока памяти, и арифметические блоки, имеющие входы а, b, с, d, e, f и выход g, причем количество арифметических блоков равно количеству спектральных коэффициентов, входы а арифметических блоков подключены к блоку нормировочных коэффициентов преобразования, входы b арифметических блоков подключены к выходу сумматора, предназначенного для суммирования значений сигналов с предпоследней и последней ячеек входного блока памяти, положительный вход этого сумматора подключен к последней выходной ячейке входного блока памяти, а отрицательный вход этого сумматора подключен к предпоследней выходной ячейке входного блока памяти, входы с арифметических блоков подключены к выходу сумматора, предназначенного для суммирования значений сигналов с первой и второй ячеек входного блока памяти, положительный вход этого сумматора подключен к первой входной ячейке входного блока памяти, а отрицательный выход этого сумматора – к второй входной ячейке входного блока памяти, входы d, e, f арифметических блоков подключены к соответствующим выходам блока памяти коэффициентов, при этом значения коэффициентов на выходе d блока памяти коэффициентов равны (-1)^k, на выходе е блока памяти коэффициентов равны cos(k/2N), на выходе f блока памяти коэффициентов равны 2cos(k/N), где k – порядковый номер спектрального коэффициента и соответствующего ему арифметического блока, при этом каждый арифметический блок содержит умножитель, предназначенный для перемножения сигналов с входов с и d арифметического блока, сумматор, предназначенный для суммирования сигналов с входа b арифметического блока и выхода предыдущего умножителя, умножитель, предназначенный для перемножения сигналов с входов а и е арифметического блока и выхода предыдущего сумматора, буфер FIFO, состоящий из входной и выходной ячеек, умножитель, предназначенный для перемножения сигналов с входа f арифметического блока и входной ячейки буфера FIFO арифметического блока, и сумматор, причем выход умножителя, предназначенного для перемножения сигналов с входов с и d арифметического блока, подключен к положительному входу сумматора, предназначенного для суммирования сигналов с входа b арифметического блока и выхода предыдущего умножителя, другой положительный вход этого сумматора подключен к входу b рассматриваемого арифметического блока, а выход этого сумматора – к входу умножителя, предназначенного для перемножения сигналов с входов a и e арифметического блока и выхода предыдущего сумматора, два других входа этого умножителя подключены к входам a и e арифметического блока, а его выход – к положительному входу сумматора, отрицательный вход которого подключен к выходной ячейке буфера FIFO арифметического блока, третий положительный вход сумматора подключен к выходу умножителя, предназначенного для перемножения сигналов с входа f арифметического блока и входной ячейки буфера FIFO арифметического блока, выход сумматора – к входной ячейке буфера FIFO арифметического блока и к выходу g арифметического блока, выходы g арифметических блоков – к выходам основного вычислительного блока и предназначены для снятия мгновенных значений спектральных коэффициентов а₀, а₁, …, а_k, … а_N-1, соответствующих текущему положению окна анализа, согласно формуле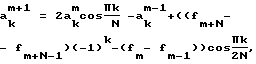

где a_k ^m+1 – очередные значения спектральных коэффициентов;
a_k ^m, a_k ^m-1 – значения спектральных коэффициентов, полученные для предыдущих положений окна преобразования;
m – индекс выборки f_m входного сигнала, поступившей в первую входную ячейку входного блока памяти.

2. Устройство по п.1, отличающееся тем, что N=N(m).

3. Устройство по п.1, отличающееся тем, что N=const.

4. Устройство по п.1, отличающееся тем, что n=n(m).

5. Устройство по п.1, отличающееся тем, что n=const.

РИСУНКИ

MM4A Досрочное прекращение действия патента Российской Федерации на изобретение из-за неуплаты в установленный срок пошлины за поддержание патента в силе

Дата прекращения действия патента: 29.10.2003

Извещение опубликовано: 10.03.2005 БИ: 07/2005