Патент на изобретение №2169940
|
||||||||||||||||||||||||||
(54) СПОСОБ ИЗМЕРЕНИЯ ПЕРЕДАТОЧНОЙ ФУНКЦИИ
(57) Реферат: Изобретение относится к метрологии, а именно к способам (косвенным методам) экспериментальной оценки динамических характеристик средств измерения и элементов систем автоматического управления. Технический результат заключается в повышении точности, оперативности и снижении затрат при измерении передаточных функций объектов. Способ заключается в том, что на вход исследуемого и эталонного объектов одновременно подается одно и то же динамическое воздействие, при этом одновременно фиксируются соответствующие выходные сигналы объектов, которые затем подвергаются преобразованиям Лапласа, после этого находится отношение указанных преобразований и определяется передаточная функция исследуемого объекта как произведение полученного отношения и передаточной функции эталонного объекта. 33 ил. Изобретение относится к метрологии и автоматическому управлению, а именно к способам (косвенным методам) экспериментальной оценки динамических характеристик (ДХ) средств измерений и элементов систем автоматического управления (датчиков). К типовым динамическим характеристикам (функциям), как известно, относятся дифференциальные уравнения, передаточные функции, импульсные переходные характеристики, переходные характеристики, амплитудно-частотные и фазочастотные характеристики. Их взаимосвязь известна: имея одну характеристику, по известным правилам можно найти другую. Поэтому, если будет найдена передаточная функция, то будут найдены и все другие. И в описательной части заявки будем рассматривать косвенные методы измерения той или иной из указанных характеристик, но не обязательно только передаточной функции. Известные косвенные методы измерения динамических характеристик заключаются в нахождении, как правило в аналитической форме, характеристик с помощью известных нехарактеристических испытательных сигналов. В такой ситуации, следуя известной работе [1], можно выделить два случая: испытательный сигнал воспроизводится и повторяется с высокой точностью, тогда соответствующее задающее устройство испытывается и аттестуется как образцовая мера; испытательный сигнал невозможно воспроизводить имеющимися средствами с требуемой точностью, тогда испытательный сигнал при каждом восприятии следует определять и регистрировать с помощью образцовых средств измерений (СИ) достаточно высокой точности. Здесь еще подчеркнем, отмечаемое в указанной работе [1]: оба сигнала – и испытательный (входной) сигнал x(t), и выходной сигнал y(t) должны быть заданы номинальными значениями и нормируемыми характеристиками отклонений от номинальных значений (погрешностей). Подобная задача не всегда оказывается разрешимой. Далее автор [1] утверждает, что при косвенном определении динамических характеристик (ДХ) возникает математическая задача расчета ДХ по известным (номинальным) функциям x(t) и y(t). Математическая формулировка этой задачи зависит от того, какая ДХ подлежит определению. Рассматривая это утверждение как руководство или как рекомендацию в инженерной работе, следует заметить, что оно трудно реализуемо физически или требует значительных затрат при своем выполнении, например импульсное давление можно приближенно задать с помощью сложных ударных труб (УТ-5, НИИФИ, г. Пенза), значения ускорений с помощью сложных и дорогостоящих центрифуг (ДЦ-1, разработки ВНИИМ, г. Санкт-Петербург). Теперь изложим суть известных косвенных методов нахождения оценок динамических характеристик в развернутом виде. При нахождении импульсных переходных функций (ИПФ), а также переходных функций (ПФ) возможны разные подходы к обработке сигналов x(t) и y(t), и зависимости от формы представления последних [1]. Если сигналы x(t) и y(t) можно аппроксимировать некоторыми функциями 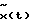 и и 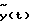 , то потом можно перейти к аналитическому решению известного уравнения в свертках [2]: , то потом можно перейти к аналитическому решению известного уравнения в свертках [2]: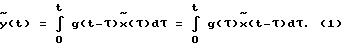 Уравнение (1) можно решать непосредственно прямыми численными методами, что с практической точки зрения более перспективно. Это выглядит следующим образом. С учетом фактической длины отрезка времени, в течение которого регистрируются сигналы (скажем [O, T]), в работе [1] предлагается следующая формулировка последнего выражения: 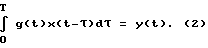 Это интегральное уравнение Фредгольма первого рода с неизвестной функцией g(t). Заменив интеграл суммой, можно получить систему линейных алгебраических уравнений 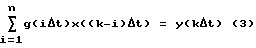 относительно значений искомой импульсной характеристики g(i  t) в дискретные моменты времени i t) в дискретные моменты времени i t. Аналитическое решение может быть получено при определенных аппроксимациях функции x(t).
Известно, что решения интегрального уравнения первого рода некорректные в том смысле, что малые погрешности в определении и регистрации испытательного (входного) и выходного сигналов, т.е. функций x(t) и y(t), приводят к как угодно большим погрешностям определения искомой функции g(t). Последнее свидетельствует о том, что в реальных условиях метод обладает низкой точностью.
Другие известные методы косвенной оценки динамических характеристик в определенной степени подобны изложенному: в каждом предлагаются одновременно известные данные о входном x(t) и выходном y(t) сигналах средств измерения (СИ). К числу этих методов можно отнести: аппроксимативный, алгебраический, метод регуляризации и метод двух взаимосвязанных сигналов.
В случае использования аппроксимативного метода, решение интегрального уравнения [2] с помощью преобразования Фурье дает следующее выражение: t. Аналитическое решение может быть получено при определенных аппроксимациях функции x(t).
Известно, что решения интегрального уравнения первого рода некорректные в том смысле, что малые погрешности в определении и регистрации испытательного (входного) и выходного сигналов, т.е. функций x(t) и y(t), приводят к как угодно большим погрешностям определения искомой функции g(t). Последнее свидетельствует о том, что в реальных условиях метод обладает низкой точностью.
Другие известные методы косвенной оценки динамических характеристик в определенной степени подобны изложенному: в каждом предлагаются одновременно известные данные о входном x(t) и выходном y(t) сигналах средств измерения (СИ). К числу этих методов можно отнести: аппроксимативный, алгебраический, метод регуляризации и метод двух взаимосвязанных сигналов.
В случае использования аппроксимативного метода, решение интегрального уравнения [2] с помощью преобразования Фурье дает следующее выражение: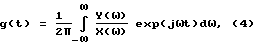 где Y(  ), X( ), X( ) – преобразования Фурье сигналов y(t) и x(t).
g(t) можно вычислять через аппроксимацию спектров Y( ) – преобразования Фурье сигналов y(t) и x(t).
g(t) можно вычислять через аппроксимацию спектров Y( ), Х( ), Х( ) более простыми аналитическими выражениями. Но вся сложность в том, что необходимо знать точное выражение не только выходного (Y(t)), но и входного X(t) сигналов. А это, как уже указывалось выше, в реализации весьма сложная задача: X(t) – может быть импульсом давления, силы, концентрации вещества и т.д., точная их реализация затруднена или невозможна.
Суть алгебраических методов заключается в решении системы алгебраических линейных уравнений [3]. Например, по методу исключения Гаусса. Здесь систему уравнений можно представить в виде, аналогичном (3) ) более простыми аналитическими выражениями. Но вся сложность в том, что необходимо знать точное выражение не только выходного (Y(t)), но и входного X(t) сигналов. А это, как уже указывалось выше, в реализации весьма сложная задача: X(t) – может быть импульсом давления, силы, концентрации вещества и т.д., точная их реализация затруднена или невозможна.
Суть алгебраических методов заключается в решении системы алгебраических линейных уравнений [3]. Например, по методу исключения Гаусса. Здесь систему уравнений можно представить в виде, аналогичном (3)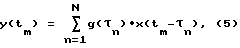 где x(tm –  n ) – значения входного сигнала; g ( n ) – значения входного сигнала; g (  1 ), g 1 ), g  2 ), …, g (tn), …,g( 2 ), …, g (tn), …,g(  N ) – искомые значения весовой функции g(t), y(t1), y(t2),…, y(tm) – известные значения выходного сигнала. Как правило, матрицу x(tm – N ) – искомые значения весовой функции g(t), y(t1), y(t2),…, y(tm) – известные значения выходного сигнала. Как правило, матрицу x(tm –  n ) стремятся свести к так называемой разряженной матрице, у которой немногие элементы отличны от нуля. Это отчасти возможно, если протяженность весовой функции много меньше протяженности анализируемых сигналов. Поэтому каждая неизвестная величина в уравнениях будет связана только с несколькими другими. Для остальных неизвестных коэффициенты x(tm – n ) стремятся свести к так называемой разряженной матрице, у которой немногие элементы отличны от нуля. Это отчасти возможно, если протяженность весовой функции много меньше протяженности анализируемых сигналов. Поэтому каждая неизвестная величина в уравнениях будет связана только с несколькими другими. Для остальных неизвестных коэффициенты x(tm –  n ) в вышеприведенном уравнении будут равны нулю, что существенно снизит точность оценивания g ( n ) в вышеприведенном уравнении будут равны нулю, что существенно снизит точность оценивания g (  ).
Метод регуляризации, носящий имя А.Н.Тихонова, изложен в работе [4]. Он является весьма сложным и громоздким.
В методе регуляризации А.Н.Тихонова ставится задача получения приближенного уравнения Hx = y, устойчивого к малым изменениям правой части, где H – оператор, связывающий входной x и выходной y сигналы. Она решается через нахождение определенных операторов с сопутствующим определением их параметров по дополнительной информации о задаче. Широкого инженерного приложения данный метод не нашел.
Ввиду аналитической и практической проверки на отдельных СИ представляет интерес метод, наиболее близкий к заявляемому, в котором ИПФ определяется по двум реакциям одного устройства при поочередной подаче на его вход двух взаимосвязанных сигналов. Этот метод анализируется в работах [3].
Суть заключается в следующем: на вход линейной системы (объекта), описываемой уравнением ).
Метод регуляризации, носящий имя А.Н.Тихонова, изложен в работе [4]. Он является весьма сложным и громоздким.
В методе регуляризации А.Н.Тихонова ставится задача получения приближенного уравнения Hx = y, устойчивого к малым изменениям правой части, где H – оператор, связывающий входной x и выходной y сигналы. Она решается через нахождение определенных операторов с сопутствующим определением их параметров по дополнительной информации о задаче. Широкого инженерного приложения данный метод не нашел.
Ввиду аналитической и практической проверки на отдельных СИ представляет интерес метод, наиболее близкий к заявляемому, в котором ИПФ определяется по двум реакциям одного устройства при поочередной подаче на его вход двух взаимосвязанных сигналов. Этот метод анализируется в работах [3].
Суть заключается в следующем: на вход линейной системы (объекта), описываемой уравнением 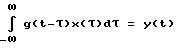 , подаются два сигнала: , подаются два сигнала:x1(t), и 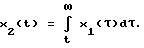 которым соответствуют выходные сигналы 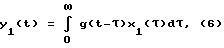 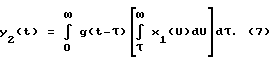 Применив к выражениям (6), (7) преобразование Лапласа (L), получим Y1(S) = G(S)X1(S), 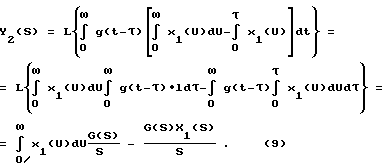 Если далее умножить последнее выражение на S, то получится: 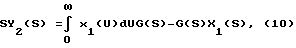 и после несложных преобразований запишется так: 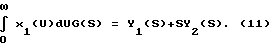 Из выражения (11) находим G(S): 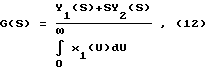 в соответствии с которым 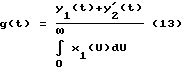 при этом следует иметь в виду, что согласно с [3, 6], y2(0) = 0. Из связи функций g(t) и h(t), с учетом (1), вытекает 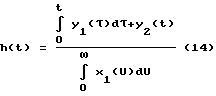 Вычисление ИПФ g(t) по формуле (13) является некорректной задачей, так как таковой является операция дифференцирования [4]. Для ее выполнения необходимо привлекать специальные вычислительные методы [4]. Так для того, чтобы определить функцию g(t) по формуле (13), необходимо замерить значения y1(tk) и y2(tk) в фиксированной системе точек tk, и затем восстановить функцию g(i), пользуясь одним из методов теории приближений (сплайнами, интерполяционными многочленами и т.д.). Но здесь, так же как и в (4), необходимо предварительно знать входное воздействие x(t), да еще интеграл от него, а это уже несет ряд значительных трудностей, указанных выше. Дополнительно к этому еще добавим следующее. Экспериментальная проверка рассматриваемого метода предполагает поочередное прохождение сигналов x1(t) и x2(t) через тракты измерительных и интегрирующих средств. Последнее означает, что соответствующие выходные сигналы будут получены в различных условиях, отличных одно от другого: x1(t) – подается на исследуемое устройство (ИУ) и получается выходной сигнал y1(t), получаемый с погрешностью устройства, его формирующего, подается на интегрирующее устройство, с параметрами и характеристиками, отличными от ИУ. На выходе интегрирующего устройства получается уже сигнал x2(t) который только после этого фиксируется или непосредственно подается на ИУ, которое и выдает выходной сигнал y2(t). Изложенная последовательность действий свидетельствует о весьма длинной цепочке промежуточных преобразований, которая породит дополнительные погрешности в оценках динамических характеристик. Прежде, чем изложить суть предлагаемого способа, кратко подытожим результаты изложенного. Из обзора следует, что для оценок динамических характеристик используются следующие методы: переходных характеристик (ПХ); импульсных переходных (весовых) характеристик (ИПХ); амплитудно-частотных и фазочастотных характеристик (АЧХ, ФЧХ); дифференциальных уравнений. Недостаток первых трех методов состоит в том, что их реализация достаточно трудоемкая и дорогостоящая: требуется специализированное оборудование, указанное выше (например, сложные, очень дорогие и громоздкие центрифуги, ударные трубы, пульсаторы давления и пр.), высококвалифицированный персонал и соответствующие служебные помещения. Для выполнения четвертого метода необходимо знать все динамические процессы, происходящие в тракте СИ, которые не всегда просто выделить, поэтому такой метод часто остается гипотетическим. Цель изобретения – повышение точности, оперативности и снижение затрат при измерении передаточных функций объектов (динамических характеристик). Поставленная цель достигается тем, что на вход исследуемого и эталонного объектов одновременно подается одно и то же динамическое воздействие произвольной формы, при этом одновременно фиксируются соответствующие выходные сигналы объектов, которые затем подвергаются преобразованиям Лапласа, после этого находится отношение указанных преобразований и определяется передаточная функция исследуемого объекта как произведение полученного отношения и передаточной функции эталонного объекта. Кратко изложим суть нового предложенного способа, воспользовавшись схемой одного из устройств, реализующего способ (фиг. 1). В этом устройстве используется парный переходный процесс: это – два переходных процесса, происходящих одновременно в двух различных (приборах, системах) и вызванных одним и тем же испытательным сигналом (входным воздействием). На фиг. 1 имеем: 1 – устройство, формирующее входное воздействие на эталонное средство измерения (СИЭ(2)) и исследуемое (СИИ(3)). Это воздействие для них одновременное, полностью идентичное по причине того, что (1) общее и для (2) и для (3). Цифрами 4 и 5 обозначены регистрирующие средства эталонного и исследуемого, соответственно, СИ, а 6 – устройство, задающее (формирующее) динамические свойства входного воздействия. Для случая, когда СИ (2) и (3) – датчики давления: 1 – баллон, в который нагнетается газ, создающий давление, а 6 – клапан сброса (нагнетания) повышенного давления в баллоне 1. Теперь приведем аналитическое выражение алгоритма, лежащее в основе нового способа 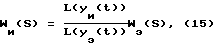 где yИ(t), yэ(t) выходные сигналы исследуемого и эталонного СИ; L(yИ(t)), L(yЭ(t)) – преобразования Лапласа указанных сигналов; WИ(S), Wэ(S) – передаточные функции исследуемого и эталонного СИ. При реализации способа WЭ(S) должна быть известной, yИ(t), yЭ(t) – измеряются и фиксируются в процессе эксперимента, а затем подвергаются преобразованиям Лапласа. WЭ(S) – может быть определена один раз с помощью сложного, дорогого специального оборудования (например, указанного выше), а затем будет многократно использоваться при измерении неизвестных передаточных функций исследуемых объектов. Тем самым дорогое оборудование заменяется несравнимо дешевым эталонным объектом: датчиком, системой или другим средством, которое предварительно аттестовано и поэтому в соответствии с предложенным способом может использоваться для исследований однотипных объектов. Из примера видно, что реализация способа весьма проста: затраты на эксперимент определяются стоимостью устройства, формирующего входное воздействие, и стоимостью регистрирующей аппаратуры. К тому же эксперимент, как видно из примера, может быть воспроизведен в стендовых условиях или непосредственно на месте сборки устройства, т.е. позволяет оперативно получать информацию. Подбирая высокоточные средства регистрации и эталонный объект с точно определенной заранее передаточной функцией, можно определить с достаточной (требуемой) точностью передаточную функцию исследуемого объекта. Также просто можно реализовать эксперимент, например, для определения передаточной функции акселерометра. Для этого исследуемый и эталонный акселерометры необходимо жестко соединить так, чтобы их оси, вдоль которых воздействует ускорение, были параллельны и подвергнуть одновременно их ударной нагрузке и зарегистрировать соответствующие выходные сигналы. При этом точно знать форму и параметры входного воздействия совершенно не обязательно. После этого подвергнуть их обработке в соответствии с (15). Здесь еще раз повторим, что эталонные объекты аттестуются (определяются их передаточные функции) только один раз в специальных лабораторных условиях, т. е. на специальных высокоточных установках, например на прецизионных центрифугах исследуются акселерометры, на специальных ударных трубах или пульсаторах датчики давления и т.д. Стоимость эталонного объекта (акселерометры, датчики давления) в сотни и более раз ниже стоимости ударных труб и центрифуг или других средств аттестации. Этот факт и свидетельствует об экономической выгоде от использования предложенного способа. Метрологические характеристики предложенного способа определяются соответствующими характеристиками эталонного объекта, регистрирующей аппаратурой и точностью обработки полученной информации о выходных сигналах. Необходимая точность эталонного объекта и аппаратуры обеспечивается подбором из числа известных, а точность обработки достигается выбором сплайнов, шага дискретизации информации, длительностью наблюдений выходных сигналов (переходных процессов). Таким образом, по описанному способу определяют передаточные функции, отличающиеся более высокой точностью, малой стоимостью и малым временем на их определение по сравнению с известными способами. Для оценки точности определения динамических характеристик по предложенному способу проводился численный эксперимент, суть которого изложим немного позднее. Вначале выделим, а затем подвергнем экспериментальным исследованиям наиболее весомые особенности способа. К числу требующих исследования особенностей следует отнести: выбор вида сплайнов представления выходных сигналов эталонного и исследуемого объектов, выбор шага дискретизации указанных сигналов и критерия достаточности этого выбора (минимизации шага), а также выбор длительности численного эксперимента в относительных единицах длины фактического эксперимента. С целью оценки точности предложенного способа рассматриваются два вида сплайнов: в виде кусков экспонент и в виде прямоугольных импульсов   0 (t) с амплитудами их значений, равными средним значениям в начале и в конце рассматриваемых участков выходных сигналов объектов (эталонной и исследуемой). В данном случае сплайн 0 (t) с амплитудами их значений, равными средним значениям в начале и в конце рассматриваемых участков выходных сигналов объектов (эталонной и исследуемой). В данном случае сплайн   0 (t) – это полином нулевого порядка, и он является начальной степенью приближения. Другие виды сплайнов в виде хорд или касательных (полиномы первого порядка) могут несколько повысить точность оценок. Они по своему геометрическому смыслу, а значит и по точности приближений, занимают промежуточное положение между экспоненциальными и 0 (t) – это полином нулевого порядка, и он является начальной степенью приближения. Другие виды сплайнов в виде хорд или касательных (полиномы первого порядка) могут несколько повысить точность оценок. Они по своему геометрическому смыслу, а значит и по точности приближений, занимают промежуточное положение между экспоненциальными и   0 (t). В качестве сплайнов могут быть выбраны и полиномы второго порядка (квадратические параболы), и более сложные функции. Но в этом нет жесткой необходимости, по той причине, что применение 0 (t). В качестве сплайнов могут быть выбраны и полиномы второго порядка (квадратические параболы), и более сложные функции. Но в этом нет жесткой необходимости, по той причине, что применение   0 (t) – сплайнов позволяет получить представление о нижней границе точности способа, обусловленной сплайном: погрешности, получаемые в этом случае, будут максимальными. Экспоненциальные сплайны нами рассмотрены потому, что они обеспечивают достаточно высокую точность метода при сравнительной простоте в применении.
Раскроем суть численного эксперимента.
Вначале аналитически определяются точные значения WЭ(S) и WИ(S). Затем с использованием заданного входного воздействия расчетным путем находятся значения (например, в форме таблицы, графика) YИР(t) и YЭР(t). Их преобразования по Лапласу находятся, как уже говорилось, с использованием различного вида сплайнов. На основе получаемых в последнем случае выражений определяется расчетное значение передаточной функции исследуемой системы с учетом формулы 0 (t) – сплайнов позволяет получить представление о нижней границе точности способа, обусловленной сплайном: погрешности, получаемые в этом случае, будут максимальными. Экспоненциальные сплайны нами рассмотрены потому, что они обеспечивают достаточно высокую точность метода при сравнительной простоте в применении.
Раскроем суть численного эксперимента.
Вначале аналитически определяются точные значения WЭ(S) и WИ(S). Затем с использованием заданного входного воздействия расчетным путем находятся значения (например, в форме таблицы, графика) YИР(t) и YЭР(t). Их преобразования по Лапласу находятся, как уже говорилось, с использованием различного вида сплайнов. На основе получаемых в последнем случае выражений определяется расчетное значение передаточной функции исследуемой системы с учетом формулы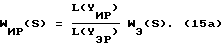 Далее из выражения WИ(S) находятся точные значения АЧХ (AИ) и ФЧХ ( 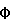 И) исследуемой системы, а из WИР(S) – приближенные (расчетные) значения AИР и И) исследуемой системы, а из WИР(S) – приближенные (расчетные) значения AИР и 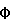 ИP. После этого находятся оценки погрешностей АЧХ и ФЧХ соответственно ИP. После этого находятся оценки погрешностей АЧХ и ФЧХ соответственно AИ= AИР-AИ; (16) AИ= AИР-AИ; (16) 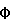 И= И= 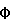 ИР– ИР–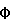 И, (17) И, (17)вызванные использованием данного метода нахождения АЧХ и ФЧХ исследуемой системы (объекта). Поскольку расчетные значения YИР(t), YЭР(t) и их преобразования оцениваются с конечной точностью, погрешности (16) и (17) будут иметь конечные значения, которые будут изменяться наряду с изменением шага квантования (дискретизации) выходных сигналов, а также с изменением вида используемых сплайнов. Теперь конкретизируем изложенный эксперимент применительно, например, к динамической системе второго порядка. Так при воздействии   0 (t) сигнала на систему указанного порядка, которая описывается уравнением 0 (t) сигнала на систему указанного порядка, которая описывается уравнением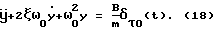 где 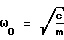 – собственная частота (круговая) системы; – собственная частота (круговая) системы;c – жесткость (подвесов) системы; m – масса подвижной части системы; 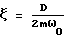 – степень успокоения системы – безразмерная величина; – степень успокоения системы – безразмерная величина;D – коэффициент демпфирования системы; B – амплитуда импульсного воздействия на систему, аналитическое выражение выходного сигнала системы имеет вид 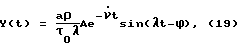 где 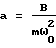 ; ; 0 – длительность 0 – длительность   0 (t) – функции сигнала, воздействующего одновременно на обе системы (эталонную и исследуемую); 0 (t) – функции сигнала, воздействующего одновременно на обе системы (эталонную и исследуемую);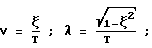 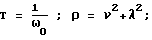 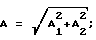 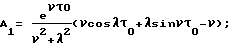 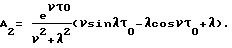 Произведем расчет выходных сигналов систем YЭ(t) и YИ(t) по формуле (19), т.е. найдем частные решения уравнения (18). В качестве систем выберем два акселерометра при следующих числовых данных:  0 = 0,05 с; 0 = 0,05 с;  = 0,75; m = 0,022 кг; = 0,75; m = 0,022 кг;  0 = 95 рад/с; B = 0,2H для одной системы и при 0 = 95 рад/с; B = 0,2H для одной системы и при  0 = 0,05 с; 0 = 0,05 с;  = 0,7; m = 0,02 кг; = 0,7; m = 0,02 кг;  0 = 100 рад/с; B = 0,2H для другой системы (их смысл можно менять: эталонная, исследуемая и наоборот). Выходные сигналы представляются графиками “0” и “1” на фиг. 2 соответственно.
Теперь далее будем использовать эти данные и выражение L( 0 = 100 рад/с; B = 0,2H для другой системы (их смысл можно менять: эталонная, исследуемая и наоборот). Выходные сигналы представляются графиками “0” и “1” на фиг. 2 соответственно.
Теперь далее будем использовать эти данные и выражение L( (t)) со сплайнами в виде ансамблей экспонент, где (t)) со сплайнами в виде ансамблей экспонент, где 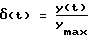 – нормированный выходной сигнал.
Преобразование по Лапласу сигнала вида фиг. 2 и выраженного экспоненциальными сплайнами, можно представить так – нормированный выходной сигнал.
Преобразование по Лапласу сигнала вида фиг. 2 и выраженного экспоненциальными сплайнами, можно представить так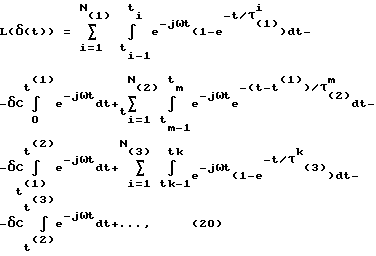 где  C – относительное смещение сигнала в область положительных значений: C – относительное смещение сигнала в область положительных значений:обеспечивает возможность использования сплайнов экспонент. Взяв интегралы и подставив пределы, произведем элементарные преобразования, используя формулы Эйлера для комплексных чисел, с целью разделить выражение на действительную и мнимую части. После дополнительных элементарных преобразований легко представить выражение (20) в виде суммы действительной и мнимой частей (для последующей оценки АЧХ и ФЧХ) L( 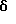 (t)) = A1 + jB1, (21) (t)) = A1 + jB1, (21)где A1 имеет следующий конкретный вид 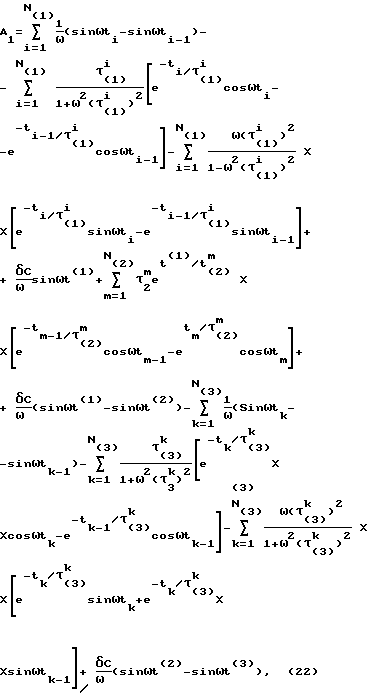 а B1 – следующий вид 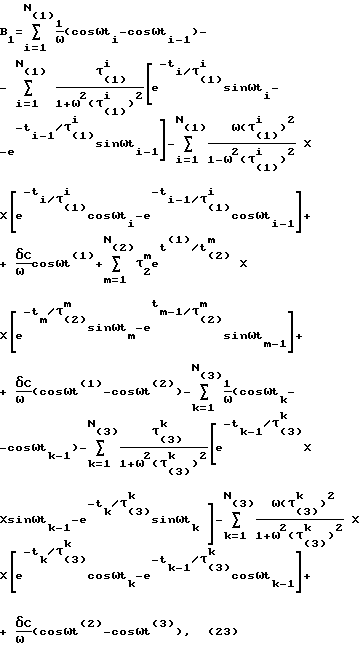 Оценки АЧХ и ФЧХ запишутся так 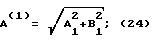 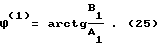 Далее для сравнения рассмотрим случай, когда в качестве сплайнов использовались   (t) функции.
В общем случае преобразования по Лапласу таким образом представленного сигнала в частотном виде имеет вид (t) функции.
В общем случае преобразования по Лапласу таким образом представленного сигнала в частотном виде имеет вид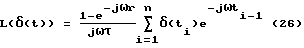 После преобразований, подобных вышеуказанным, будем иметь L ( 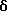 (t)) = A2 + jB2; (27) (t)) = A2 + jB2; (27)где A2 имеет следующий конкретный вид 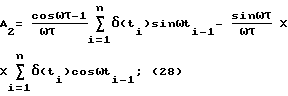 а B2 – следующий вид 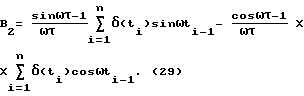 В последних выражениях 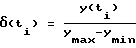  – шаг дискретизации сигнала по времени (t1 – ti-1 = – шаг дискретизации сигнала по времени (t1 – ti-1 =  ); );n – число контролируемых точек на кривой сигнала. Отсюда 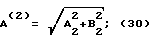 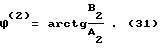 Сравнивая результаты расчетов по формулам (25), (26) и (30), (31), можно оценить относительную точность (приближение) расчетных характеристик к теоретическим точным. Результаты расчетов представлены на чертежах. На чертежах АЧХ точные (1) и расчетные (2) системы с индексом “0” обозначены соответственно AОТ, AОР, систем с индексом “1” – A1Т, A1Р; ФЧХ обозначены  с необходимыми пояснениями. Далее рассмотрим последовательно все результаты численного эксперимента и расчетов на его основе АЧХ и ФЧХ, представленных в табл. 1-4 фиг. 3-33.
Вначале рассмотрим расчеты и их результаты, полученные с использованием с необходимыми пояснениями. Далее рассмотрим последовательно все результаты численного эксперимента и расчетов на его основе АЧХ и ФЧХ, представленных в табл. 1-4 фиг. 3-33.
Вначале рассмотрим расчеты и их результаты, полученные с использованием   0 (t) сплайнов, как наиболее простые, а затем – результаты, полученные с использованием экспоненциальных сплайнов.
На фиг. 3 (табл. 1) представлен график точной АЧХ системы, полученной расчетным путем, исходя из точного выражения ее передаточной функции 0 (t) сплайнов, как наиболее простые, а затем – результаты, полученные с использованием экспоненциальных сплайнов.
На фиг. 3 (табл. 1) представлен график точной АЧХ системы, полученной расчетным путем, исходя из точного выражения ее передаточной функции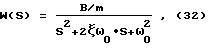 при значении параметров, указанных для системы “0”, и график приближенной АЧХ той же системы “0”, полученный расчетным путем с учетом формулы (15а). В этом случае система “1” играла роль эталонной. АЧХ представлены в абсолютных единицах [мкм]: Y – прогиб подвесов систем [мкм]. На фиг. 4 представлены графики относительных погрешностей (усредненной и не усредненной) оценки АЧХ, полученной расчетным путем с использованием выражения (18). Погрешность относительная усредненная представлена на фиг. 4 графиком 1. Погрешность относительная без усреднения (без сглаживания) определена по формуле 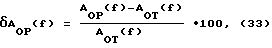 где AОТ(f) – точное значение АЧХ системы “0”; AОР(f) – расчетное значение АЧХ системы “0”, и представлена графиком 2 на фиг. 4. На фиг. 5 представлен график точной АЧХ системы “1” полученной также расчетным путем на основании формулы (32) при значениях параметров, указанных для системы “1”, и график приближенной АЧХ той же системы “1”, полученный расчетным путем по формуле (15а). На фиг. 6 показаны графики погрешностей АЧХ, полученных расчетным путем, по аналогии с вышеизложенным. В данном случае система “0” играла роль эталонной. Погрешности оценивались по формуле, аналогичной (33) 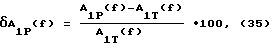 где A1Т(f) – точное значение АЧХ системы “1”; A1Р(f) – расчетное значение АЧХ системы “1”. На фиг. 7 изображены графики ФЧХ для систем “0” и “1”. При этом оказалось, что расчетные и точные значения ФЧХ очень близки и на графиках неразличимы, т.е. предложенный метод позволяет достаточно точно определять ФЧХ систем на основе парных переходных процессов. Аналогичные расчеты были произведены для оценки характеристик систем “0” и “1” при использовании сплайнов в виде ансамблей экспонент. Результаты расчетов представлены на фиг. 8-12 (табл.1). Из анализа и сравнения графиков фиг. 3 и фиг. 8, фиг. 5 и фиг. 10 видно, что характер поведения точной и расчетной АЧХ в зависимости от f (частоты) достаточно близки и повторяют друг друга. Из сравнения графиков фиг. 6 и фиг. 11 видно, что экспоненциальные сплайны обеспечивают более высокую точность, чем   0 (t) сплайн (особенно в области низких частот). Поэтому более высокая трудоемкость расчетов при экспоненциальных сплайнах, вызванная сложностью аналитических выражений, окупается снижением погрешностей оценок АЧХ. Но при этом следует отметить, что указанное снижение погрешностей не столь существенно и в инженерной практике в неответственных случаях следует пользоваться 0 (t) сплайн (особенно в области низких частот). Поэтому более высокая трудоемкость расчетов при экспоненциальных сплайнах, вызванная сложностью аналитических выражений, окупается снижением погрешностей оценок АЧХ. Но при этом следует отметить, что указанное снижение погрешностей не столь существенно и в инженерной практике в неответственных случаях следует пользоваться   0 (t) сплайнами.
При изменении длительности эксперимента (при цензурировании данных, представленных на фиг.2) все рассмотренные оценки характеристик также подверглись измерениям.
Так при цензурировании данных с 0,08 с (фиг. 1) до 0,04 с (фиг. 13) (табл. 2) расхождение АЧХ расчетной (2) и точной (1) для системы с индексом “0” стало существенным (фиг. 14), на фиг. 15 график погрешности, определенной по формуле (33). На фиг. 16 графики АЧХ расчетной (2) и точной (1), на фиг. 17 – график погрешности, определенной по формуле (34). На фиг. 18 графики (1) ФЧХ системы с индексом “0”, графики (2) ФЧХ системы с индексом “1”. Из этих графиков видно, что при малой продолжительности исходных данных (продолжительность сокращена в 2 раза) заметно увеличение всех погрешностей.
При увеличении продолжительности с 0,04 с до 0,06 с указанные погрешности сокращаются в 3 и более раз.
Все представленные выше результаты расчетов были выполнены с шагом дискретизации данных во времени 0 (t) сплайнами.
При изменении длительности эксперимента (при цензурировании данных, представленных на фиг.2) все рассмотренные оценки характеристик также подверглись измерениям.
Так при цензурировании данных с 0,08 с (фиг. 1) до 0,04 с (фиг. 13) (табл. 2) расхождение АЧХ расчетной (2) и точной (1) для системы с индексом “0” стало существенным (фиг. 14), на фиг. 15 график погрешности, определенной по формуле (33). На фиг. 16 графики АЧХ расчетной (2) и точной (1), на фиг. 17 – график погрешности, определенной по формуле (34). На фиг. 18 графики (1) ФЧХ системы с индексом “0”, графики (2) ФЧХ системы с индексом “1”. Из этих графиков видно, что при малой продолжительности исходных данных (продолжительность сокращена в 2 раза) заметно увеличение всех погрешностей.
При увеличении продолжительности с 0,04 с до 0,06 с указанные погрешности сокращаются в 3 и более раз.
Все представленные выше результаты расчетов были выполнены с шагом дискретизации данных во времени  t = 0,0001 с и повторены далее с шагом t = 0,0001 с и повторены далее с шагом  t = 0,001 с; 0,005 с; 0,01 с.
Для этих случаев результаты расчетов АЧХ и ФЧХ, погрешностей АЧХ и ФЧХ представлены на фиг. 19-33 (табл. 3, 4).
Из графиков указанных чертежей видно, что с увеличением шага дискретизации погрешность оценки АЧХ растет более заметно, чем погрешность ФЧХ. Так при шаге t = 0,001 с; 0,005 с; 0,01 с.
Для этих случаев результаты расчетов АЧХ и ФЧХ, погрешностей АЧХ и ФЧХ представлены на фиг. 19-33 (табл. 3, 4).
Из графиков указанных чертежей видно, что с увеличением шага дискретизации погрешность оценки АЧХ растет более заметно, чем погрешность ФЧХ. Так при шаге  t = 0,001 с погрешности АЧХ несколько увеличились (фиг. 19-22, в табл. 3), а при шаге t = 0,001 с погрешности АЧХ несколько увеличились (фиг. 19-22, в табл. 3), а при шаге  t = 0,005 с эти же погрешности возросли более чем в 3 раза (фиг. 24-27), а при шаге 0,01 с – почти на порядок (фиг. 29-32, в табл. 4), погрешности ФЧХ возрастали медленно и их заметное проявление оказалось только при шаге 0,01 с (фиг. 23, фиг. 28, фиг. 33). При исследовании влияния шага дискретизации использовались t = 0,005 с эти же погрешности возросли более чем в 3 раза (фиг. 24-27), а при шаге 0,01 с – почти на порядок (фиг. 29-32, в табл. 4), погрешности ФЧХ возрастали медленно и их заметное проявление оказалось только при шаге 0,01 с (фиг. 23, фиг. 28, фиг. 33). При исследовании влияния шага дискретизации использовались   0 (t) сплайны.
Технические преимущества заявляемого способа по сравнению с прототипом [3, 5] заключаются в возможности повышения точности с одновременным упрощением процедур измерения динамических характеристик, т.е. повышении оперативности, снижении затрат на их проведение.
Предложенный способ прост в реализации, а поэтому для ряда объектов может быть реализован на стендах, на предприятиях, в полевых условиях. Это позволяет повысить оперативность получения информации, ее уточнение в реальных условиях применения объектов при существенно низких затратах по сравнению с прототипами.
Таким образом, предложенный способ более чувствителен к длительности эксперимента (цензурированию данных), менее чувствителен к виду используемых сплайнов (из числа рассмотренных) и достаточно чувствителен к вариации (на порядок) шага дискретизации выходных сигналов систем.
Из приведенных данных следует, что предложенный способ обеспечивает высокие метрологические характеристики, которые могут регулироваться выбором таких параметров, как шаг дискретизации данных, длительность эксперимента, и выбором сплайнов аппроксимации.
Источники информации 0 (t) сплайны.
Технические преимущества заявляемого способа по сравнению с прототипом [3, 5] заключаются в возможности повышения точности с одновременным упрощением процедур измерения динамических характеристик, т.е. повышении оперативности, снижении затрат на их проведение.
Предложенный способ прост в реализации, а поэтому для ряда объектов может быть реализован на стендах, на предприятиях, в полевых условиях. Это позволяет повысить оперативность получения информации, ее уточнение в реальных условиях применения объектов при существенно низких затратах по сравнению с прототипами.
Таким образом, предложенный способ более чувствителен к длительности эксперимента (цензурированию данных), менее чувствителен к виду используемых сплайнов (из числа рассмотренных) и достаточно чувствителен к вариации (на порядок) шага дискретизации выходных сигналов систем.
Из приведенных данных следует, что предложенный способ обеспечивает высокие метрологические характеристики, которые могут регулироваться выбором таких параметров, как шаг дискретизации данных, длительность эксперимента, и выбором сплайнов аппроксимации.
Источники информации1. Челпанов И.Б. Состояние и задачи метрологии динамических измерений. Современные проблемы метрологии в системе метрологического обеспечения. Межвузовский сборник научных трудов. Всесоюзный заочный машиностроительный институт. Москва, 1985, с. 12-23. 2. Азизов А.М., Гордов А.Н. Точность измерительных преобразователей. – Л.: Энергия. – 1975. – 256 с. 3. Черушева Т. В. Методы определения динамических характеристик. Диссертация на соискание ученой степени кандидата технических наук. Специальность 05.11.05. – “Приборы и методы измерения электрических и магнитных величин”. Пензенский государственный технический университет, Пенза, 1997. 4. Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. – М.: Наука.- 1986. – 223 с. 6. Ланцош К. Практические методы прикладного анализа. – М.: ГИФМЛ. – 1961. – 51 с. Формула изобретения
РИСУНКИ
MM4A Досрочное прекращение действия патента Российской Федерации на изобретение из-за неуплаты в установленный срок пошлины за поддержание патента в силе
Дата прекращения действия патента: 27.10.2002
Номер и год публикации бюллетеня: 10-2004
Извещение опубликовано: 10.04.2004
|
||||||||||||||||||||||||||
