Патент на изобретение №2399060

(54) СПОСОБ АНАЛИЗА МНОГОЧАСТОТНЫХ СИГНАЛОВ, СОДЕРЖАЩИХ СКРЫТЫЕ ПЕРИОДИЧНОСТИ

(57) Реферат:

Изобретение относится к области обработки информации и измерительной техники, может быть использовано при контроле электротехнических и электромеханических устройств. Способ анализа сигналов выполняют с использованием непрерывных цепных С-дробей путем измерения сигнала в равноотстоящие промежутки времени. Сигнал подают с датчика анализируемых сигналов (ДАС) контролирующего устройства в блок 1 – идентификатор непрерывной цепной С-дроби, в котором последовательно проводят обработку значения сигнала х(k) по формуле: 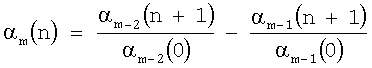до выполнения правила останова, где _-1(n)=(n) – дельта функция Дирака, ₀(n)=x(n) – измерения сигнала, m=1,2,3,, n=0,1,2,, с последующим восстановлением прогнозирующей модели сигнала в форме скрытой периодичности. Технический результат заключается в упрощении и ускорении процессов анализа, диагностики, контроля и управления. 4 ил., 4 табл.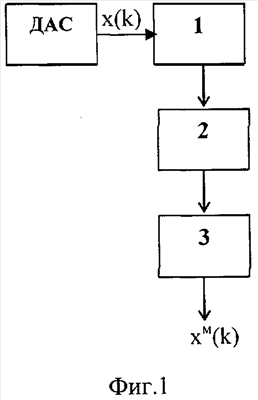

Изобретение относится к области обработки информации и измерительной техники и может быть использовано для контроля работоспособности электротехнических и электромеханических устройств. Способ может быть применен для определения математической модели детерминированного сигнала, обладающего определенной периодичностью, на основе дискретной информации о нем, и реализован с использованием ЭВМ в автоматическом режиме, в реальном масштабе времени.

Известен способ спектрального анализа периодических многочастотных сигналов (патент РФ 2335778, МПК G01R 23/16, опубл. 2008.10.10), основанный на определении мгновенной спектральной плотности для последовательности частот. Затем определяют экстремумы характеристики распределения мгновенной спектральной плотности, по которым определяют частоты и далее амплитуды, для определения фазы формируют опорный синусоидальный сигнал, строят вольт-амперную характеристику для исходного сигнала, многократно сдвигают ее по фазе, определяя площадь вольт-амперной характеристики F_BAX, фазу каждой частотной составляющей сигнала находят из условия F_BAX=0. Далее по полученным значениям амплитуд, круговых частот и фаз судят о спектральном составе исходного сигнала.

Данный способ имеет следующие недостатки, снижающие быстродействие и точность метода:

– громоздкость и неточность метода Фурье при расчете спектральной плотности;

– необходимость процедуры перебора фаз и частот при оценке параметров сигнала;

– для реализации метода необходимы большое количество измерений сигнала (порядка 10000) и малый шаг дискретизации (порядка 10^-4).

Известен способ спектрального анализа сигналов (патент РФ 2229139, МПК G01R 23/16, опубл. 2004.05.20), основанный на перемножении опорного бинарного зондирующего и анализируемого сигналов, суммировании полученных значений за период анализируемого сигнала и расчете постоянной составляющей произведения опорного и анализируемого сигналов на каждой частоте опорного сигнала при переборе фазы опорного сигнала от 0 до 180°. По максимуму постоянной составляющей произведения сигналов определяют частоту и фазу гармонической составляющей анализируемого сигнала, а также рассчитывают ее амплитуду.

Данный способ имеет следующие недостатки, снижающие быстродействие и точность метода:

– громоздкость и неточность метода Фурье при расчете спектральной плотности;

– процедура перебора фазы опорного сигнала;

– для реализации метода необходимы большое количество измерений сигнала (более 200) и малый шаг дискретизации (меньше либо равен 10^-3).

Известен способ спектрального анализа сигналов (патент РФ 2229140, МПК G01R 23/16, опубл. 2004.05.20), основанный на перемножении анализируемого сигнала и опорных синусоидальных и косинусоидальных сигналов. Суммируют полученные значения на интервале Т_И анализируемого сигнала и рассчитывают мгновенную спектральную плотность на каждой частоте. Затем рассчитывают амплитудное значение и фазовый угол каждой гармонической составляющей.

Данный способ имеет следующие недостатки, снижающие быстродействие и точность метода:

– громоздкость и неточность метода Фурье при расчете спектральной плотности;

– для реализации метода необходимо большое количество измерений сигнала (более 200) и малый шаг дискретизации (меньше либо равен 10^-3);

– необходимость перебора круговых частот опорного сигнала, производящаяся до появления соответствия с частотами анализируемого сигнала.

Наиболее близким к предлагаемому способу является способ выявления срытых периодичностей сигнала на основе непрерывных цепных дробей (Серебренников М.Г., Первозванский А.А. Выявление скрытых периодичностей. – М.: Наука, 1965), сущность которого состоит в следующем. Последовательность результатов измерений сигнала в равноотстоящие промежутки времени делят пополам

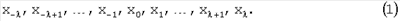
Далее записывают эту последовательность в обратном порядке, причем числа, стоящие в первых столбцах, складывают, а стоящие в следующих столбцах – вычитают. В результате получаются коэффициенты непрерывных цепных дробей, используемые для построения рекуррентных рядов S₁ и S₂, причем коэффициенты первой серии должны быть взяты справа налево, а второй серии – слева направо. Ряд S₁

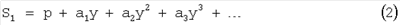
делят на p, в результате имеют ряд S. После этого делят 1-у на ряд S, чтобы образовалось частное вида 1+у²+qy и остаток вида

Если коэффициенты первого остатка не малы, то его необходимо разделить на p’y². Полученный ряд обозначают S’. Далее, деля S на S’ так, чтобы частное имело вид 1+у+q’y, получают второй остаток. Если остаток равен нулю, то действия считаются законченными, в противном случае – процесс деления продолжается (число гармоник процесса n равно числу делений). В результате получаются последовательности величин р, р’, р”, и q, q’, q”,.

Поступая с рядом S₂ так же, как указано для S₁, следует в качестве первого делимого взять 1+у. В результате получаются последовательности величин (p), (p’), (p”), и (q), (q’), (q”),

Преобразуя р, р’, р”,, q, q’, q”,, (р), (р’), (р”), и (q), (q’), (q”), в зависимости от числа выявленных гармоник, находят модель сигнала в виде скрытых периодичностей:

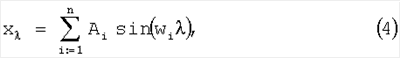
где A_i – амплитуда i-й гармоники, w_i – круговая частота i-й гармоники. Причем для нахождения круговых частот достаточно воспользоваться только рядом S₁ или S₂, а для получения амплитуд необходимо пользоваться двумя рядами.

Этот способ имеет следующие недостатки:

– итерационная процедура определения модели сигнала на основе перебора непрерывных цепных дробей требует выполнения значительного числа операций, что снижает быстродействие и точность расчетов;

– наличие областей неопределенности при нахождении параметров гармоник приводит к невозможности получения модели сигнала.

Предлагаемым изобретением ставится задача выявления скрытых периодичностей многочастотного сигнала, позволяющая автоматически определить структуру и неизвестные параметры математической модели сигнала, исключая итерационную процедуру корректировки модели сигнала на основе перебора непрерывных цепных дробей, значительным образом упрощая и ускоряя процесс получения модели сигнала, что дает возможность использовать данный метод в реальном масштабе времени, контролировать изменения структуры и параметров модели и тем самым повышать точность и достоверность результатов моделирования.

Предлагаемый способ выявления скрытых периодичностей обладает рядом преимуществ, которые выражаются в том, что обеспечивается быстродействие, универсальность реализации способа, простота и высокая точность вычислений.

Способ анализа многочастотных сигналов, содержащих скрытые периодичности, с использованием непрерывных цепных дробей путем измерения сигнала в равноотстоящие промежутки времени, отличается тем, что сигнал подают с датчика анализируемых сигналов в идентификатор непрерывной цепной С-дроби, в котором последовательно проводят обработку значений сигнала по формуле

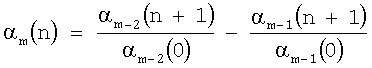
до выполнения правила останова, где _-1(n)=(n) – дельта функция Дирака, ₀(n)=x(n) – измерения сигнала, m=1, 2, 3,, n=0, 1, 2, с последующим восстановлением прогнозирующей модели сигнала в форме скрытой периодичности.

Изобретение поясняется на фигурах 1-4.

Структурная схема системы, изображенная на фиг.1 и реализующая предлагаемый способ, содержит датчик анализируемого сигнала (ДАС), к которому последовательно подсоединены блок 1 – идентификатор непрерывной цепной С-дроби, блок 2 – восстановитель модели сигнала, блок 3 – восстановитель модельных значений сигнала.

С выхода ДАС анализируемый сигнал x(k) поступает на вход блока 1 – идентификатора непрерывной цепной С-дроби. В блоке 1 рассчитывается идентифицирующая матрица (5), то есть производится последовательная обработка значений сигнала с помощью формулы (6) до выполнения правила останова, строится непрерывная цепная С-дробь и определяется модель сигнала в форме дискретной передаточной функции (ДПФ) формирующего объекта. Далее в блоке 2 -восстановителя модели сигнала – определяют параметры сигнала (круговые частоты, амплитуды) и его прогнозирующую модель, по которой судят о наличии скрытых периодичностей сигнала. Затем прогнозирующая модель поступает на вход блока 3 -восстановителя модельных значений сигнала, в котором определяется модельный сигнал х^м (k).

Предлагаемый способ осуществляется следующим образом: с ДАС результаты измерений сигнала в равноотстоящие промежутки времени с шагом дискретизации t поступают на вход блока 1, где рассчитывается идентифицирующая матрица:

,

где элементы _m(nt) последовательно определяются с помощью формулы

причем _-1(nt)=(nt), ₀(nt)=x(nt) являются начальными условиями при построении матрицы, где (t) – дельта функция Дирака, m=1, 2, 3,, n=0, 1, 2,.

Элементы первого столбца идентифицирующей матрицы (5) порождают непрерывную цепную С-дробь

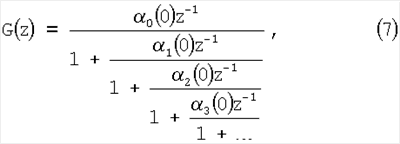
сворачивая которую, определяют модель формирующего объекта в форме ДПФ.

При аппроксимации дробно-рациональной функции в матрице (5) наблюдается появление нулевой строки, номер которой позволяет определить число периодических компонент. А именно, если в идентифицирующей матрице j-я строка является нулевой, то число периодических компонент в сигнале равно .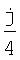

Если в некоторой i-той строке (i=0, 1, 2,) матрицы (5) конечное число k_i первых элементов равно нулю, а последующие элементы отличны от нуля, то необходимо осуществить сдвиг влево на k_i элементов до появления в нулевом столбце ненулевого элемента и далее продолжить определение других элементов матрицы (5) по формуле (6). Для i-той строки при восстановлении непрерывной С-дроби (7) элемент _i (0) умножается на .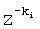

Полученная ДПФ (7) поступает на вход блока 2, в котором определяются параметры гармоник – круговые частоты и амплитуды. Для этого определяются полюса ДПФ z_i. Если ДПФ содержит только комплексные полюса, то сигнал является периодическим или почти периодическим. В случае наличия комплексных полюсов приступают к нахождению круговых частот w_i из выражения

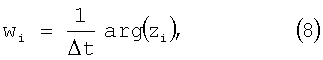
где z_i=u+iv – полюса ДПФ.

Амплитуды находятся как решение системы из n уравнений

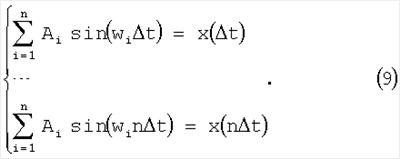
На вход блока 3 прогнозирующая модель сигнала поступает в виде скрытых периодичностей:

Таким образом, предлагаемый способ анализа многочастотных сигналов, содержащих скрытые периодичности, отличается от известного тем, что используют последовательную процедуру выполнения операций и математическую формулу вида (6), которые позволяют автоматически определять количество и параметры скрытых периодичностей сигнала, исключая итерационную процедуру определения математической модели сигнала на основе перебора непрерывных цепных дробей. Способ позволяет выявлять наличие скрытых периодичностей для большего класса сигналов (периодических и почти периодических) на основе минимального количества наблюдений. Предлагаемый способ приводит к существенному упрощению и ускорению процесса выявления скрытых периодичностей за счет исключения большого объема вычислительных операций, что позволяет в конечном итоге достоверно прогнозировать значения физического процесса, принимать адекватные решения по его контролю, управлению и диагностике.

Пример 1.

Вибрация многомоторного винтового самолета с несинхронизированными двигателями описывается с помощью модели почти периодического сигнала

.

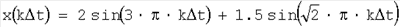С ДАС на вход блока 1 – идентификатора непрерывной цепной С-дроби – поступают значения сигнала с шагом дискретизации t=0.1, k=0,1,2,. График сигнала приведен на фиг.2. В блоке 1 измерения преобразовываются в непрерывную дробь путем расчета идентифицирующей матрицы на основе формулы (6)

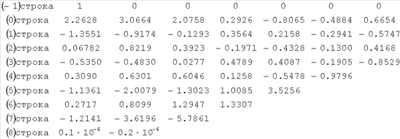
Восьмая строка нулевая. Число периодических компонент в сигнале равно 8/4=2. Модель сигнала в форме ДПФ на выходе блока 1 имеет вид

.

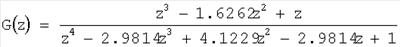Блок 2 – восстановитель модели определяет ее полюса, круговые частоты и амплитуды:

,

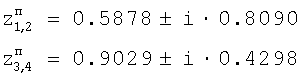w₁=9.4248, w₂=4.4429,

A₁=2,

A₂=1.5.

На выходе блока 2 снимают прогнозирующую модель, содержащую две скрытых периодичности:

х^м(kt)=2sin(9.4348 kt)+1.5sin(4.4429 kt)

и передают ее на вход блока 3 – восстановителя модельных значений сигнала, на выходе которого снимают модельный сигнал х^м(k). Результаты вычислений приведены в Табл.1, где х^м(kt) – модельные значения сигнала, рассчитанные с помощью предлагаемого способа, e(kt)=x(kt)-х^м(kt) – погрешности модельных значений.

Таким образом, по предлагаемому способу точно восстановлена прогнозирующая модель сигнала, что в конечном итоге позволяет получить наилучший прогноз значений сигнала вибрации многомоторного винтового самолета и определить его скрытые периодичности.

Пример 2.

Измерения многочастотного сигнала напряжения на выходе электрического генератора с шагом t=0.001 (график сигнала приведен на фиг.3)

x(kt)=4sin(300··kt)+2sin(200··kt)+sin(380··kt) поступают с ДАС на вход блока 1, в котором рассчитывается идентифицирующая матрица. Двенадцатая строка в матрице нулевая, число периодических компонент сигнала равно 3. Модель формирующего объекта в форме ДПФ снимают на выходе блока 1

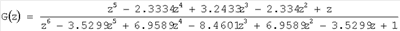
и передают на вход блока 2 – восстановителя прогнозирующей модели сигнала, в котором определяются круговые частоты

w₁=1193.804, w₂=942.477, w₃=628.319

и амплитуды как решение системы уравнений:

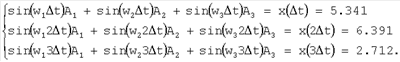
На выходе блока 2 прогнозирующая модель с 3-мя скрытыми гармониками имеет вид:

х^м(kt)=sin(1193.804kt)+4sin(942.477kt)+1.999sin(628.319kt).

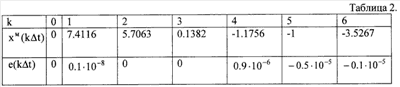
Результаты вычислений модельного сигнала напряжения на выходе блока 3 приведены в Табл.2, где х^м(kt) – модельные значения сигнала, рассчитанные с помощью предлагаемого способа, e(kt)=x(kt)-х^м(kt) – погрешности модельных значений. Сравнение экспериментальных и модельных значений сигнала напряжения позволяет сделать заключение о точном (с точностью до вычислительных погрешностей) модельном его восстановлении.

Пример 3.

Сравнительный анализ предлагаемого способа с прототипом.

Имеются измерения анализируемого сигнала по прототипу, например электрического тока в цепи питания

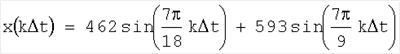
с шагом дискретизации t=1, k=0,,9 (график сигнала приведен на фиг.4). Были сняты десять наблюдений сигнала k=0,9 (таблица 3, 1-й столбец). В качестве x₀ выбирается величина, равная x₄=-657.79913. Далее записывается последовательность из тех же чисел, но в обратном порядке. Затем первые пять чисел складывались, а следующие пять – вычитались. В результате получились коэффициенты непрерывных цепных дробей, значения которых приведены в 2-м столбце Табл.3, причем коэффициенты первой серии должны быть взяты в обратном порядке, а второй серии – в порядке следования. Тогда ряд S₁ имеет вид

S₁=-940.8425+1196.2099у – 517.1016у²+1038.4708у³+

В результате деления S₁ на р=-940.8425 получается ряд

S=1-1.2714у+0.5496у²-1.1038у³+

Деля 1-у на ряд S, рассчитывается частное

1+у²+0.2714у,

так что q=0.2714, а первый остаток от деления равен

-1.2045у²+2.2260у³-0.7411у⁴+,

откуда р’=-1.2045. Так как коэффициенты первого остатка не малы, то следует продолжать действие дальше.

Производится деление всех членов первого остатка на р’у²

S’=1-1.8480у+0.6152у²-0.8057у³+

Деля S на S’ так, чтобы частное имело вид 1+у²+q’у, рассчитывается второе частное 1+у²+0.5766у, а второй остаток

1.1952у³-0.0673у⁴+0.5706у⁵+

Коэффициенты остатка не равны нулю, процесс деления должен продолжаться. Однако, согласно алгоритму, число скрытых периодичностей процесса n равно числу делений, следовательно, количество данных не достаточно для выявления скрытых периодичностей.

Были сняты двадцать наблюдений сигнала N=0,19 (Табл.3, 3-й столбец). В качестве x₀ выбирается величина, равная x₉=-462. Рассчитываются коэффициенты непрерывных цепных дробей первой и второй серии (4-й столбец Табл.3). Используя коэффициенты первой серии, составляется ряд S₁, который делится на р=-1001.1864, и получается ряд

S=1-1.1597у+0.3431у²-1.0350у³+

Деля 1-у на ряд S, рассчитывается частное

1+у²+0.1597у,

так что q=0.1597, а первый остаток от деления равен

-1.1579у²+2.1399у³-0.7124у⁴+,

откуда р’=-1.1579.

Так как коэффициенты первого остатка не малы, то следует продолжать действие дальше. Производится деление всех членов первого остатка на р’у²:

S’=1-1.8480у+0.6152у²+0.3895у³+

Деля S на S’, получается второе частное 1+у²+0.6884у, второй остаток равен нулю. Для ряда S₂ используются коэффициенты второй серии:

S₂=-77.1864+714.7438у+116.6291у²-791.0643у³+

Так как р=-77.1864, то

S=1-9.2600у-1.5110у²+10.2488y³+

Результатом деления 1+у на ряд S является частное

1+у²+10.2600у,

так что q=10.2600, а первый остаток от деления равен

95.5181у²+14.5141у³-103.2409у⁴+,

откуда р’=95.5181. Так как коэффициенты первого остатка не малы, то следует продолжать действие дальше.

Производится деление всех членов первого остатка на р’у²:

S’=1+0.1519у-1.0808у²-0.0761у³+

Результатом деления S на S’ является второе частное 1+у² -9.4119у, второй остаток равен нулю.

Таким образом, рассчитаны следующие значения величин p, q, p’, q’:

Для ряда S1		Для ряда S2
р==-1001.1864	p’=-1.1579	р=-77.1864	p’=95.5181
q=0.1597	q’=0.6884	q=10.2600	q’=-9.4119

Так как сигнал содержит две гармоники, то круговые частоты находятся по формулам

, ,

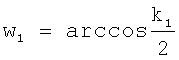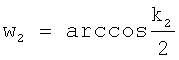где 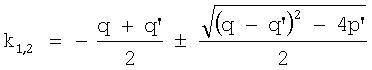. Параметры сигнала равны:

Для ряда S1		Для ряда S2
k1=0.6840	k2=-1.5321	k1=12.7643	k2=-13.6124
w1=1.2217	w2=2.4435

Для ряда S₁ рассчитанные круговые частоты совпадают с истинными значениями. Для ряда S₂ найти круговые частоты не представляется возможным, так как не выполняется условие -21,2<2. Полученные значения параметров попадают в область неопределенности, следовательно, найти значения амплитуд гармоник невозможно. Получить модель сигнала не представляется возможным.

Совокупность действий для получения модели сигнала с помощью предлагаемого способа.

С выхода ДАС поступают измерения анализируемого сигнала (t=1). В блоке 1 рассчитывается на основе (6) идентифицирующая матрица:

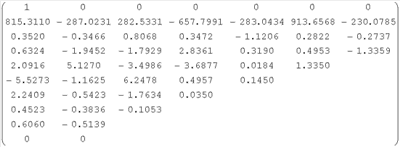
На вход блока 2 подается ДПФ:

.

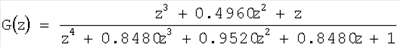Значения параметров ДПФ обрабатываются в блоке 2 и определяются круговые частоты w₁=2.4435, w₂=1.2217 и амплитуды A₁=593, А₂=462. На выходе блока 2 снимают прогнозирующую модель сигнала

х^м(kt)=593sin(2.4435kt)+462sin(1.2217kt),

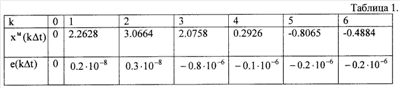
содержащую две скрытых периодичности, и подают ее на вход блока 3. Результаты расчетов модельных значений сигнала в блоке 3 приведены в Табл.4, где х^м(kt) -модельные значения сигнала, рассчитанные с помощью предлагаемого способа, e(kt)=x(kt)-х^м(kt) – погрешности модельных значений. Сравнение экспериментальных и модельных значений сигнала электрического тока позволяет сделать заключение о точном (с точностью до вычислительных погрешностей) модельном его восстановлении.

Формула изобретения

Способ анализа многочастотных сигналов, содержащих скрытые периодичности с использованием непрерывных цепных дробей путем измерения сигнала в равноотстоящие промежутки времени, отличающийся тем, что сигнал подают с датчика анализируемых сигналов в идентификатор непрерывной цепной С-дроби, в котором последовательно проводят обработку значений сигнала по формуле:

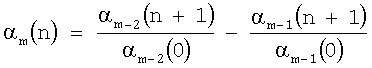
до выполнения правила останова, где _-1(n)=(n) – дельта функция Дирака, ₀(n)=х(n) – измерения сигнала, m=1,2,3,, n=0,1,2,, с последующим восстановлением прогнозирующей модели сигнала в форме скрытой периодичности.

РИСУНКИ