Патент на изобретение №2397077

(54) СПОСОБ ОПРЕДЕЛЕНИЯ УЗЛОВОГО ВЗАИМНОГО СОПРОТИВЛЕНИЯ В ТЯГОВОЙ СЕТИ ЖЕЛЕЗНЫХ ДОРОГ

(57) Реферат:

Изобретение относится к системе тягового электроснабжения электрических железных дорог переменного тока. Способ заключается в том, что включают установку поперечной емкостной компенсации (КУ) на шины в первом узле, измеряют ее ток 1К, изменение напряжения на шинах U₁, изменение вектора тока между первым и вторым узлами Iу относительно напряжения в первом узле, рассчитывают комплексное сопротивление тяговой сети Zmc и определяют узловое взаимное сопротивление между первым и вторым узлами в тяговой сети по выражению: Z₂₁=(U₁+ZmcIу)/Iк. Технический результат заключается в повышении точности определения узлового взаимного сопротивления между узлами. 1 ил.

Изобретение относится к системе тягового электроснабжения электрических железных дорог переменного тока, а именно к расчетам и оптимизации режима системы тягового электроснабжения.

Сложные электрические сети рассчитывают матричными методами с использованием, в частности, узловых собственных и взаимных сопротивлений сети. Из [1] известно «узловое сопротивление представляет собой комплексный коэффициент пропорциональности между напряжением в узле и одним из задающих токов при отсутствии в схеме других задающих токов и равенстве нулю всех эдс».

Например, для двухузловой схемы узловое взаимное сопротивление равно

где U₂ – напряжение в узле 2 при задающем токе I₁ в узле 1.

Узловые матрицы сопротивлений используются в расчетах и оптимизации режима систем тягового электроснабжения [2, 3].

Определение узлового сопротивления из [1, стр.236 – прототип] позволяет найти узловое взаимное сопротивление следующим способом: включить нагрузку в узле 2, замерить напряжение в узле 1 и выполнить расчет по выражению (1).

Недостатки этого способа

1. Не всегда возможно отключить и включить нагрузку для измерений.

2. Рассматриваемые узлы могут находиться друг от друга на большом расстоянии, в сотни и более километрах, поэтому может быть затруднительна синхронизация измерений.

3. При малых значениях Z₂₁ точность измерений резко падает.

Процесс определения узлового сопротивления более эффективен при наличии установки поперечной емкостной компенсации (КУ) в узлах тяговой сети железных дорог [4]. КУ использовалась раньше при определении узлового собственного сопротивления [5], однако здесь рассматривается определение узлового взаимного сопротивления.

Цель изобретения – повышение точности определения взаимного сопротивления для условий тяговых сетей переменного тока.

Поставленная цель достигается тем, что согласно способу определения узлового взаимного сопротивления в тяговой сети железных дорог с установкой поперечной емкостной компенсации, основанному на измерении тока и напряжения в узлах тяговой сети, включают установку поперечной емкостной компенсации (КУ) на шины в первом узле, измеряют ее ток Iк, изменение напряжения на шинах U₁ 1-го узла, изменение вектора тока между первым и вторым узлами Iy относительно напряжения в первом узле, рассчитывают комплексное сопротивление тяговой сети Zmc и определяют узловое взаимное сопротивление между первым и вторым узлами в тяговой сети по выражению:

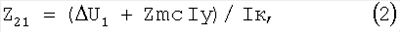
Таким образом, предлагаемый способ позволяет следующее.

1. Вместо операций с включением-отключением нагрузки выполнять переключения установки поперечной емкостной компенсации, что достаточно просто и безболезненно в условиях эксплуатации.

2. Расчет выполнить с использованием данных измерений изменения токов и напряжений при включении КУ.

3. Все измерения производить на одной подстанции (в 1-ом узле).

4. Измерения напряжения в удаленном 2-м узле заменить измерением тока между узлами и последующим расчетом, что повышает точность определения Z₂₁.

Все указанное приводит к повышению точности расчета.

И еще очень важное преимущество рассмотренного способа определения Z₂₁.

В существующих нормативных документах по расчету системы тягового электроснабжения(СТЭ) система внешнего электроснабжения (СВЭ) в лучшем случае представлена узловыми собственными сопротивлениями, которые передаются от энергоснабжающих организаций в максимальном и минимальном режимах питающих сетей 110(220) кВ. В реальных режимах узловые сопротивления отличаются от указанных, о чем свидетельствуют измерения, проведенные на тяговых подстанциях Горьковской ж.д.

Поэтому рассматриваемый способ, во-первых, определяет реальные значения узловых сопротивлений при совместном рассмотрении систем СВЭ и СТЭ, и во-вторых, определяет узловые взаимные сопротивления.

По-существу, предлагаемый способ является основой оценивания и идентификации режима системы тягового электроснабжения [6]. С его помощью система тягового электроснабжения совместно с СВЭ заменяется математической моделью с квадратной матрицей узловых сопротивлений.

На чертеже представлена схема системы тягового электроснабжения 25 кВ, поясняющая предлагаемый способ.

Система внешнего электроснабжения представлена двумя источниками питания E₁ и Е₂, сопротивлениями линий Z₁, Z₂, Z₃. Тяговая сеть с сопротивлением Zmc подключена между двумя узлами 1 и 2, которые подключены соответственно к тяговым трансформаторам с сопротивлениями Zm₁ и Zm₂. В узле 1 включена КУ.

Алгоритм определения Z₂₁

1. При отключенной КУ измеряем напряжение U_1(o) и Iy(о).

2. Включаем КУ, измеряем Iк.

3. При включенной КУ повторно измеряем U_1(в) и I_у(в).

4. Рассчитываем U₁=U_1(в)-U_1(o) и

Iy=I_у(в)-I_y(о).

5. Рассчитываем Z₂₁ по выражению (2).

Так как при включении КУ практически изменяется продольная составляющая напряжения U_1(o), то геометрическую разность (U_1(в)-U_1(o)) можно заменить на арифметическую и считать, что вектора U₁ и U_1(в) находятся в фазе. Вектор Iy ориентируем относительно U_1(в).

Покажем, что указанная формула (2) расчета Z₁₂ повышает точность определения узлового взаимного сопротивления.

В (1) заменим I₁ на Iк, a U₂ выразим

U₂=U₁+Zmc Iy,

где U₁ – изменение напряжения в первом узле,

Iy – изменение вектора тока между узлами 1 и 2, измерения проводятся в 1-м узле,

Z_mc – комплексное сопротивление тяговой сети между 1-м и 2 м узлами.

С учетом указанного получим выражение (2).

При малых Z₁₂ изменение напряжения во 2-м узле будет малым. С учетом погрешности приборов погрешность разности измеренных напряжений, то-есть изменения напряжений (при отключенном и затем включенном КУ), может быть недопустимой (например, расчет изменения измеренных напряжений с 27 кВ до 27,2 кВ, то есть 0,2 кВ, может дать погрешность 50% и более).

В то же время точность определения изменения тока Iу значительно выше. Что касается сопротивления тяговой сети, то в настоящее время существуют выверенные способы его определения [7].

Так как нагрузочные узлы в тяговой сети постоянно перемещаются вслед за токоприемником электроподвижного состава (ЭПС), то формула (2) позволяет после проведенной по вышеуказанному алгоритму процедуры измерений U₁, I и Iк (достаточно провести измерения один раз) определять аналитически взаимные сопротивления между 1-м узлом и любым узлом тяговой сети между узлами 1 и 2. Для этого необходимо задавать значение Zmc для требуемого узла в тяговой сети.

Обычно число нагрузочных узлов в тяговой сети ограничивают числом перегонов.

При Zmc=0 определяется узловое собственное сопротивление узла 1.

Примеры расчета режима тяговых сетей с использованием матриц узловых сопротивлений приведены в [8].

Используемые источники

1. Веников В.А., Глазунов А.А., Жуков Л.А., Солдаткина Л.А. Электрические системы, т.2. Электрические сети. Под ред. В.А.Веникова. М.: Высш. школа, 1971. 440 с.

2. Герман Л.А Матричные методы расчета системы тягового электроснабжения. Конспект лекций, ч.1. М.: РГОТУПС, 1998, 36 с.

3. Герман Л.А. Матричные методы расчета системы тягового электроснабжения. Конспект лекций. ч.2. М.: РГОТУПС, 2000, 42 с.

4. Бородулин Б.М., Герман Л.А., Николаев Г.А. Конденсаторные установки электрифицированных железных дорог. М.: Транспорт, 1983, 136 с.

5. Заявка на изобретение 2008111317 «Способ регулирования напряжения тяговой подстанции переменного тока (авторы Герман Л.А. и др.)». Положительное решение от 22.01.2009 г.

6. Гусейнов Ф.Г., Рахманов Н.Р. Оценка параметров и характеристик энергосистем. М.: Энергоатомиздат, 1988, 153 с.

7. Фигурнов Е.П. Релейная защита. М.: Желдориздат., 2002. 720 с.

8. Герман Л.А., Горшкова Л.А. Матричные методы расчета системы тягового электроснабжения (расчет типовых задач). Учебное пособие. М.: РГОТУПС, 2004, 28 с.

Формула изобретения

Способ определения узлового взаимного сопротивления в тяговой сети железных дорог с установкой поперечной емкостной компенсации, основанный на измерении тока и напряжения рассматриваемых двух узлов, отличающийся тем, что включают установку поперечной емкостной компенсации (КУ) на шины в первом узле, измеряют ее ток Iк, изменение напряжения на шинах U₁, изменение вектора тока между первым и вторым узлами I_у относительно напряжения в первом узле, рассчитывают комплексное сопротивления тяговой сети Zmc и определяют узловое взаимное сопротивление между первым и вторым узлами в тяговой сети по выражению:
Z₂₁=(U₁+Zmc I_у)/Iк

РИСУНКИ