|
|
(21), (22) Заявка: 2008134627/28, 27.08.2008
(24) Дата начала отсчета срока действия патента:
27.08.2008
(43) Дата публикации заявки: 10.03.2010
(46) Опубликовано: 27.06.2010
(56) Список документов, цитированных в отчете о
поиске:
RU 2301986 C1, 05.10.2005. Автореферат на соискание ученой степени кандидата химических наук (М.Н.Маланин «Спектроскопическое изучение пористости полимеров»). Тверь, 2007. RU 2321840 С1, 03.07.2006. US 2005228594 A1, 13.10.2005.
Адрес для переписки:
170044, г.Тверь, ул. Вагжанова, 14, АОЗТ ЦПТУ “Эффект”
|
(72) Автор(ы):
Маланин Михаил Николаевич (RU),
Пахомов Павел Михайлович (RU),
Хижняк Светлана Дмитриевна (RU)
(73) Патентообладатель(и):
Государственное образовательное учреждение Высшего профессионального образования Тверской государственный университет (RU)
|
(54) СПОСОБ ОПРЕДЕЛЕНИЯ СРЕДНЕГО РАЗМЕРА АГРЕГАТОВ ЧАСТИЦ НАПОЛНИТЕЛЯ, ИХ КОНЦЕНТРАЦИИ И РАСПРЕДЕЛЕНИЯ В ОБЪЕМЕ ПОЛИМЕРНОЙ МАТРИЦЫ
(57) Реферат:
Изобретение позволяет определить средний размер агрегатов частиц наполнителя, их концентрации и распределения в объеме полимерной матрицы. Заявленный способ заключается в изготовлении эталонных образцов, записи ИК-спектров пропускания эталонных образцов, идентификации экстремумов спектрограмм эталонных образцов в соответствии со средним размером частиц наполнителя, их концентрацией и распределением, построении градуировочных графиков. Далее производят запись ИК-спектров исследуемых образцов и соотнесении экстремумов спектрограмм исследуемых образцов с градуировочным графиком. Заявленное изобретение направлено на обеспечение определения средних размеров агрегатов частиц наполнителя, их концентрации и распределения в объеме полимерной матрицы. 2 табл., 9 ил.
Изобретение относится к области исследования частиц с помощью ИК-спектроскопии, а именно к области определения размера частиц и коэффициента пропускания.
Технический результат настоящего изобретения заключается в том, что ИК-спектроскопическим способом определяются средние размеры агрегатов частиц наполнителя, их концентрации и распределения в объеме полимерной матрицы.
Технический результат достигается тем, что изготавливаются эталонные образцы, записываются ИК-спектры пропускания эталонных образцов, идентифицируются экстремумы спектрограмм эталонных образцов в соответствии со средним размером агрегатов частиц наполнителя, их концентрацией и распределением, установленными с помощью электронного микроскопа, построении градуировочных графиков, записи ИК-спектров исследуемых образцов и соотнесении экстремумов исследуемых образцов с градуировочным графиком.
Изобретение поясняется таблицами и графическими материалами.
Таблица 1. Соотношение коэффициентов преломления в системе полимерная матрица/наполнитель.
Таблица 2. Соотношение коэффициентов преломления в полимерных смесях (полимерная матрица/полимер-наполнитель).
Фиг.1. Схема взаимодействия электромагнитного излучения с веществом. Заштрихованные области – частицы наполнителя, расположенные в полимерной матрице (незаштрихованная область).
Фиг.2. Схематическое строение наполненного (смесевого) материала.
Фиг.3. ПК-спектры полимерных композитов (а – полистирол-ТЮ, 6 – ПС-тальк, в – ПП-СаСО, г – ПП-монтмориллонит) в зависимости от степени наполнения: а – 0(1), 1(2), 5(3), 10(4), 20(5) и 30% (6); б-г – 0(1), 10(2), 20(3) и 30% (4); нумерация спектров идет сверху вниз.
Фиг.4. Электронно-микроскопические снимки композитов с разными наполнителями: а – ПС-30% TiO, 6 – ПС-30% тальк, в – ПП -30% СаСО, г – ПП-30% монтмориллонит.
Фиг.5. ИК-спектры пропускания полимерных смесей на основе ПС (а, б) и ПММА (в, г) с облученным (а, в) и термомеханически обработанным (б, г) ПТФЭ, используемым в качестве наполнителя, в зависимости от степени наполнения: 1-0; 2-10; 3-20; 4-30 и 5-40% (нумерация спектров идет сверху вниз).
Фиг.6. Распределение частиц наполнителя по размерам, рассчитанное из данных Фиг.5, для полимерных смесей ПС-ПТФЭ (а, б) и ПММА-ПТФЭ (в, г) в зависимости от степени наполнения: 1-10; 2-20; 3-30 и 4-40% (а, в – облученный ПТФЭ; в, г – термомеханически обработанный ПТФЭ).
Фиг.7. Зависимость среднего размера частиц ПТФЭ, определенного из данных Фиг.6, от его концентрации в смесях с ПС (1, 2) и ПММА (3, 4); 1 и 3 – облученный, а 2 и 4 – термомеханически обработанный ПТФЭ.
Фиг.8. Электронно-микроскопические снимки полимерных смесей на основе ПММА-30% ПТФЭ для облученного (а) и термомеханически обработанного ПТФЭ (б).
Фиг.9. Распределение частиц ПТФЭ по размерам в полимерных смесях с ПС: термомеханически обработанный (а), облученный ПТФЭ (б).
1 – данные электронной сканирующей микроскопии;
2 – данные ИК-спектроскопии.
Сущность изобретения заключается в следующем. Для придания полимерному материалу необходимых свойств (механических, термических, электрических, адгезионных и др.) в него вводят частицы органических и неорганических наполнителей, а также других полимеров. При этом важно, чтобы наполнитель равномерно распределялся по объему полимерной матрицы и не агрегировался в частицы больших размеров. Путем смешения, например, гибко- и жесткоцепных полимеров можно плавно и существенно изменять те или иные свойства материала. К настоящему времени имеется большое разнообразие способов приготовления полимерных смесей и композитов: их получают через расплав или раствор, путем направленного синтеза, смешением на микро- или макроуровнях. Однако для эффективного и направленного создания смесей и композитов с заданными свойствами необходимо знать размеры агрегатов, которые часто образуются из частиц наполнителя, их распределение по размерам и концентрацию. Если на поверхности наполненного материала эти агрегаты можно анализировать с помощью методов электронной и оптической микроскопии, то в объеме образца такой анализ затруднен.
Заявляемый способ позволяет определять концентрации и размеры агрегатов частиц наполнителя (микронный диапазон), а также их распределение по размерам с использованием ИК-спектроскопии. При прохождении ИК-излучения через «мутную» среду (например, пористый или наполненный полимерный образец толщиной l) (Фиг.1) происходит ослабление его интенсивности за счет поглощения и рассеяния на границах с наполнителем. При этом интенсивность падающего излучения I0 уменьшается до величины прошедшего излучения IT. Коэффициент затухания (или ослабления) излучения е включает в себя поглощательную  A и рассеивающую A и рассеивающую  S части. Математически это можно выразить следующим образом: S части. Математически это можно выразить следующим образом:

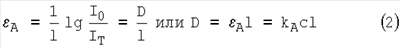
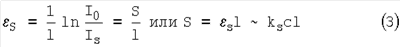
где D – оптическая плотность, S – величина рассеяния излучения, kA и kS – коэффициенты поглощения и рассеяния соответственно, с – концентрация поглощающих или рассеивающих центров, I0 – интенсивность падающего света, IS и IT – соответственно интенсивности рассеянного и прошедшего через образец излучения.
Следует отметить, что формулы (1-3) справедливы, если показатель поглощения <<1. Кроме того, важно, что kS зависит от размера и формы частиц.
Таким образом, коэффициенты ослабления за счет поглощения и рассеивания пропорциональны концентрации поглощающих CA и рассеивающих частиц CS, а также коэффициентам поглощения kA и рассеяния kS соответственно. Общая толщина наполненной полимерной пленки l или длина пути, которую проходит свет в образце, состоит из суммы длин путей, проходимых в материале полимера lм и наполнителя: lнl=lм+lн (Фиг.2).
Сравнивая ИК-спектры наполненных и ненаполненных пленок, всегда легко определить степень наполнения полимера. Таким образом, выделение и анализ поглощательной и рассеивающей компонент ИК-излучения могут дать информацию об общем содержании вещества матрицы или наполнителя в полимерной смеси (или композите).
В том случае, когда размеры (d) рассеивающих частиц (поры или частицы наполнителя) совпадают с длиной волны (А,) падающего излучения, происходит существенное снижение светопропускания, в результате в ИК-спектре наблюдается характерный «минимум». Определение среднего размера рассеивающих частиц и их распределения по размерам основано на принципе резонанса: коэффициент рассеяния в случае дифракционного рассеяния (d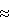  ) существенно больше, чем для случая рэлеевского рассеяния ( ) существенно больше, чем для случая рэлеевского рассеяния ( >>d, малые рассеивающие частицы) или рассеяния Ми ( >>d, малые рассеивающие частицы) или рассеяния Ми ( < <
Следует также отметить, что для хорошего проявления эффекта рассеяния в ИК-спектре образца необходимо выполнение следующих условий
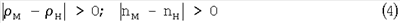
где  м, nм и м, nм и  н, nн – соответственно плотность и показатель преломления вещества матрицы или наполнителя. Именно на условии |nм-nн| н, nн – соответственно плотность и показатель преломления вещества матрицы или наполнителя. Именно на условии |nм-nн|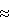 0 основан принцип действия иммерсионной жидкости для снижения эффекта рассеяния при записи ИК-спектра образца. 0 основан принцип действия иммерсионной жидкости для снижения эффекта рассеяния при записи ИК-спектра образца.
Были исследованы два типа образцов: полимерные композиты с наполнителями различной природы (табл.1) и полимерные смеси (табл.2). Композиции составляли таким образом, чтобы в изучаемых системах варьировалась разница коэффициентов преломления матрицы и наполнителя. Композиты получали через расплав (температура расплава указана в табл.1) в двухшнековом экструдере «DSM 15» при скорости вращения 100 об/мин, время перемешивания составляло 5 мин. В табл.1 представлены характеристики материала и наполнителя. Четыре типа полимерных смесей готовили на двухшнековом экструдере «Haake-Laborkneter» при скорости вращения 100 об/мин и температуре 220°С. Исходный гранулят полимерной матрицы подвергали плавлению в течение 3 мин, затем добавляли второй полимерный компонент и смесь выдерживали при температуре плавления матрицы еще в течение 5 мин.
Для записи ИК-спектров из полученных композитных заготовок готовили пленки путем прессования под давлением 3 т/см2 при нагреве. Толщина пленок составляла от 15 до 35 мкм. ИК-спектры пленок записывали на Фурье-ПК спектрометре «Equinox 55», фирмы «Bruker» в диапазоне 7000-400 см-1 и на Фурье-ИК микроскопе «Hyperion 1000» в диапазоне 4000-600 см-1.
Распределение частиц в объеме контролировали с помощью сканирующего электронного микроскопа «Leo VP435» фирмы «Carl Zeiss», для чего после выдерживания в жидком азоте получали сколы с полимерных заготовок (экструдатов). Состояние наполнителя на поверхности пленки изучали на оптическом микроскопе «Axiotech» («Carl Zeiss») в поляризованном свете. Анализ микроскопических снимков с целью получения распределения частиц в объеме полимерного материала и на поверхности пленки осуществляли с помощью программы «Image Pro».
При анализе ИК-спектров композитов отмечается уменьшение пропускания с ростом концентрации наполнителя по сравнению с пропусканием исходной полимерной матрицы – не одинаково для различных композиций полимер-наполнитель (Фиг.3). Наибольшее снижение пропускания обнаружено в случае наполнения полимерной матрицы двуокисью титана (на Фиг.3а представлен композит с двуокисью титана на основе ПС). Для полимерных композитов с двуокисью титана лучше всего выполняется условие (4) – разница между коэффициентами преломления максимальна (табл.1). Установлено также, что во всех композитах с тальком практически не наблюдается снижения пропускания (Фиг.3б). Однако в системах с карбонатом кальция, имеющим одинаковый с тальком коэффициент преломления (1,57), снижение пропускания происходит (Фиг.3в), но в меньшей степени, чем в композитах с TiO2. Что касается монтмориллонита, то оказалось, что эффект снижения пропускания проявляется слабее, чем для карбоната кальция (Фиг.3г) (еще меньший коэффициент преломления – 1,51), и зависит в большей степени от типа полимерной матрицы.
На электронно-микроскопических снимках полимерных композитов, представленных на Фиг.4, хорошо видно, что форма и размер частиц различных наполнителей сильно отличаются. Особым образом выглядит структура композита на основе талька. Из-за плоской слоисто-чешуйчатой структуры частицы талька имеют большие размеры, и рассеяние в ИК-спектрах композитов на его основе не наблюдается, так как для его проявления нужно, чтобы размер частиц был близок к длине волны. Исходные частицы монтмориллонита, по сравнению с другими наполнителями, обладают наименьшими (нанометровыми) размерами, и в микронном (ИК) диапазоне они начинают «проявляться», то есть приводят к снижению светопропускания, только при больших степенях наполнения из-за агрегации частиц.
Способ осуществляется следующим образом.
Вначале изготавливаются эталонные образцы. Затем определяются средние размеры агрегатов частиц наполнителя, их концентрации и распределение с помощью электронного микроскопа. Записываются ИК-спектры пропускания эталонных образцов и идентифицируются экстремумы спектрограмм в соответствии со средним размером агрегатов частиц наполнителя, их концентрацией и распределением. Далее записываются ИК-спектры исследуемых образцов, а экстремумы спектрограмм соотносятся с градуировочными графиками эталонных образцов.
Примеры выполнения способа.
ИК-спектры полимерных смесей представлены на Фиг.5. Для пар ПС-ПТФЭ и ПММА-ПТФЭ эффект снижения пропускания выражен очень четко, и мы можем видеть разницу в форме «минимума» спектра для области 7000-2000 см-1. Именно этот «минимум» содержит информацию о среднем размере частиц наполнителя, их распределении по размерам и агрегации. На Фиг.6 показаны распределения частиц по размерам, рассчитанные из ИК-спектров. Из данных (Фиг.6) следует, что модифицированному (облученному) ПТФЭ соответствует меньший средний размер частиц и более узкое распределение по размерам в двух полимерных матрицах. Именно уменьшение размера частиц и, как следствие, рост их общей удельной поверхности в совокупности с активацией поверхности частиц ПТФЭ при облучении вызывает улучшение их адгезии к материалу матрицы.
На Фиг.7 представлены зависимости средних размеров частиц наполнителя от их концентрации, полученные из спектральных данных Фиг.6. Во всех случаях с ростом степени наполнения средний размер рассеивающих частиц, которому соответствует максимум на кривых распределения частиц по размерам, увеличивается. Данный факт свидетельствует об агрегации исходных частиц в агломераты и росте их среднего размера с увеличением степени наполнения. Если сравнивать две полимерные матрицы – ПС и ПММА, то оказывается, что частицы наполнителя как облученного, так и термомеханически обработанного, имеют меньший размер в ПММА матрице. Вследствие этого частицы ПТФЭ могут иметь лучшую адгезию к ПММА матрице.
Результаты обработки ИК-спектров подтверждаются микроскопическими снимками (Фиг.8). Разница в размере частиц ПТФЭ (облученного и термомеханически обработанного) в ПС матрице наглядно выражена. Облучение частиц ПТФЭ ведет к снижению их размеров и лучшей адгезии к ПС. В результате из частиц ПТФЭ образуются агрегаты меньших размеров, поскольку этим частицам становится “выгодней” агрегировать с частицами ПС, чем между собой, и полимерная смесь становится более гомогенной.
На Фиг.9 представлены данные по сопоставлению распределения частиц ПТФЭ в смеси с ПС, полученные с помощью методов электронной сканирующей микроскопии (кривая 1) и ПК-спектроскопии (кривая 2). Распределения частиц по размерам практически совпадают, что свидетельствует о достоверности использования предлагаемого способа.
Предлагаемый способ может быть использован в практике создания композитов с определенными свойствами для определения среднего размера частиц наполнителя, их распределения по размерам, агрегации – при условии, что размер частиц наполнителя попадает в микронный диапазон и существует разница между коэффициентами преломления и плотностью полимерной матрицы и наполнителя.
| Таблица 1 |
| Полимер матрицы |
Коэффициент преломления |
| Двуокись титана (TiO2) |
Тальк |
Карбонат кальция (СаСО3) |
Монтмориллонит |
| ПП |
1,49/2,7 |
1,49/1,57 |
1,49/1,57 |
1,49/1,51 |
| ПЭТФ |
1,57/2,7 |
1,57/1,57 |
1,57/1,57 |
1,57/1.51 |
| ПС |
1,59/2,7 |
1,59/1,57 |
1,59/1,57 |
1,59/1,51 |
| Таблица 2 |
| Полимерная матрица |
Коэффициент преломления |
| ПТФЭ |
ПТФЭ |
| ПС |
1.59/1.35 |
1.59/1.35 |
| ПММА |
1.49/1.35 |
1.49/1.35 |
Формула изобретения
Способ определения среднего размера агрегатов частиц наполнителя, их концентрации и распределения в объеме полимерной матрицы, заключающийся в изготовлении эталонных образцов, состоящих из полимерной матрицы и наполнителя, причем 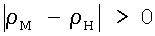 ; ; 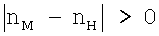 , где , где  м, nм и м, nм и  н, nн – соответственно плотность и показатель преломления вещества матрицы или наполнителя, записи ИК-спектров пропускания эталонных образцов, идентификации экстремумов спектрограмм эталонных образцов в соответствии со средним размером частиц наполнителя, их концентрацией и распределением, построении градуировочных графиков, записи ИК-спектров исследуемых образцов и соотнесении экстремумов спектрограмм исследуемых образцов с градуировочным графиком. н, nн – соответственно плотность и показатель преломления вещества матрицы или наполнителя, записи ИК-спектров пропускания эталонных образцов, идентификации экстремумов спектрограмм эталонных образцов в соответствии со средним размером частиц наполнителя, их концентрацией и распределением, построении градуировочных графиков, записи ИК-спектров исследуемых образцов и соотнесении экстремумов спектрограмм исследуемых образцов с градуировочным графиком.
РИСУНКИ
,> |
|