Патент на изобретение №2388076
|
||||||||||||||||||||||||||||||||
(54) СПОСОБ РАЗМЕЩЕНИЯ ОТСЧЕТОВ БЫСТРОГО ПРЕОБРАЗОВАНИЯ ФУРЬЕ В ПАМЯТИ ДАННЫХ
(57) Реферат:
Изобретение относится к вычислительной технике и может быть использовано при построении параллельных вычислительных систем. Техническим результатом является возможность одновременного доступа к отсчетам быстрого преобразования Фурье, размещенным в памяти традиционным способом. Указанный технический результат достигают тем, что в прямоугольной матрице отсчетов размерностью s×m, где: s – количество строк, m – количество столбцов, причем s*m равно 2p, m равно 2q, а р и q – целые числа и q больше или равно 1, а р больше q, для всех строк прямоугольной матрицы отсчеты, находящиеся в одной строке, размещают в столбцах с циклическим сдвигом относительно прямоугольного размещения вправо (влево) на Sh позиций:
Изобретение относится к вычислительной технике и может быть использовано при построении параллельных вычислительных систем. Известно устройство – синергическая вычислительная система (пат.
где RD – операция чтения, MOV ~j – передача результата выполнения команды предыдущего яруса j-того процессорного элемента на следующий ярус; MULC ~j, Wi – комплексное умножение результата выполнения команды предыдущего яруса j-того процессорного элемента на коэффициент; ADDC ~j, ~i, SUBC ~j, ~i – операции комплексного сложения и комплексного вычитания, соответственно, результатов j-того и i-того процессорных элементов с предыдущего яруса, WR – операция записи. Таким образом, для четырех отсчетов (а, b, с, d) две ступени вычисления «бабочек» выполняются за шесть шагов. Каждый процессорный элемент имеет в своем составе память данных, в которой размещаются введенные отсчеты для выполнения преобразования. Для m процессорных элементов, где m равно 2q, a q – целое число больше или равно 1, массив 2p отсчетов, где р – целое число больше q, можно представить в виде прямоугольной матрицы размерностью s×m. Введенные отсчеты могут быть записаны построчно:
либо по столбцам
Очевидно, что и в первом, и во втором случае наиболее быстро вычисляется только q ступеней преобразования. При построчном размещении – это первые ступени быстрого преобразования Фурье с прореживанием по времени. При размещении по столбцам – это также первые ступени, но с использованием быстрого преобразования Фурье с прореживанием по частоте. Для вычисления «бабочек» на последующих ступенях преобразования необходимо выбирать отсчеты, которые размещаются в памяти данных одного процессорного элемента. При этом меняется программа вычисления «бабочки» и каждый процессорный элемент начинает работать автономно. Это увеличивает количество команд на вычисление «бабочки» и, следовательно, снижает быстродействие синергической вычислительной системы, что является недостатком как первого, так и второго способа размещения отсчетов в памяти данных. Следует отметить, что этот недостаток присущ любой параллельной системе, использующей указанный способ размещения отсчетов. Задача настоящего изобретения – повышение производительности параллельных вычислительных систем при выполнении быстрого преобразования Фурье. Поставленная задача решается тем, что в указанной прямоугольной матрице отсчетов размерностью s×m, где s – количество строк, m – количество столбцов, причем s*m равно 2р, m равно 2q, а р и q – целые числа и q больше или равно 1, а р больше q, согласно изобретению для всех строк прямоугольной матрицы отсчеты, находящиеся в одной строке, размещают в столбцах с циклическим сдвигом относительно прямоугольного размещения вправо (влево) на Sh позиций:
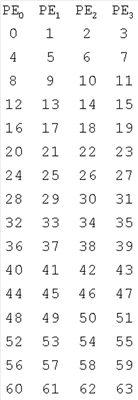
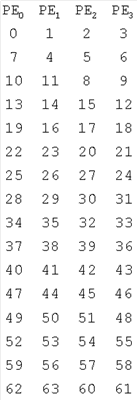
где n=[p-q+1]/q-1; si – коэффициент номера строки sn, представленной в виде sn=snmn+ Признаки в указанной взаимосвязи в процессе проведения поиска на новизну не обнаружены, являются существенными и в своей совокупности обеспечивают повышение производительности параллельных вычислительных систем при вычислении быстрого преобразования Фурье. Достигается это тем, что при предложенном «закрученном» размещении отсчетов в m блоках памяти данных с возможностью одновременной выборки, на любой ступени вычисления быстрого преобразования Фурье обеспечивается одновременная выборка всех необходимых на данном шаге отсчетов. Рассмотрим быстрое преобразование Фурье с прореживанием по времени на 64 отсчета(26), которые размещены в 4-х блоках памяти процессорных элементов. В исходном состоянии отсчеты (с учетом бит-реверсивной перестановки) введены и хранятся в памяти данных построчно (в соответствующих позициях матрицы приведены номера отсчетов):
Очевидно, что первые две ступени, содержащие «вырождение бабочки», не требуют перестановки отсчетов. Для выполнения первых двух «бабочек» третьей и четвертой ступеней необходимы отсчеты с номерами {0, 4, 8, 12}, которые находятся в памяти данных нулевого процессорного элемента. Разместим отсчеты в соответствии с предлагаемым способом, осуществляя циклический сдвиг вправо:
Необходимые отсчеты теперь размещаются в разных столбцах и могут быть прочитаны одновременно (одним ярусом команд). Так как отсчеты размещаются в разных строках, то для вычисления номера строки, в соответствующем блоке памяти, можно воспользоваться формулой: v=[sn/qcf]*qcf+(sn mod qcf+npe*(m**(cf-1)))mod qcf, где v – номер строки; sn – текущий номер строки (номер шага), изменяется от 0 до s-1; qcr=m*cf, если m**cf cf – номер прохода по массиву отсчетов, а именно вычисление первой и второй ступеней – «0-ой» проход, вычисление третьей и четвертой ступеней – 1-ый проход и т.д., количество ступеней, реализуемых за один проход по массиву отсчетов, определяется m; npe – номер процессорного элемента (номер блока памяти). Для выполнения последующих «бабочек» третьей и четвертой ступеней при sn=1 будет выбран набор отсчетов с номерами {7, 11, 15, 3}, при sn=2 – {10, 14, 2, 6}, при sn=3 – {13, 1, 5, 9}, при sn=4 – {19, 23, 27, 31} и т.д. Выбранный набор отсчетов должен быть переставлен местами путем циклического сдвига влево на m-Sh позиций, а массив коэффициентов должен быть сформирован в соответствии с порядком выборки отсчетов. В синергической вычислительной системе предложенный способ размещения может быть реализован следующим образом: (a) в состав процессорного элемента вводятся аппаратно модифицируемые регистры, содержащие sn, cf, а также регистры, содержащие значения m и s, задаваемые программистом; (b) вводится режим модификации адресов доступа к коммутатору, позволяющий динамически изменить заданное программистом значение на аппаратно формируемую константу; (c) вводятся две специализированные команды «чтение из массива отсчетов» и «запись в массив отсчетов». Команда «чтение из массива отсчетов» (мнемокод SRD) имеет один операнд М – адрес массива отсчетов и на основании значений sn, cf, m, s формирует исполнительный адрес для чтения отсчета, а также формирует значение константы модификации адреса доступа к коммутатору для команды следующего и только следующего яруса. Это значение равно величине обратного сдвига и суммируется с адресом коммутатора. Так для cf=1 и sn=1 величина константы будет равна 4-1=3 и команда MOV ~0 в последовательности команд: РЕ0 SRD M MOV ~0 передаст на следующий ярус значение, считанное РЕ3. Команда «запись в массив отсчетов» имеет два операнда – записываемое значение и адрес массива отсчетов. На основании значений sp, sf, m, s она формирует исполнительный адрес для записи отсчета, формирует значение обратного сдвига как константу для модификации своего адреса доступа к коммутатору и модифицирует его путем вычитания ее из адреса. Модифицирует значения sn, а после выполнения последнего шага очередного прохода – значение cf.
Формула изобретения
Способ построчного размещения или размещения по столбцам отсчетов быстрого преобразования Фурье в виде прямоугольной матрицы размерностью sxm, где s – количество строк, m – количество столбцов, причем s×m равно 2p, m равно 2q, а р и q – целые числа и q больше или равно 1, а р больше q, расположенной в памяти данных параллельной вычислительной системы, состоящей из m блоков данных с возможностью одновременной выборки, каждый из которых содержит отсчеты соответствующего столбца, отличающийся тем, что для всех строк прямоугольной матрицы все отсчеты, находящиеся в одной строке, размещают в столбцах с циклическим сдвигом относительно прямоугольного размещения вправо (влево) на Sh позиций:
|
||||||||||||||||||||||||||||||||
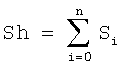, где n=[p-q+1]/q-1; si – коэффициент номера строки sn, представленной в виде sn=snmn+
+s2m2+s1m1+s0m0.
2179333 RU). Система состоит из N функциональных блоков, в качестве которых могут использоваться процессорные элементы, и полносвязного коммутатора. Архитектура процессорных элементов и коммутатора обеспечивают реализацию параллелизма на командном уровне, представленного в виде ярусно-параллельной формы. Так, например, фрагмент программы, обеспечивающий вычисление «бабочек» быстрого преобразования Фурье для системы, состоящей из четырех процессорных элементов, будет иметь следующий вид:
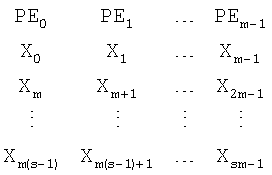
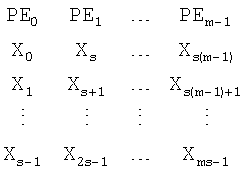
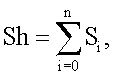
s, иначе qcf=s;