|
|
(21), (22) Заявка: 2008144676/09, 13.11.2008
(24) Дата начала отсчета срока действия патента:
13.11.2008
(46) Опубликовано: 27.04.2010
(56) Список документов, цитированных в отчете о
поиске:
RU 2234732 C1, 20.08.2004. GB 1173900 A, 10.12.1969. SU 1755299 A1, 15.08.1992. SU 1683042 A1, 07.10.1991.
Адрес для переписки:
143072, Московская обл., Одинцовский р-н, Кубинка-2, ул. Генерала Вотинцева, Московский военный институт радиоэлектроники Космических войск
|
(72) Автор(ы):
Горячкин Валерий Викторович (RU)
(73) Патентообладатель(и):
Министерство обороны Российской Федерации Государственное образовательное учреждение высшего профессионального образования Московский военный институт радиоэлектроники Космических войск (МВИРЭ КВ) (RU)
|
(54) УСТРОЙСТВО ВЫБОРА ОПТИМАЛЬНЫХ РЕШЕНИЙ МЕТОДОМ НАИМЕНЬШИХ РАССТОЯНИЙ
(57) Реферат:
Изобретение относится к области вычислительной техники и может быть использовано для выбора оптимальных решений из ряда возможных вариантов. Техническим результатом является расширение функциональных возможностей устройства, заключающееся в определении лучшего варианта на основе метода наименьших расстояний, для характеристики каждого из которых используется по k>2 частных показателей. Устройство содержит k>2 матриц N×M элементов памяти показателей, k>2 групп по N блоков выбора минимума, k>2 блоков выбора максимума, k>2 групп по N вычитателей, N блоков вычисления расстояний и N индикаторов. 1 ил.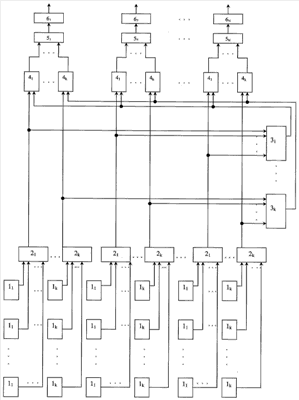
Изобретение относится к области специализированной вычислительной техники, а именно к устройствам для выбора оптимальных решений из ряда возможных вариантов как при проектировании, так и в процессе эксплуатации сложных систем.
Известно устройство для выбора оптимальных решений [1], содержащее в своем составе матрицу элементов памяти показателей, блоки выбора максимума, блоки выбора минимума, вычитатель, коммутирующие элементы, две группы умножителей, группу сумматоров, группу индикаторов и несколько шин задания исходных данных.
Работа устройства представляет собой процесс вычисления для каждого из рассматриваемых вариантов обобщенного показателя качества, выражаемого в виде суммы двух произведений. В качестве сомножителей используются максимальное и минимальное значения из совокупности всех частных показателей, характеризующих данный вариант, а также задаваемый показатель оптимизации либо дополнение его до единицы.
Недостатком известного устройства является ограниченность его функциональных возможностей, заключающаяся в том, что оно не обеспечивает выбора оптимального варианта на основе известного метода «наименьших расстояний» [2] по k>2 частных показателей.
Наиболее близким к заявляемому является «Устройство для выбора оптимальных решений методом наименьших расстояний» [3], выбранное в качестве прототипа и являющееся основным техническим решением.
Устройство для выбора оптимальных решений содержит элементы памяти показателей, образующие две матрицы размерностью N×M, где N – количество сопоставляемых вариантов, а М – количество составляющих каждый вариант объектов, характеризующихся значениями двух частных показателей, блоки выбора минимума, образующие две группы по N блоков в каждой, два блока выбора максимума, вычитатели, образующие две группы по N вычитателей в каждой, N блоков вычисления расстояний и N индикаторов.
Каждый блок выбора минимума имеет М входов и один выход. Их задачей является выбор из N величин, поступающих на его входы, наибольшей и выдача ее на выход.
Каждый вычитатель имеет по два входа и одному выходу. Назначением вычитателей является вычисление абсолютной величины разности сигналов, поступающих по его входам, и выдача полученной разницы на выход.
Каждый блок вычисления расстояний имеет по два входа и одному выходу. Их задачей является вычисление длины гипотенузы прямоугольного треугольника по длинам его катетов, представляемым в виде сигналов, поступающих по его двум входам.
Задачей индикаторов является индикация на табло значений длин отрезков, поступающих на их входы в виде соответствующих сигналов.
Составные части, образующие устройство, соединены между собой следующим образом:
входы ij-х 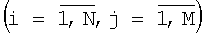 элементов памяти показателей первой матрицы соединены со входами соответствующих i-х элементов памяти показателей первой матрицы соединены со входами соответствующих i-х 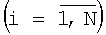 блоков выборов минимума первой группы, выходы которых соединены со входами первого блока выбора максимума; блоков выборов минимума первой группы, выходы которых соединены со входами первого блока выбора максимума;
выходы ij-х 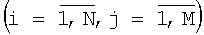 элементов памяти показателей второй матрицы соединены со входами соответствующих i-х элементов памяти показателей второй матрицы соединены со входами соответствующих i-х 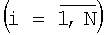 блоков выбора минимума второй группы, выходы которых соединены со входами второго блока выбора максимума; блоков выбора минимума второй группы, выходы которых соединены со входами второго блока выбора максимума;
выход каждого i-го 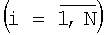 блока выбора минимума каждой группы соединен с первым входом соответствующего i-го блока выбора минимума каждой группы соединен с первым входом соответствующего i-го 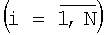 вычитателя соответствующей группы; вычитателя соответствующей группы;
выход первого блока выбора максимума соединен со вторыми входами всех N вычитателей первой группы;
выход второго блока выбора максимума соединен со вторыми входами всех N вычитателей второй группы;
выходы i-х 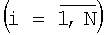 вычитателей первой и второй группы соединены со входами соответствующих i-х блоков вычисления расстояний, выходы которых соединены со входами соответствующих индикаторов. вычитателей первой и второй группы соединены со входами соответствующих i-х блоков вычисления расстояний, выходы которых соединены со входами соответствующих индикаторов.
Недостатком данного устройства является ограниченность функциональных возможностей, заключающаяся в том, что оно не обеспечивает выбор оптимального варианта на основе «метода наименьших расстояний», для характеристики каждого из которых используется по k частных показателей, где k>2.
Целью данного изобретения является расширение функциональных возможностей устройства для определения оптимальных решений, заключающихся в осуществлении определения лучшего варианта на основе метода наименьших расстояний, для характеристики каждого из которых используются по k частных показателей, где k>2.
Указанная цель достигается тем, что в устройство дополнительно вводятся k>2 матриц N×М элементов памяти показателей, k>2 групп по N блоков выбора минимума, k>2 блоков выбора максимума, k>2 групп по N вычитателей при соответствующей схеме соединения их между собой и остальными элементами устройства
Сравнительный анализ с прототипом показывает, что заявляемое устройство отличается наличием дополнительных элементов при соответствующем схемном решении. Таким образом, заявляемое устройство соответствует критерию изобретения «новизна».
Сравнение заявляемого устройства с другими аналогичными техническими решениями показывает, что благодаря дополнительному введению в состав устройства k>2 матриц N×M элементов памяти показателей, k>2 групп по N блоков выбора минимума, k>2 блоков выбора максимума и k>2 групп по N вычитателей при соответствующей схеме соединения их между собой и с остальными элементами устройства появляются новые свойства заявляемого устройства, проявляющиеся в расширении его функциональных возможностей, а именно в осуществлении определения лучшего варианта на основе метода наименьших расстояний, для характеристики каждого из которых используется по k частных показателей, где k>2. Это позволяет сделать вывод о соответствии заявляемого технического решения критерию «существенные отличия».
Сущность метода наименьших расстояний при выборе оптимальных решений для k>2 состоит в следующем.
Рассматриваются N возможных вариантов некоторой сложной системы, в каждом из которых содержится М объектов, каждый из которых описывается посредством значений k частных показателей, где k>2. Из N возможных вариантов требуется выбрать наилучший (оптимальный).
В каждом из N возможных вариантов рассматриваются все М объектов. Благодаря наличию k>2 частных показателей каждый из N составляемых вариантов можно изобразить в виде точки в k-мерном декартовом пространстве, где по каждой из к осей откладываются значения k-го частного показателя. В этом же k-мерном пространстве можно представить точку, координаты которой по каждой оси представляют собой максимальные значения соответствующих координат точек составляемых вариантов. Оптимальным вариантом признается тот, у которого расстояние в k-мерном декартовом пространстве (k>2) от его точки до точки с максимальным значением координат будет минимальным:
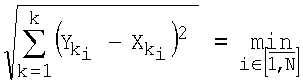 , ,
где 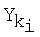 – максимальное значение k-го показателя для i-го варианта; – максимальное значение k-го показателя для i-го варианта;
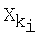 – значение k-го показателя, характеризующее i-й вариант; – значение k-го показателя, характеризующее i-й вариант;
k – общее количество показателей (k>2);
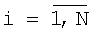 порядковый номер составляемого варианта; порядковый номер составляемого варианта;
N – общее количество составляемых вариантов.
На чертеже представлена функциональная схема предлагаемого устройства.
Устройство для выбора оптимальных решений содержит k>2 матриц N×M элементов памяти показателей 11, 12,  , 1k, k>2 групп по N блоков выбора минимума 21, 22, , 1k, k>2 групп по N блоков выбора минимума 21, 22,  , 2k, k>2 блоков выбора максимума 31, 32, , 2k, k>2 блоков выбора максимума 31, 32,  , 3k, k>2 групп по N вычитателей 41, 42, , 3k, k>2 групп по N вычитателей 41, 42,  , 4k, N блоков вычисления расстояний 51, 52, , 4k, N блоков вычисления расстояний 51, 52,  , 5N, и N индикаторов 61, 62, , 5N, и N индикаторов 61, 62,  , 6N, где k>2. , 6N, где k>2.
Таким образом, в состав предлагаемого устройства входят элементы памяти k>2 показателей, образующие k>2 матриц размерностью N×M, где N – количество составляемых вариантов, а М – количество составляющих каждый вариант объектов, характеризующихся значениями k>2 частных показателей, блоки выбора минимума, образующие k>2 групп по N блоков в каждой, k>2 блоков выбора максимума, вычитатели, образующие k>2 групп по N вычитателей в каждой, N блоков вычисления расстояний и N индикаторов.
Каждый k-й блок выбора минимума 21, 22,  , 2k имеет М входов и один выход. Их задачей является выбор из М величин, поступающих на его входы, наименьшей и выдача ее на выход. , 2k имеет М входов и один выход. Их задачей является выбор из М величин, поступающих на его входы, наименьшей и выдача ее на выход.
Каждый k-й блок выбора максимума 31, 32,  , 3k имеет N входов и один выход. Их задачей является выбор из N величин, поступающих на его входы наибольшей и выдача ее на выход. , 3k имеет N входов и один выход. Их задачей является выбор из N величин, поступающих на его входы наибольшей и выдача ее на выход.
Каждый k-й вычитатель 41, 42,  , 4k имеет по два входа и одному выходу. Назначением вычитателей является вычисление абсолютной величины разности сигналов, поступающих по его входам, и выдача полученной разницы на выход. , 4k имеет по два входа и одному выходу. Назначением вычитателей является вычисление абсолютной величины разности сигналов, поступающих по его входам, и выдача полученной разницы на выход.
Каждый i-й блок вычисления расстояний 5l, 52,  , 5N имеет по k>2 входов и одному выходу. Их задачей является вычисление расстояний в k-мерном декартовом пространстве (k>2) для каждого i-го варианта в соответствии с соотношением вида , 5N имеет по k>2 входов и одному выходу. Их задачей является вычисление расстояний в k-мерном декартовом пространстве (k>2) для каждого i-го варианта в соответствии с соотношением вида 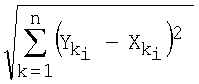 . .
Задачей индикаторов 61, 62,  , 6N является индикация на табло значений длин отрезков в k-мерном пространстве, поступающих на их входы в виде соответствующих сигналов. Выходы индикаторов являются выходом устройства. , 6N является индикация на табло значений длин отрезков в k-мерном пространстве, поступающих на их входы в виде соответствующих сигналов. Выходы индикаторов являются выходом устройства.
Составные части, образующие предлагаемое устройство, соединены между собой следующим образом:
выходы ij-х 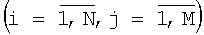 элементов памяти показателей 12, 12, элементов памяти показателей 12, 12,  , 1k k-й матрицы соединены со входами соответствующих i-х , 1k k-й матрицы соединены со входами соответствующих i-х 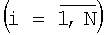 блоков выбора минимума 21, 22, блоков выбора минимума 21, 22,  , 2k k-й группы, выходы которых соединены со входами 31, 32, , 2k k-й группы, выходы которых соединены со входами 31, 32,  , 3k k-го блока выбора максимума и с первым входом i-го вычитателя 41, 42, , 3k k-го блока выбора максимума и с первым входом i-го вычитателя 41, 42,  , 4k k-й группы; , 4k k-й группы;
выходы 31, 32,  , 3k k-х блоков выбора максимума соединены со вторыми входами всех N вычитателей 41, 42, , 3k k-х блоков выбора максимума соединены со вторыми входами всех N вычитателей 41, 42,  , 4k k-х групп; , 4k k-х групп;
выходы i-х 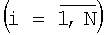 вычитателей 41, 42, вычитателей 41, 42,  , 4k k-х групп соединены со входами соответствующих i-х блоков вычисления расстояний 51, 52, , 4k k-х групп соединены со входами соответствующих i-х блоков вычисления расстояний 51, 52,  , 5N, выходы которых соединены со входами соответствующих i-х индикаторов 61, 62, , 5N, выходы которых соединены со входами соответствующих i-х индикаторов 61, 62,  , 6N, выходы которых являются выходом устройства. , 6N, выходы которых являются выходом устройства.
Устройство работает следующим образом. В процессе подготовки устройства к работе в каждый ij-й элемент памяти показателей k-й матрицы N×M записываются значения k-го показателя соответствующих j-х объектов i-го варианта.
В результате поступления с выходов элементов памяти k-х частных показателей объектов сопоставляемых вариантов на входы соответствующих групп блоков выбора минимума 21, 22,  , 2k, на выходах i-х , 2k, на выходах i-х 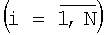 блоков выбора минимума 21, 22, блоков выбора минимума 21, 22,  , 2k k-й группы появятся сигналы, представляющие собой минимальные значения k-х частных показателей для совокупности из М соответствующих объектов N сопоставляемых вариантов. , 2k k-й группы появятся сигналы, представляющие собой минимальные значения k-х частных показателей для совокупности из М соответствующих объектов N сопоставляемых вариантов.
С выходов блоков выбора минимума 21, 22,  , 2k. k-й группы минимальные значения k-х частных показателей сопоставляемых вариантов поступают на первые входы соответствующих вычитателей 41, 42, , 2k. k-й группы минимальные значения k-х частных показателей сопоставляемых вариантов поступают на первые входы соответствующих вычитателей 41, 42,  , 4k k-й группы и на входы k-го блока выбора максимума 31, 32, , 4k k-й группы и на входы k-го блока выбора максимума 31, 32,  , 3k, с выхода которого максимальное значение из совокупности минимальных значений k-х частных показателей сопоставляемых вариантов поступает на вторые входы всех N вычитателей 41, 42, , 3k, с выхода которого максимальное значение из совокупности минимальных значений k-х частных показателей сопоставляемых вариантов поступает на вторые входы всех N вычитателей 41, 42,  , 4k k-й группы. , 4k k-й группы.
Значение разности между максимальными значениями из совокупности минимальных значений исследуемых вариантов и минимальными значениями соответствующих вариантов по всем k>2 частным показателям с выходов соответствующих k-х групп вычитателей 41, 42,  , 4k по k>2 поступают на входы соответствующих блоков вычисления расстояний 51, 52, , 4k по k>2 поступают на входы соответствующих блоков вычисления расстояний 51, 52,  , 5N, с выходов которых значения соответствующих расстояний каждого из сопоставляемых вариантов поступают на входы соответствующих индикаторов 61, 62, , 5N, с выходов которых значения соответствующих расстояний каждого из сопоставляемых вариантов поступают на входы соответствующих индикаторов 61, 62,  , 6N, где и высвечивается на табло. , 6N, где и высвечивается на табло.
Оператору остается только проанализировать высвеченные значения, принадлежащие сопоставляемым вариантам, и выбрать в качестве оптимального тот вариант, значение «расстояния» которого будет наименьшим.
Из приведенного описания работы заявляемого устройства видно, что в нем в отличие от прототипа осуществляется сопоставление сравниваемых вариантов с целью выявления лучшего на основе метода наименьших расстояний для характеристик каждого из которых используется по k частных показателей, где k>2.
Источники информации
1. Авторское свидетельство СССР  1640716, МКИ G06G 7/122, 1991. 1640716, МКИ G06G 7/122, 1991.
2. Бронштейн И.Н., Семендяев К.А. Справочник по математике. – М.: «Наука», 1986, 544 с.
3. Патент RU 2234732 С1, 20.08.2004 г., МПК7 G06G 7/122, G06F 7/24.
Формула изобретения
Устройство для выбора оптимальных решений методом наименьших расстояний, содержащее N блоков вычисления расстояний и N индикаторов, причем входы индикаторов подключены к выходам соответствующих i-х блоков вычисления расстояний, а их выходы являются выходом устройства, отличающееся тем, что в его состав дополнительно введены k>2 матриц N×M элементов памяти показателей, k>2 групп по N блоков выбора минимума, k>2 блоков выбора максимума, k>2 групп по N вычитателей, при этом выходы ij-й 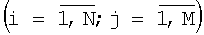 элементов памяти показателей k-й матрицы соединены со входами соответствующих i-х блоков выбора минимума k-й группы, выходы которых соединены со входами k-го блока выбора максимума и с первым входом i-го вычитателя k-й группы, выход k-го блока выбора максимума соединен со вторыми входами всех N вычитателей k-й группы, выходы i-х вычитателей всех k>2 групп соединены со входами соответствующих i-x блоков вычисления расстояний. элементов памяти показателей k-й матрицы соединены со входами соответствующих i-х блоков выбора минимума k-й группы, выходы которых соединены со входами k-го блока выбора максимума и с первым входом i-го вычитателя k-й группы, выход k-го блока выбора максимума соединен со вторыми входами всех N вычитателей k-й группы, выходы i-х вычитателей всех k>2 групп соединены со входами соответствующих i-x блоков вычисления расстояний.
РИСУНКИ
|
|