Патент на изобретение №2369973
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(54) СПОСОБ ФОРМИРОВАНИЯ И ПРОВЕРКИ ПОДЛИННОСТИ ЭЛЕКТРОННОЙ ЦИФРОВОЙ ПОДПИСИ, ЗАВЕРЯЮЩЕЙ ЭЛЕКТРОННЫЙ ДОКУМЕНТ
(57) Реферат:
Изобретение относится к области криптографических устройств. Техническим результатом настоящего изобретения является повышение производительности алгоритмов электронной цифровой подписи (ЭЦП) без снижения ее уровня стойкости. Сущность изобретения заключается в том, что способ генерации и проверки ЭЦП включает следующую последовательность действий: генерируют секретный ключ в виде многоразрядного двоичного числа (МДЧ) х, по секретному ключу формируют открытый ключ Y в виде матрицы МДЧ размерности w×w, где 2
Изобретение относится к области электросвязи и вычислительной техники, а конкретнее к области криптографических способов аутентификации электронных сообщений, передаваемых по телекоммуникационным сетям и сетям ЭВМ, и может быть использовано в системах передачи электронных сообщений (документов), заверенных электронной цифровой подписью (ЭЦП), представленной в виде многоразрядного двоичного числа (МДЧ). Здесь и далее под МДЧ понимается электромагнитный сигнал в двоичной цифровой форме, параметрами которого являются: число битов и порядок следования их единичных и нулевых значений1). ((1)толкование используемых в описании терминов приведено в Приложении 1). Известен способ формирования и проверки ЭЦП, предложенный в патенте США формируют секретный ключ в виде трех простых МДЧ p, q и d, формируют открытый ключ (n, e) в виде пары МДЧ n и e, где n – число, представляющее собой произведение двух простых МДЧ p и q, и е – МДЧ, удовлетворяющее условию ed=1 mod (p-1)(q-1), принимают электронный документ (ЭД), представленный МДЧ H; в зависимости от значения H и значения секретного ключа формируют ЭЦП в виде МДЧ Q=S=Hdmod n; формируют первое проверочное МДЧ A=H; формируют второе проверочное МДЧ B, для чего МДЧ S возводят в целочисленную степень e по модулю n: B=Se mod n; сравнивают сформированные проверочные МДЧ A и B; при совпадении параметров сравниваемых МДЧ A и B делают вывод о подлинности ЭЦП. Недостатком известного способа является относительно большой размер подписи и необходимость увеличения размера подписи при разработке новых более эффективных методов разложения числа n на множители или при росте производительности современных вычислительных устройств. Это объясняется тем, что значение элемента подписи S вычисляется путем выполнения арифметических операций по модулю n, а стойкость ЭЦП определяется сложностью разложения модуля n на множители p и q. Известен также способ формирования и проверки подлинности ЭЦП Эль-Гамаля, описанный в книге [Молдовян А.А., Молдовян Н.А., Советов Б.Я. Криптография. – СПб: Лань, 2000. – с.156-159], который включает следующие действия: формируют простое МДЧ p и двоичное число G, являющееся первообразным корнем по модулю p, генерируют секретный ключ в виде МДЧ x, в зависимости от секретного ключа формируют открытый ключ в виде МДЧ Y=Gxmod p, принимают ЭД, представленный в виде МДЧ H, в зависимости от H и секретного ключа формируют ЭЦП Q в виде двух МДЧ S и R, то есть Q=(S,R); осуществляют процедуру проверки подлинности ЭЦП, включающую вычисление двух контрольных параметров с использованием исходных МДЧ p, G, Y, H и S путем возведения МДЧ G, Y, R в дискретную степень по модулю p и сравнение вычисленных контрольных параметров; при совпадении значений контрольных параметров делают вывод о подлинности ЭЦП. Недостатком данного способа также является относительно большой размер ЭЦП. Это объясняется тем, что значения элементов подписи S и R вычисляют путем выполнения арифметических операций по модулю p – 1 и по модулю p, соответственно. Известен также способ формирования и проверки ЭЦП, предложенный в патенте США формируют простое МДЧ p, такое что p=Nq+1, где q – простое МДЧ; формируют простое МДЧ a, такое что a методом генерации случайной равновероятной последовательности формируют секретный ключ в виде МДЧ x; формируют открытый ключ в виде МДЧ принимают ЭД, представленный МДЧ М; формируют ЭЦП в виде пары МДЧ (е, s), для чего генерируют случайное МДЧ t, формируют МДЧ R по формуле R=at mod p, формируют МДЧ e=f(M||R), где знак || обозначает операцию присоединения двух МДЧ и f – некоторая специфицированная хэш-функция, значение которой имеет фиксированную длину (обычно 160 или 256 бит), независимо от размера аргумента, т.е. от размера МДЧ M||R, а затем формируют МДЧ s по формуле s=(t-ex) mod q; формируют первое проверочное МДЧ A, для чего генерируют МДЧ R’ по формуле R’=as формируют второе проверочное МДЧ B путем копирования МДЧ e: B=e; сравнивают сформированные проверочные МДЧ A и B; при совпадении параметров сравниваемых МДЧ A и B делают вывод о подлинности ЭЦП. Недостатком способа по патенту США является относительно высокая вычислительная сложность процедуры формирования и проверки ЭЦП, что связано с тем, что для обеспечения минимально требуемого уровня стойкости требуется использовать простой модуль p разрядностью не менее 1024 бит. Наиболее близким по своей технической сущности к заявленному является известный способ формирования и проверки подлинности ЭЦП, предлагаемый российским стандартом ГОСТ Р 34.10-2001 и описанный, например, в книге [Б.Я.Рябко, А.Н.Фионов. Криптографические методы защиты информации. М., Горячая линия – Телеком, 2005. – 229 с. (см. с.110-111)], согласно которому ЭЦП формируется в виде пары МДЧ r и s, для чего генерируют эллиптическую кривую (ЭК) в виде совокупности точек, причем каждая точка представляется двумя координатами в декартовой системе координат в виде двух МДЧ, называемых абсциссой (x) и ординатой (y), затем осуществляют операции генерации точек ЭК, сложения точек ЭК и умножения точки ЭК на число, а также арифметические операции над МДЧ, после чего в результате выполненных операций формируются МДЧ r и s. Указанные операции над точками выполняются как операции над МДЧ, являющимися координатами точек, по известным формулам [Б.Я.Рябко, А.Н.Фионов. Криптографические методы защиты информации. М., Горячая линия – Телеком, 2005. – 229 с. (см. с.110-111)]. Операция сложения двух точек А и В с координатами (xA, yA) и (xB, yB), соответственно, выполняется по формулам: xc=k2-xA-xB mod p и yc=k(xA-xc)-yA mod p, где nА=А+А+ Результатом умножения любой точки ЭК на нуль определяется точка, называемая бесконечно удаленной точкой и обозначаемой буквой О. Две точки A=(x, у) и -A=(x, -y) называются противоположными. Умножение на целое отрицательное число -n определяется следующим образом: (-n)A=n(-А). По определению принимают, что сумма двух противоположных точек равна бесконечно удаленной точке О. В прототипе, т.е. в способе формирования и проверки подлинности ЭЦП по стандарту ГОСТ Р 34.10-2001, генерируют ЭК, описываемую уравнением y2=x3+ax+b mod p, поэтому генерация ЭК состоит в генерации чисел a, b и p, являющихся параметрами ЭК и однозначно задающих множество точек ЭК, абсцисса и ордината каждой из которых удовлетворяет указанному уравнению. Ближайший аналог (прототип) заключается в выполнении следующей последовательности действий: генерируют эллиптическую кривую (ЭК), которая представляет собой совокупность пар МДЧ, называемых точками ЭК и над которыми задана операция сложения точек; методом генерации случайной равновероятной последовательности формируют секретные ключи в виде МДЧ k1, k2, формируют открытые ключи в виде точек ЭК P1, P2, принимают ЭД, представленный МДЧ H; генерируют случайное МДЧ 0 R=tG; формируют ЭЦП Q в виде пары МДЧ (r, s), для чего генерируют МДЧ r по формуле r=xR mod q, где xR – абсцисса точки R, а затем генерируют МДЧ s по формуле s=(tH+rki) mod q, где 1 формируют первое проверочное МДЧ A, для чего генерируют МДЧ v по формуле формируют второе проверочное МДЧ B путем копирования МДЧ r: B=r; сравнивают сформированные проверочные МДЧ A и B; при совпадении параметров сравниваемых МДЧ A и B делают вывод о подлинности ЭЦП. Недостатком ближайшего аналога является относительно невысокая производительность процедуры формирования и проверки ЭЦП, что связано с тем, что выполнение операций над точками ЭК включает операцию деления на МДЧ по модулю простого МДЧ, время выполнения которой в 10 и более раз превышает время выполнения операции умножения. Целью изобретения является разработка способа формирования и проверки подлинности ЭЦП, заверяющей ЭД, свободного от операции деления по модулю простого МДЧ, благодаря чему повышается производительность процедур формирования и проверки ЭЦП. Поставленная цель достигается тем, что в известном способе формирования и проверки подлинности ЭЦП, заверяющей ЭД, заключающемся в том, что генерируют секретный ключ в виде МДЧ x, по секретному ключу формируют открытый ключ Y в виде более чем одного МДЧ, принимают электронный документ, представленный МДЧ H, в зависимости от принятого электронного документа и от секретного ключа формируют электронную цифровую подпись Q в виде двух МДЧ, в зависимости от ЭД, ЭЦП и открытого ключа формируют первое A и второе B проверочные МДЧ, сравнивают их и при совпадении их параметров делают вывод о подлинности электронной цифровой подписи, согласно изобретению открытый ключ Y формируют в виде матрицы МДЧ размерности w×w, где 2 Новым является то, что открытый ключ Y формируют в виде матрицы МДЧ размерности w×w, где 2 Выполнение операции умножения матриц МДЧ включает выполнение над МДЧ операций сложения и умножения по модулю простого МДЧ. Благодаря тому что при выполнении операций умножения и возведения в степень матриц МДЧ не требуется выполнять операцию деления по модулю МДЧ, обеспечивается повышение производительности процедур формирования и проверки подлинности ЭЦП. Новым является также и то, что открытый ключ Y генерируют в виде матрицы МДЧ размерности 2×2, для чего генерируют матрицу МДЧ G размерности 2×2, имеющую порядок q, и открытый ключ Y формируют по формуле Y=Gx (mod p), а электронную цифровую подпись Q формируют в виде пары МДЧ e и s, для чего генерируют случайное МДЧ k, генерируют матрицу МДЧ R по формуле R=Gk (mod p), где p – МДЧ, являющееся модулем, по которому выполняются операции над МДЧ, входящими в состав матрицы МДЧ G при выполнении над G операции возведения в степень, затем формируют первое МДЧ e электронной цифровой подписи по формуле e=rH mod Новым является также и то, что генерируют матрицу МДЧ G размерности 2×2, значение определителя которой равно единице по модулю p. Новым является также и то, что открытый ключ Y генерируют в виде матрицы МДЧ размерности 3×3, для чего генерируют матрицу МДЧ G размерности 3×3, имеющую порядок q, и открытый ключ Y формируют по формуле Y=Gx (mod p), где p – МДЧ, являющееся модулем по которому выполняются операции над МДЧ, входящими в состав матрицы МДЧ G при выполнении над G операции возведения в степень, а электронную цифровую подпись Q формируют в виде пары МДЧ e и s, для чего генерируют случайное МДЧ k, генерируют матрицу МДЧ R по формуле R=Gk (mod p), затем формируют первое МДЧ е электронной цифровой подписи по формуле e=rH mod Новым является также и то, что генерируют матрицу МДЧ G размерности 3×3, значение определителя которой равно единице по модулю p. Конкатенацией двух чисел Матрица МДЧ – это набор МДЧ, расположенный в следующем виде.
Матрицу МДЧ обычно обозначают заглавной латинской буквой, например Q. Ее также записывают в сокращенном виде {qij}, i=1, 2,
либо по формуле
где p – простое МДЧ, cij – элемент матрицы С, являющейся результатом операции умножения матриц МДЧ Q и U. При вычислении по второй формуле и фиксированном размере МДЧ p матрицы МДЧ состоят из элементов конечного множества следующих МДЧ: 0, 1, 2, 3,
т.е. все диагональные элементы равны единице, а все остальные равны нулю. Выполнение операций над матрицами осуществляется в вычислительных устройствах как действия над двоичными цифровыми электромагнитными сигналами, осуществляемыми по определенным правилам, определяемым через операции над МДЧ. Определителем матрицы А размерности w×w, задаваемой набором чисел {aij}, называется алгебраическая сумма всевозможных произведений, включающих w сомножителей aij, взятых по одному из каждой строки и из каждого столбца таким образом, что в каждое произведение взят элемент из каждой строки и каждого столбца (ни в одно из произведений не входят два сомножителя, принадлежащие одной и той же строке или одному и тому же столбцу). При этом слагаемые, отвечающие четным перестановкам входят со знаком «плюс», а слагаемые, отвечающие нечетным перестановкам, – со знаком «минус» (детальное описание правил вычисления определителя можно найти в книге [А.И.Кострикин. Введение в алгебру. Основы алгебры. – М.: Физматлит. 1994. – 320 с.]). В заявленном способе используются матрицы, элементами которых являются МДЧ, принимающие значения от нуля до p-1 и над которыми выполняются операции сложения и умножения по модулю p. Для таких матриц значение определителя вычисляется по модулю p и находится в интервале от нуля до p-1, т.е. определитель равен некоторому значению d по модулю p, где 0 При соответствующем выборе размерности матриц и модуля p множество матриц МДЧ является конечным, и это конечное множество содержит подмножество матриц МДЧ, которое образует группу, причем порядок этой группы является достаточно большим. Группа – это алгебраическая структура (т.е. множество математических элементов, над которыми определена некоторая математическая операция), которая обладает заданным набором свойств: операция ассоциативна, результатом выполнения операции над двумя элементами является также элемент этой же структуры, существует нейтральный элемент такой, что при выполнении операции над ним и другим некоторым элементом a группы результатом является элемент g. Детальное описание теории групп дано в широко известной математической литературе, например в книгах [А.Г.Курош. Теория групп.- М.: изд-во «Наука», 1967. – 648 с.] и [М.И.Каргаполов, Ю.И.Мерзляков. Основы теории групп.- М.: изд-во «Наука. Физматлит», 1996. – 287 с.]. Операция, определенная над элементами группы, называется групповой операцией. Групповой операцией в конечной группе матриц является операция умножения матриц МДЧ, определенная через операции сложения и умножения элементов матрицы по модулю p. Группа называется циклической, если каждый ее элемент может быть представлен в виде g=an для некоторого натурального числа n, где a – элемент данной подгруппы, называющийся генератором или образующим элементом циклической подгруппы, и степень n означает, что над элементом a выполняются n последовательных операций, т.е. an=a Обычно при разработке способов формирования и проверки ЭЦП используются циклические группы большого простого порядка или группы, порядок которых делится нацело на большое простое число [Венбо Мао. Современная криптография. Теория и практика. – М., СПб, Киев. Издательский дом «Вильямc», 2005. – 763 с.]. При соответствующем задании группы матриц МДЧ это условие легко обеспечивается. При этом стойкость способов формирования и проверки ЭЦП определяется сложностью задачи дискретного логарифмирования, которая состоит в определении значения степени n, в которую надо возвести заданный элемент группы, чтобы результатом этой операции был некоторый другой заданный элемент группы [Молдовян Н.А. Практикум по криптосистемам с открытым ключом. – СПб. БХВ-Петербург, 2007. – 298 с.]. Поскольку групповая операция над матрицами МДЧ выполняется путем выполнения модульных умножений и сложений над МДЧ, являющимися элементами матриц МДЧ, достаточно высокая трудность задачи дискретного логарифмирования в группе матриц МДЧ достигается при сравнительно малом значении размера модуля p, благодаря чему обеспечивается сравнительно высокая производительность операции возведения матриц МДЧ в большую степень. Поскольку производительность процедур формирования и проверки ЭЦП определяется производительностью операции возведения в степень, то при использовании операций над матрицами МДЧ обеспечивается сравнительно высокая производительность процедур формирования и проверки ЭЦП. Порядком матрицы М называется наименьшее натуральное число q, такое что Mq=Е, т.е. такое, что результатом умножения матрицы М на саму себя q раз является единичная матрица Е. Корректность заявленного способа доказывается теоретически. Рассмотрим, например, варианты реализации заявленного способа по пп.3 и 4 формулы изобретения. Открытый ключ, соответствующий секретному ключу x, представляет собой матрицу МДЧ Y=Gx(mod p). Матрица МДЧ R генерируется по формуле R=Gk (mod p), а первое МДЧ в ЭЦП (e, s) вычисляется по формуле e=rH mod s=(k-ex) mod q, поэтому матрица МДЧ R’, генерируемая по формуле R’=YeGs (modp) и используемая для формирования первого проверочного МДЧ A, равна R’=YeGs(mod p)=GexGs(mod p)=Gex+(k-ex)(mod p)=Gk(mod p)=R. Поскольку матрицы МДЧ R’ и R одинаковы, то конкатенация МДЧ первой строки матрицы МДЧ R’ равна конкатенации МДЧ первой строки матрицы МДЧ R, т.е. r’=(r’11||r’12 ||r’13)=r=(r11||r12||r13), следовательно, A=r’H mod Рассмотрим примеры реализации заявленного технического решения с конкретными численными значениями использованных параметров. Использованные в примерах матрицы были сгенерированы с помощью программы, разработанной специально для генерации матриц, включая матрицы с заданным порядком, и выполнения операций над матрицами МДЧ. Приводимые в примере МДЧ записаны для краткости в виде десятичных чисел, которые в вычислительных устройствах представляются и преобразуются в двоичном виде, т.е. в виде последовательности сигналов высокого и низкого потенциала. Пример 1. Данный пример иллюстрирует вариант реализации заявленного способа по п.2 формулы изобретения (этот пример и остальные приводимые ниже примеры одновременно иллюстрируют и п.1 формулы изобретения). В данном примере формирование и проверка ЭЦП включает следующую последовательность действий. 1. Формируют простое число р, такое что p-1 содержит большой простой множитель q, т.е. p=Nq+1, где N – четное число: p=10005473, где q=2767 и N=3616. 2. Генерируют секретный ключ x в виде случайного МДЧ: x=33827005351925439685. 3. Формируют открытый ключ Y в виде матрицы размерности 5×5, для чего выполняют следующую последовательность действий: 3.1 Генерируют матрицу G размерности 5×5, значение определителя которой равно 1 по модулю p=10005473:
Полученная вспомогательная матрица МДЧ G имеет порядок q, т.е. для нее выполняется условие Gq mod p=Е, где Е – единичная матрица. 3.2 Генерируют матрицу Y по формуле Y=Gx (mod p):
Полученная матрица такова, что значение ее определителя по модулю p равно единице. Это имеет место в силу следующего известного математического факта: определитель произведения матриц равен произведению определителей матриц, являющихся сомножителями [А.Г.Курош. Курс высшей алгебры. – М.: «Наука», 1971. – 431 с.]. 4. Принимают ЭД, представленный, например, следующим МДЧ H (в качестве которого может быть взята, в частности, хэш-функция от ЭД): H=453463. 5. Формируют ЭЦП Q в виде пары чисел (e, s), для чего выполняют следующие действия: 5.1. Генерируют случайное число k: k=14793055334187273340. 5.2. Формируют матрицу R по формуле R=Gk (mod p):
5.3. Генерируют первый элемент e электронной подписи в виде МДЧ, вычисляемого по формуле e=rH mod 5.4. Формируют значение s путем выполнения операции, задаваемого формулой s=(k+ex)mod q: s=385. 6. Формируют первое проверочное МДЧ A, для чего выполняются следующие действия. 6.2. Генерируют матрицу R’=YeGs (mod p):
6.3. Генерируют МДЧ A по формуле A=r’H mod 7. Формируют второе проверочное МДЧ B путем копирования МДЧ е: B=e=36603270. 8. Сравнивают первое A и B второе проверочные МДЧ. Сравнение показывает, что параметры МДЧ A и B совпадают. Совпадение значений A и B означает, что ЭЦП является подлинной, т.е. относится к принятому ЭД, представленному МДЧ Н. Пример 2. Реализация заявленного способа по п.4 формулы изобретения (этот пример иллюстрирует частный вариант реализации п.3 формулы изобретения, отличающийся тем, что генерируется матрица G со значением определителя равным единице по модулю p). Предположим, что пользователю необходимо подписать сообщение, представленное МДЧ H. Для этого выполняется следующая последовательность действий. 1. Формируют простое число p, такое что p-1 содержит большой простой множитель q, т.е. p=Nq+1, где N – четное число: p=1213101055353860365198942393055406360449930466509, где q=910683421037711696704229; N=1332077676314286889695452. 2. Генерируют секретный ключ в виде случайного МДЧ x: x=26412233452258564873. 3. Формируют открытый ключ в виде матрицы Y размерности 2×2, значение определителя которой равно единице по модулю p, для чего выполняют следующую последовательность действий: 3.1 Генерируют матрицу G размерности 2×2, значение определителя которой по модулю p равно 1, причем такую, что ее порядок равен значению q: G=(1202355537700013630255474902061928748859377385024; 661780860731578736974963326904080423309318448732; 726266908513412605605689590295630046107457372564). Ввиду достаточно большой длины МДЧ, являющихся элементами матрицы G, каждый элемент матрицы указан отдельно, при этом строки матрицы разделены двойной наклонной чертой. В такой записи элементы матрицы g11, g12 g21 и g22 записаны последовательно сверху вниз в отдельных строках. 3.2 Генерируют матрицу Y по формуле Y=Gx (mod p): Y=(765668645922971131462637659176175002121265271912; 686546034364915360874564606107543524491696599648; 173718371623103935352742823316230007430864301765). 4. Принимают ЭД, представленный, например, следующим МДЧ H: H=435346457676523423. 5. Формируют ЭЦП Q в виде пары чисел (e, s), для чего выполняют следующие действия: 5.1. Пользователь генерирует случайное число k: k=27049461528626923206. 5.2. Затем формируют матрицу R путем выполнения операции, задаваемой формулой R=Gk (mod p): R=(455363329583359023625266899777316926640501013681; 193145359861504811918206048283567465987970607659; 385854600850718001481881779520448776959506610386). 5.3. Генерируют первый элемент e электронной цифровой подписи в виде МДЧ, вычисляемого по формуле e=rH mod
e=247157248. 5.4. Формируют второй элемент подписи s путем выполнения операции, задаваемой формулой s=(k-ex)mod q: s=714538875050403859391403. 6. Формируют первое проверочное МДЧ A, для чего выполняются следующие действия. 6.1. Генерируют матрицу R’=YeGs (mod p): Ye=(1054289836977813241220692865884055278112848775391; 412720594141934652505374888529868609136342061615; 497953129779437524509848233343978685201212761147) Gs=(557140970524604453256865016479207346842314027711; 654964802199660308072055093173837833684333897401; 246994405741321957387664288252066868517103968796) R’=(455363329583359023625266899777316926640501013681; 193145359861504811918206048283567465987970607659; 385854600850718001481881779520448776959506610386). 6.3. Генерируют МДЧ A по формуле A=r’H mod A=247157248. 7. Формируют второе проверочное МДЧ B путем копирования МДЧ е: B=e=247157248. 8. Сравнивают первое A и B второе проверочные МДЧ. Сравнение показывает, что параметры МДЧ A и B совпадают. Совпадение значений A и B означает, что сформированная ЭЦП является подлинной, т.е. относится к принятому ЭД, представленному МДЧ H. Пример 3. Реализация заявленного способа по п.6 формулы изобретения (частный вариант реализации п.5 формулы изобретения). 1. Формируют простое число p, такое что p-1 содержит большой простой множитель q, т.е. p=Nq+1, где N – четное число: p=882693152152073761004890298352885499372774448173, где q=985479877918161283757537; N=895698808195631774845356. 2. Генерирует секретный ключ x в виде случайного МДЧ: x=3451073958338264285. 3. Формируют открытый ключ Y в виде матрицы размерности 3×3, значение определителя которой по модулю p равно 1, для чего выполняют следующую последовательность действий: 3.1 Генерируют матрицу G размерности 3×3, значение определителя которой по модулю p равно 1, причем такую, что ее порядок равен значению q: G=(363721035304855322270717595705381196622143562753; 342045577522215337424809683133061190595364260060; 388524193794655360623939908830582907417739970436; 435124243767703655645468663573798796968229028088; 728967772850853898600948656958266412109957471628; 430092459273736209053619942186148755067683099452; 436091184234493207523503292485824458657311822562). Полученная дополнительная матрица G имеет порядок q, т.е. для нее выполняется условие Gq mod p=1. 3.2 Генерируют матрицу Y пo формуле Y=Gx (modp): Y=(793649427315761259406026831506906225041194804340; 645841333769727307401444994977369021466398790655; 805215282344370055909657251366622501259863265035; 554880153034978377878010779839396184509620640898; 353096382126238920667662144589525065608865066344; 138815970154523201194960482573446216625756028413; 653804408722869157056518320036150833843832588519). 4. Принимают ЭД, представленный, например, следующим МДЧ H (в качестве которого может быть взята, в частности, хэш-функция от ЭД): H=6756345234523465. 5. Формируют ЭЦП Q в виде пары чисел (e, s), для чего выполняют следующие действия: 5.1. Пользователь генерирует случайное число k: k=12860134276868188623. 5.2. Формируют матрицу R путем выполнения операции, задаваемых формулой R=Gk(mod p): R=(456138598778574934094067405707408823929620188965; 134838090968284020883275585101955145958537373351; 725194419963133604462301246966629245403495216092; 196023528841210323468350988094893160456639667948; 747287101147541789531616146212253869003469601318; 188409773319432556126047166877690183782372779200; 32009504965824735724901667917940853117887655802). 5.3. Генерируют первый элемент e электронной подписи в виде МДЧ, вычисляемого по формуле e=rH mod ( e=644117540. 5.5. Формируют значение s путем выполнения операции, задаваемого формулой s=(k+ex)mod q: s=640156557585861119001588. 6. Формируют первое проверочное МДЧ A, для чего выполняются следующие действия. 6.2. Генерируют матрицу R’=Yq-eGs(mod p)=Yq-eGs(mod p): q-e=985479877918160639639997; Yq-e=(480039256397844235392097964436954752722231271379; 43525703614678367797622053909289662734508446485; 594427188164364341885587693597522368397543407967; 795365846233004098177105822781927741349303132756; 543716309036298412258991999827654617223985145669; 180471582091367944622121423646832322388139112345; 140159879304206682557015533315183354508497921826) Gs=(630064404804120002899043649410178012882848244991; 275025358523863904761511873188319990669954654707; 192845503297590775248455116562714514304860114920; 404238445746336652176571611625346772176575052622; 496371813589504230909314363323196807492773807177; 836287570593455187972972244740643582757106958732; 881783771774713241919479482510519794701877329632) R’=(456138598778574934094067405707408823929620188965; 134838090968284020883275585101955145958537373351; 725194419963133604462301246966629245403495216092; 196023528841210323468350988094893160456639667948; 747287101147541789531616146212253869003469601318; 188409773319432556126047166877690183782372779200; 32009504965824735724901667917940853117887655802). 6.3. Генерируют МДЧ A по формуле A=r’Hmod МДЧ
A=644117540. 7. Формируют второе проверочное МДЧ B путем копирования МДЧ е: B=е=644117540. 8. Сравнивают первое A и B второе проверочные МДЧ. Сравнение показывает, что параметры МДЧ A и B совпадают. Совпадение значений A и B означает, что ЭЦП является подлинной, т.е. относится к принятому ЭД, представленному МДЧ H. Примеры 1-3 экспериментально подтверждают корректность реализации заявленного способа, что дополняет приведенное выше математическое доказательство корректности конкретных реализаций заявленного способа формирования и проверки ЭЦП, заверяющей ЭД. По аналогии с приведенными выше частными вариантами реализации заявленного способа можно построить другие частные варианты реализации с использованием матриц размерности 16×16 или 32×32. При использовании матриц МДЧ, имеющих сравнительно большую размерность, высокая криптографическая стойкость ЭЦП обеспечивается при меньшей размерности МДЧ, являющихся элементами матриц МДЧ. Например, при размерности 8×8, 16×16 или 32×32 разрядность указанных МДЧ может составлять 32, 16 или 8 бит, соответственно, что позволяет повысить быстродействие процедур формирования и проверки подписи при программной реализации для выполнения программ, реализующих заявляемый способ, на 32-разрядных, 16-разрядных или 8-разрядных микропроцессорах, соответственно. Приведенные выше примеры экспериментально подтверждают корректность реализации заявляемого способа, что дополняет приведенные выше математические доказательства корректности описанных конкретных реализаций заявленного способа формирования и проверки ЭЦП, заверяющей ЭД. Таким образом, показано, что заявляемый способ может быть положен в основу стойких систем ЭЦП, в которых процедуры формирования и проверки подписи являются свободными от операции деления на МДЧ по модулю МДМ, благодаря чему обеспечивается повышение производительности процедур формирования и проверки ЭЦП. Заявленный способ может быть положен в основу стойких систем ЭЦП, обеспечивающих повышение производительности устройств и программ формирования и проверки ЭЦП. Приведенные примеры и математическое обоснование показывают, что предлагаемый способ формирования и проверки подлинности ЭЦП работает корректно, технически реализуем и позволяет достичь сформулированного технического результата. Приложение 1 Толкование терминов, используемых в описании заявки 1. Двоичный цифровой электромагнитный сигнал – последовательность битов в виде нулей и единиц. 2. Параметры двоичного цифрового электромагнитного сигнала: разрядность и порядок следования единичных и нулевых битов. 3. Разрядность двоичного цифрового электромагнитного сигнала – общее число его единичных и нулевых битов, например число 10011 является 5-разрядным. 4. Электронная цифровая подпись (ЭЦП) – двоичный цифровой электромагнитный сигнал, параметры которого зависят от подписанного электронного документа и от секретного ключа. Проверка подлинности ЭЦП осуществляют с помощью открытого ключа, который зависит от секретного ключа. 5. Электронный документ (ЭД) – двоичный цифровой электромагнитный сигнал, параметры которого зависят от исходного документа и способа его преобразования к электронному виду. 6. Секретный ключ – двоичный цифровой электромагнитный сигнал, используемый для формирования подписи к заданному электронному документу. Секретный ключ представляется, например, в двоичном виде как последовательность цифр «0» и «1». 7. Открытый ключ – двоичный цифровой электромагнитный сигнал, параметры которого зависят от секретного ключа и который предназначен для проверки подлинности цифровой электронной подписи. 8. Хэш-функция от электронного документа – двоичный цифровой электромагнитный сигнал, параметры которого зависят от электронного документа и выбранного метода ее вычисления. 9. Многоразрядное двоичное число (МДЧ) – двоичный цифровой электромагнитный сигнал, интерпретируемый как двоичное число и представляемый в виде последовательности цифр «0» и «1». 10. Операция возведения числа S в дискретную степень A по модулю n – это операция, выполняемая над конечным множеством натуральных чисел {0, 1, 2, 11. Группа – это алгебраическая структура (т.е. множество математических элементов различной природы), над элементами которой задана некоторая операция и они обладают заданным набором свойств: операция ассоциативна, результатом выполнения операции над двумя элементами является также элемент этой же структуры, существует нейтральный элемент такой, что при выполнении операции над ним и другим некоторым элементом a группы результатом является элемент a. Детальное описание групп дано в книгах [А.Г.Курош. Теория групп. – М.: изд-во «Наукам, 1967. – 648 с.] и [М.И.Каргаполов, Ю.И.Мерзляков. Основы теории групп. – М.: изд-во «Наука. Физматлит», 1996. – 287 с.]. Операция, определенная над элементами группы, называется групповой операцией. 12. Циклическая группа – это группа, каждый элемент которой может быть представлен в виде g=an для некоторого натурального значения n, где a – элемент данной группы, называемый генератором или образующим элементом циклической группы. Степень n означает, что над элементом a выполняются n последовательных операций, т.е. выполняются вычисления по формуле an=a 13. Матрица многоразрядных двоичных чисел – это набор МДЧ, расположенный в следующем виде m строк и h столбцов. Матрицу также записывают в сокращенном виде {aij}, где i=1, 2, 14. Размерность матрицы – это два натуральных числа, означающие количество строк (w) и количество столбцов (h) в матрице. Размерность матрицы записывается в виде w×h. 15. Квадратной матрицей называется матрица, содержащая одинаковое число строк и столбцов и имеющая размерность w×w. 16. Над квадратными матрицами МДЧ определены операции сложения и умножения матриц МДЧ. Операции, определенные над матрицами, выполняются путем выполнения операций над элементами матриц, которыми являются некоторые МДЧ. В результате вычисляется набор новых МДЧ, которые являются элементами новой матрицы, являющейся результатом операции. Матрицы A и B называются равными, если выполняется равенство aij=bij для всех значений индексов. Детальное описание свойств матриц и действий над ними можно найти в широко доступных книгах: [А.И.Кострикин. Введение в алгебру. Основы алгебры. – М.: Физматлит. 1994. – 320 с.]. 17. Определителем матрицы А, задаваемой набором чисел {aij}, называется алгебраическая сумма всевозможных произведений коэффициентов aij, взятых по одному из каждой строки и из каждого столбца, причем слагаемые, отвечающие четным перестановкам, входят со знаком «плюс», а слагаемые, отвечающие нечетным перестановкам, – со знаком «минус» (детальное описание правил вычисления определителя можно найти в книге [А.И.Кострикин. Введение в алгебру. Основы алгебры. – М.: Физматлит. 1994. – 320 с.]). 18. Операция умножения квадратной матрицы А на квадратную матрицу В, представленых наборами чисел {aij} и {bij}, i=1, 2, 19. Операция возведения матрицы А в натуральную степень и определяется как n-кратное умножение матрицы А на саму себя: An=A·A·A· 20. Выполнение операций над матрицами осуществляется в вычислительных устройствах как действия над двоичными цифровыми электромагнитными сигналами, осуществляемыми по определенными правилам, определяемым через описание операций над МДЧ. 21. Порядком матрицы A циклической подгруппы называется наименьшее натуральное число q, такое что Aq=Е, т.е. такое, что результатом умножения матрицы А на саму себя q раз является единичная матрица Е. 22. Единичной матрицей Е – называется такая матрица {
т.е. все диагональные элементы равны единице, а все остальные равны нулю.
Формула изобретения
1. Способ генерации и проверки подлинности электронной цифровой подписи, заверяющей электронный документ, заключающийся в том, что генерируют секретный ключ в виде многоразрядного двоичного числа х, по секретному ключу формируют открытый ключ Y в виде более чем одного многоразрядного двоичного числа, принимают электронный документ, представленный многоразрядным двоичным числом Н, в зависимости от принятого электронного документа и от значения секретного ключа формируют электронную цифровую подпись Q в виде двух многоразрядных двоичных чисел, в зависимости от электронного документа, электронной цифровой подписи и открытого ключа формируют первое А и второе В проверочные многоразрядные двоичные числа, сравнивают их и при совпадении их параметров делают вывод о подлинности электронной цифровой подписи, отличающийся тем, что открытый ключ Y формируют в виде матрицы многоразрядных двоичных чисел размерности w×w, где 2 2. Способ по п.1, отличающийся тем, что открытый ключ Y генерируют в виде матрицы многоразрядных двоичных чисел размерности 2×2, где 2 3. Способ по п.1, отличающийся тем, что открытый ключ Y генерируют в виде матрицы многоразрядных двоичных чисел размерности 2×2, для чего генерируют матрицу многоразрядных двоичных чисел G размерности 2×2, имеющую порядок q, и открытый ключ Y формируют по формуле Y=Gx (mod р), где р – простое МДЧ, а электронную цифровую подпись Q формируют в виде пары многоразрядных двоичных чисел е и s, для чего генерируют случайное многоразрядное двоичное число k, генерируют матрицу многоразрядных двоичных чисел R по формуле 4. Способ по п.3, отличающийся тем, что генерируют матрицу многоразрядных двоичных чисел G размерности 2×2, значение определителя которой равно единице по модулю р. 5. Способ по п.1, отличающийся тем, что открытый ключ Y генерируют в виде матрицы многоразрядных двоичных чисел размерности 3×3, для чего генерируют матрицу многоразрядных двоичных чисел G размерности 3×3, имеющую порядок q, и открытый ключ Y формируют по формуле Y=Gx (mod р), где р – простое МДЧ, а электронную цифровую подпись Q формируют в виде пары многоразрядных двоичных чисел е и s, для чего генерируют случайное многоразрядное двоичное число k, генерируют матрицу многоразрядных двоичных чисел R по формуле R=Gk (mod р), затем формируют первое многоразрядное двоичное число е электронной цифровой подписи по формуле e=rH mod 6. Способ по п.5, отличающийся тем, что генерируют матрицу многоразрядных двоичных чисел G размерности 3×3, значение определителя которой равно единице по модулю р.
HE4A – Изменение адреса для переписки с обладателем патента Российской Федерации на изобретение
Новый адрес для переписки с патентообладателем:
Извещение опубликовано: 10.11.2009 БИ: 31/2009
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 w
w 4405829 от 20.09.1983 и детально описанный также и в книгах [1. М.А.Иванов. Криптография. М., КУДИЦ-ОБРАЗ, 2001; 2. А.Г.Ростовцев, Е.Б.Маховенко. Введение в криптографию с открытым ключом. С-Петербург, Мир и семья, 2001. – с.43]. Известный способ заключается в следующей последовательности действий:
4405829 от 20.09.1983 и детально описанный также и в книгах [1. М.А.Иванов. Криптография. М., КУДИЦ-ОБРАЗ, 2001; 2. А.Г.Ростовцев, Е.Б.Маховенко. Введение в криптографию с открытым ключом. С-Петербург, Мир и семья, 2001. – с.43]. Известный способ заключается в следующей последовательности действий: 1 и aq mod p=1;
1 и aq mod p=1; по формуле y=ax mod p;
по формуле y=ax mod p;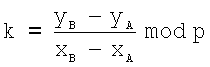 , если точки А и В не равны, и
, если точки А и В не равны, и 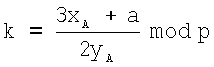 , если точки А и В равны. Операция умножения точки А на натуральное число n определяется как многократное сложение токи А:
, если точки А и В равны. Операция умножения точки А на натуральное число n определяется как многократное сложение токи А: +А (n раз).
+А (n раз). =sH-1 mod q и МДЧ w по формуле w=(q-rH-1) mod q, затем генерируют точку R’ по формуле R’=vG+wPi, после чего МДЧ A получают по формуле A=xR’ mod q, где: xR’ – абсцисса точки R’;
=sH-1 mod q и МДЧ w по формуле w=(q-rH-1) mod q, затем генерируют точку R’ по формуле R’=vG+wPi, после чего МДЧ A получают по формуле A=xR’ mod q, где: xR’ – абсцисса точки R’; , где r=(r11||r12) – МДЧ, равное конкатенации МДЧ первой строки матрицы МДЧ R, и
, где r=(r11||r12) – МДЧ, равное конкатенации МДЧ первой строки матрицы МДЧ R, и  и b, представленных в некоторой позиционной системе исчисления в виде a=a1a2a3
и b, представленных в некоторой позиционной системе исчисления в виде a=a1a2a3 Знак || обозначает операцию конкатенации.
Знак || обозначает операцию конкатенации.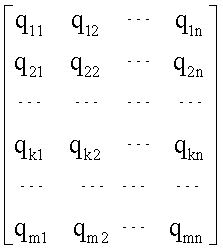
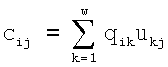
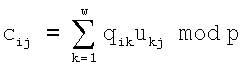
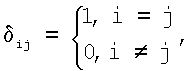
 a
a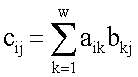 либо по формуле
либо по формуле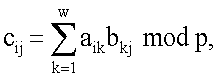 где p – простое МДЧ, сij – элемент матрицы С, являющейся результатом операции. При вычислении по второй формуле и фиксированном размере МДЧ p матрицы МДЧ состоят из элементов конечного множества следующих МДЧ: 0, 1, 2, 3,
где p – простое МДЧ, сij – элемент матрицы С, являющейся результатом операции. При вычислении по второй формуле и фиксированном размере МДЧ p матрицы МДЧ состоят из элементов конечного множества следующих МДЧ: 0, 1, 2, 3,