|
(21), (22) Заявка: 2007141832/09, 12.11.2007
(24) Дата начала отсчета срока действия патента:
12.11.2007
(46) Опубликовано: 20.06.2009
(56) Список документов, цитированных в отчете о
поиске:
SU 783811 А1, 30.11.1980. RU 2092899 С1, 10.10.1997. RU 2242791 С2, 20.12.2004. RU 2136041 С1, 27.08.1999. SU 1280385 А1, 30.12.1986. JP 3014173 A, 22.01.1991. US 6574650 B1, 03.06.2003.
Адрес для переписки:
634050, г.Томск, пр. Ленина, 30, Томский политехнический университет, отдел интеллектуальной и промышленной собственности
|
(72) Автор(ы):
Хамухин Александр Анатольевич (RU),
Бабушкин Юрий Владимирович (RU)
(73) Патентообладатель(и):
Государственное образовательное учреждение высшего профессионального образования Томский политехнический университет (RU)
|
(54) ЯЧЕЙКА ОДНОРОДНОЙ СТРУКТУРЫ ДЛЯ РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ
(57) Реферат:
Изобретение относится к области цифровой вычислительной техники и может быть использовано при построении различных специализированных устройств. Техническим результатом является расширение функциональных возможностей устройства для решения дифференциальных уравнений, содержащих частные производные не только по пространственным координатам, но и по времени. Ячейка содержит блок масштабных интеграторов, сумматор приращений, следящий интегратор, интегратор, ключевой элемент и блок формирования приращений от искомой переменной с предыдущих шагов по времени. 1 ил.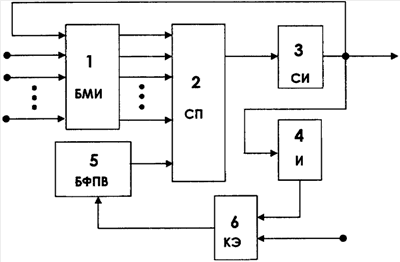
Изобретение относится к области цифровой вычислительной техники и предназначено для разработки и конструирования специализированных устройств для решения дифференциальных уравнений, содержащих частные производные по пространственным и временной координатам, а также для решения систем линейных алгебраических уравнений.
Известен процессор матричной вычислительной структуры для решения дифференциальных уравнений в частных производных, содержащий решающие блоки, регистры, блок памяти команд, блок памяти данных, блок микропрограммного управления и блоки оповещения (Авторское свидетельство СССР  1280385, МПК 3 G06F 15/32, опубл. 30.12.1986, бюл. 1280385, МПК 3 G06F 15/32, опубл. 30.12.1986, бюл.  48). Это устройство отличается универсальностью при реализации различных типов итерационных процедур вычислений, но его недостатком является избыточность и сложность реализации небольших задач. 48). Это устройство отличается универсальностью при реализации различных типов итерационных процедур вычислений, но его недостатком является избыточность и сложность реализации небольших задач.
Наиболее близким по технической сущности (прототип) к предлагаемому является ячейка однородной структуры для решения дифференциальных уравнений в частных производных, содержащая первый интегратор, блок масштабных интеграторов, выходы которого соединены со входами сумматора приращений, второй интегратор, выход которого соединен со входом первого интегратора и с одним из входов блока масштабных интеграторов, а вход второго интегратора подключен к выходу сумматора приращений (Авторское свидетельство СССР  783811, МПК 3 G06G 7/56, опубл. 30.11.1980, бюл. 783811, МПК 3 G06G 7/56, опубл. 30.11.1980, бюл.  44). 44).
Недостатком этой ячейки является невозможность прямого решения дифференциальных уравнений, содержащих частные производные не только по пространственным координатам, но и по времени.
Задачей изобретения является расширение функциональных возможностей ячейки однородной структуры для решения дифференциальных уравнений в частных производных.
Поставленная задача достигается тем, что в ячейку однородной структуры для решения дифференциальных уравнений в частных производных, содержащую так же, как в прототипе, интегратор, блок масштабных интеграторов, выходы которого соединены с входами сумматора приращений, следящий интегратор, выход которого соединен со входом интегратора и с одним из входов блока масштабных интеграторов, а вход следящего интегратора подключен к выходу сумматора приращений. Выходом ячейки для соединения с входами других ячеек однородной структуры является выход следящего интегратора, а входами ячейки для соединения с выходами других ячеек – входы блока масштабных интеграторов.
Согласно изобретению дополнительно введены ключевой элемент и блок формирования приращений от искомой переменной с предыдущих шагов по времени, выход которого соединен с одним из входов сумматора приращений, а вход – с выходом ключевого элемента, первый вход которого соединен с выходом интегратора, а второй служит входом для сигнала управления.
Рассмотрим в качестве примера дифференциальное уравнение с первой частной производной по времени:
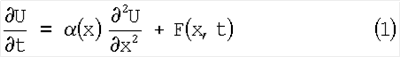
с начальными и граничными условиями:
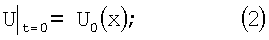
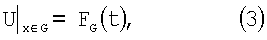
где U – искомая переменная,
t – время,
х – пространственная координата (в общем случае это может быть вектор),
U0(x) – начальные значения искомой переменной,
G – граница области решения,
F(x,t) – функция источника внутри области решения,
FG(t) – функция источника на границе области решения.
В соответствии с конечно-разностной аппроксимацией по неявной схеме исходного дифференциального уравнения получаем расчетную формулу для внутренних узлов сетки, наложенной на область решения:
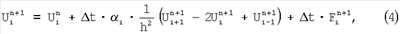
где  t – шаг по времени, t – шаг по времени,
h – шаг по пространственной координате,
n – номер шага по времени,
i – номер шага по пространственной координате.
Для обеспечения устойчивости решения при любом шаге по времени применяется метод установления (итераций) по фиктивному времени. Для этого все слагаемые конечно-разностного уравнения (4) переносятся в правую часть, а в левой части ноль заменяется производной от искомой переменной по фиктивному времени 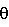 : :
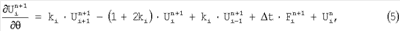
где 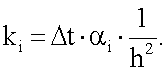
Далее применяется конечно-разностная аппроксимация по явной схеме для аргумента 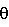 . .

где [ ] ]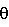 – правая часть уравнения (5). – правая часть уравнения (5).
На первом шаге (n=0) по реальному времени расчетное уравнение (6) имеет вид:
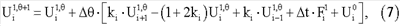
где 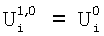 . .
В общем виде уравнение (7) для n+1-го шага по времени:
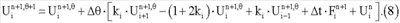
Результат на выходе ячейки (следящего интегратора) формируется в виде приращений в соответствии со следующей расчетной формулой, вытекающей из уравнения (8):
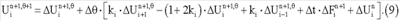
Результат вычислений на каждом шаге по времени (8) накапливается в интеграторе и через ключевой элемент после подачи разрешающего управляющего сигнала передается в блок формирования приращений от искомой переменной с предыдущих шагов по времени в промежутке между циклами интегрирования по 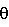 . В следующем цикле по . В следующем цикле по 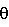 этот блок дает последнее слагаемое в уравнении (9) этот блок дает последнее слагаемое в уравнении (9) 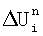 для вычисления выходного результата ячейки. для вычисления выходного результата ячейки.
Таким образом, введение дополнительных блока формирования приращений от искомой переменной с предыдущих шагов по времени и ключевого элемента позволяет расширить функциональные возможности ячейки и выполнять решение дифференциальных уравнений в частных производных не только по пространственным координатам, но и по времени.
Предлагаемая ячейка однородной структуры для решения дифференциальных уравнений в частных производных представлена на чертеже.
Она содержит блок масштабных интеграторов 1 (БМИ), сумматор приращений 2 (СП), следящий интегратор 3 (СИ), интегратор 4 (И), блок формирования приращений от искомой переменной с предыдущих шагов по времени 5 (БФПВ), ключевой элемент 6 (КЭ). Выходом ячейки для соединения со входами других ячеек однородной структуры является выход следящего интегратора 3 (СИ). Входы блока масштабных интеграторов 1 (БМИ) являются входами выходных сигналов других ячеек однородной структуры, а один из них соединен с собственным выходом ячейки. Еще один вход блока масштабных интеграторов 1 (БМИ) может быть использован для подачи значения приращения функции источника 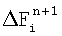 в выражении (9), которая может иметь сложный вид, и подается от внешнего устройства управления. Все выходы блока масштабных интеграторов 1 (БМИ) и выход блока формирования приращений от искомой переменной с предыдущих шагов по времени 5 (БФПВ) соединены со входами сумматора приращений 2 (СП), выход которого подключен ко входу следящего интегратора 3 (СИ). Выход следящего интегратора 3 (СИ) является выходом ячейки и соединен со входом интегратора 4 (И), выход которого через ключевой элемент 6 (КЭ) подключен (при наличии разрешающего сигнала на втором входе ключевого элемента) ко входу блока формирования приращений от искомой переменной с предыдущих шагов по времени 5 (БФПВ). в выражении (9), которая может иметь сложный вид, и подается от внешнего устройства управления. Все выходы блока масштабных интеграторов 1 (БМИ) и выход блока формирования приращений от искомой переменной с предыдущих шагов по времени 5 (БФПВ) соединены со входами сумматора приращений 2 (СП), выход которого подключен ко входу следящего интегратора 3 (СИ). Выход следящего интегратора 3 (СИ) является выходом ячейки и соединен со входом интегратора 4 (И), выход которого через ключевой элемент 6 (КЭ) подключен (при наличии разрешающего сигнала на втором входе ключевого элемента) ко входу блока формирования приращений от искомой переменной с предыдущих шагов по времени 5 (БФПВ).
Перечисленные элементы могут быть реализованы на базе цифровых интегральных микросхем, например, серии К500-К531 и др. (Нефедов А.В. Интегральные микросхемы и их зарубежные аналоги. Справочник. Т4, 2001). Блок формирования приращений от искомой переменной с предыдущих шагов по времени 5 (БФПВ) может быть реализован на базе масштабных интеграторов и логических элементов.
Ячейка однородной структуры работает следующим образом.
Начальное значение искомой переменной 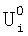 заносят предварительно в блок формирования приращений от искомой переменной с предыдущих шагов по времени 5 (БФПВ) в соответствии с начальным условием исходной задачи (2). Если ячейку используют в качестве граничной, то в блок 5 (БФПВ) заносят граничные условия в соответствии с выражением (3). заносят предварительно в блок формирования приращений от искомой переменной с предыдущих шагов по времени 5 (БФПВ) в соответствии с начальным условием исходной задачи (2). Если ячейку используют в качестве граничной, то в блок 5 (БФПВ) заносят граничные условия в соответствии с выражением (3).
После окончания цикла расчета по 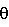 на первом шаге по времени по уравнению (7) на второй вход ключевого элемента 6 (КЭ) подают открывающий сигнал от внешнего устройства управления, и полученное значение искомой переменной из интегратора 4 (И) по уравнению (8) передается в блок формирования приращений от искомой переменной с предыдущих шагов по времени 5 (БФПВ) и используется в следующем цикле интегрирования по на первом шаге по времени по уравнению (7) на второй вход ключевого элемента 6 (КЭ) подают открывающий сигнал от внешнего устройства управления, и полученное значение искомой переменной из интегратора 4 (И) по уравнению (8) передается в блок формирования приращений от искомой переменной с предыдущих шагов по времени 5 (БФПВ) и используется в следующем цикле интегрирования по 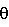 в качестве предыдущего значения на втором шаге по реальному времени (последнее слагаемое в уравнении 9). Длительность одного цикла интегрирования по фиктивному времени в качестве предыдущего значения на втором шаге по реальному времени (последнее слагаемое в уравнении 9). Длительность одного цикла интегрирования по фиктивному времени 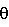 задают такой, чтобы значения искомой переменной в каждой ячейке устанавливались постоянными с точностью до заданной погрешности. задают такой, чтобы значения искомой переменной в каждой ячейке устанавливались постоянными с точностью до заданной погрешности.
Эту итерационную процедуру повторяют далее до тех пор, пока не закончится заданное время интегрирования (по индексу n). Итоговый результат вычислений накапливается в интеграторе 4 (И) в соответствии со следующей расчетной формулой, следующей из уравнения (8).
Формула изобретения
Ячейка однородной структуры для решения дифференциальных уравнений в частных производных, содержащая интегратор, блок масштабных интеграторов, выходы которого соединены со входами сумматора приращений, следящий интегратор, выход которого соединен со входом интегратора и с одним из входов блока масштабных интеграторов, а вход следящего интегратора подключен к выходу сумматора приращений, причем выходом ячейки для соединения с входами других ячеек однородной структуры является выход следящего интегратора, а входами ячейки для соединения с выходами других ячеек – входы блока масштабных интеграторов, отличающаяся тем, что в нее введены ключевой элемент и блок формирования приращений от искомой переменной с предыдущих шагов по времени, выход которого соединен с одним из входов сумматора приращений, а вход с выходом ключевого элемента, первый вход которого соединен с выходом интегратора, а второй служит входом для сигнала управления.
РИСУНКИ
|