Патент на изобретение №2355923

(54) ПЛАНЕТАРНЫЙ ЗУБЧАТЫЙ МЕХАНИЗМ С ДВОЙНЫМИ САТЕЛЛИТАМИ

(57) Реферат:

Изобретение относится к машиностроению и предназначено для использования в планетарных передачах с высоким передаточным отношением в одной ступени и при небольших габаритах. Планетарный механизм содержит корпус (18), водило, образованное двумя жестко связанными дисками (19 и 20), двойные сателлиты (3), каждое из которых состоит из двух одинаковых и повернутых друг относительно друга венцов (27, 28 и 29, 30) соответственно. Венцы (27, 28) сателлитов (3) находятся в зацеплении с ведущим центральным колесом (1) внешнего зацепления, также выполненным ступенчатым из двух одинаковых и повернутых друг относительно друга венцов (25, 26). Венцы (25 и 26) имеют один зуб с профилем в виде эксцентрично смещенной окружности. Венцы (27 и 28) сателлитов (3) имеют профиль циклоидальной формы, образуя эксцентриково-циклоидальное зацепление, которое имеет увеличенное в несколько раз передаточное отношение при прочих равных условиях. Венцы (29, 30) сателлитов (3) выполнены однозубыми в виде эксцентриков. Венцы (29, 30) взаимодействуют с венцами (31 и 32) второго центрального колеса внутреннего зацепления, которые выполнены на внутренней поверхности корпуса (18). Выполнение эксцентриково-циклоидального зацепления в обоих рядах планетарного механизма позволяет еще более увеличить его передаточное отношение без изменения габаритов. 1 з.п. ф-лы, 8 ил.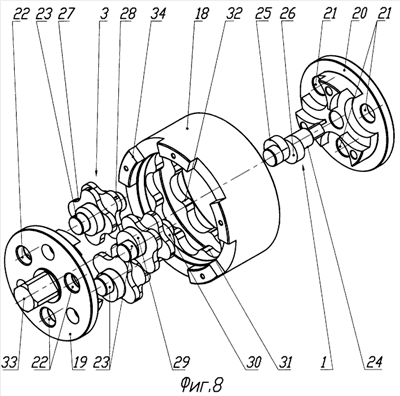

Изобретение относится к машиностроению, и предназначено для создания зубчатых планетарных передач вращения с высоким передаточным отношением в одной ступени, которые могут быть использованы в приводах самого широкого назначения, требующих высоких передаточных отношений при небольших габаритах.

Известен четырехзвенный планетарный механизм Джеймса (И.И. Артоболевский. Теория механизмов и машин. – М.: Наука, 1988, с.156). Устройство содержит два центральных зубчатых колеса, одно из которых имеет внешние, а другое – внутренние зубья, водило и сателлиты, зацепляющиеся одновременно с обоими центральными колесами. Центральное колесо внешнего зацепления установлено на ведущем валу, колесо внутреннего зацепления неподвижно, а водило соединено с ведомым валом. Передача имеет высокий кпд (97-98)% и достаточно простую конструкцию.

Основным недостатком этого механизма является невысокое передаточное отношение, определяемое как отношение радиусов центральных колес. Для увеличения передаточного отношения необходимо значительно увеличивать диаметр колеса внутреннего зацепления, что резко увеличивает габариты и массу передачи. На практике передаточное отношение механизма по этой схеме обычно выбирается в пределах 3-8.

Известен планетарный механизм Давида с внешним, внутренним или смешанным зацеплением (В.М.Шанников. Планетарные редукторы с внецентроидным зацеплением. – М.: Машгиз, 1948, с.4, а также А.Ф.Крайнев. Словарь-справочник по механизмам, М.: Машиностроение, 1987, с.290). Механизм содержит два центральных колеса: оба внешнего или оба внутреннего или одно внешнего, а другое – внутреннего зацепления. В водиле установлены двойные сателлиты, первые и вторые колеса которых зацепляются с соответствующими центральными колесами. Механизмы по схеме Давида позволяют получать высокие передаточные отношения только при достаточно больших габаритах.

Для увеличения передаточного отношения при небольших габаритах в планетарной передаче по патенту RU 2270388 используют схему Давида с внешним зацеплением и дополнительные паразитные шестерни. При этом происходит усложнение конструкции и удорожание передачи.

Известны также более сложные схемы планетарных передач, соединяющие два или более простейших планетарных механизма (А.Ф.Крайнев, Словарь-справочник по механизмам. М.: Машиностроение, 1987, с.290-291). Соответственно усложняется конструкция передачи, уменьшается ее кпд.

За прототип изобретения выбираем описанный выше планетарный механизм по схеме Давида. Планетарный механизм содержит водило, двойные сателлиты и два центральных колеса. Каждое из центральных колес находится в зацеплении соответственно с первыми или вторыми колесами двойных сателлитов и образует первый и второй ряды эвольвентного зацепления. Центральные колеса могут быть оба внешнего зацепления или одно внешнего, а другое – внутреннего (смешанного) зацеплений. Механизм по схеме Давида с внешним зацеплением для больших передаточных отношений имеет очень низкий КПД (менее 0,2% при передаточном отношении 10000 по оценке в книге В.М.Шанников. Планетарные редукторы с внецентроидным зацеплением. – М.: Машгиз, 1948, с.4), а механизм со смешанным зацеплением позволяет получить при достаточно высоком кпд передаточное отношение только в пределах 8-15.

Таким образом, задачей изобретения является создание простой планетарной передачи, обладающей высоким кпд и высоким передаточным отношением. Технический результат, достигаемый изобретением, заключается в увеличении передаточного отношения в планетарной передаче без увеличения ее габаритов. Дополнительным результатом является повышение нагрузочной способности передачи при прочих равных условиях.

Для решения поставленной задачи планетарный зубчатый механизм с двойными сателлитами, как и прототип, содержит водило, два центральных колеса, находящихся в зацеплении соответственно с первыми и вторыми колесами двойных сателлитов и образующих два ряда зацепления. В отличие от прототипа, по меньшей мере, в одном ряду зацепления меньшие колеса выполнены однозубыми, с профилем зуба в виде эксцентрично смещенной окружности. Колеса большего диаметра в этом ряду выполнены с зубьями циклоидального профиля, образуя эксцентриково-циклоидальное (ЭЦ) зацепление. Число венцов сателлитов в ряду ЭЦ зацепления должно быть не менее трех. Второй ряд зацепления в этом механизме может быть образован колесами с обычными эвольвентными профилями зубьев.

Колеса, по меньшей мере, одного из рядов эксцентриково-циклоидального зацепления целесообразно выполнить ступенчатыми, составленными из двух и более одинаковых зубчатых венцов, повернутых друг относительно друга на угол, равный угловому шагу венца, деленному на число венцов. Т.е. для однозубого ступенчатого колеса с двумя венцами каждый из венцов будет представлять собой эксцентрично смещенную окружность, причем окружности будут повернуты друг относительно друга на 180 градусов (угловой шаг равен 360 градусам, а число зубчатых венцов равно 2).

В этом случае второй ряд зацепления может быть также выполнен экцентриково-циклоидальным, что еще более увеличивает передаточное отношение механизма при прочих равных условиях. Т.е. меньшие колеса второго ряда выполняются однозубыми с профилем зуба в виде эксцентрично смещенной окружности, а находящиеся с ними в зацеплении большие колеса выполнены с зубьями циклоидального профиля.

Для повышения равномерности передачи вращения зубчатые колеса обоих рядов эксцентриково-циклоидального зацепления выполняются ступенчатыми из одинаковых и повернутых друг относительно друга венцов.

Центральные колеса в рядах могут быть внешнего зацепления или смешанного зацепления, т.е. в одном ряду центральное колесо имеет внешнее зацепление, а в другом ряду – внутреннее зацепление. Механизм, у которого второе центральное колесо выполнено с внутренним зацеплением, имеет более высокий кпд и может обеспечить большее передаточное отношение.

Изобретение иллюстрируется графическими материалами, где на фиг.1 и 2 изображены схемы планетарных механизмов внешнего и смешанного зацеплений соответственно. На фиг.3 и 4 показаны профили колес для схем на фиг.1 и 2 соответственно, которые в одном ряду имеют обычное эвольвентное зацепление, а в другом ряду зацепление в соответствии с изобретением выполнено эксцентриково-циклоидальным. На фиг.5 показано эксцентриково-циклоидальное зацепление ступенчатых колес. На фиг.6 и 7 на одном виде совмещены профили колес эксцентриково-циклоидального зацепления в обоих рядах для механизмов по схемам фиг.1 и 2 соответственно. На этих фигурах колеса в одном из рядов зацепления выполнены ступенчатыми. На фиг.8 в качестве примера представлена конструкция редуктора для усилителя крутящих моментов, выполненного по схеме на фиг.2 и имеющего в обоих рядах эксцентриково-циклоидальное зацепление ступенчатых колес.

Планетарный зубчатый механизм на фиг.1 содержит два центральных колеса 1 и 2 внешнего зацепления и двойные сателлиты 3, посаженные в водиле 4. Первые колеса 6 двойных сателлитов 3 и центральное колесо 1, находящееся с ними в зацеплении, образуют первый ряд зацепления. Вторые колеса 7 двойных сателлитов 3 вместе со вторым центральным колесом 2 образуют второй ряд зацепления. В первом ряду колесо 1 и колеса 6 имеют обычное зацепление, образованное эвольвентными зубьями 5 и 8 (см. фиг.3). Венцы 9 вторых колес 7 сателлитов 3 во втором ряду зацепления выполнены однозубыми с профилем в виде эксцентрично смещенных окружностей. Второе центральное колесо 2 имеет циклоидальный зубчатый венец 10. Назовем такой вид зацепления эксцентриково-циклоидальным. Число венцов сателлитов в ряду эксцентриково-циклоидального зацепления должно быть не меньше трех. Действительно, обращаясь к фиг.3, мы видим, что только в этом случае в фазе входа в зацепление находятся одновременно один или два однозубых эксцентриковых венца 9. При меньшем количестве венцов сателлитов будут иметь место такие положения этих венцов, когда все венцы 9 будут находиться в фазе выхода из зацепления с циклоидальным венцом 10 центрального колеса 2, и вращение от сателлитов 3 к колесу 2 передаваться не будет. В механизме, иллюстрируемом фиг.3, число венцов сателлитов в ряду зацепления равно числу сателлитов. Однако, если колеса в зацеплении выполнить ступенчатыми из нескольких одинаковых повернутых друг относительно друга венцов, то число сателлитов будет меньше, чем число венцов, и работоспособным может быть механизм с двумя или даже с одним сателлитом. Это будет более подробно показано и описано ниже при обсуждении фиг.5. Представленный на фиг.1 и 3 планетарный механизм является дифференциальным, так как все его три основных звена (центральные колеса 1 и 2 и водило 4) подвижны. Для того чтобы получить механическую передачу, одно из этих звеньев следует сделать неподвижным. В зависимости от выбора неподвижного звена и ведущего и ведомого звеньев передача будет иметь разные передаточные отношения и может являться как мультипликатором, так и редуктором.

При ведущем колесе 1, ведомом колесе 2 и неподвижном водиле 4 передаточное отношение механизма по схеме Давида определяется как i₁₂=Z₆/Z₁·Z₂/Z₇, и так как для эксцентриково-циклоидального зацепления Z₇=1, то i₁₂=Z₆·Z₂/Z₁, и для реальной конструкции на фиг.1, 3 i₁₂ составляет 23,5. В случае ведомого водила 4 и неподвижного колеса 2 передаточное отношение будет определяться как i₁₄=1-Z₆·Z₂/Z₁=-22,5. Таким образом, передаточное отношение предлагаемого механизма теоретически в Z₇ раз больше, чем у механизма с обычным эвольвентным зацеплением в обоих рядах. Следует отметить, что для редуктора эвольвентный ряд лучше выполнить на входе, так как эксцентриково-циклоидальное зацепление имеет большие предельно-допустимые моменты вращения. Действительно, в эксцентриково-циклоидальном зацеплении взаимодействуют выпуклый профиль зуба – эксцентричной окружности 9 с вогнутым профилем циклоидального зуба 10, что повышает их контактную прочность при прочих равных условиях. Кроме того, для обеспечения одного и того же передаточного отношения большие колеса в ряду ЭЦ зацепления будут иметь значительно меньшее число зубьев, чем для эвольвентного зацепления, что при одинаковых размерах колес еще более увеличивает нагрузочную способность.

В планетарном механизме, изображенном на фиг.2 и 4, одно из центральных колес, а именно колесо 11 имеет внутреннее зацепление со вторыми колесами 7 двойных сателлитов 3. Это колесо имеет внутренний венец 12 циклоидальной формы. Все остальные элементы механизма такие же, как и на фиг.1 и 3, и имеют те же обозначения. Такая схема для обычных эвольвентных колес дает передаточное отношение не более 15. В нашем же случае при неподвижном водило 4 и ведомом центральном колесе 11 передаточное отношение механизма составляет i_1/11=-Z₆/Z₁·Z₁₁/Z₇=-Z₆·Z₁₁/Z₁, т.к. Z₇=1. В реальной конструкции для Z₁=20, Z₆=47 и Z₁₁=11 i_1/11=-25,85. При ведомом водиле 4 и неподвижном центральном колесе 10 передаточное отношение определяется выражением i_1/4=1+Z₆·Z₁₁/Z₁ и при тех же значениях Z₁, Z₆ и Z₁₁ составит i_1/4=26, 85, что значительно выше возможных значений для обычного механизма с эвольвентным зацеплением колес.

Для повышения равномерности вращения колес и равномерности передачи момента целесообразно колеса с эксцентриково-циклоидальным зацеплением выполнять ступенчатыми, как это показано на фиг.5 для эксцентриково-циклоидального зацепления колес в первом ряду. Центральное однозубое колесо 1 выполнено ступенчатым, т.е. составлено из двух одинаковых венцов 14 и 15, имеющих форму эксцентрично смещенных в противоположные стороны окружностей, что аналогично их повороту друг относительно друга на 180 градусов. Угол поворота определяется как угловой шаг однозубого колеса 1 (360 градусов), деленный на число венцов ступенчатого колеса (число венцов 2). Каждый из венцов 14 и 15 ступенчатого колеса 1 взаимодействует соответственно с циклоидальными венцами 16 и 17 ступенчатых колес 6 сателлитов 3. Венцы 16 и 17 повернуты друг относительно друга на половину углового шага. Для колес на фиг.5 этот угол составляет 18 градусов.

При вращении колеса 1 по часовой стрелке венец 14 находится в фазе вхождения в зацепление с венцами 16 верхнего и левого сателлитов, а венец 15 – с венцом 17 – правого сателлита 3. В результате в передаче момента вращения участвуют одновременно три венца трех сателлитов, что повышает равномерность передачи момента. Очевидно, что механизм со ступенчатыми колесами будет работоспособным и с двумя сателлитами, так как в любом положении колеса будут иметь, по меньшей мере, пару венцов, находящихся в фазе входа в зацепление при общем числе венцов сателлитов в этом ряду, равном 4.

Для еще большего увеличения передаточного отношения можно зацепление обоих рядов выполнить эксцентриково-циклоидальным (см. фиг.6 и 7). Фиг.6 соответствует схеме на фиг.1 с колесами внешнего зацепления. Первый ряд зацепления выполнен со ступенчатыми колесами, так как это показано на фиг.5. Центральное колесо 1 внешнего зацепления 1 выполнено ступенчатым из двух одинаковых венцов 14 и 15. Венцы представляют собой эксцентрично смещенные от центра колеса окружности, повернутые друг относительно друга на половину углового шага, так как венцов в колесе 2. Угол поворота составляет 180 градусов, т.е. венцы 14 и 15 это эксцентрично смещенные в противоположные стороны окружности. Первые колеса 6 сдвоенных сателлитов 3 выполнены также ступенчатыми из одинаковых повернутых друг относительно друга циклоидальных венцов 16 и 17. Угол поворота этих венцов друг относительно друга составляет также половину углового шага, и для 10 зубьев угол поворота равен 18 градусам. Венец 14 колеса 1 находится в зацеплении с венцами 16 колес 3, а венец 15 зацепляется с венцами 17 соответствующих колес. Эксцентриково-циклоидальное зацепление во втором ряду выполнено таким же, как показано на фиг.3, и его элементы обозначены аналогично. Т.е. венцы 9 вторых колес 7 сателлитов выполнены в виде эксцентрично смещенных окружностей, а венец 10 центрального колеса внешнего зацепления 2 выполнен циклоидальным.

Фиг.7 показывает эксцентриково-циклоидальные зацепления в обоих рядах механизма, выполненного по схеме на фиг.2. Здесь также колеса в первым ряду зацепления выполнены ступенчатыми, как это показано на фиг.5. Отличие фиг.7 от фиг.6 составляет лишь центральное колесо 11 во втором ряду, которое выполнено с циклоидальным профилем 12 внутреннего зацепления. Остальные обозначения на фиг.7 соответствуют обозначениям фиг.6.

Рассмотрим конкретную конструкцию планетарного механизма на фиг.8, предназначенного для работы в качестве усилителя крутящего момента (гайковерта). В цилиндрическом корпусе 18 установлены фланцевые диски 19 и 20, жестко связанные друг с другом стяжными винтами (на фигуре не показанными). Диски 19 и 20 образуют водило планетарного механизма. В отверстиях 21 и 22 дисков 19 и 20 на осях 23 установлены три сателлита 3. Центральное колесо 1 является ведущим звеном и выполнено за одно целое с ведущим валом 24. Колесо 1 выполнено ступенчатым из двух одинаковых венцов 25 и 26, представляющих собой эксцентрично смещенные в разные стороны от центра колеса окружности. Венцы 25 и 26 находятся в зацеплении с одинаковыми циклоидальными венцами 27 и 28, которые являются ступенчатыми колесами первых колес двойных сателлитов 3. Вторые колеса сателлитов 3 выполнены также ступенчатыми, образованными двумя одинаковыми венцами в виде эксцентрично смещенных в противоположные стороны окружностей 29 и 30. Для того чтобы избежать консольной нагрузки на оси 23, эти венцы разнесены в пространстве вдоль оси и расположены по обе стороны от венцов 27, 28 первых колес сателлитов. Второе центральное колесо внутреннего зацепления выполнено также ступенчатым на внутренней поверхности корпуса 18 и представляет собой два разнесенных вдоль оси одинаковых и повернутых друг относительно друга циклоидальных профиля 31 и 32. Ведомым звеном является водило, с диском 19 которого жестко связан квадрат 33 для съемной головки гайковерта. Корпус 18 имеет торцевые шлицы 34, которыми он крепится к неподвижным элементам для отбора реактивного момента. Передаточное отношение редуктора гайковерта равно i=1+Z₂₇Z₃₁=33, где Z₂₇ и Z₃₁ числа зубьев циклоидальных венцов 27 сателлитов 3 и циклоидальных венцов 31 центрального колеса внутреннего зацепления.

Следует отметить, что при выборе в конкретном механизме опорного, ведущего и ведомого звеньев следует руководствоваться следующими соображениями. Если для достижения заданного передаточного отношения достаточно выполнить с эксцентриково-циклоидальным зацеплением только один ряд механизма, то обычное эвольвентное зацепление следует выполнить со стороны ведущего звена, как это было уже показано выше. При необходимости выполнения эксцентриково-циклоидальным зацепления в обоих рядах ряд зацепления со стороны ведущего звена следует выполнять из ступенчатых колес.

Рассмотрим работу предлагаемых механизмов, выполненных по схеме на фиг.1 в качестве редукторов с ведущим звеном – центральным колесом внешнего зацепления 1 и неподвижным водилом 4. Пусть колесо 1 с эвольвентным зацеплением вращается по часовой стрелке, как это показано на фиг.3 и 4. Первые колеса 6 сателлитов 3 будут вращаться в противоположную сторону с передаточным отношением, определяемым отношением чисел зубьев венцов 8 и 5. Одновременно с колесами 6 будут поворачиваться и вторые колеса 7 этих же сателлитов, представляющие собой эксцентрично смещенные окружности 9. При этом венцы 9 верхнего и левого сателлитов находятся в фазе входа в зацепление с циклоидальным профилем 10 центрального колеса 2 и обеспечивают его поворот в направлении, совпадающем с направлением вращения входного колеса 1 с передаточным отношением, равным Z₆·Z₂/Z₁.

Работа механизма, выполненного по схеме на фиг.2 и изображенного на фиг.4, происходит аналогичным образом, только передаточное отношение будет определяться как – Z₆·Z₁₁/Z₁, т.е. ведомое колесо 11 будет вращаться в противоположную сторону. Рассмотрим работу механизмов с двумя рядами эксцентриково-циклоидального зацепления на фиг.6 и 7 в режиме редуктора. Ведущим звеном в этом режиме может быть либо водило 4, либо центральное колесо внешнего зацепления 1. Примем ведущим звеном колесо 1. При его вращении по часовой стрелке венец 14 будет находиться в фазе входа в зацепление с венцами 16 верхнего и левого сателлитов 3, вращая их против часовой стрелки. Второй венец 15 ступенчатого колеса 1 в то же самое время самое время будет находиться в силовом зацеплении с венцами 17 левого и правого сателлитов. Таким образом, в первом ряду зацепления поток мощности будет передаваться через все три сателлита. Вращение сателлитов 3 против часовой стрелки означает одновременное вращение вторых колес 7 сателлитов. При этом венцы 9 этих колес будут находиться в фазе входа в зацепление с циклоидальным венцом 10 только для левого и верхнего сателлитов. Сателлиты, входящие в зацепление, поочередно меняются, однако в любой момент времени, по меньшей мере, один сателлит участвует в передаче вращения к центральному колесу 2. Колесо 2 вращается в том же самом направлении, что и ведущее колесо 1. Передаточное отношение в схеме определяется как Z₆·Z₂, что в Z₁ раз выше, чем для редуктора с одним рядом эксцентриково-циклоидального зацепления на фиг.3. Если в качестве ведущего звена выбрать водило 4, то передаточное отношение будет равно 1-Z₂·Z₆.

Работа редуктора на фиг.7 будет отличаться только противоположным направлением вращения ведомого колеса 11 и величиной передаточного отношения, которое будет определяться как – Z₆·Z₁₁, т.е. также будет в Z₁ раз выше, чем у редуктора с одним рядом эксцентриково-циклоидального зацепления на фиг.4.

Усилитель крутящих моментов на фиг.8 работает следующим образом. Ведущий вал 24 вращает центральное колесо 1 с двумя одинаковыми однозубыми венцами 25 и 26 в виде эксцентрично смещенных окружностей. Вращение передается на циклоидальные венцы 27 и 28 сателлитов 3 с числом зубьев 4. Сателлиты 3 вращаются совместно с венцами 29 и 30 вторых колес сателлитов. Венцы 29 и 30 имеют один зуб с профилем в виде эксцентрично смещенной окружности. При обкатывании этими венцами циклоидальных венцов 31 и 32 неподвижного корпуса 18 начинает поворачиваться водило, образованное дисками 19 и 20. Водило является ведомым звеном. Передаточное отношение усилителя крутящих моментов составляет 33.

Формула изобретения

1. Планетарный зубчатый механизм с двойными сателлитами, содержащий водило, два центральных колеса, каждое из которых зацепляется соответственно с первыми и вторыми колесами двойных сателлитов, образуя два ряда зацепления, отличающийся тем, что, по меньшей мере, в одном из рядов зацепление выполнено эксцентриково-циклоидальным, в котором меньшие колеса выполнены однозубыми, с профилем зуба в виде эксцентрично смещенной окружности, а находящиеся с ними в зацеплении колеса большего диаметра выполнены с зубьями циклоидального профиля, причем число венцов сателлитов в этом ряду составляет не менее трех.

2. Планетарный зубчатый механизм по п.1, отличающийся тем, что колеса, по меньшей мере, одного из рядов с эксцентриково-циклоидальным зацеплением выполнены ступенчатыми, образованными, по меньшей мере, двумя одинаковыми зубчатыми венцами, повернутыми относительно друг друга на угол, равный угловому шагу зубьев, деленному на число зубчатых венцов ступенчатого колеса.

РИСУНКИ