|
|
(21), (22) Заявка: 2006134696/28, 01.04.2005
(24) Дата начала отсчета срока действия патента:
01.04.2005
(30) Конвенционный приоритет:
03.04.2004 GB 0407699.8
(43) Дата публикации заявки: 10.05.2008
(46) Опубликовано: 20.03.2009
(56) Список документов, цитированных в отчете о
поиске:
SU 1666981 A1, 30.07.1991. SU 1497587 A1, 30.07.1989. WO 03/048812 A1, 12.06.2003. US 2003/050759 A1, 13.03.2003. US 6700526 A, 02.03.2004.
(85) Дата перевода заявки PCT на национальную фазу:
03.11.2006
(86) Заявка PCT:
EP 2005/051480 (01.04.2005)
(87) Публикация PCT:
WO 2005/096019 (13.10.2005)
Адрес для переписки:
191186, Санкт-Петербург, а/я 230, “АРС-ПАТЕНТ”, пат.пов. М.В.Хмаре, рег. № 771
|
(72) Автор(ы):
РЕСТЕН Таге (NO),
АМУНДСЕН Лассе (NO)
(73) Патентообладатель(и):
СТАТОЙЛ АСА (NO)
|
(54) СПОСОБ И УСТРОЙСТВО ДЛЯ ОБРАБОТКИ ЭЛЕКТРОМАГНИТНЫХ ДАННЫХ
(57) Реферат:
Изобретение относится к определению диаграммы направленности излучения электромагнитного источника и применению полученных данных, например, при электромагнитном профилировании морского дна. Сущность: измеряют на, по меньшей мере, одном детекторе электрические и магнитные поля, создаваемые, по меньшей мере, одним источником. Составляют поверхностный интеграл по измеренным данным, взвешенным с использованием функции Грина и ее пространственных производных. Вычисляют поверхностный интеграл в, по меньшей мере, одном пункте с целью определения диаграммы направленности излучения в указанном пункте от, по меньшей мере, одного источника. Удаляют диаграмму направленности излучения источника из измеренных электромагнитных данных. 2 н. и 26 з.п. ф-лы, 6 ил.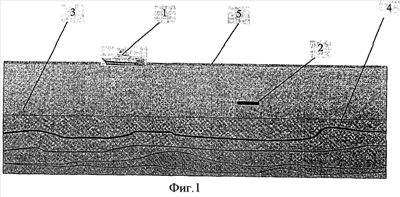
Область техники, к которой относится изобретение
Настоящее изобретение относится к способам определения диаграммы направленности излучения электромагнитного источника и применению полученных данных. Настоящее изобретение может быть использовано, например, при определении диаграммы направленности излучения источника, связанной с известными или неизвестными источниками при электромагнитном профилировании морского дна.
Уровень техники
Технология электромагнитного профилирования морского дна (EM-SBL) является новым средством изучения углеводородов, основанным на электромагнитных данных, она раскрыта в статье Eidesmo и др. (2002) «Профилирование морского дна, новый метод прямой идентификации удаленных содержащих углеводороды отложений на глубоководных площадях», The Leading Edge, 20, №3, 144-152 и Ellingsrud и др. (2002) «Обнаружение удаленных гидрокарбонатных залежей при помощи профилирования морского дна: результаты работ в прибрежной зоне Анголы», First Break, 21, №10, 972-982. EM-SBL является особым видом применения электромагнитного зондирования с управляемым источником (CSEM). CSEM-зондирование много лет с успехом используется для изучения океанических бассейнов и активных спрединговых центров. SBL является первым применением CSEM для дистанционного и прямого обнаружения углеводородов в морской среде. Два первых опубликованных успешных SBL исследований были проведены в прибрежной зоне Западной Африки (упомянутые выше Eidesmo и др. и Ellingsrud и др.) и в прибрежной зоне средней Норвегии, Resten и др. (2003) «Исследования профиля рельефа в районе газового месторождения Ормен Ланге», EAGE, 65th An. Internat. Mtg., Eur. Assoc. Geosc. Eng., Extended Abstracts, P058. Оба исследования проводились в глубоководной среде (на глубине более 1000 метров).
Этот метод использует горизонтальный электрический дипольный источник (HED), который излучает низкочастотный электромагнитный сигнал в морское дно и вниз в подстилающие отложения. Электромагнитная энергия быстро затухает в проводящих глубинных отложениях вследствие заполненного водой порового пространства. В породах с высоким сопротивлением, таких как заполненные гидрокарбонатами песчаники, и при критических углах падения энергия распространяется вдоль слоев и ослабляется в меньшей степени. Энергия преломляется обратно к морскому дну и выделяется расположенными там электромагнитными приемниками. Когда расстояние приемник-источник (т.е. офсет) приблизительно в 2-5 раз больше глубины резервуара, преломленная энергия от слоев с высоким сопротивлением будет превышать прямо распространяющуюся энергию. Выделение распространяющейся вдоль слоев и преломленной энергии является основой EM-SBL.
Мощность заполненного гидрокарбонатами резервуара должна быть не менее 50 м, чтобы обеспечить эффективное прохождение энергии вдоль пластов с высоким сопротивлением, и толща воды в идеальном случае должна быть более 500 м для предотвращения наложения волн-спутников от границы с воздухом.
Электромагнитная энергия, которая генерируется источником, распространяется во всех направлениях, и электромагнитная энергия быстро ослабевает в проводящих подводных отложениях. Расстояние, на которое энергия может проникать в глубинные породы, определяется, главным образом, мощностью и частотой возбуждаемого сигнала, а также проводимостью подстилающих формаций. Более высокие частоты приводят к большему ослаблению энергии и, соответственно, к меньшей глубине проникновения. Поэтому частоты, применяемые в EM-SBL, очень низкие, обычно 0,25 Гц. Диэлектрической проницаемостью можно пренебречь вследствие очень низких частот, магнитная проницаемость предполагается равной проницаемости в вакууме, т.е. соответствующей немагнитным глубинным породам.
В численном выражении заполненный углеводородами резервуар обычно имеет сопротивление в несколько десятков ом-метров или больше, тогда как сопротивление выше- и нижележащих осадков обычно менее нескольких ом-метров. Скорость распространения зависит от среды. В морской воде скорость приблизительно равна 1700 м/с (при частоте 1 Гц и сопротивлении 0,3 Ом·м), тогда как обычно скорость распространения магнитного поля в заполненных водой подводных осадках составляет около 3200 м/с при частоте 1 Гц и сопротивлении 1 Ом·м. Электромагнитное поле в заполненных углеводородом слоях с высоким сопротивлением распространяется со скоростью около 22000 м/с (при сопротивлении 50 Ом·м и частоте 1 Гц). Глубина электромагнитного проникновения для этих трех случаев составляет приблизительно 275 м, 500 м и 3600 м, соответственно.
Электромагнитные приемники могут быть размещены по отдельности на дне моря, каждый приемник измеряет две ортогональные горизонтальные и одну вертикальную компоненты как электрического, так и магнитного полей. HED источник состоит из двух электродов, разнесенных приблизительно на 200 м друг от друга и имеющих электрический контакт с морской водой. Источник передает непрерывный и периодически изменяющийся токовый сигнал с основной частотой в диапазоне 0,05-10 Гц. Двойная амплитуда АС изменяется от нуля до нескольких сотен ампер. Высота источника относительно морского дна должна быть значительно меньше глубины проникновения электромагнитной энергии в морской воде для обеспечения хорошей передачи возбуждаемого сигнала в глубинные отложения, например 50-100 м. Существует несколько способов размещения приемников на морском дне. Обычно приемники располагаются по прямой линии. При исследованиях может использоваться несколько таких линий, и линии могут иметь любую ориентировку относительно друг друга.
Окружающая обстановка и оборудование для регистрации EM-SBL данных иллюстрируются на фиг.1. Исследовательский корабль 1 буксирует электромагнитный источник 2 вдоль и перпендикулярно линиям приемников 3. Приемниками может регистрироваться как линейная (поперечная магнитная), так и широкополосная (поперечная электрическая) энергии. Приемники на морском дне 4 производят непрерывную запись сигналов во время буксировки источника со скоростью 1-2 узла. Выборка EM-SBL данных от источника производится с высокой плотностью, обычно с интервалом в 0,04 секунды. Данные от приемников должны считываться в соответствии с теоремой отсчетов (см., например, Antia (1991), «Вычислительные методы для научных работников и инженеров» Tata McGraw-Hill Publ. Co. Limited, Нью-Дели).
EM-SBL данные регистрируются в виде временных рядов и затем обрабатываются с использованием оконного Фурье анализа дискретных рядов (см., например, Jacobson и Lyons (2003) «Скользящее DFT», IEEE Signal Proc. Mag., 20, №2, 74-80) на передаваемой частоте, т.е. на основной частоте или ее гармонической составляющей. После обработки данные могут быть воспроизведены в виде графиков зависимости амплитуды от офсета (MVO) или фазы от офсета (PVO).
Электромагнитный источник, использующийся при EM-SBL съемках, может рассматриваться как активный источник. Другие пассивные источники также могут быть выделены, например магнитотеллурические источники, связанные с активностью солнечных пятен. Общее падающее электромагнитное поле, сформированное как активными, так и пассивными источниками, включающее также эффект влияния поверхности моря, известно как диаграмма направленности излучения источника. Проблема расшифровки диаграммы направленности излучения, связанной с известными и неизвестными источниками, расположенными над приемниками, является известной задачей. Хотя аналогичные технологии известны в акустических и сейсмических исследованиях, они не могут быть применены при проведении электромагнитных исследований, поскольку электромагнитные поля по своей природе отличаются от акустических и сейсмических полей.
Раскрытие изобретения
Согласно первому аспекту изобретения предлагается способ, охарактеризованный в пункте 1 формулы.
Другие аспекты и варианты реализации изобретения определены в других пунктах формулы.
Таким образом, можно создать технологию, которая позволяет улучшить определение диаграммы направленности излучения электромагнитного источника для произвольной формы Земли. Технология не требует каких-либо данных о внутреннем строении Земли в исследуемом районе, а также какой-либо информации о природе источников, а необходимы только измерения электрического и магнитного полей.
Краткое описание чертежей
Для лучшего понимания настоящего изобретения, а также чтобы показать, как оно может быть осуществлено на практике, в качестве примера будут описаны предпочтительные варианты изобретения со ссылкой на сопроводительные чертежи, где:
фиг.1 иллюстрирует окружающую среду и оборудование для получения ЕМ-SBL данных;
фиг.2 иллюстрирует идеализированный слой водного полупространства в соответствии с вариантом предложенного способа;
фиг.3 и 4 являются копиями фиг.1 и 2 с наложенной геометрией в соответствии с вариантом предложенного способа;
фиг.5 является блок-схемой, иллюстрирующей вариант способа в соответствии с изобретением;
фиг.6 является блок-схемой устройства для осуществления способа согласно изобретению.
Осуществление изобретения
Описанная здесь технология заимствует интегральное представление электромагнитных данных для определения диаграммы направленности излучения источника. Может быть также использована другая технология, например электромагнитный принцип взаимности (А.Т. deHoop, Справочник по излучению и рассеянию волн, Academic Press, 1995) или анализ уравнений Максвелла в области частота-волновое число. Независимо от используемой технологии, общий способ включает составление поверхностного интеграла по измеренным электромагнитным данным, взвешенным с использованием функции Грина и ее пространственных производных для идеализированного состояния. Поверхностный интеграл может быть вычислен в любом пункте, расположенном на или ниже плоскости или линии измерений, с целью прямого определения волнового поля источника в этом положении.
Интегральное представление увязывает свойства электромагнитной волны, характеризующейся двумя допустимыми «состояниями», которые могут появиться в данном пространственном объеме. Ниже описывается способ получения интегрального представления. Согласно интегральному представлению одним из двух допустимых состояний может быть реальная физическая электромагнитная обстановка. Другое состояние обычно устанавливается как отличающееся физическое состояние или идеализированное состояние, но в том же объеме. Обобщенная форма интегрального представления устанавливает взаимосвязь между этими двумя независимыми состояниями.
В соответствии с вариантом настоящего изобретения первым состоянием интегрального представления является физическая ситуация, которая будет описана здесь как физическая морская электромагнитная съемка, т.е. EM-SBL исследования, проиллюстрированные на фиг.1, которые проводятся над неизвестной средой, ограниченной сверху водным слоем. Источники расположены в том же месте над приемниками. Приемники располагаются в этом же месте внутри водного слоя и могут находится, например, внутри водной толщи или непосредственно контактировать с морским дном. Приемники записывают диаграмму направленности излучения от источника (источников), а также поле, создаваемое глубинными отложениями. Падающее волновое поле включает, по определению, волны, отраженные и преломленные на поверхности водного слоя.
Свойства волнового поля, создаваемого источниками над приемниками, зависят только от свойств водного слоя и границы раздела воздух-вода. Это искомое волновое поле, которое необходимо извлечь из зарегистрированных данных.
Вторым состоянием интегрального представления выбирается идеализированная электромагнитная съемка, которая производится в водном полупространстве, ограниченном сверху границей раздела воздух-вода, в соответствии с фиг.2. На чертежах одинаковые числовые значения представляют одинаковые свойства. Фиг.2 аналогична фиг.1 во всех отношениях, за исключением того, что на ней отсутствует морское дно; приемники 3 не располагаются на физической поверхности. В идеализированной съемке данные, записанные приемниками, будут содержать информацию только о падающем волновом поле от источника. Для решения этой проблемы водное полупространство во втором состоянии должно иметь одинаковые физические свойства с водным слоем в первом состоянии.
Интегральное представление устанавливает взаимосвязь между двумя описанными состояниями и позволяет определить диаграмму направленности излучения источника по измеренным реальным данным.
При дальнейшем описании будут приняты следующие обозначения:
Е=Е(х,  ) ) |
Напряженность электрического поля |
Н=Н(х,  ) ) |
Напряженность магнитного поля |
J=J(x,  ) ) |
Объемная плотность электрического тока |
K=K(х,  ) ) |
Объемная плотность магнитного потока |
F=F(x,  ) ) |
Объемная плотность силы 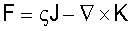 |
 = = (х) (х) |
Электрическая проводимость |
 = = (х) (х) |
Диэлектрическая проницаемость |
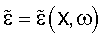 |
Комплексная диэлектрическая проницаемость 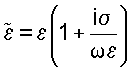 |
 = = (x) (x) |
Магнитная проницаемость |
 = = (x, (x,  ) ) |
Поперечная проводимость на единицу длины среды 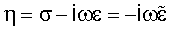 |
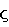 = =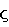 (х, (х,  ) ) |
Продольный импеданс на единицу длины среды 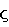 =-i =-i  |
с=с(х,  ) ) |
Комплексная скорость 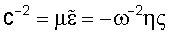 |
где  является угловой скоростью. Волновое число k определяется формулой является угловой скоростью. Волновое число k определяется формулой
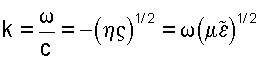
Токи проводимости и токи смещения объединены в формуле для комплексной диэлектрической проницаемости 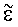 . Для EM-SBL записей токи смещения значительно меньше токов проводимости. Поэтому для расшифровки диаграммы направленности излучения EM-SBL . Для EM-SBL записей токи смещения значительно меньше токов проводимости. Поэтому для расшифровки диаграммы направленности излучения EM-SBL 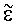 может быть аппроксимировано может быть аппроксимировано 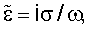 которое не зависит от диэлектрической проницаемости. Кроме того, магнитная проницаемость принимается равной которое не зависит от диэлектрической проницаемости. Кроме того, магнитная проницаемость принимается равной  = = 0=4 0=4 ·10-7 Гн/м, представляющей немагнитный водный слой. Комплексная скорость может быть затем представлена в виде с=( ·10-7 Гн/м, представляющей немагнитный водный слой. Комплексная скорость может быть затем представлена в виде с=( /( /( 0 0 ))1/2е-i ))1/2е-i /4. В процессе EM-SBL анализа диаграммы направленности излучения волновое число k можно записать в виде k=(i /4. В процессе EM-SBL анализа диаграммы направленности излучения волновое число k можно записать в виде k=(i  0 0 )1/2. Продольный импеданс на единицу длины равен )1/2. Продольный импеданс на единицу длины равен 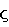 =-i =-i  0. 0.
Векторная теорема Грина
Теперь может быть определена интегральная взаимосвязь между двумя векторными полями, характеризующими два различных состояния внутри объема V. Это соотношение известно также как обратная теорема векторной теоремы Грина.
Объем V ограничен поверхностью S с направленными наружу нормальными векторами n. Два неидентичных волновых поля EA и ЕB представляют два состояния А и В, соответственно. Оба векторных поля удовлетворяют волновым уравнениям
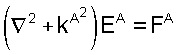
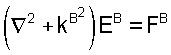
где k является волновым числом и F представляет источник объемной плотности силы. Хорошо известно, что подстановкой специальных векторов (обозначенных Q) в теорему Гаусса,
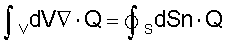
может быть получен дифферент векторной теоремы Грина. Конкретный выбор векторов в виде
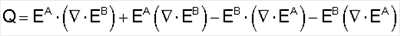
предпочтительнее для данной технологии, но могут быть также использованы другие векторы. Применив правила вычисления векторов к  ·Q и исключив симметричные члены в ЕA и ЕB, а также введя векторную идентичность ·Q и исключив симметричные члены в ЕA и ЕB, а также введя векторную идентичность  2= 2= ( ( ·)- ·)- ·( ·( ·), получим следующее выражение ·), получим следующее выражение
 ·Q=EA· ·Q=EA· 2ЕB-EB· 2ЕB-EB· 2EA 2EA
Объединив это выражение с полученным выше волновым уравнением, после подстановки в теорему Гаусса получим:
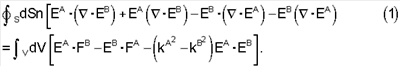
Это выражение является векторной теоремой Грина, устанавливающей взаимосвязь между двумя состояниями А и В. Каждое из этих состояний может быть связано со своими собственными характеристиками среды и своим собственным распределением источников. Первые два члена в правой части этого выражения представляют влияние возможных источников в V, которые исчезают, если в V нет никаких источников. Последние два члена в объемном интеграле представляют возможную разницу в электромагнитных свойствах среды, представленной в этих двух состояниях. Если среды идентичны, то эти два члена исчезают. Поверхностный интеграл учитывает возможную разницу во внешних граничных условиях для электромагнитных полей.
Прогнозирование диаграммы направленности излучения источника
Векторная теорема Грина используется как начальная точка для прогнозирования диаграммы излучения электромагнитного источника. Первое из двух состояний, состояние А, выбирается как физическое электромагнитное волновое поле, другое – как функция Грина однородного водного полупространства, ограниченного сверху поверхностью раздела воздух-вода. Если физические источники расположены над плоскостью, на которой были проведены измерения для первого состояния, то такой выбор состояний позволяет оценить диаграмму направленности излучения источника. Физические источники ниже плоскости (или линии) измерений не могут быть определены, но они не влияют на оценку диаграммы направленности излучения, связанную с источниками над плоскостью измерений.
При прогнозировании диаграммы направленности излучения источника для состояния А применяется геометрия, иллюстрируемая на фиг.3. Замкнутая поверхность S состоит из плоскости (Sr) 6, на которой записываются данные физических измерений, и замкнутого вверху полусферического купола (SR) 7 радиуса R, ограничивающего полусферический объем V. Поверхность 5 (S0) является границей раздела воздух-вода. Поэтому параметрами состояния А являются:
EA=E(x,  ) ) |
FA=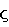 J(x, J(x,  ) ) |
HA=H(x,  ) ) |
 A= A= (x, (x,  ) ) |
JA=J(x,  ) ) |
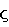 A= A=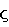 (x, (x,  ) ) |
KA=0
Эти поля удовлетворяют условиям уравнений Максвелла, которые в частотной области могут быть записаны в виде:
 ·Н(х, ·Н(х,  )- )- (x, (x,  )E(x, )E(x,  )=J(x, )=J(x,  ) )
 ·E(х, ·E(х,  )+ )+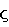 (x, (x,  )H(x, )H(x,  )=K(x, )=K(x,  ) )
Волновым уравнением для электрического поля является выражение 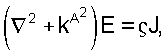 а предположение о нулевой объемной плотности означает, что а предположение о нулевой объемной плотности означает, что  ·E=0. ·E=0.
Геометрия, применявшаяся для идеализированного состояния В, иллюстрируется на фиг.4. Состояние В представляет функцию Грина однородного водного слоя в виде полупространства, ограниченного сверху границей раздела воздух-вода. Функция Грина удовлетворяет выходным граничным условиям и является причинной функцией.
Поверхности, принятые для состояния А, также выбраны и для состояния В, хотя следует отметить, что поверхность Sr в состоянии В является произвольной нефизической границей, тогда как в состоянии А она представляет морское дно. Математически требование, чтобы водный слой в виде полупространства в идеализированном состоянии был однородным (ограниченным только поверхностью воздух-вода), эквивалентно требованию выходных граничных условий на Sr для функции Грина. В интегральном представлении уравнения (1) для электромагнитного поля достаточным является рассмотрение скалярной функции Грина, хотя тензорная функция Грина также может быть использована. В самом простом способе увязки вектора ЕB со скалярной функцией Грина G принимается, что ЕB=Gc, где с является произвольным, но постоянным вектором. Функция Грина удовлетворяет дифференциальному уравнению
( 2+k2)G(х, 2+k2)G(х, ;х0)=- ;х0)=- (х-х0), (х-х0),
где x0 является координатой источника в функции Грина и учитывает влияние морской поверхности.
Пункт источника x0 функции Грина предпочтительнее располагать ниже регистрирующей плоскости Sr (т.е. вне рассматриваемого объема). Во всем объеме V параметры среды для функции Грина идентичны физическим параметрам среды. Таким образом, в состоянии В, внутри объема V соответствующими параметрами являются
EB=cG(x, ;x0) ;x0) |
FB=0 |
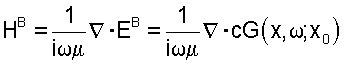 |
 B= B= (x, (x, ) ) |
| JB=0 |
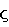 B= B=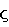 (x, (x, ) ) |
| KB=0 |
|
Эти параметры могут быть затем подставлены в векторную теорему Грина уравнения 1. Далее, радиус R полусферического купола SR может увеличиваться до бесконечности, так что SR будет приближаться к бесконечной полусферической оболочке, в этом случае ее вклад в поверхностный интеграл стремится к нулю в соответствии с условиями излучения Silver-Müller. Учитывая это, получим
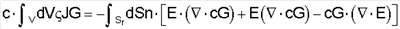
Использование идентичности векторов
n·[E·( ·Gc)]=c·[(n·E)· ·Gc)]=c·[(n·E)· G] G]
n·[E( ·cG)]=c· ·cG)]=c· G(n·E) G(n·E)
n·[cG·( ·E)]=c· ·E)]=c·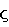 G(n·H) G(n·H)
дает затем

Поскольку с является произвольным вектором, то

Функция Грина G связывается с распространением электромагнитной волны в водном полупространстве. Интеграл по объему в левой части вышеприведенного уравнения должен поэтому представлять падающее волновое поле в x0, создаваемое электромагнитными источниками. Обозначим падающее волновое поле как Е(inc), где
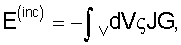
падающее волновое поле может рассматриваться как линейная комбинация вкладов от всех элементарных источников J(x, )dx. Волновое поле электромагнитного источника в любой точке x0 ниже плоскости приемников для любого неизвестного и/или распределенного источника с анизотропной диаграммой направленности излучения над плоскостью приемников может быть поэтому представлено в следующем виде )dx. Волновое поле электромагнитного источника в любой точке x0 ниже плоскости приемников для любого неизвестного и/или распределенного источника с анизотропной диаграммой направленности излучения над плоскостью приемников может быть поэтому представлено в следующем виде
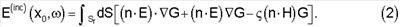
Пункты x0 могут быть выбраны в любом месте на или ниже Sr. При вычислении уравнения (2) в пунктах x0, совпадающих с положением приемников, использовавшихся для получения измеренных данных, будет получено падающее волновое поле от источника на приемниках. Вычисляя уравнение (2) для различных значений x0, например, при постоянном радиусе от известного положения источника, может быть определена относительная интенсивность диаграммы направленности излучения источника, как функция угла.
Уравнение (2) может быть записано в компонентной форме для х=(x1, х2, x3) и x0=(x10, x20, x30) в виде
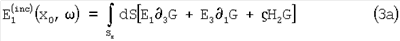
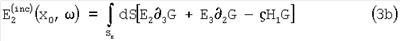
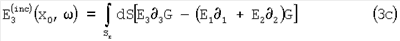
Где Еi=Еi(х1,х2,х3, ), Нi=Нi(х1,х2,х3, ), Нi=Нi(х1,х2,х3, ), Gi=Gi(x10,x20,x30, ), Gi=Gi(x10,x20,x30, ; x1,x2,x3), dS=dS(x1,x2), ; x1,x2,x3), dS=dS(x1,x2),  i= i= / / хi, и i=1, 2, 3. хi, и i=1, 2, 3.
Уравнения 2 и 3а-3с зависят исключительно от падающего электромагнитного поля. Это подтверждается тем, что левая сторона уравнений зависит только от падающего поля в полупространстве водного слоя. В правой стороне общие поля зависят как от падающего волнового поля, так и от свойств глубинных отложений в земле. Однако интеграл действует как фильтр, который удаляет все волны за исключением падающего электромагнитного волнового поля. Поэтому правая сторона также зависит только от падающего волнового поля. Поэтому измерение только одних электрических и магнитных полей является достаточным для определения диаграммы направленности излучения источника без какой-либо информации о глубинных отложениях.
Уравнение 2 зависит от нормальной компоненты электрического поля к поверхности Sr через член n·Е. Для горизонтальной записывающей плоскости n·Е=ЕЗ является вертикальной компонентной электрического поля (в предположении, что ось глубин положительна при направлении вниз). Если нормальная компонента не измерена, то решение для диаграммы направленности излучения источника может быть получено на основе тангенциальной (горизонтальной) компоненты волнового поля на Sr. Это может быть продемонстрировано путем исключения Е3 с использованием уравнений Максвелла,
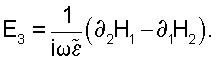
Поскольку G=G(x10-x1,x20-x2,x30, ; x3), интеграл члена с n·Е в уравнении 2 является двумерной пространственной сверткой по горизонтальным координатам, которая может быть проинтегрирована по частям, что даст ; x3), интеграл члена с n·Е в уравнении 2 является двумерной пространственной сверткой по горизонтальным координатам, которая может быть проинтегрирована по частям, что даст
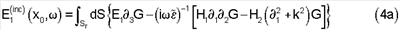
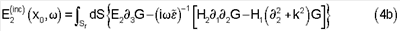
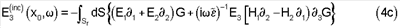
Соответствующий источник магнитных полей можно получить из уравнений 3а-3с и 4а-4с, используя соотношение Н(inc)(х0, )=- )=-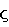 -1 -1 ·E(inc). ·E(inc).
Прогнозируемая диаграмма направленности излучения может быть использована для моделирования, обработки и дополнительной интерпретации морских электромагнитных данных. Например, определенная диаграмма направленности излучения источника может быть удалена из измеренных данных, при этом останутся только те данные, которые соответствуют области ниже плоскости приемников, т.е. морского дна, если приемники размещались на нем.
Описанные выше способы обработки данных могут быть реализованы путем программного управления компьютером, выполняющим данную технологию. Программа может храниться в запоминающих устройствах (носителях информации), например твердых или гибких дисках, CD- и DVD-воспроизводимых дисках или флеш-памяти. Программа может также передаваться через компьютерную сеть, например, Интернет или группу компьютеров, объединенных вместе в локальную сеть.
Блок-схема по фиг.5 иллюстрирует вариант способа согласно настоящему изобретению. Данные, полученные в процессе морской электромагнитной съемки, регистрируются на этапе 30 с использованием оборудования, показанного на фиг.1. На этапе 31 вычисляется функция Грина для идеализированного водного полупространства, и затем определяются ее пространственные производные (этап 32). Затем составляется поверхностный интеграл по данным, взвешенным с использованием функции Грина и ее пространственных производных, в соответствии с приведенным выше описанием, и последовательно вычисляется (этап 33) в пункте, расположенном на или ниже плоскости, на которой проводились измерения. Результатом будет диаграмма направленности излучения источника (этап 34).
Схематическая диаграмма на фиг.6 иллюстрирует центральный процессор (CPU) 13, соединенный с постоянным запоминающим устройством (ROM) 10 и оперативной памятью (RAM) 12. CPU получает данные 14 от приемников через устройство ввода-вывода 15. CPU затем определяет диаграмму направленности излучения источника 16 в соответствии с инструкциями, получаемыми из блока памяти 11 с записанной программой, который может быть частью ROM 10. Сама программа или любые входные и/или выходные данные могут быть получены или переданы через сеть 18 передачи данных, в качестве которой может быть, например, Интернет. Эта же система или отдельная система может быть использована для корректировки EM-SBL данных с целью удаления диаграммы направленности излучения источника из зарегистрированных данных, для получения модифицированных EM-SBL данных 17, которые могут дополнительно обрабатываться.
Для специалиста должна быть очевидна возможность многочисленных модификаций описанных вариантов осуществления без выхода за рамки данного изобретения, определяемые приложенной формулой.
Формула изобретения
1. Способ определения диаграммы направленности излучения источника, от, по меньшей мере, одного источника электромагнитного излучения, включающий следующие этапы:
измерение электрического и магнитного полей, создаваемых указанным, по меньшей мере, одним источником на, по меньшей мере, одном детекторе;
составление поверхностного интеграла по измеренным данным, взвешенным с использованием функции Грина и ее пространственных производных; и
вычисление поверхностного интеграла в, по меньшей мере, одном пункте для определения диаграммы направленности излучения источника в указанном пункте от указанного, по меньшей мере, одного источника.
2. Способ по п.1, отличающийся тем, что поверхностный интеграл получают с использованием векторной теоремы Грина для двух неидентичных состояний.
3. Способ по п.2, отличающийся тем, что первое состояние является реальным физическим состоянием, а второе состояние – идеализированным состоянием.
4. Способ по п.3, отличающийся тем, что реальное физическое состояние включает плоскость, содержащую, по меньшей мере, один детектор.
5. Способ по п.3 или 4, отличающийся тем, что идеализированное состояние включает полупространство, ограниченное сверху граничной поверхностью.
6. Способ по п.5, отличающийся тем, что полупространство является полубесконечным водным слоем, ограниченным сверху граничной поверхностью вода-воздух.
7. Способ по любому из пп.2-4 или 6, отличающийся тем, что оба неидентичных состояния имеют одинаковые свойства среды над плоскостью, содержащей, по меньшей мере, один детектор.
8. Способ по п.1, отличающийся тем, что функция Грина является скалярной функцией Грина.
9. Способ по п.1, отличающийся тем, что функция Грина является тензорной функцией Грина.
10. Способ по п.3, отличающийся тем, что функция Грина описывает распространение электромагнитной волны.
11. Способ по п.3, отличающийся тем, что функция Грина описывает электромагнитное рассеяние.
12. Способ по п.10 или 11, отличающийся тем, что функция Грина описывает электромагнитные волны в идеализированном состоянии.
13. Способ по п.1, отличающийся тем, что поверхностный интеграл, используемый для определения диаграммы направленности излучения источника электрического поля Е(inc), задан формулой 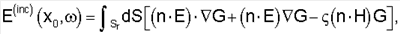
где падающее электрическое волновое поле вычисляется в пункте x0,  – угловая частота, Sr – поверхность, на которой выполняется интегрирование, n – нормальный вектор к поверхности, Е – напряженность электрического поля, Н – напряженность магнитного поля, G – функция Грина, – угловая частота, Sr – поверхность, на которой выполняется интегрирование, n – нормальный вектор к поверхности, Е – напряженность электрического поля, Н – напряженность магнитного поля, G – функция Грина,  – продольный импеданс на единицу длины среды. – продольный импеданс на единицу длины среды.
14. Способ по п.1, отличающийся тем, что поверхностный интеграл, используемый для определения диаграммы направленности излучения источника магнитного поля Н(inc), задан формулой 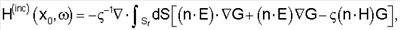
где падающее магнитное волновое поле вычисляется в пункте x0,  – угловая частота, Sr – поверхность, на которой выполняется интегрирование, n – нормальный вектор к поверхности, Е – напряженность электрического поля, Н – напряженность магнитного поля, G – функция Грина, – угловая частота, Sr – поверхность, на которой выполняется интегрирование, n – нормальный вектор к поверхности, Е – напряженность электрического поля, Н – напряженность магнитного поля, G – функция Грина,  – продольный импеданс на единицу длины среды. – продольный импеданс на единицу длины среды.
15. Способ по п.13 или 14, отличающийся тем, что величину поверхностного интеграла определяют приближенно с использованием численных методов интегрирования.
16. Способ по п.1, отличающийся тем, что поверхностный интеграл вычисляют в пункте расположения, по меньшей мере, одного детектора.
17. Способ по п.1, отличающийся тем, что поверхностный интеграл вычисляют в любом пункте ниже пункта расположения, по меньшей мере, одного детектора.
18. Способ по п.1, отличающийся тем, что поверхностный интеграл вычисляют в пунктах, расположенных на постоянном радиусе от известного пункта источника, для определения зависимости диаграммы направленности излучения источника от угла.
19. Способ по п.1, отличающийся тем, что, по меньшей мере, один детектор используют при проведении электромагнитного профилирования морского дна (EM-SBL).
20. Способ по п.1, отличающийся тем, что предусмотрена дальнейшая обработка электромагнитных данных, включающая следующие этапы:
сравнение диаграммы направленности излучения источника с электромагнитными данными, зарегистрированными, по меньшей мере, одним детектором; и
разделение диаграммы направленности излучения источника и измеренных электромагнитных данных.
21. Способ по п.20, отличающийся тем, что удаляют диаграмму направленности излучения источника.
22. Способ по п.20 или 21, отличающийся тем, что данные являются ЕМ-SBL данными, а, по меньшей мере, один детектор размещают на морском дне.
23. Способ по п.1 или 20, отличающийся тем, что для осуществления способа используют носитель информации с записанной на нем программой, непосредственно используемый в работе компьютера.
24. Способ по п.1 или 20, отличающийся тем, что для осуществления способа используют компьютер.
25. Способ по п.1, отличающийся тем, что определенную диаграмму направленности излучения источника применяют для моделирования электромагнитных данных.
26. Способ по п.1, отличающийся тем, что определенную диаграмму направленности излучения источника применяют для обработки электромагнитных данных.
27. Способ по п.1, отличающийся тем, что определенную диаграмму направленности излучения источника применяют для интерпретации электромагнитных данных.
28. Устройство для определения диаграммы направленности излучения источника от, по меньшей мере, одного источника электромагнитного излучения, содержащее, по меньшей мере, один детектор для измерения электрического и магнитного полей, создаваемых указанным, по меньшей мере, одним источником; средства для составления поверхностного интеграла по измеренным данным, взвешенным с использованием функции Грина и ее пространственных производных; и средства для вычисления поверхностного интеграла в, по меньшей мере, одном пункте для определения диаграммы направленности излучения источника в указанном пункте от указанного, по меньшей мере, одного источника.
РИСУНКИ
|
|