|
|
(21), (22) Заявка: 2007129317/09, 30.07.2007
(24) Дата начала отсчета срока действия патента:
30.07.2007
(46) Опубликовано: 10.03.2009
(56) Список документов, цитированных в отчете о
поиске:
RU 2297728 C1, 24.04.2007. RU 2298884 C2, 10.05.2007. WO 0103423 А1, П.01.2001. RU 2178626 C1, 20.01.2002. FISCHER A. Stable Scene-based Non-uniformity Correction Coefficients for Hyperspectral SWIR Sensors, Aerospace Conference, 2007 IEEE Volume, Issue, 3-10 March 2007. ROBERT A. LEATHERS et al. Scene-based nonuniformity corrections for optical and SWIR pushbroom sensors. Optical Society of America, 2005.
Адрес для переписки:
111123, Москва, ш. Энтузиастов, 46/2, ФГУП “НПО “Орион”, патентно-лицензионный отдел
|
(72) Автор(ы):
Жегалов Станислав Иванович (RU),
Соляков Владимир Николаевич (RU),
Филачев Анатолий Михайлович (RU)
(73) Патентообладатель(и):
Федеральное государственное унитарное предприятие “НПО “Орион” (RU)
|
(54) СПОСОБ КОРРЕКЦИИ НЕОДНОРОДНОСТИ МАТРИЧНЫХ ФОТОПРИЕМНЫХ УСТРОЙСТВ С МИКРОСКАНИРОВАНИЕМ
(57) Реферат:
Изобретение относится к оптико-электронным системам формирования и обработки инфракрасных изображений, для которых актуальна задача устранения неоднородности сигналов, обусловленной различиями в чувствительности к входному потоку и в темновом токе элементов фотоприемных устройств (ФПУ), с использованием только сигналов сцены. Техническим результатом является коррекция по сигналам сцены неоднородности матричных многоэлементных фотоприемных устройств для изображений с высоким пространственным разрешением, получаемых с помощью микросканирования со сдвигом падающего на матрицу фотоприемного устройства изображения сцены на полпиксела по траектории вверх-вправо-вниз-влево. Технический результат достигается тем, что регистрируют отсчеты элементов ФПУ по сигналам сцены, по отсчетам определяют корректирующие коэффициенты по смещению и чувствительности, корректируют отсчеты сцены. Для повышения точности корректирующих коэффициентов изменяют отсчеты сцены по направлениям микросканирования. 4 ил.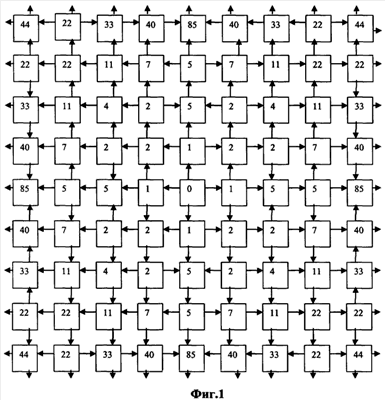
Изобретение относится к оптикоэлектронным системам формирования и обработки инфракрасных изображений, для которых актуальна задача устранения неоднородности сигналов, обусловленной различиями в чувствительности к входному потоку и в темновом токе элементов фотоприемных устройств (ФПУ), с использованием только сигналов сцены. Это дает возможность коррекции неоднородности без применения источников эталонных сигналов с их необходимостью подстройки под сцену и поддержания однородности эталонного сигнала. В некоторых случаях наличие эталонных источников неприемлемо по условиям размещения их в аппаратуре. Еще более актуальна задача коррекции неоднородности по сигналам сцены для ФПУ с микросканированием, используемым для повышения разрешающей способности тепловизионных систем.
Изобретение может использоваться в тепловизионных системах с матричными ФПУ.
Известен [1] способ выравнивания каналов тепловизионных приемников при использовании метода микросканирования (способ рассматривается в качестве аналога), заключающийся в том, что с помощью микросканирования получают два изображения одной и той же сцены, сдвинутые друг относительно друга на один элемент матрицы ФПУ. По разностным сигналам сдвинутых изображений вначале выравнивают чувствительности каналов, а затем, зная чувствительности, выравнивают значения темновых токов каналов. По этим чувствительностям и темновым токам и выравниваются принятые сигналы.
Сущность способа состоит в том, что сдвинутое на элемент матрицы изображение той же сцены обеспечивает сопоставление сигналов соседних элементов при одинаковых потоках (входных сигналах) на этих элементах. Условие одинаковых потоков позволяет оценить отношения чувствительностей соседних элементов и относительные смещения (относительные темновые токи), и через отношения соседних привести чувствительности и смещения всех элементов матрицы к чувствительности и смещению одного из элементов матрицы.
Недостаток способа вытекает из условия, что микросканирование используется только как средство для коррекции неоднородности, включая и устранение влияния неработоспособных элементов. Необходимый для этого способа сдвиг изображения на элемент матрицы не позволяет применить способ для случая сдвига изображения сцены на полпиксела (полэлемента матрицы) [2], при котором достигается увеличение пространственного разрешения вдвое. Используемой на практике траекторией сдвигов – по терминологии [2], является четырехпозиционная траектория: исходное положение, вправо на 1/2 пиксела (элемента матрицы), вниз на 1/2 пиксела, влево на 1/2 пиксела, вверх на 1/2 пиксела, т.е. в исходное положение. В [2] же приведена схема реализации такой траектории.
Наиболее близким по технической сущности к заявляемому изобретению является способ [3] коррекции неоднородности матричных ФПУ, его рассматриваем в качестве прототипа. Этот способ обеспечивает коррекцию неоднородности без учета специфики микросканирования. Добавлением в него операции по изменению сигналов ФПУ с микросканированием, по которым определяются корректирующие коэффициенты, получается заявляемый способ коррекции неоднородности для ФПУ с микросканированием, с высокой разрешающей способностью.
Сущность способа-прототипа заключается в том, что регистрируют отсчеты элементов ФПУ по сигналам сцены, по отсчетам сцены определяют корректирующие коэффициенты по чувствительности и смещению – вначале по множествам пар отсчетов сигналов соседних элементов Si(t) и Si+1(t), i N, N – множество элементов устройства, t – параметр времени, определяют отношения чувствительностей и относительные смещения соседних элементов из линейной регрессии выборки отсчетов сигналов Si(t), t=1, 2, …, T по выборке Si+1(t), t=1, 2, …, T и линейной регрессии отсчетов Si+1(t) по Si(t), N, N – множество элементов устройства, t – параметр времени, определяют отношения чувствительностей и относительные смещения соседних элементов из линейной регрессии выборки отсчетов сигналов Si(t), t=1, 2, …, T по выборке Si+1(t), t=1, 2, …, T и линейной регрессии отсчетов Si+1(t) по Si(t),
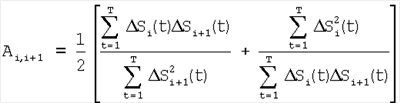
Bi,i+1=Si-Ai,i+1Si+1,
где Ai,i+1 – отношение чувствительности i-го элемента к чувствительности соседнего (i+1)-го элемента;
 Si(t)=Si(t)-Si, Si(t)=Si(t)-Si,  Si+1(t)=Si+1(t)-Si+1; Si+1(t)=Si+1(t)-Si+1;
Si и Si+1 – средние значения сигналов соседних i-го и (i+1)-го элементов, определенные на интервале Т;
Вi,i+1 – относительное смещение,
затем определяют корректирующие коэффициенты элементов матрицы по чувствительности – 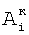 , и по смещению – , и по смещению – 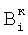 , i , i N, начиная с некоторого элемента в центре матрицы или непосредственной близости от центра, ему присваивают индекс 0 и этот элемент называют образующим 1-квадрат элементов матрицы (квадрат со стороной в 1 элемент), для «нулевого» элемента полагают N, начиная с некоторого элемента в центре матрицы или непосредственной близости от центра, ему присваивают индекс 0 и этот элемент называют образующим 1-квадрат элементов матрицы (квадрат со стороной в 1 элемент), для «нулевого» элемента полагают 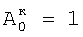 и и 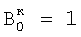 ; для каждого из четырех соседних «нулевому» элементов 3-квадрата (квадрата со стороной в 3 элемента) – их обозначают 1-элементы (см. фиг.1) по числу путей в эти элементы из «нулевого» элемента и называют следующими из «нулевого» элемента, полагают ; для каждого из четырех соседних «нулевому» элементов 3-квадрата (квадрата со стороной в 3 элемента) – их обозначают 1-элементы (см. фиг.1) по числу путей в эти элементы из «нулевого» элемента и называют следующими из «нулевого» элемента, полагают 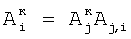 и и 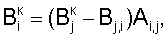 где индекс i проходит по 1-элементам, a j=0; для каждого из четырех 2-элементов (по числу путей в эти элементы из «нулевого» элемента) 3-квадрата, следующих из 1-элементов, полагают где индекс i проходит по 1-элементам, a j=0; для каждого из четырех 2-элементов (по числу путей в эти элементы из «нулевого» элемента) 3-квадрата, следующих из 1-элементов, полагают
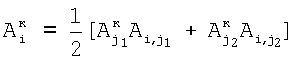 , ,
 , ,
где индекс i проходит по 2-элементам, индексы j1 и j2 соответствуют паре элементов, предшествующих i-му элементу, а номера i-x элементов, равные 2, берут равными сумме номеров предшествующих элементов; определяют корректирующие коэффициенты восьми 2-элементов периметра 5-квадрата, следующих из 2-элементов 3-квадрата: 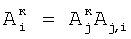 и и 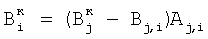 , где индекс i соответствует следующим элементам, а индекс j – предшествующим, номер 2 i-м элементам присваивают по номерам предшествующих элементов; определяют корректирующие коэффициенты 5-элементов периметра 5-квадрата, каждому из которых предшествует три элемента и каждый из которых связан с «нулевым» элементом по пяти путям, по формулам , где индекс i соответствует следующим элементам, а индекс j – предшествующим, номер 2 i-м элементам присваивают по номерам предшествующих элементов; определяют корректирующие коэффициенты 5-элементов периметра 5-квадрата, каждому из которых предшествует три элемента и каждый из которых связан с «нулевым» элементом по пяти путям, по формулам
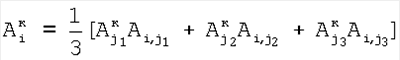 , ,
 , ,
где индекс i проходит по 5-элементам, индексы j1, j2 и j3 проходят по предшествующим элементам, номер 5 i-м элементам присваивают по сумме номеров предшествующих элементов; определяют корректирующие коэффициенты 4-элементов периметра 5-квадрата по формулам для случая двух предшествующих элементов; определяют корректирующие коэффициенты 5-элементов периметра 7-квадрата, следующие из 5-элементов периметра 5-квадрата; определяют корректирующие коэффициенты остальных элементов периметра 7-квадрата в порядке: 7-элементы, 11-элементы, 22-элементы; определяют корректирующие коэффициенты периметра 9-квадрата в порядке: 22-элементы, следующие из 22-элементов периметра 7-квадрата, 33-элементы, 40-элементы, 44-элементы, 85-элементы; по элементам периметра 9-квадрата с максимальным номером 85 определяются корректирующие коэффициенты следующих из них элементов периметра следующего, 11-квадрата, которым присваивается тот же номер; определяют корректирующие коэффициенты остальных элементов периметра 11-квадрата в порядке влево и вправо и вверх и вниз от 85-элементов; из элементов периметра 11-квадрата с максимальным номером – восьми угловых элементов, определяют следующие из этих элементов восемь элементов периметра 13-квадрата; по этим восьми элементам определяют угловые элементы 13-квадрата и по направлениям вверх-вниз и влево-вправо от этих восьми элементов определяют остальные элементы периметра 13-квадрата; определяют по элементам периметра 13-квадрата с максимальным номером – эти элементы находятся в середине сторон периметра, следующие из них элементы с таким же номером в 15-квадрате; определяют остальные элементы периметра 15-квадрата; определяют элементы с максимальным номером в 15-квадрате – они находятся в углах, определяют следующие из них элементы периметра 17-квадрата, определяют остальные элементы периметра 17-квадрата; определяют элементы 17-квадрата с максимальным номером, по ним определяют элементы с тем же номером 19-квадрата и так далее определяют элементы периметров квадратов увеличивающейся размерности, пока не будет достигнута одна или более границ матрицы, начиная откуда множество определяемых элементов наращивают только в трех или менее направлениях возможных движений от определенных к неопределенным элементам и так действуют до определения корректирующих коэффициентов всех элементов матрицы; корректируют отсчеты сигналов сцены вычитанием из значений отсчетов сцены корректирующих коэффициентов элементов по смещению и умножением разности на корректирующие коэффициенты по чувствительности,
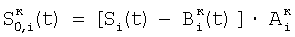 , ,
где Si(t) – корректируемый сигнал, i N, N,
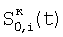 – скорректированный сигнал (относительно «нулевого» элемента). – скорректированный сигнал (относительно «нулевого» элемента).
Сущность способа-прототипа состоит в следующем.
Используя статистическую связь сигналов соседних элементов ФПУ, определяются величины Аi,i+1 – отношение чувствительностей i-го элемента к чувствительности соседнего (i+1)-го элемента и Вi,i+1 – относительное смещение этих соседних элементов для всех 2VH-(V+H) пар соседних элементов матрицы, V – высота матрицы (в элементах), Н – ширина, VH=N, соседними являются элементы, принимающие и преобразующие сигнал от смежных участков сцены – в тепловизионном изображении участку сцены соответствует пиксел кадра, смежными данному являются участки (пикселы) в направлениях «вверх-вниз» и «влево-вправо».
С увеличением интервала Т-параметра статистической обработки, относительные смещения Вi,i+1 сходятся к величинам
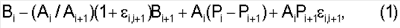
где Аi и Аi+1 – чувствительности соседних, i-го и (i+1)-го элементов, Рi и Pi+1 – средние значения потоков соответственно i-го и (i+1)-го элементов; а отношения чувствительностей Аi,i+1 сходятся к величинам

где  i,i+1 – погрешность величины Аi,i+1 относительно величины Аi/Аi+1; i,i+1 – погрешность величины Аi,i+1 относительно величины Аi/Аi+1;
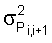 – дисперсия полусуммы потоков i-го и (i+1)-го элементов; – дисперсия полусуммы потоков i-го и (i+1)-го элементов;
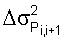 – дисперсия полуразности потоков i-го и (i+1)-го элементов; – дисперсия полуразности потоков i-го и (i+1)-го элементов;
 – дисперсия потока, эквивалентного шуму i-го элемента; – дисперсия потока, эквивалентного шуму i-го элемента;
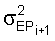 – дисперсия потока, эквивалентного шуму i+1-го элемента; – дисперсия потока, эквивалентного шуму i+1-го элемента;
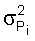 и и 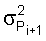 – дисперсии потоков соответственно i-го и (i-1)-го элементов. – дисперсии потоков соответственно i-го и (i-1)-го элементов.
Определяющей погрешность величин Ai,i+1 и Bi,i+1 является величина
 i,i+1 – чем ближе она к нулю, тем меньше погрешность. Относительная погрешность корректирующих коэффициентов i,i+1 – чем ближе она к нулю, тем меньше погрешность. Относительная погрешность корректирующих коэффициентов 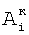 и и 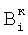 , определяемая погрешностью величин Ai,i+1 и Bi,i+1, оценивается в 2 , определяемая погрешностью величин Ai,i+1 и Bi,i+1, оценивается в 2 , где , где  – средняя по множеству погрешностей – средняя по множеству погрешностей  i,i+1 величина, а оценка относительной погрешности скорректированных значений сцены – погрешность метода – оценивается в i,i+1 величина, а оценка относительной погрешности скорректированных значений сцены – погрешность метода – оценивается в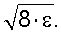
Увеличение погрешности корректирующих коэффициентов 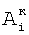 и и 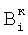 элементов ФПУ относительно элементов ФПУ относительно  только в два раза обеспечивается тем, что при их определении происходит усреднение значений этих коэффициентов по всем путям, ведущим из «нулевого» элемента в остальные элементы ФПУ. И хотя разные пути, ведущие из «нулевого» элемента в некоторый другой элемент ФПУ, содержат и общие элементы, что работает на увеличение погрешности, однако фактор снижения погрешности из-за экспоненциального роста числа путей, с удалением от «нулевого» элемента, не уступает фактору увеличения. Увеличение погрешности метода до величины только в два раза обеспечивается тем, что при их определении происходит усреднение значений этих коэффициентов по всем путям, ведущим из «нулевого» элемента в остальные элементы ФПУ. И хотя разные пути, ведущие из «нулевого» элемента в некоторый другой элемент ФПУ, содержат и общие элементы, что работает на увеличение погрешности, однако фактор снижения погрешности из-за экспоненциального роста числа путей, с удалением от «нулевого» элемента, не уступает фактору увеличения. Увеличение погрешности метода до величины 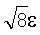 , с величины погрешности корректирующих коэффициентов в 2 , с величины погрешности корректирующих коэффициентов в 2 , определяется процедурой корректирования, состоящей в умножении нескорректированного значения сигнала на корректирующий коэффициент по чувствительности и добавлении к результату корректирующего коэффициента по смещению. , определяется процедурой корректирования, состоящей в умножении нескорректированного значения сигнала на корректирующий коэффициент по чувствительности и добавлении к результату корректирующего коэффициента по смещению.
В известном способе-прототипе, по мнению авторов предлагаемого изобретения, лежащие в основе погрешности метода величины  i,i+1 зависят от соотношения потоков на соседних элементах и, как следует из формулы (2), при стремлении потоков соседних элементов к равенству в среднем – равенству их средних отклонений и равенству средних значений потоков и соответственно стремящейся при этом к нулю дисперсии полуразности этих потоков, будут уменьшаться и зависеть только от отношения «шум элементов/поток элементов» – i,i+1 зависят от соотношения потоков на соседних элементах и, как следует из формулы (2), при стремлении потоков соседних элементов к равенству в среднем – равенству их средних отклонений и равенству средних значений потоков и соответственно стремящейся при этом к нулю дисперсии полуразности этих потоков, будут уменьшаться и зависеть только от отношения «шум элементов/поток элементов» – 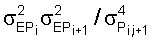 . Практические величины отношения отклонения ошибки к потоку – порядка 0.2 и меньше дают отношение «шум элементов/поток элементов» порядка 1/625 и меньше. Это соответствует ошибке метода около 1%. Погрешность определения Вi,i+1 стремит к нулю равенство средних значений потоков, при этом величина (1) стремится к Вi-(Аi/Аi+1)Вi+1 – точному соотношению смещений соседних элементов. . Практические величины отношения отклонения ошибки к потоку – порядка 0.2 и меньше дают отношение «шум элементов/поток элементов» порядка 1/625 и меньше. Это соответствует ошибке метода около 1%. Погрешность определения Вi,i+1 стремит к нулю равенство средних значений потоков, при этом величина (1) стремится к Вi-(Аi/Аi+1)Вi+1 – точному соотношению смещений соседних элементов.
Равенство в среднем потоков соседних элементов достигается тем, что соседние элементы регистрируют соседние элементы сцены, которые сильно коррелированы, и корреляция растет с увеличением интервала Т. Соответственно, с ростом Т увеличивается и точность метода коррекции.
Уменьшить интервал Т, на котором определяются коэффициенты коррекции, и с удовлетворительной точностью – такую возможность дает микросканирование посредством сдвига попадающего на элементы ФПУ сигнала сцены относительно этих элементов и его фиксации для разных направлений сдвига. Сравнением сигналов соседних элементов по вертикали и горизонтали с определенным выбором фаз и модификацией сигналов осуществляется сопоставление сигналов соседних элементов с соизмеримыми потоками.
В известном способе коррекции неоднородности матричных ФПУ не достигается уменьшение интервала Т, возможность которого обеспечивает микросканирование.
Целью настоящего изобретения является коррекция по сигналам сцены неоднородности матричных многоэлементных фотоприемных устройств для изображений с высоким пространственным разрешением, получаемых с помощью микросканирования со сдвигом падающего на матрицу фотоприемного устройства изображения сцены на полпиксела по траектории вверх-вправо-вниз-влево.
Технический результат достигается тем, что регистрируют отсчеты элементов ФПУ по сигналам сцены, по отсчетам сцены определяют корректирующие коэффициенты по чувствительности и смещению – вначале по множествам пар отсчетов сигналов соседних элементов Si(t) и Si+1(t), i N, N – множество элементов устройства, t – параметр времени, определяют отношения чувствительностей и относительные смещения соседних элементов из линейной регрессии выборки отсчетов сигналов Si(t), t=1, 2, …, T по выборке Si+1(t), t=1, 2, …, T и линейной регрессии отсчетов Si+1(t) по Si(t), причем для соседних в матрице элементов по вертикали в качестве Si(t) берут отсчеты N, N – множество элементов устройства, t – параметр времени, определяют отношения чувствительностей и относительные смещения соседних элементов из линейной регрессии выборки отсчетов сигналов Si(t), t=1, 2, …, T по выборке Si+1(t), t=1, 2, …, T и линейной регрессии отсчетов Si+1(t) по Si(t), причем для соседних в матрице элементов по вертикали в качестве Si(t) берут отсчеты 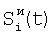 , которые получают по формуле , которые получают по формуле 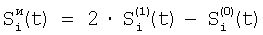 , и в качестве Si+1(t) берут , и в качестве Si+1(t) берут 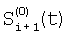 , для соседних в матрице элементов по горизонтали в качестве Si(t) берут отсчеты , для соседних в матрице элементов по горизонтали в качестве Si(t) берут отсчеты 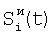 , которые получают по формуле , которые получают по формуле 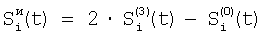 , и в качестве Si+1(t) берут , и в качестве Si+1(t) берут 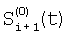 , где величины , где величины 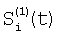 и и 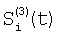 – отсчеты ФПУ с микросканированием со сдвигом изображения сцены на полэлемента матрицы вверх – отсчеты – отсчеты ФПУ с микросканированием со сдвигом изображения сцены на полэлемента матрицы вверх – отсчеты 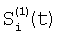 и на полэлемента вправо – отсчеты и на полэлемента вправо – отсчеты 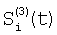 , относительно некоторого положения изображения – отсчеты , относительно некоторого положения изображения – отсчеты 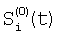 , ,
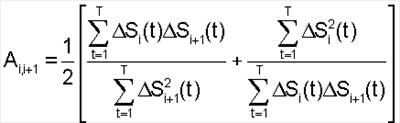
Bi,i+1=Si-Ai,i+1Si+1,
где Аi,i+1 – отношение чувствительности i-го элемента к чувствительности соседнего (i+1)-го элемента;
 Si(t)=Si(t)-Si, Si(t)=Si(t)-Si,  Si+1(t)=Si+1(t)-Si+1; Si+1(t)=Si+1(t)-Si+1;
Si и Si+1 – средние значения сигналов соседних i-го и (i+1)-го элементов, определенные на интервале Т;
Вi,i+1 – относительное смещение,
затем определяют корректирующие коэффициенты элементов матрицы по чувствительности – 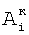 и по смещению – и по смещению – 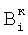 , i , i N, начиная с некоторого элемента в центре матрицы или непосредственной близости от центра – ему присваивают индекс 0, и этот элемент называют образующим 1-квадрат элементов матрицы (квадрат со стороной в 1 элемент), для «нулевого» элемента полагают N, начиная с некоторого элемента в центре матрицы или непосредственной близости от центра – ему присваивают индекс 0, и этот элемент называют образующим 1-квадрат элементов матрицы (квадрат со стороной в 1 элемент), для «нулевого» элемента полагают 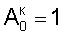 и и 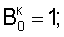 для каждого из четырех соседних «нулевому» элементов 3-квадрата (квадрата со стороной в 3 элемента) – их обозначают 1-элементы (см. фиг.1) по числу путей в эти элементы из «нулевого» элемента и называют следующими из «нулевого» элемента, полагают для каждого из четырех соседних «нулевому» элементов 3-квадрата (квадрата со стороной в 3 элемента) – их обозначают 1-элементы (см. фиг.1) по числу путей в эти элементы из «нулевого» элемента и называют следующими из «нулевого» элемента, полагают 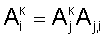 и и 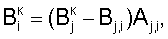 где индекс i проходит по 1-элементам, a j=0; для каждого из четырех 2-элементов (по числу путей в эти элементы из «нулевого» элемента) 3-квадрата, следующих из 1-элементов, полагают где индекс i проходит по 1-элементам, a j=0; для каждого из четырех 2-элементов (по числу путей в эти элементы из «нулевого» элемента) 3-квадрата, следующих из 1-элементов, полагают
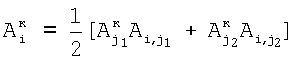 , ,
 , ,
где индекс i проходит по 2-элементам, индексы j1 и j2 соответствуют паре элементов, предшествующих i-му элементу, а номера i-x элементов, равные 2, берут равными сумме номеров предшествующих элементов; определяют корректирующие коэффициенты восьми 2-элементов периметра 5-квадрата, следующих из 2-элементов 3-квадрата: 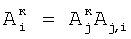 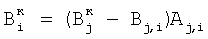 и, где индекс i соответствует следующим элементам, а индекс j – предшествующим, номер 2 i-м элементам присваивают по номерам предшествующих элементов; определяют корректирующие коэффициенты 5-элементов периметра 5-квадрата, каждому из которых предшествует три элемента и каждый из которых связан с «нулевым» элементом по пяти путям, по формулам и, где индекс i соответствует следующим элементам, а индекс j – предшествующим, номер 2 i-м элементам присваивают по номерам предшествующих элементов; определяют корректирующие коэффициенты 5-элементов периметра 5-квадрата, каждому из которых предшествует три элемента и каждый из которых связан с «нулевым» элементом по пяти путям, по формулам
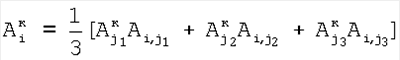 , ,
 , ,
где индекс i проходит по 5-элементам, индексы j1, j2 и j3 проходят по предшествующим элементам, номер 5 i-м элементам присваивают по сумме номеров предшествующих элементов; определяют корректирующие коэффициенты 4-элементов периметра 5-квадрата по формулам для случая двух предшествующих элементов; определяют корректирующие коэффициенты 5-элементов периметра 7-квадрата, следующие из 5-элементов периметра 5-квадрата; определяют корректирующие коэффициенты остальных элементов периметра 7-квадрата в порядке: 7-элементы, 11-элементы, 22-элементы; определяют корректирующие коэффициенты периметра 9-квадрата в порядке: 22-элементы, следующие из 22-элементов периметра 7-квадрата, 33-элементы, 40-элементы, 44-элементы, 85-элементы; по элементам периметра 9-квадрата с максимальным номером 85 определяются корректирующие коэффициенты следующих из них элементов периметра следующего, 11-квадрата, которым присваивается тот же номер; определяют корректирующие коэффициенты остальных элементов периметра 11-квадрата в порядке влево и вправо и вверх и вниз от 85-элементов; из элементов периметра 11-квадрата с максимальным номером – восьми угловых элементов определяют следующие из этих элементов восемь элементов периметра 13-квадрата; по этим восьми элементам определяют угловые элементы 13-квадрата и по направлениям вверх-вниз и влево-вправо от этих восьми элементов определяют остальные элементы периметра 13-квадрата; определяют по элементам периметра 13-квадрата с максимальным номером – эти элементы находятся в середине сторон периметра, следующие из них элементы с таким же номером в 15-квадрате; определяют остальные элементы периметра 15-квадрата; определяют элементы с максимальным номером в 15-квадрате – они находятся в углах, определяют следующие из них элементы периметра 17-квадрата, определяют остальные элементы периметра 17-квадрата; определяют элементы 17-квадрата с максимальным номером, по ним определяют элементы с тем же номером 19-квадрата и так далее определяют элементы периметров квадратов увеличивающейся размерности, пока не будет достигнута одна или более границ матрицы, начиная откуда множество определяемых элементов наращивают только в трех или менее направлениях возможных движений от определенных к неопределенным элементам и так действуют до определения корректирующих коэффициентов всех элементов матрицы: корректируют отсчеты сигналов сцены вычитанием из значений отсчетов сцены корректирующих коэффициентов элементов по смещению и умножением разности на корректирующие коэффициенты по чувствительности,
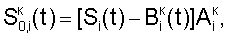
где Si(t) – корректируемый сигнал, i N, N,
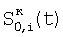 – скорректированный сигнал (относительно «нулевого» элемента). – скорректированный сигнал (относительно «нулевого» элемента).
Предлагаемое изобретение поясняется следующими чертежами, где:
фиг.1. Схема обхода элементов матрицы ФПУ (относится и к прототипу);
фиг.2. Фазы сдвига сцены относительно элемента (пиксела) матрицы при микросканировании на половину пиксела;
фиг.3. Соотношение потоков сцены и элементов некоторого (любого) столбца матрицы соответственно для фаз 0 и 1;
фиг.4. Схема устройства, реализующего предлагаемый способ.
Сущность заявляемого способа состоит в следующем.
Способ регистрируют отсчеты элементов ФПУ по сигналам сцены, по отсчетам сцены определяют корректирующие коэффициенты по чувствительности и смещению – вначале по множествам пар отсчетов сигналов соседних элементов Si(t) и Si+1(t), i N, N – множество элементов устройства, t – параметр времени, определяют отношения чувствительностей и относительные смещения соседних элементов из линейной регрессии выборки отсчетов сигналов Si(t), t=1, 2, …, T по выборке Si+1(t), t=1, 2, …,T и линейной регрессии отсчетов Si+1(t) по Si(t), причем для соседних в матрице элементов по вертикали в качестве Si(t) берут отсчеты N, N – множество элементов устройства, t – параметр времени, определяют отношения чувствительностей и относительные смещения соседних элементов из линейной регрессии выборки отсчетов сигналов Si(t), t=1, 2, …, T по выборке Si+1(t), t=1, 2, …,T и линейной регрессии отсчетов Si+1(t) по Si(t), причем для соседних в матрице элементов по вертикали в качестве Si(t) берут отсчеты 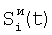 , которые получают по формуле , которые получают по формуле 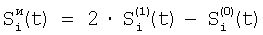 , и в качестве Si+1(t) берут , и в качестве Si+1(t) берут 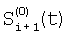 , для соседних в матрице элементов по горизонтали в качестве Si(t) берут отсчеты , для соседних в матрице элементов по горизонтали в качестве Si(t) берут отсчеты 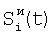 , которые получают по формуле , которые получают по формуле 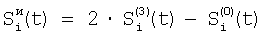 , и в качестве Si+1(t) берут , и в качестве Si+1(t) берут 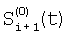 , где величины , где величины 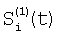 и и 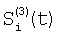 – отсчеты ФПУ с микросканированием со сдвигом изображения сцены на полэлемента матрицы вверх – отсчеты – отсчеты ФПУ с микросканированием со сдвигом изображения сцены на полэлемента матрицы вверх – отсчеты 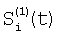 и на полэлемента вправо – отсчеты и на полэлемента вправо – отсчеты 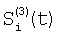 , относительно некоторого положения изображения – отсчеты , относительно некоторого положения изображения – отсчеты 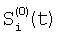 , ,
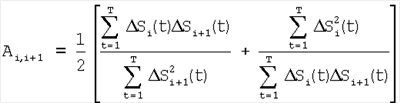
Bi,i+1=Si-Ai,i+1+Si+1,
где Ai,i+1 – отношение чувствительности i-го элемента к чувствительности соседнего (i+1)-го элемента;
 Si(t)=Si(t)-Si, Si(t)=Si(t)-Si,  Si+1(t)=Si+1(t)-Si+1; Si+1(t)=Si+1(t)-Si+1;
Si и Si+1 – средние значения сигналов соседних i-го и (i+1)-го элементов, определенные на интервале Т;
Вi,i+1 – относительное смещение,
затем определяют корректирующие коэффициенты элементов матрицы по чувствительности – 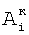 и по смещению – и по смещению – 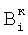 , i , i N, начиная с некоторого элемента в центре матрицы или непосредственной близости от центра, ему присваивают индекс 0 и этот элемент называют образующим 1-квадрат элементов матрицы (квадрат со стороной в 1 элемент), для «нулевого» элемента полагают N, начиная с некоторого элемента в центре матрицы или непосредственной близости от центра, ему присваивают индекс 0 и этот элемент называют образующим 1-квадрат элементов матрицы (квадрат со стороной в 1 элемент), для «нулевого» элемента полагают 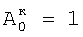 и и 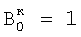 ; для каждого из четырех соседних «нулевому» элементов 3-квадрата (квадрата со стороной в 3 элемента) – их обозначают 1-элементы (см. фиг.1) по числу путей в эти элементы из «нулевого» элемента и называют следующими из «нулевого» элемента, полагают ; для каждого из четырех соседних «нулевому» элементов 3-квадрата (квадрата со стороной в 3 элемента) – их обозначают 1-элементы (см. фиг.1) по числу путей в эти элементы из «нулевого» элемента и называют следующими из «нулевого» элемента, полагают 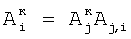 и и 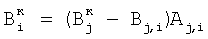 , где индекс i проходит по 1-элементам, a j=0; для каждого из четырех 2-элементов (по числу путей в эти элементы из «нулевого» элемента) 3-квадрата, следующих из 1-элементов, полагают , где индекс i проходит по 1-элементам, a j=0; для каждого из четырех 2-элементов (по числу путей в эти элементы из «нулевого» элемента) 3-квадрата, следующих из 1-элементов, полагают
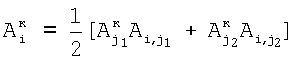 , ,
 , ,
где индекс i проходит по 2-элементам, индексы j1 и j2 соответствуют паре элементов, предшествующих i-му элементу, а номера i-x элементов, равные 2, берут равными сумме номеров предшествующих элементов; определяют корректирующие коэффициенты восьми 2-элементов периметра 5-квадрата, следующих из 2-элементов 3-квадрата: 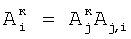 и и 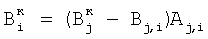 , где индекс i соответствует следующим элементам, а индекс j – предшествующим, номер 2 i-м элементам присваивают по номерам предшествующих элементов; определяют корректирующие коэффициенты 5-элементов периметра 5-квадрата, каждому из которых предшествует три элемента и каждый из которых связан с «нулевым» элементом по пяти путям, по формулам , где индекс i соответствует следующим элементам, а индекс j – предшествующим, номер 2 i-м элементам присваивают по номерам предшествующих элементов; определяют корректирующие коэффициенты 5-элементов периметра 5-квадрата, каждому из которых предшествует три элемента и каждый из которых связан с «нулевым» элементом по пяти путям, по формулам
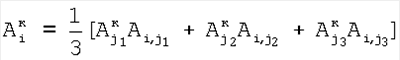 , ,
 , ,
где индекс i проходит по 5-элементам, индексы j1, j2 и j3 проходят по предшествующим элементам, номер 5 i-м элементам присваивают по сумме номеров предшествующих элементов; определяют корректирующие коэффициенты 4-элементов периметра 5-квадрата по формулам для случая двух предшествующих элементов; определяют корректирующие коэффициенты 5-элементов периметра 7-квадрата, следующие из 5-элементов периметра 5-квадрата; определяют корректирующие коэффициенты остальных элементов периметра 7-квадрата в порядке: 7-элементы, 11-элементы, 22-элементы; определяют корректирующие коэффициенты периметра 9-квадрата в порядке: 22-элементы, следующие из 22-элементов периметра 7-квадрата, 33-элементы, 40-элементы, 44-элементы, 85-элементы; по элементам периметра 9-квадрата с максимальным номером 85 определяются корректирующие коэффициенты следующих из них элементов периметра следующего, 11-квадрата, которым присваивается тот же номер; определяют корректирующие коэффициенты остальных элементов периметра 11-квадрата в порядке влево и вправо и вверх и вниз от 85-элементов; из элементов периметра 11-квадрата с максимальным номером – восьми угловых элементов определяют следующие из этих элементов восемь элементов периметра 13-квадрата; по этим восьми элементам определяют угловые элементы 13-квадрата и по направлениям вверх-вниз и влево-вправо от этих восьми элементов определяют остальные элементы периметра 13-квадрата; определяют по элементам периметра 13-квадрата с максимальным номером – эти элементы находятся в середине сторон периметра, следующие из них элементы с таким же номером в 15-квадрате; определяют остальные элементы периметра 15-квадрата; определяют элементы с максимальным номером в 15-квадрате – они находятся в углах, определяют следующие из них элементы периметра 17-квадрата, определяют остальные элементы периметра 17-квадрата; определяют элементы 17-квадрата с максимальным номером, по ним определяют элементы с тем же номером 19-квадрата и так далее определяют элементы периметров квадратов увеличивающейся размерности, пока не будет достигнута одна или более границ матрицы, начиная откуда множество определяемых элементов наращивают только в трех или менее направлениях возможных движений от определенных к неопределенным элементам и так действуют до определения корректирующих коэффициентов всех элементов матрицы; корректируют отсчеты сигналов сцены вычитанием из значений отсчетов сцены корректирующих коэффициентов элементов по смещению и умножением разности на корректирующие коэффициенты по чувствительности,
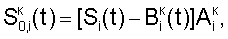
где Si(t) – корректируемый сигнал, i  N, N,
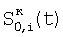 – скорректированный сигнал (относительно «нулевого» элемента). – скорректированный сигнал (относительно «нулевого» элемента).
На фиг.2 приведены фазы сдвига сцены относительно элемента (пиксела) матрицы при микросканировании на половину пиксела. Жирным обозначено положение элемента матрицы, тонким – сканирование сцены – изменение положения участка сцены размером в пиксел относительно элемента матрицы. На фиг.2 обозначены:
1 – фаза 1: сдвиг на полпиксела вверх;
2 – фаза 2: сдвиг на полпиксела вверх-вправо;
3 – фаза 3: сдвиг на полпиксела вправо;
4 – фаза 0: исходное положение;
5 – фаза 1: сдвиг на полпиксела вверх.
Фазы 0 и 1 показывают, что на рассматриваемый элемент матрицы и вышерасположенный элемент попадают частично одни и те же участки сцены – половина участка сцены, попавшего в фазе 0 на рассматриваемый элемент, в фазе 1 попадает на соседний элемент, и этот факт может быть использован для уточнения сопоставления потоков этих элементов. Подобно – фазы 0 и 3 показывают, что на рассматриваемый и соседний по горизонтали элемент попадают частично одни и те же участки сцены. Понятие «один и тот же участок сцены» подразумевает, что и состояние этого участка – его поток, остается на интервале сопоставления фаз неизменным или мало меняющимся. Практическое значения интервала между сменами фаз – 1/100 сек дает предпосылку считать поток практически неизменным. Усиливает эту предпосылку и превращает ее в основание неизменности потока статистический подход – неизменность потока рассматривается не для отдельного сопоставления фаз, а для множества таких сопоставлений.
Фиг.3 показывает соотношение потоков сцены и элементов некоторого (любого) столбца матрицы соответственно для фаз 0 и 1.
На фиг.3:
1 – столбец элементов ФПУ;
2 – сцена для фазы 0;
3 – сцена для фазы 1;
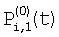 и и 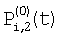 – потоки, попадающие на верхние и нижние части i-го элемента столбца для фазы 0; – потоки, попадающие на верхние и нижние части i-го элемента столбца для фазы 0;
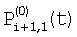 и и 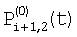 – потоки для фазы 0, попадающие на верхние и нижние части элемента i+1; – потоки для фазы 0, попадающие на верхние и нижние части элемента i+1;
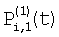 и и 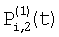 – потоки для фазы 1, попадающие на верхние и нижние части элемента i, для них можно записать: – потоки для фазы 1, попадающие на верхние и нижние части элемента i, для них можно записать:
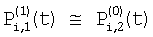 , , 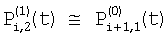 ; ;
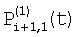 и и 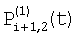 – потоки, попадающие на верхние и нижние части элемента i+1 при фазе 1, и можно записать – потоки, попадающие на верхние и нижние части элемента i+1 при фазе 1, и можно записать
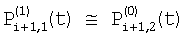 , , 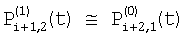 ; ;
Знак  (приблизительно равно) отражает тот факт, что строгого совпадения нет, хотя это потоки для одного и того же участка сцены, но разнесенные – пусть и на малый промежуток, во времени. (приблизительно равно) отражает тот факт, что строгого совпадения нет, хотя это потоки для одного и того же участка сцены, но разнесенные – пусть и на малый промежуток, во времени.
Совпадение потоков на соседних элементах, – по нижней части i-го элемента при фазе 0 и верхней части (i+1)-го элемента для фазы 1, потоки от одних и тех же участков сцены, – назовем совпадением по участкам сцены. Потоки на других частях соседних элементов совпадают на уровне близости соседних участков сцены.
Условия точного сопоставления – равенства потоков соседних элементов в среднем достигается в общем случае и без совпадения по участкам сцены – на большом интервале Т, за счет усреднения статистика соседних участков сближается, и чем ближе участки, тем быстрее она сближается. Т.е. разные, но близкие участки сцены, накрывающие соседние элементы, с увеличением интервала Т будут иметь совпадающие статистики – средние значения и средние отклонения, значит, и статистики соседних элементов будут сближаться. Максимальный же темп сближения будет при совпадении всех участков сцены, накрывающих соседние элементы. Для этого изменяют сигналы элементов нулевой фазы 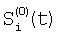 на на 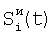 , где , где
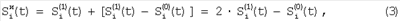
где, в свою очередь,
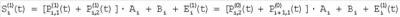 – сигнал с i-го элемента при фазе 1; – сигнал с i-го элемента при фазе 1;
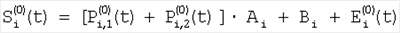 – сигнал с i-го элемента при фазе 0; – сигнал с i-го элемента при фазе 0;
Аi – чувствительность i-го элемента;
Вi – смещение i-го элемента;
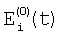 , , 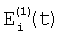 – шум при фазе 0 и 1 соответственно. – шум при фазе 0 и 1 соответственно.
Правило изменения, направленное на уравнивание потоковых составляющих в сравниваемых сигналах соседних элементов, основывается на том, что градиент потоков на соседних элементах ввиду его малости достаточно точно аппроксимируется линейной зависимостью. В результате потоковые составляющие в сигналах 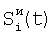 и и 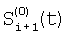 становятся сопоставимыми, что несложно проверяется подстановкой в эти сигналы линейно связанной по величине последовательности потоков для соседних участков сцены, например, такой: становятся сопоставимыми, что несложно проверяется подстановкой в эти сигналы линейно связанной по величине последовательности потоков для соседних участков сцены, например, такой: 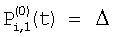 , , 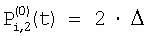 , , 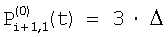 , , 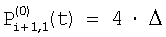 . .
Аналогично изменению сигнала (3), с целью уравнивания потоков соседних по горизонтали элементов матрицы изменяют сигналы элементов нулевой фазы 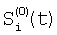 на на 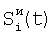 по правилу по правилу
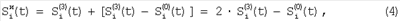
где 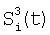 – сигнал при фазе 3. – сигнал при фазе 3.
Сформулируем правило изменения сигналов перед сопоставлением, переходя к обозначению элементов к двумерной (матричной) индексации: если через 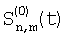 , , 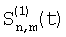 , , 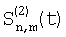 , , 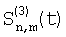 обозначим сигналы элемента матрицы соответственно фазам 0, 1, 2, 3 (каждому значению параметра t соответствуют 4 отсчета), то измененные сигналы, для сопоставлений по вертикали и горизонтали, соответственно запишутся обозначим сигналы элемента матрицы соответственно фазам 0, 1, 2, 3 (каждому значению параметра t соответствуют 4 отсчета), то измененные сигналы, для сопоставлений по вертикали и горизонтали, соответственно запишутся
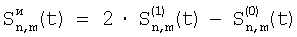 , , 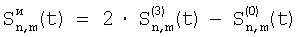 . .
Для одномерной индексации правило изменения имеет вид:
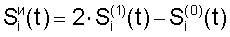 – при сопоставлении элементов по вертикали, – при сопоставлении элементов по вертикали,
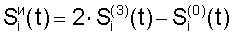 – при сопоставлении элементов по горизонтали. – при сопоставлении элементов по горизонтали.
Сопоставление элементов производят по сигналам:
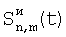 и и 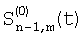 – двумерная индексация, сопоставление по вертикали; – двумерная индексация, сопоставление по вертикали;
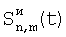 и и 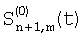 – двумерная индексация, сопоставление по горизонтали. – двумерная индексация, сопоставление по горизонтали.
Для одномерной индексации сопоставление записывается в виде 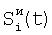 и и 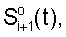 где в случае сопоставления по вертикали в качестве где в случае сопоставления по вертикали в качестве 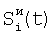 используется результат применения формулы (3), а по горизонтали – формулы (4). используется результат применения формулы (3), а по горизонтали – формулы (4).
Используя статистическую связь сигналов соседних элементов ФПУ, определяются величины Аi,i+1 – отношение чувствительностей i-го элемента к чувствительности соседнего (i+1)-го элемента и Вi,i+1 – относительное смещение соседних элементов для всех пар соседних элементов матрицы. Микросканирование и правила (3) и (4) изменения значений выборок обеспечивают точное сопоставление по потокам сигналов соседних элементов матрицы. Тем самым достигается точность определения отношений чувствительности и относительных смещений соседних элементов.
Отличие заявляемого способа от прототипа состоит в том, что на этапе определения относительных характеристик соседних элементов по выборкам Si(t) и Si+1(t), i N, N – множество элементов устройства, t – параметр времени, когда определяют отношения чувствительностей и относительные смещения соседних элементов из линейной регрессии выборки отсчетов сигналов Si(t), t=1, 2, …, T по выборке Si+1(t), t=1, 2, …, T и линейной регрессии отсчетов Si+1(t) по Si(t), для соседних в матрице элементов по вертикали в качестве Si(t) берут измененные отсчеты N, N – множество элементов устройства, t – параметр времени, когда определяют отношения чувствительностей и относительные смещения соседних элементов из линейной регрессии выборки отсчетов сигналов Si(t), t=1, 2, …, T по выборке Si+1(t), t=1, 2, …, T и линейной регрессии отсчетов Si+1(t) по Si(t), для соседних в матрице элементов по вертикали в качестве Si(t) берут измененные отсчеты 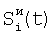 , которые получают по формуле , которые получают по формуле 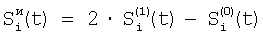 , и в качестве Si+1(t) берут , и в качестве Si+1(t) берут 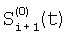 , а для соседних в матрице элементов по горизонтали в качестве Si(t) берут отсчеты , а для соседних в матрице элементов по горизонтали в качестве Si(t) берут отсчеты 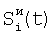 , которые получают по формуле , которые получают по формуле 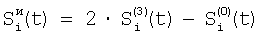 , и в качестве Si+1(t) берут , и в качестве Si+1(t) берут 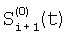 , где величины , где величины 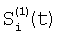 и и 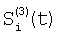 – отсчеты ФПУ с микросканированием со сдвигом изображения сцены на полэлемента матрицы вверх – отсчеты – отсчеты ФПУ с микросканированием со сдвигом изображения сцены на полэлемента матрицы вверх – отсчеты 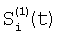 и на полэлемента вправо – отсчеты и на полэлемента вправо – отсчеты 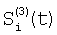 , относительно некоторого положения изображения – отсчеты , относительно некоторого положения изображения – отсчеты 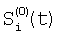 . .
Изменение выборок обеспечивает равенство потоков соседних элементов в среднем – равенство их средних отклонений и равенство средних значений потоков и соответственно приближение к нулю дисперсии полуразности этих потоков, тем самым погрешность определения отношений чувствительностей соседних элементов будет зависеть только от отношения «шум элементов/поток элементов» – 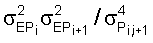 . Практические величины этого отношения составляют порядка 1/625 и меньше, что соответствует ошибке метода около 1%. Погрешность определения Вi,i+1 стремится к нулю из-за равенства средних значений потоков. . Практические величины этого отношения составляют порядка 1/625 и меньше, что соответствует ошибке метода около 1%. Погрешность определения Вi,i+1 стремится к нулю из-за равенства средних значений потоков.
На фиг.4 приведена схема устройства, реализующего предлагаемый способ.
На схеме обозначены:
1 – сигнал сцены;
2 – микросканер;
3 – матричное фотоприемное устройство;
4 – аналого-цифровой преобразователь сигналов;
5 – определитель корректирующих коэффициентов;
6 – корректор сигналов сцены;
7 – скорректированный сигнал;
8 – оптический элемент.
Микросканер обеспечивает сдвиги сигнала сцены на полпиксела относительно матрицы по четырехпозиционной траектории [2].
Определитель корректирующих коэффициентов определяет отношения чувствительностей и относительные смещения соседних элементов матрицы, по которым затем формируются корректирующие коэффициенты.
Корректор сигналов сцены с помощью корректирующих коэффициентов формирует скорректированные сигналы.
Источники
1. Статья в журнале: В.И. Соловьев, И.Ю. Анисимов. «Оценка качества выравнивания каналов тепловизионных приемников при использовании метода микросканирования». Оптический журнал, том 72, №6, 2005.
2. Статья в журнале: В.В.Тарасов, Ю.Г.Якушенков. «Некоторые пути совершенствования тепловизионных систем». Специальная техника, №2, 2004.
3. RU 2298884 C2, кл. H04N 5/33. Способ коррекции неоднородности матричных фотоприемных устройств.
Формула изобретения
Способ коррекции неоднородности матричных фотоприемных устройств с микросканированием, заключающийся в том, что регистрируют отсчеты элементов фотоприемного устройства по сигналам сцены, корректируют отсчеты сигналов сцены вычитанием из значений отсчетов сигналов сцены корректирующих коэффициентов элементов по смещению и умножением разности на корректирующие коэффициенты по чувствительности, для проведения коррекции определяют корректирующие коэффициенты элементов по чувствительности и смещению по отсчетам сцены – вначале по множествам пар отсчетов сигналов соседних элементов Si(t) и Si+1(t), i N, N – множество элементов устройства, t-параметр времени, определяют отношения чувствительностей и относительные смещения соседних элементов из линейной регрессии выборки отсчетов сигналов Si(t), t=1, 2, …, Т по выборке Si+1(t), t=1, 2, …, Т и линейной регрессии отсчетов Si+1(t) no Si(t), N, N – множество элементов устройства, t-параметр времени, определяют отношения чувствительностей и относительные смещения соседних элементов из линейной регрессии выборки отсчетов сигналов Si(t), t=1, 2, …, Т по выборке Si+1(t), t=1, 2, …, Т и линейной регрессии отсчетов Si+1(t) no Si(t),
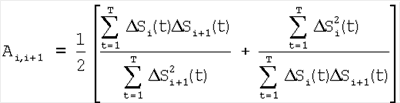 , ,
Bi,i+1=Si-Ai,i+1Si+1,
где Аi,i+1 – отношение чувствительности i-го элемента к чувствительности соседнего (i+1)-го элемента;
 Si(t)=Si(t)-Si, Si(t)=Si(t)-Si,  Si+1(t)=Si+1(t)-Si+1; Si+1(t)=Si+1(t)-Si+1;
Si и Si+1 – средние значения сигналов соседних i-го и (i+1)-го элементов, определенные на интервале Т;
Вi,i+1 – относительное смещение, затем определяют корректирующие коэффициенты элементов матрицы по чувствительности – 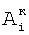 , и по смещению – , и по смещению – 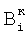 , i , i N, начиная с некоторого элемента в центре матрицы или непосредственной близости от центра – ему присваивают индекс 0 и этот элемент называют образующим 1-квадрат элементов матрицы (квадрат со стороной в 1 элемент), для «нулевого» элемента полагают N, начиная с некоторого элемента в центре матрицы или непосредственной близости от центра – ему присваивают индекс 0 и этот элемент называют образующим 1-квадрат элементов матрицы (квадрат со стороной в 1 элемент), для «нулевого» элемента полагают 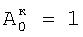 и и 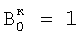 ; для каждого из четырех соседних «нулевому» элементов 3-квадрата (квадрата со стороной в 3 элемента) – их обозначают 1-элементы (см. фиг.1) по числу путей в эти элементы из «нулевого» элемента и называют следующими из «нулевого» элемента, полагают) ; для каждого из четырех соседних «нулевому» элементов 3-квадрата (квадрата со стороной в 3 элемента) – их обозначают 1-элементы (см. фиг.1) по числу путей в эти элементы из «нулевого» элемента и называют следующими из «нулевого» элемента, полагают) 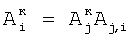 и и 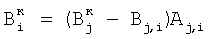 где индекс i проходит по 1-элементам, a j=0; для каждого из четырех 2-элементов (по числу путей в эти элементы из «нулевого» элемента) 3-квадрата, следующих из 1-элементов, полагают где индекс i проходит по 1-элементам, a j=0; для каждого из четырех 2-элементов (по числу путей в эти элементы из «нулевого» элемента) 3-квадрата, следующих из 1-элементов, полагают
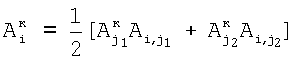 , ,
 , ,
где индекс i проходит по 2-элементам, индексы j1 и j2 соответствуют паре элементов, предшествующих i-му элементу, а номера i-х элементов, равные 2, берут равными сумме номеров предшествующих элементов; определяют корректирующие коэффициенты восьми 2-элементов периметра 5-квадрата, следующих из 2-элементов 3-квадрата: 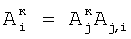 и и  , где индекс i соответствует следующим элементам, а индекс j – предшествующим, номер 2 i-м элементам присваивают по номерам предшествующих элементов; определяют корректирующие коэффициенты 5-элементов периметра 5-квадрата, каждому из которых предшествует три элемента и каждый из которых связан с «нулевым» элементом по пяти путям, по формулам , где индекс i соответствует следующим элементам, а индекс j – предшествующим, номер 2 i-м элементам присваивают по номерам предшествующих элементов; определяют корректирующие коэффициенты 5-элементов периметра 5-квадрата, каждому из которых предшествует три элемента и каждый из которых связан с «нулевым» элементом по пяти путям, по формулам
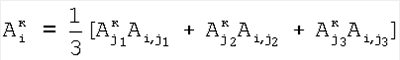 , ,
 , ,
где индекс i проходит по 5-элементам, индексы j1, j2 и j3 проходят по предшествующим элементам, номер 5 i-м элементам присваивают по сумме номеров предшествующих элементов; определяют корректирующие коэффициенты 4-элементов периметра 5-квадрата по формулам для случая двух предшествующих элементов; определяют корректирующие коэффициенты 5-элементов периметра 7-квадрата, следующие из 5-элементов периметра 5-квадрата; определяют корректирующие коэффициенты остальных элементов периметра 7-квадрата в порядке: 7-элементы, 11-элементы, 22-элементы; определяют корректирующие коэффициенты периметра 9-квадрата в порядке: 22-элементы, следующие из 22-элементов периметра 7-квадрата, 33-элементы, 40-элементы, 44-элементы, 85-элементы; по элементам периметра 9-квадрата с максимальным номером 85 определяются корректирующие коэффициенты следующих из них элементов периметра следующего, 11-квадрата, которым присваивается тот же номер; определяют корректирующие коэффициенты остальных элементов периметра 11-квадрата в порядке влево и вправо и вверх и вниз от 85-элементов; из элементов периметра 11-квадрата с максимальным номером – восьми угловых элементов, определяют следующие из этих элементов восемь элементов периметра 13-квадрата; по этим восьми элементам определяют угловые элементы 13-квадрата и по направлениям вверх-вниз и влево-вправо от этих восьми элементов определяют остальные элементы периметра 13-квадрата; определяют по элементам периметра 13-квадрата с максимальным номером – эти элементы находятся в середине сторон периметра, следующие из них элементы с таким же номером в 15-квадрате; определяют остальные элементы периметра 15-квадрата; определяют элементы с максимальным номером в 15-квадрате – они находятся в углах, определяют следующие из них элементы периметра 17-квадрата, определяют остальные элементы периметра 17-квадрата; определяют элементы 17-квадрата с максимальным номером, по ним определяют элементы с тем же номером 19-квадрата и так далее определяют элементы периметров квадратов увеличивающейся размерности, пока не будет достигнута одна или более границ матрицы, начиная откуда множество определяемых элементов наращивают только в трех или менее направлениях возможных движений от определенных к неопределенным элементам и так действуют до определения корректирующих коэффициентов всех элементов матрицы, отличающийся тем, что когда определяют отношения чувствительностей и относительные смещения соседних элементов из линейной регрессии выборки отсчетов сигналов S1(t), t=1, 2, …, Т по выборке Si+1(t), t=1, 2, …, Т и линейной регрессии отсчетов Si+1(t) no Si(t), для соседних в матрице элементов по вертикали в качестве Si(t) берут измененные отсчеты 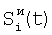 , которые получают по формуле , которые получают по формуле 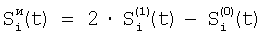 , и в качестве Si+1(t) берут, , и в качестве Si+1(t) берут, 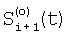 а для соседних в матрице элементов по горизонтали в качестве Si(t) берут отсчеты а для соседних в матрице элементов по горизонтали в качестве Si(t) берут отсчеты 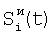 , которые получают по формуле , которые получают по формуле 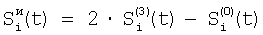 , и в качестве Si+1(t) берут , и в качестве Si+1(t) берут 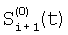 , где величины , где величины 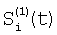 и и 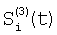 – отсчеты фотоприемного устройства с микросканированием со сдвигом изображения сцены на полэлемента матрицы вверх – отсчеты – отсчеты фотоприемного устройства с микросканированием со сдвигом изображения сцены на полэлемента матрицы вверх – отсчеты 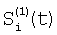 , и со сдвигом на полэлемента вправо – отсчеты , и со сдвигом на полэлемента вправо – отсчеты 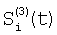 , относительно некоторого положения изображения – отсчеты , относительно некоторого положения изображения – отсчеты 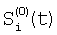 . .
РИСУНКИ
|
|