|
|
(21), (22) Заявка: 2007119488/09, 25.05.2007
(24) Дата начала отсчета срока действия патента:
25.05.2007
(46) Опубликовано: 10.03.2009
(56) Список документов, цитированных в отчете о
поиске:
RU 2029435 С1, 20.02.1995. RU 2025897 C1, 30.12.1994. SU 1633495 A1, 07.03.1991. SU 1737442 A1, 30.05.1992. JP 11282349 A, 15.10.1999. EP 0308963 A2, 29.03.1989.
Адрес для переписки:
355009, Ставропольский край, г. Ставрополь, ул. Пушкина, 1, научно-исследовательская часть
|
(72) Автор(ы):
Петренко Вячеслав Иванович (RU),
Сидорчук Алеся Вячеславна (RU)
(73) Патентообладатель(и):
Государственное образовательное учреждение высшего профессионального образования “Ставропольский государственный университет” (RU)
|
(54) ВЫЧИСЛИТЕЛЬНОЕ УСТРОЙСТВО
(57) Реферат:
Вычислительное устройство относится к вычислительной технике и может быть использовано в цифровых вычислительных устройствах, а также в устройствах цифровой обработки сигнала и в криптографических приложениях. Техническим результатом является расширение функциональных возможностей устройства за счет обеспечения формирования неполного частного. Устройство содержит 2n-2 сумматоров и n-1 мультиплексоров. 1 ил.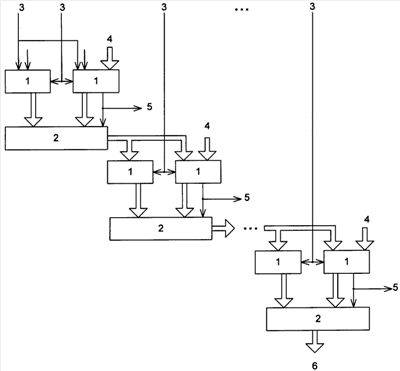
Изобретение относится к вычислительной технике и может быть использовано в цифровых вычислительных устройствах, а также в устройствах цифровой обработки сигналов и в криптографических приложениях.
Известно устройство для формирования остатка по произвольному модулю от числа, содержащее регистры, элементы ИЛИ, вычислитель, схемы сравнения, мультиплексор, элемент задержки, сумматор, группу блоков элементов И и блок постоянной памяти со связями (см. АС СССР №1633495, кл. Н03М 7/18, 1991).
Недостатком известного устройства является низкая надежность, так как для его реализации требуется большой объем оборудования.
Наиболее близким по технической сущности к заявляемому изобретению является комбинационный рекуррентный формирователь остатков, содержащий комбинационный формирователь частичных остатков, блок ключей и блок сумматоров по модулю (см. патент РФ №2029435, кл. 6 Н03М 7/18, 20.02.1995, бюл. №5).
Недостатком данного устройства являются его ограниченные функциональные возможности, а именно отсутствие возможности формирования неполного частного.
Цель изобретения – расширение функциональных возможностей устройства за счет обеспечения формирования неполного частного.
Для достижения поставленной цели в вычислительном устройство, содержащее 2n-2 сумматоров и n-1 мультиплексоров, где n – разрядность входного числа, (n-2-i)-й разряд двоичного кода входного числа подается на входы переносов первого и второго сумматоров i-й ступени преобразования, где i=1, …, n-1, а старший (n-1)-й разряд двоичного кода входного числа, сдвинутый на один разряд в сторону старшего, подается на первые входы первого и второго сумматоров первой ступени преобразования, на второй вход второго сумматора каждой ступени преобразования подается дополнительный двоичный код модуля, причем информационные входы i-го мультиплексора, где i=1, …, n-1 номер ступени преобразования, соединены с выходами первого и второго сумматоров i-й ступени преобразования, выход переноса второго сумматора i-й ступени преобразования соединен с управляющим входом i-го мультиплексора и является выходом (n-i-1)-го разряда неполного частного устройства, выход i-го мультиплексора, где i=1, …, n-2 номер ступени преобразования, соединен с первыми входами первого и второго сумматоров (i+1)-й ступени преобразования, причем j-й разряд мультиплексора, где j=1, …, n, соединен с (j+1)-м разрядом первого и второго сумматоров, выход (n-1)-го мультиплексора является выходом вычислительного устройства.
Сущность изобретения заключается в реализации следующего способа формирования остатка по произвольному модулю.
Пусть требуется сформировать остаток r от числа А по модулю р и вычислить частное q, то есть решить уравнение A=qp+r.
Число А может быть представлено в позиционной системе счисления в виде
А=an-12n-1+an-22n-2+an-32n-3+…+a222+a121+a020, где ai, 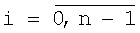 – коэффициенты, принимающие значения 0 или 1, n – количество разрядов в представлении числа А. Это выражение может быть представлено в следующем виде: – коэффициенты, принимающие значения 0 или 1, n – количество разрядов в представлении числа А. Это выражение может быть представлено в следующем виде:

Из теории чисел известно, что операция приведения по модулю инвариантна к сложению и умножению, т.е. величина остатка не зависит от того, вычислен он от суммы (произведения) или от каждого слагаемого (сомножителя), а затем соответствующие частичные остатки просуммированы (перемножены) и от результата вычислен остаток по модулю.
В таком виде значительно облегчается задача нахождения остатка r от числа A.
При проведении вычислений по модулю р значение выражения (2аn-1+аn-2) сравнивается с модулем р, где n количество разрядов числа А. Если значение (2аn-1+аn-2)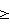 р, то из числа (2аn-1+аn-2) вычитается значение модуля р, то есть t1=(2аn-1+аn-2)-р. При этом формируется ненулевой старший (n-1)-й разряд неполного частного q. Если (2аn-1+аn-2)<р, то число (2аn-1+аn-2) остается без изменений t1=2аn-1+аn-2, а значение старшего (n-1)-го разряда неполного частного q принимается равным нулю. Полученное в результате значение t1 умножается на 2, складывается с аn-3 и сравнивается со значением р. Если значение (2t1+аn-3) р, то из числа (2аn-1+аn-2) вычитается значение модуля р, то есть t1=(2аn-1+аn-2)-р. При этом формируется ненулевой старший (n-1)-й разряд неполного частного q. Если (2аn-1+аn-2)<р, то число (2аn-1+аn-2) остается без изменений t1=2аn-1+аn-2, а значение старшего (n-1)-го разряда неполного частного q принимается равным нулю. Полученное в результате значение t1 умножается на 2, складывается с аn-3 и сравнивается со значением р. Если значение (2t1+аn-3)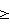 р, то из (2t1+an-3) вычитается значение модуля р, то есть t2=(2t1+аn-3)-р, при этом формируется ненулевой (n-2)-й разряд неполного частного q. Если (2t1+an-3) р, то из (2t1+an-3) вычитается значение модуля р, то есть t2=(2t1+аn-3)-р, при этом формируется ненулевой (n-2)-й разряд неполного частного q. Если (2t1+an-3)
1+an-3) остается без изменений t2=(2t1+аn-3), а значение (n-2)-го разряда неполного частного q принимается равным нулю. Полученное в результате значение t2 умножается на 2, складывается с аn-4 и сравнивается со значением р и т.д. На последнем (n-1)-м шаге число (2tn-2+а0) сравнивается с модулем р. Если значение (2tn-2+а0)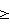 р, то из (2tn-2+а0) вычитается значение числа р, то есть tn-1=(2tn-2+а0)-р, при этом формируется ненулевой младший разряд неполного частного q. Если (2tn-2+а0) р, то из (2tn-2+а0) вычитается значение числа р, то есть tn-1=(2tn-2+а0)-р, при этом формируется ненулевой младший разряд неполного частного q. Если (2tn-2+а0)
n-2+а0) остается без изменений tn-1=2tn-2+а0, а значение младшего разряда неполного частного q принимается равным нулю. Полученное в результате значение r=tn-1 является остатком от деления числа А на число р. Операция умножения на два во всех случаях осуществляется сдвигом всех разрядов множимого на один в сторону старших. Суммирование осуществляется обычным способом с применением комбинационных двоичных сумматоров.
,>,>
На чертеже представлена схема вычислительного устройства.
Вычислительное устройство содержит 2n-2 сумматоров 1 и n-1 мультиплексоров 2, где n-разрядность входного числа, (n-2-i)-й разряд двоичного кода входного числа подается на входы 3 переносов первого и второго сумматоров 1 i-й ступени преобразования, где i=1, …, n-1, а старший (n-1)-й разряд двоичного кода входного числа, сдвинутый на один разряд в сторону старшего, подается на первые входы 3 первого и второго сумматоров 1 первой ступени преобразования, на второй вход 4 второго сумматора 1 каждой ступени преобразования подается дополнительный двоичный код модуля, причем информационные входы i-го мультиплексора 2, где i=1, …, n-1 номер ступени преобразования, соединены с выходами первого и второго сумматоров 1 i-й ступени преобразования, выход переноса второго сумматора 1 i-й ступени преобразования соединен с управляющим входом i-го мультиплексора и является выходом 5 (n-i-1)-го разряда неполного частного устройства, выход i-го мультиплексора, где i=1, …, n-2 номер ступени преобразования, соединен с первыми входами первого и второго сумматоров 1 (i+1)-й ступени преобразования, причем j-й разряд мультиплексора 2, где j=1, …, n, соединен с (j+1)-м разрядом первого и второго сумматоров 1, выход 6 (n-1)-ого мультиплексора является выходом вычислительного устройства.
Вычислительное устройство работает следующим образом.
На первые входы первых двух сумматоров 1 со входа 3 подается сигнал со старшего (n-1)-го разряда двоичного кода числа А, умноженный на 2, где n равно количеству разрядов двоичного представления числа А. На второй вход второго сумматора 1 со входа 4 подается дополнительный двоичный код РД модуля р. На входы переноса первых двух сумматоров подается сигнал с (n-2)-го разряда двоичного кода числа А. Первый сумматор 1 выполняет операцию (2аn-1+an-2), второй сумматор 1 выполняет операцию (2an-1+an-2+pд). Сигнал со старшего (k+1)-го разряда полученного значения, где k количество разрядов дополнительного двоичного кода модуля р, поступает на выход переноса второго сумматора 1. Остальные разряды представляют собой разность ((2аn-1+аn-2)-р). На первый вход первого мультиплексора 2 поступает информационный сигнал с первого сумматора 1, а на второй вход – информационный сигнал со второго сумматора 1. Если сигнал на выходе переноса второго сумматора 1 равен “1”, то на первый вход первого сумматора 1 второй ступени преобразования и на первый вход второго сумматора 1 второй ступени преобразования поступает разность t1=((2аn-1+аn-2)-р), если же он равен “0”, то на первый вход первого сумматора 1 и на первый вход второго сумматора 1 поступает число t1=(2аn-1+аn-2). На входы переноса обоих сумматоров 1 второй ступени преобразования подается (n-3)-й разряд двоичного кода числа А. На второй вход второго сумматора 1 второй ступени преобразования подается дополнительный двоичный код модуля р. Первый сумматор 1 выполняет операцию (2t1+аn-3), второй сумматор 1 выполняет операцию (2t1+аn-3+Рд). Далее выполняются те же действия, что и на первой ступени преобразования. После проведения n-1 таких операций на выходе 6 окажется результат вычисления числа А по модулю р, а на выходах 5 – код неполного частного q.
Рассмотрим работу вычислительного устройства на примере.
Пусть A=2510=110012, p=710=1112, рд=0012, n=5. Первый сумматор первой ступени преобразования формирует значение 2аn-1+аn-2=10+1=11. Второй сумматор первой ступени преобразования формирует значение 2аn-1+аn-2+рд=10+1+001=100. Старший 4-й разряд полученного значения равен 0, следовательно, первый мультиплексор переводит на сумматоры второй ступени преобразования значение t1=(2аn-1+аn-2)=11 и 3-й разряд неполного частного q принимает значение 0. Первый сумматор второй ступени преобразования формирует значение 2t1+аn-3=110+0=110. Второй сумматор второй ступени преобразования формирует значение 2t1+аn-3+рд=110+0+001=111. Старший 4-й разряд полученного значения равен 0, следовательно, второй мультиплексор переводит на сумматоры третьей ступени преобразования значение t2=(2t1+аn-3)=110 и 2-й разряд неполного частного q принимает значение 0. Первый сумматор третьей ступени преобразования формирует значение 2t2+аn-4=1100+0=1100. Второй сумматор третьей ступени преобразования формирует значение 2t2+аn-4+рд=1100+0+001=1101. Старший 4-й разряд полученного значения равен 1, следовательно, третий мультиплексор переводит на сумматоры четвертой ступени преобразования значение t3=(2t2+an-4)-р=101 и 1-й разряд неполного частного q принимает значение 1. Первый сумматор четвертой ступени преобразования формирует значение 2t3+аn-5=1010+1=1011. Второй сумматор четвертой ступени преобразования формирует значение 2t3+аn-5+рд=1010+1+001=1100. Старший 4-й разряд полученного значения равен 1, следовательно, четвертый мультиплексор переводит на выход код значения t4=(2t3+аn-5)-р=100 и 0-й разряд неполного частного q принимает значение 1. В результате неполное частное имеет значение q=0012=310.
Формула изобретения
Вычислительное устройство, содержащее 2n-2 сумматоров и n-1 мультиплексоров, где n-разрядность входного числа, отличающееся тем, что (n-2-i)-й разряд двоичного кода входного числа подается на входы переносов первого и второго сумматоров i-й ступени преобразования, где i=1, …, n-1, а старший (n-1)-й разряд двоичного кода входного числа, сдвинутый на один разряд в сторону старшего, подается на первые входы первого и второго сумматоров первой ступени преобразования, на второй вход второго сумматора каждой ступени преобразования подается дополнительный двоичный код модуля, причем информационные входы i-го мультиплексора, где i=1, …, n-1 номер ступени преобразования, соединены с выходами первого и второго сумматоров i-й ступени преобразования, выход переноса второго сумматора i-й ступени преобразования соединен с управляющим входом i-го мультиплексора и является выходом (n-i-1)-го разряда неполного частного устройства, выход i-го мультиплексора, где i=1, …, n-2 номер ступени преобразования, соединен с первыми входами первого и второго сумматоров (i+1)-й ступени преобразования, причем j-й разряд мультиплексора, где j=1, …, n, соединен с (j+1)-м разрядом первого и второго сумматоров, выход (n-1)-ого мультиплексора является выходом вычислительного устройства.
РИСУНКИ
|
|