|
|
(21), (22) Заявка: 2007129443/28, 31.07.2007
(24) Дата начала отсчета срока действия патента:
31.07.2007
(46) Опубликовано: 27.02.2009
(56) Список документов, цитированных в отчете о
поиске:
RU 2200940 С2, 20.03.2003. RU 2112227 С1, 27.05.1998. WO 9606339 А1, 29.02.1996. RU 2115904 С1, 20.07.1998. RU 2262678 С2, 20.10.2005. SU 1262318 А1, 07.10.1986.
Адрес для переписки:
197101, Санкт-Петербург, Кронверкский пр., 49, ГОУВПО “СПбГУ ИТМО” ОИС и НТИ
|
(72) Автор(ы):
Мельников Виталий Геннадьевич (RU)
(73) Патентообладатель(и):
Государственное образовательное учреждение высшего профессионального образования “Санкт-Петербургский государственный университет информационных технологий, механики и оптики” (RU)
|
(54) СПОСОБ ОПРЕДЕЛЕНИЯ ТЕНЗОРА ИНЕРЦИИ И КООРДИНАТ ЦЕНТРА МАСС ТЕЛА И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ
(57) Реферат:
Изобретение относится к измерительной технике и может быть использовано в машиностроении для определения осевых моментов инерции, тензоров инерции и центров масс тел. Способ заключается в том, что телу в условиях существенной диссипации энергии сообщается программное сферическое реверсивное симметричное разгонно-тормозное движение с синхронно-пропорциональным изменением углов собственного вращения и прецессии, с двумя последовательно вводимыми коэффициентами пропорциональности, с углом поворота не менее 600° вокруг собственной горизонтальной оси вращения. По замерам работы активного крутящего момента на программном движении вычисляют матрицу тензора инерции и полярные координаты центра масс тела. Устройство для осуществления способа содержит двухосный карданов подвес со взаимно перпендикулярными осями вращения, с внутренней рамкой, имеющей цилиндрический кожух с возможностью закрепления в ней тела, управляемый электропривод, соосный с внешней рамкой, и передаточный механизм, содержащий пару цилиндрических зубчатых колес и муфту с двумя парами конических зубчатых колес. Технический результат заключается в повышении производительности, точности, расширения области применения. 2 н.п. ф-лы, 4 ил.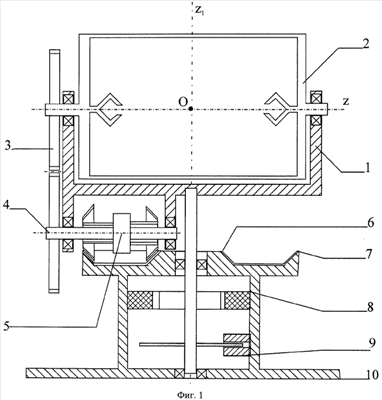
Изобретение относится к машиностроению и может быть использовано для определения осевых моментов инерции, тензоров инерции и центров масс тел на подвесах, вращающихся по заданной программе в условиях неизвестного трения и аэродинамического сопротивления с возможностью синхронно-пропорционального вращения двух рамок подвеса.
Известен способ определения момента и тензора инерции тела (Патент РФ №2112227, МПК G01М 1/10, дата приоритета 20.07.94 опубл. 27.05.98, Бюл. №15), при котором платформе с произвольно направленной в пространстве осью вращения, установленной в опоре с закрепленным на ней телом, сообщают моментом сил в виде разгонно-тормозного момента любой физической природы, не принимающих близких к нулю значений, однонаправленное динамически квазисимметрическое относительно положения равновесия двухэтапное вращение, имеющее этап разгона с существенно отличным от нуля угловым ускорением, резко переходящим в почти симметричный ему этап торможения, измеряют конечное множество значений угловой скорости платформы в определенных угловых положениях, симметричных относительно положения статического равновесия системы платформа-тело, изменяют на известную переменную величину, удовлетворяющую определенным условиям, приложенный момент и повторно измеряют мгновенные угловые скорости, по которым аналитически определяют осевой момент инерции тела, а после шести испытаний относительно различно направленных осей вращения аналитически определяют тензор инерции тела.
Недостатками способа являются невысокие точность и производительность, связанные с тем, что необходимо знать или определять в условиях трения положение статического равновесия системы, соответствующее наиболее низкому положению центра масс, перенастраивать устройство, производить повторное испытание.
Известен способ определения тензора инерции тела с одновременным определением координат центра масс тела (Патент РФ №2262678, МПК G01М 1/10, дата приоритета 16.07.02, опубл. 20.10.2005, Бюл. №29), по которому тело устанавливают на платформу с осью вращения, сообщают этой системе программное замедленное вращение в ограниченной произвольно выбранной угловой зоне и обратное симметричное ускоренное вращение в этой же зоне, повторяющее в обратном порядке замедленное вращение с угловой скоростью противоположного знака, определяют приложенный активный вращающий момент и угловую скорость на множестве угловых положений системы, по которым аналитически определяют осевой момент инерции и две координаты центра масс, и по шести аналогичным испытаниям, производимым при различных угловых положениях тела на платформе, определяют тензор инерции в точке тела и расположение центра масс тела.
Недостатком способа является невысокая производительность и точность, связанная с тем, что приходится выполнять шесть испытаний, разделенных переходными процессами остановок, перевода тела на платформе в новые угловые положения и шестикратное выведение тела на программные движения.
Наиболее близким к изобретению является способ определения тензора инерции тела (Патент РФ №2200940, МПК G01М 1/10, дата приоритета 19.07.00, опубл. 20.03.2003, Бюл. №8), при котором платформе с произвольно направленной осью вращения, установленной в подшипниковой опоре, в условиях неизвестного трения и неизвестного положения центра масс тела активным моментом сил любой физической природы сообщают реверсивно симметричное движение, содержащее полный тормозной оборот с постепенно убывающей по величине угловой скорости и полный разгонный оборот в обратном направлении, повторяющий в обратном порядке тормозной оборот с угловой скоростью противоположного знака, с допускаемым переходным процессом между двумя оборотами, измеряют множество значений активного вращающего момента, по которым определяют момент инерции тела, и по моментам инерции относительно шести различно направленных осей определяют тензор инерции тела и одновременно с ним аналитически определяют центр масс тела.
Недостатками способа являются невысокие производительность и точность, связанные с тем, что тензор инерции тела определяется на шести испытаниях, разделенных процедурами установления и фиксации тела на платформе в шести различных угловых положениях.
Известно устройство для определения тензора и момента инерции изделия (Патент РФ №2112227, МПК G01М 1/10, дата приоритета 20.07.94, опубл. 27.05.1998, Бюл. №15), содержащее платформу с произвольно расположенной в пространстве осью вращения, установленной в неподвижных подшипниковых опорах, захват для закрепления в нем тела, взаимодействующим посредством муфты со стержнем силовой механизм, выполненный в виде упругого четырехпружинного механизма, одна пара пружин которого выполнена в виде предварительно сжатых регулируемыми упорами пружин, контактирующих со стержнем муфты, другая пара пружин работает в пределах двух измерительных интервалах и выключена при повторном испытании.
Недостатками способа являются невысокие производительность и точность, обусловленные тем, что неточно учитывается трение, неточно и медленно определяется положение статического равновесия системы тело-платформа в условиях трения, от которого в дальнейшем производится отсчет угла поворота, система вручную или дополнительным приводом выводится из положения равновесия, требуется перенастройка пружинного механического привода и проведение повторного испытания; устройство не предназначено для одновременного определения центра масс тела.
Наиболее близким к изобретению устройства является устройство для определения тензора инерции тела (Патент РФ №2200940, МПК G01М 1/10, дата приоритета 19.07.00, опубл. 20.03.2003, Бюл. №8), содержащее платформу с валом, установленным в подшипниковой опоре, вал с захватом для закрепления тела, установленным на платформе с возможностью его поворота и фиксации в определенных угловых положениях, датчик угла поворота и угловой скорости платформы, автоматизированный электропривод, содержащий электродвигатель и переключатель вращения вала платформы на вращение вала захвата, выполненный в виде конической зубчатой передачи и двух фрикционных электромуфт.
Недостатками устройства являются невысокая производительность и точность, обусловленные тем, что оно предназначено для осуществления способа с недостаточной производительностью, содержит последовательность переключений вращения тела с одной оси на другую и обратно, с переходными процессами во время остановок, перевода тела в требуемое угловое положение в переключенном режиме и разгона до требуемой начальной угловой скорости.
Решается задача повышения производительности, точности, расширения области применения на системах программного управления, способных исполнять программные неравномерные симметричные движения вокруг неподвижной точки, с постоянным углом нутации вектора угловой скорости, неравномерным изменением угла прецессии и синхронно-пропорциональным с ним изменением угла собственного вращения.
Сущность изобретения и заключается в том, что телу, установленному в двухосном кардановом подвесе в условиях неизвестных трения в подшипниках, сопротивления среды и расположения в теле центра масс сообщают реверсивное симметричное сферическое прецессионное движение вокруг неподвижной точки (РСП-движение), содержащее замедленное вращение по углу прецессии вокруг вертикальной оси внешней рамки, переходящее (с допускаемым переходным процессом выбега) в ускоренное вращение в обратном направлении с повторением в обратном порядке замедленного вращения. Одновременно внутренней рамке карданова подвеса, снабженного цилиндрическим кожухом с установленным в ней телом, сообщают реверсивно-симметричное собственное вращательное движение, синхронное с прецессионным движением, с определенным постоянным отношением угла прецессии к углу собственного вращения с наблюдаемым изменением угла собственного вращения на интервале 0-600°, отсчитываемого от любого выбранного углового положения, затем повторяют испытание с другим постоянным значением коэффициента пропорциональности. На таком программном сферическом движении тела замеряют множество значений работы активного крутящего момента, либо замеряют работы этого момента, по которым аналитически определяют тензор инерции тела в точке пересечения осей вращения и координаты центра масс тела.
Изобретение поясняют фиг.1-4, где на фиг.1 показано устройство для осуществления метода в виде двухосного карданова подвеса с взаимно перпендикулярными осями и электроприводом, осуществляющим тестирующее двухосное синхронное сферическое движение с двумя последовательными значениями коэффициента пропорциональности, на фиг.2 показано одно из рекомендуемых к применению тестирующих движений по углу собственного вращения с которым синхронизировано прецессионное вращение, с двумя значениями коэффициентов пропорциональности, на фиг.3 показан выбор значений этих коэффициентов пропорциональности из условия двух заданных значений угла отклонения вектора угловой скорости сферического движения от собственной оси рамки подвеса, на фиг.4 показаны шесть ортов осей виртуального икосаэдра, условно связанного с тестируемым телом, проходящих через точку пересечения осей карданова подвеса.
Устройство (фиг.1) содержит двухосный карданов подвес, состоящий из внешней рамки 1 с вертикальной осью вращения Oz1 и внутренней рамки с цилиндрическим кожухом 2 с горизонтальной осью вращения Oz, механизм передачи вращения с вала внешней рамки на вал внутренней рамки, выполненный в виде пары цилиндрических зубчатых колес 3-4 и конической муфты 5, обеспечивающей поочередное сцепление конических колес с двумя неподвижными коническими колесами 6-7, управляемый электродвигатель 8, датчик угла поворота внешней рамки 9, основание 10. Внутренняя рамка подвеса 2 снабжена цилиндрическим кожухом с целью обеспечения независимости момента сопротивления среды от направления вращения карданова подвеса.
Реверсивно-симметричной синхронной прецессией тела, или РСП-движением, назовем сферическое движение тела вокруг закрепленной точки, при котором угол нутации остается постоянным, равным 90°, угол собственного вращения изменяется неравномерно реверсивно-симметрично в пределах 600°, нарастает замедленно в положительном направлении и симметрично убывает при движении в обратном направлении, а угол прецессии изменяется синхронно-пропорционально с изменением угла собственного вращения. При этом прецессионное движение производится вокруг вертикальной оси, а собственное вращение – вокруг подвижной горизонтальной оси. Будут применены два РСП-движения с двумя значениями коэффициента пропорциональности, объединенные переходным процессом в одно движение.
В способе используются измеряемые значения активного крутящего момента на программном РСП-движении, либо значения работы крутящего момента (полезного расхода энергии.
Сущность способа заключается в том, что твердому телу, размещенному в двухосном кардановом подвесе со взаимно перпендикулярными осями вращения, сообщают последовательно программное РСП – движение в условиях неизвестного трения, отсчитываемое от произвольно выбираемого углового положения, содержащее этап ускоренного вращения в угле 600° по углу собственного вращения  с синхронным пропорциональным поворотом по углу прецессии с синхронным пропорциональным поворотом по углу прецессии  = = 1,2 1,2 и замедленное обратное симметричное движение, повторяющее в обратном порядке ускоренное движение, с соответствующими отрицательными значениями скалярной угловой скорости. Переход на второе значение коэффициента и замедленное обратное симметричное движение, повторяющее в обратном порядке ускоренное движение, с соответствующими отрицательными значениями скалярной угловой скорости. Переход на второе значение коэффициента  можно выполнять на ходу, на малых угловых скоростях, либо после остановки устройства. можно выполнять на ходу, на малых угловых скоростях, либо после остановки устройства.
Программное сферическое реверсивно-симметричное движение тела и прямо пропорциональное ему прецессионное вращение
В качестве РСП-движения по углу собственного вращения  на интервале [0,600°] можно принять равнозамедленное, равноускоренное движение с постоянным отрицательным ускорением на интервале [0,600°] можно принять равнозамедленное, равноускоренное движение с постоянным отрицательным ускорением 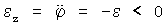 при при  =const>0, начинающееся с положительного значения угловой скорости =const>0, начинающееся с положительного значения угловой скорости  0, задаваемое уравнением 0, задаваемое уравнением
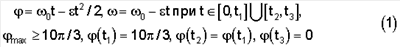
При этих условиях назначаем
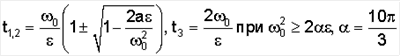
Такое движение с момента времени tp= 0/ 0/ автоматически переходит из тормозного в разгонное в обратном направлении. Целесообразно рассматривать движение на интервалах времени, не включающих момент реверса tр, т.е. взять t1p. автоматически переходит из тормозного в разгонное в обратном направлении. Целесообразно рассматривать движение на интервалах времени, не включающих момент реверса tр, т.е. взять t1p.
Можно также применять равноускоренное движение вида
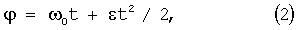
которое после переключения и реверса переходит в симметричное равнозамедленное движение.
Другим примером РСП-движения может служить половина колебания, выполняемого согласно уравнению
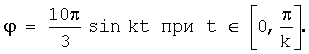
А также рекомендуется к применению движение в виде пары симметричных частей на первой половине колебания вида
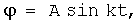 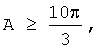 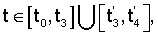
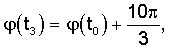 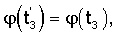 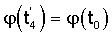
Одновременно с «собственным» программным вращением тела вокруг некоторой выбранной оси Oz должно осуществляться «прецессионное» вращение этой оси тела вокруг вертикальной оси Oz1, прямо пропорциональное собственном вращению. В целом телу придается сферическое движение вокруг неподвижной точки, разбиваемое на два синхронных вращательных РСП-движения.
На фиг.2 показано РСП-движение, состоящее из разгона по параболическому закону на интервале времени [t1, t6] при t1=0,  (t1)=0, (t1)=0,  (t6)=600°, плавно переходящее в движение реверса по другому параболическому закону, и затем в обратное симметричное тормозное движение на интервале (t6)=600°, плавно переходящее в движение реверса по другому параболическому закону, и затем в обратное симметричное тормозное движение на интервале 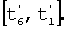 Дальнейшим продолжением движения является медленный переходный процесс на интервале Дальнейшим продолжением движения является медленный переходный процесс на интервале 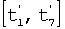 c переключением на ходу коэффициента связи c переключением на ходу коэффициента связи  угла прецессии угла прецессии  со значения со значения  1 на 1 на  2 и с выходом на повторное движение с новым значением коэффициентом 2 и с выходом на повторное движение с новым значением коэффициентом  2. 2.
Рассмотрим управляемую электромеханическую систему (Фиг.1), состоящую из платформы 2 с закрепленном в ней телом, совершающей программное движение по углу  вокруг подвижной горизонтальной оси Oz и второй системы – электропривода, обеспечивающего вращение оси Oz вокруг оси O вокруг подвижной горизонтальной оси Oz и второй системы – электропривода, обеспечивающего вращение оси Oz вокруг оси O с ортом k1 по углу с ортом k1 по углу  . Изменение углов . Изменение углов  и и  назначается синхронным прямо пропорциональным, причем коэффициенту пропорциональности сначала придаем значение назначается синхронным прямо пропорциональным, причем коэффициенту пропорциональности сначала придаем значение  1, а затем 1, а затем  2 2
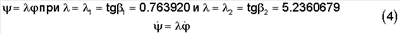
Здесь  1 и 1 и  2 – требуемые углы наклона мгновенной угловой скорости 2 – требуемые углы наклона мгновенной угловой скорости 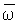 к оси собственного вращения тела (фиг.3), обеспечивающие последовательное совпадение ее положения с осями виртуального икосаэдра, имеющие следующие значения: к оси собственного вращения тела (фиг.3), обеспечивающие последовательное совпадение ее положения с осями виртуального икосаэдра, имеющие следующие значения:  1=0.6524 рад = 37.38°, 1=0.6524 рад = 37.38°,  2=1.3821 рад = 79.19°. 2=1.3821 рад = 79.19°.
Система тело-платформа совершает сферическое движение вокруг вертикальной оси с углом прецессии  , углом собственного вращения , углом собственного вращения  , постоянным углом нутации , постоянным углом нутации  =90°. Угловая скорость этого движения =90°. Угловая скорость этого движения
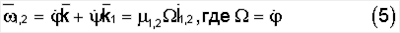
где 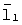 и и 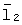 – орты угловых скоростей – орты угловых скоростей 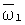 и и 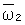
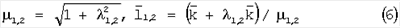
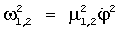 при при 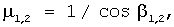 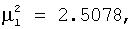 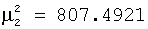
Это движение назовем прецессионным движением вокруг вертикальной оси, оно определяется одним уравнением вида  = = (t), т.е. программным уравнением асимметричного прецессионного движения. Мгновенная ось вращения тела OL1 (OL2) вместе с вектором (t), т.е. программным уравнением асимметричного прецессионного движения. Мгновенная ось вращения тела OL1 (OL2) вместе с вектором 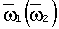 выполняет асимметричную прецессию вокруг вертикальной оси O выполняет асимметричную прецессию вокруг вертикальной оси O с постоянным углом нутации с постоянным углом нутации  1=90°- 1=90°- 1, ( 1, ( 2=90°- 2=90°- 2) согласно программному уравнению 2) согласно программному уравнению  = = 1 1 (t), ( (t), ( = = 2 2 (t)). Геометрической интерпретацией такой симметрической прецессии служит неравномерное разгонно-тормозное асимметричное качение кругового конуса с осью Oz, углом при вершине L1Oz= (t)). Геометрической интерпретацией такой симметрической прецессии служит неравномерное разгонно-тормозное асимметричное качение кругового конуса с осью Oz, углом при вершине L1Oz= 1, (L2Oz= 1, (L2Oz= 2) по неподвижному круглому конусу с вертикальной осью O 2) по неподвижному круглому конусу с вертикальной осью O с углом при вершине L1Oz= с углом при вершине L1Oz= 1, (L1Oz= 1, (L1Oz= 2). Будет использовано следующее свойство: на реверсивном симметричном сферическом движении при угле поворота 2). Будет использовано следующее свойство: на реверсивном симметричном сферическом движении при угле поворота  =600° и обратно каждая из трех осей виртуального икосаэдра через полный оборот совпадает четыре раза с мгновенной осью вращения OL1 при =600° и обратно каждая из трех осей виртуального икосаэдра через полный оборот совпадает четыре раза с мгновенной осью вращения OL1 при  = = 1, а три другие оси икосаэдра на втором движении совпадают четыре раза с OL2. 1, а три другие оси икосаэдра на втором движении совпадают четыре раза с OL2.
Введенное понятие симметричной прецессии является обобщением понятия регулярной прецессии (Бухгольц Н.Н. Основной курс теоретической механики. 4.2. М.: Наука, 1966. стр.161-162, Бесекерский В.А., Фабрикант Е.А. Динамический синтез систем гироскопической стабилизации. Л.: Судостроение, 1968. стр.18-23, Лурье А.И. Аналитическая механика. М: ФМ, 1961. стр.134).
На фиг.4 показаны четыре из двадцати треугольных граней виртуального икосаэдра, сцепляемого с тестируемым телом. Через вершины граней А, В, С, Е, G, F проведены все шесть осей икосаэдра с ортами осей 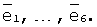 Стороны треугольника приняты равными единице, ось Oz направлена из центра икосаэдра на центр пересечения медиан одной из граней. Стороны треугольника приняты равными единице, ось Oz направлена из центра икосаэдра на центр пересечения медиан одной из граней.
Радиусы вписанной и описанной сфер
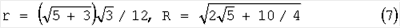
Расстояния от точки касания вписанной сферы до вершин грани АВС равны 2 , где , где 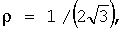 высота грани высота грани 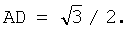
Имеем

Численные значения основных величин:
 1=52.622632°=0.9184382 рад, 1=52.622632°=0.9184382 рад,  2=10.812317°=0.1887105 рад, 2=10.812317°=0.1887105 рад,
 1=37.377368°=0.652358 рад, 1=37.377368°=0.652358 рад,  2=79.187685°=1.382086 рад, 2=79.187685°=1.382086 рад,
 =63.434949°=1.107149 рад, R=0.951057, r=0.755761, =63.434949°=1.107149 рад, R=0.951057, r=0.755761,
 =0.288675, b=ОК=0.934172, h=KE=0.178411 =0.288675, b=ОК=0.934172, h=KE=0.178411
Над плоскостью Oxy расположены шесть вершин икосаэдра. Вершины ABC расположены на уровне z1=r на окружности радиусом  1=2 1=2 =0.577350 с равными угловыми расстояниями 120°, а три вершины E, G, F расположены на уровне z2=h – на окружности радиуса =0.577350 с равными угловыми расстояниями 120°, а три вершины E, G, F расположены на уровне z2=h – на окружности радиуса  2=b. Через названные вершины и центр О проходят шесть осей икосаэдра. На фиг.4 показаны орты этих осей. Направляющие косинусы ортов равны отношениям координат вершин к расстоянию R. Векторы-строки ортов 2=b. Через названные вершины и центр О проходят шесть осей икосаэдра. На фиг.4 показаны орты этих осей. Направляющие косинусы ортов равны отношениям координат вершин к расстоянию R. Векторы-строки ортов
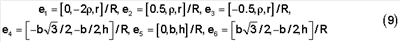
Шестиэлементные векторы-столбцы:
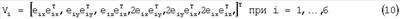
Из столбцов составим матрицу ортов осей икосаэдра размера 6×6:
U=[V1, V2, V3, V4, V5, V6]
Численное значение матрицы U:
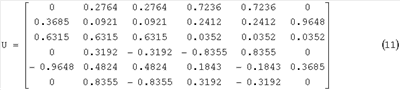
Определитель матрицы существенно отличен от нуля и равен det(U)=2.2897.
Пусть в результате эксперимента найдены шесть моментов инерции твердого тела относительно осей виртуального икосаэдра, жестко сцепленного с телом и имеющего центр в некоторой точке О тела. Тогда вектор-строка из осевых и центробежных моментов инерции тела вычисляется по следующей матричной формуле:
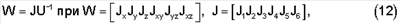
Рассмотрим систему, состоящую из двухосного карданова подвеса и установленного в нем тела (фиг.1). Ось вращения внешней рамки Oz1 вертикальна, а ось вращения внутренней рамки-платформы Oz движется в горизонтальной плоскости. На внутренней рамке жестко закреплено тестируемое тело. Подвес приводится в движение электродвигателем, вал которого жестко связан с внешней рамкой, а движение на внутреннюю рамку передается через зубчатый механизм. Будем считать, что внутренняя рамка-платформа имеет цилиндрический кожух, который обеспечивает равенство аэродинамического сопротивления в симметричных движениях. Вращение внутренней рамки определяется углом  , а внешней рамки – углом , а внешней рамки – углом  . Система тело-платформа совершает сферическое движение вокруг точки О пересечения осей подвеса. Предполагаем, что выполняется голономная связь вида . Система тело-платформа совершает сферическое движение вокруг точки О пересечения осей подвеса. Предполагаем, что выполняется голономная связь вида  = = 1(2) 1(2) . Тогда механическая голономная система: карданов подвес – ротор электродвигателя – передаточный механизм – тестируемое тело будет иметь только одну степень свободы, ее положение определяется одной обобщенной координатой – углом поворота . Тогда механическая голономная система: карданов подвес – ротор электродвигателя – передаточный механизм – тестируемое тело будет иметь только одну степень свободы, ее положение определяется одной обобщенной координатой – углом поворота  . .
Обозначим I – приведенный момент инерции по углу  системы без тестируемого тела. Очевидно I=const, поскольку расположение массы устройства вокруг оси внешней рамки не изменяется при изменении угла системы без тестируемого тела. Очевидно I=const, поскольку расположение массы устройства вокруг оси внешней рамки не изменяется при изменении угла  (или (или  ) (считаем, что внутренняя рамка и колеса обладают осевой симметрией). Неизвестный приведенный момент инерции тела J, совершающего сферическое движение, зависит от угла ) (считаем, что внутренняя рамка и колеса обладают осевой симметрией). Неизвестный приведенный момент инерции тела J, совершающего сферическое движение, зависит от угла  :J=J( :J=J( ). ).
В качестве РСП-движения по углу  примем кусочно-параболическое движение (фиг.2), содержащее этап разгона при t1, этап равноускоренного движения при t примем кусочно-параболическое движение (фиг.2), содержащее этап разгона при t1, этап равноускоренного движения при t [t1, t6] на угловом интервале 0 [t1, t6] на угловом интервале 0   600°, этап плавного переходного процесса по параболическому закону при 600°, этап плавного переходного процесса по параболическому закону при 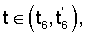 этап симметричного равнозамедленного параболического движения при этап симметричного равнозамедленного параболического движения при 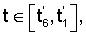 этап переходного процесса при этап переходного процесса при 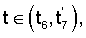 с переключением коэффициента с переключением коэффициента  со значения со значения  1 на 1 на  2 и повторного движения на интервале 2 и повторного движения на интервале 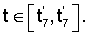 Движение по углу Движение по углу  осуществляется синхронно согласно кинематическому уравнению осуществляется синхронно согласно кинематическому уравнению
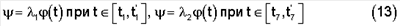
Квадрат полной угловой скорости сферического РСП-движения определяется формулой (6). На этапе разгон-торможение выделим три полных оборота, смещенных один относительно другого на 120°:
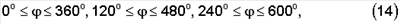
осуществляемых за интервал времени
 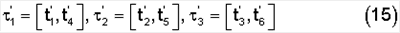
На обратном движении угловые интервалы (14) проходят в интервалы
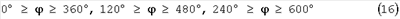
за промежутки
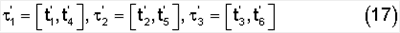
Пусть I1 – момент инерции всего устройства относительно оси z1. Имеем 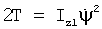 – кинетическая энергия механизма при изменении угла – кинетическая энергия механизма при изменении угла  и условно зафиксированном угле и условно зафиксированном угле  . Если же угол . Если же угол  изменяется с угловой скоростью изменяется с угловой скоростью 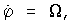 то внутренняя рамка совершает сферическое движение вокруг полюса О с переносной угловой скоростью то внутренняя рамка совершает сферическое движение вокруг полюса О с переносной угловой скоростью 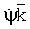 и относительной скоростью и относительной скоростью 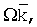 причем эти скорости взаимно перпендикулярны, а оси системы Oxyz являются главными осями инерции внутренней цилиндрической рамки. При этих условиях полная кинетическая энергия устройства определяется двучленной формулой причем эти скорости взаимно перпендикулярны, а оси системы Oxyz являются главными осями инерции внутренней цилиндрической рамки. При этих условиях полная кинетическая энергия устройства определяется двучленной формулой
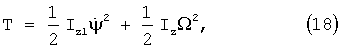
где Iz – момент инерции внутренней рамки относительно собственной оси, в которую включаем и моменты инерции колес передаточного механизма.
Кинетическая энергия тестируемого тела на сферическом движении
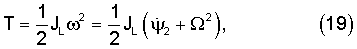
где JL – момент инерции тела относительно мгновенной оси вращения OL.
На основании формул (18), (19) определим кинетическую энергию системы механизм-тело, включая ротор электродвигателя и передаточный механизм, на двух движениях  = = 1 1 и и  = = 2 2 : :
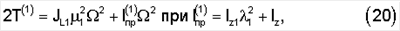

Здесь 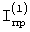 и и 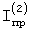 – приведенные моменты инерции механизма по углу поворота – приведенные моменты инерции механизма по углу поворота  на двух режимах движения, JL1( на двух режимах движения, JL1( ) и JL2( ) и JL2( ) – моменты инерции тела относительно мгновенных осей L1 и L2 сферического движения. ) – моменты инерции тела относительно мгновенных осей L1 и L2 сферического движения.
Применим теорему об изменении кинетической энергии к системе устройство-тело на паре интервалов  1=[t1, t4] и 1=[t1, t4] и 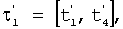 учитывая равенство энергий на концах интервалов учитывая равенство энергий на концах интервалов
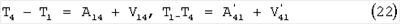
Здесь A14 и 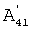 – работы активного крутящего момента, создаваемого электродвигателем, V14 и – работы активного крутящего момента, создаваемого электродвигателем, V14 и 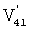 – работы моментов трения и аэродинамического сопротивления. – работы моментов трения и аэродинамического сопротивления.
Отметим, что 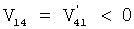 ввиду динамической симметрии пары движений, обеспеченной, в частности, наличием цилиндрического кожуха. Работы силы тяжести тела не входят в уравнения, они равны нулю, поскольку на рассматриваемых полных оборотах тела его центр масс возвращается на прежнюю горизонтальную эквипотенциальную поверхность независимо от угла поворота тела вокруг вертикальной оси Oz1. Почленно вычитая уравнения (22) и учитывая выражение (20), получим уравнение, не содержащее работы сил трения ввиду динамической симметрии пары движений, обеспеченной, в частности, наличием цилиндрического кожуха. Работы силы тяжести тела не входят в уравнения, они равны нулю, поскольку на рассматриваемых полных оборотах тела его центр масс возвращается на прежнюю горизонтальную эквипотенциальную поверхность независимо от угла поворота тела вокруг вертикальной оси Oz1. Почленно вычитая уравнения (22) и учитывая выражение (20), получим уравнение, не содержащее работы сил трения
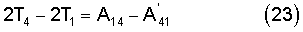
или
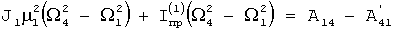
Отсюда находим расчетную формулу для момента инерции тела относительно первой оси икосаэдра, не содержащую диссипативных сил.
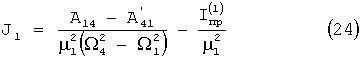
Рассмотрим аналогично две оставшиеся пары поворотов из (14) и (16), получаем расчетные формулы для двух других осей икосаэдра
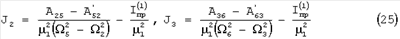
Моменты инерции относительно трех осей икосаэдра второго ряда определяются по аналогичным расчетным формулам
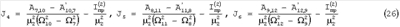
Приведенные моменты инерции устройства можно находить расчетом или посредством заранее выполненного эксперимента с ненагруженным механизмом при отсутствии тела по формулам
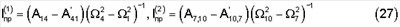
Формулы (27) служат для идентификации самого устройства.
Таким образом, тензор инерции тела в точке О пересечения двух осей карданова подвеса определяется формулами (12), (11), (24), (25), (26) с возможным привлечением формул. В этих формулах работы активного крутящего момента M( ) находятся через вычисление определенных интегралов от активного момента по углу поворота, ) находятся через вычисление определенных интегралов от активного момента по углу поворота,
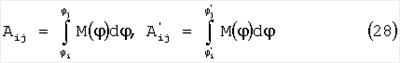
Возможно также непосредственное измерение этих работ техническими средствами по расходу энергии на работу механизма, включающую работу на преодоление диссипативных сил.
Расчетные формулы получены в предположении, что внутренняя рамка является симметричным телом вращения с осью симметрии Oz. В случае, если это условие не выполняется, можно определять по данным формулам осевые моменты инерции тела вместе с внутренней рамкой и затем вычитать осевые моменты инерции внутренней рамки при шести различных угловых положениях рамки.
Для определения центра масс тела разделим первый оборот (фиг.1), совершаемый за интервал времени  1=[t1, t4] на четверть, обороты, совершаемые за интервалы времени 1=[t1, t4] на четверть, обороты, совершаемые за интервалы времени
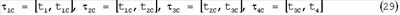
Рассмотрим полуоборот за интервал 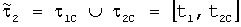 и другой полуоборот за интервал и другой полуоборот за интервал 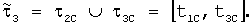 Предполагаем, что центр масс платформы расположен на ее собственной оси и m – известная масса системы тело-платформа. Введем в рассмотрение цилиндрические координаты ( Предполагаем, что центр масс платформы расположен на ее собственной оси и m – известная масса системы тело-платформа. Введем в рассмотрение цилиндрические координаты ( C, C,  , zC) неизвестного положения центра масс этой системы, где , zC) неизвестного положения центра масс этой системы, где  C – полярный радиус, C – полярный радиус,  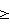 0 или 0 или  <0 – полярный угол, отсчитываемый от отвесного направления в начале эксперимента. Работа силы тяжести этой системы на интервалах <0 – полярный угол, отсчитываемый от отвесного направления в начале эксперимента. Работа силы тяжести этой системы на интервалах 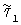 и и 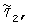 и работы на асимметричных полуоборотах: и работы на асимметричных полуоборотах:

По аналогии с формулой (23) составим два уравнения энергии для двух пар симметричных полуоборотов системы платформа-тело, в которые следует дополнительно включить разности работ сил тяжести 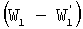 и и 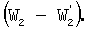
Получим
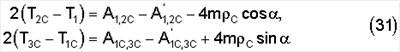
Здесь T1, Т1C, Т2C, Т3C – значения кинетической энергии системы на концах полуоборотов. Они считаются известными, поскольку известны программные значения угловых скоростей и уже вычислен тензор инерции системы тело-платформа, а также определены кинетические энергии системы в любых ее положениях по формуле сферического движения 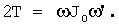
Из уравнений (31) находим два уравнения:
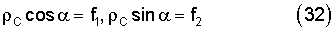
при

Из системы находим расчетные формулы, определяющие две цилиндрические координаты центра масс системы тело-платформа:

Формулы определяют прямую, параллельную собственной оси платформы Oz, на которой расположен центр масс системы тело-платформа, причем угол  отсчитывается от сечения тела отвесной плоскостью, проведенной в начальный момент времени t1 через ось собственного вращения. Координату zc, определяющую положение центра масс на этой прямой, можно найти произведя дополнительное испытание, расположив тело на внутренней платформе в повернутом положении, развернутом на угол 90° от оси Oz в горизонтальной плоскости (фиг.1). отсчитывается от сечения тела отвесной плоскостью, проведенной в начальный момент времени t1 через ось собственного вращения. Координату zc, определяющую положение центра масс на этой прямой, можно найти произведя дополнительное испытание, расположив тело на внутренней платформе в повернутом положении, развернутом на угол 90° от оси Oz в горизонтальной плоскости (фиг.1).
Устройство работает следующим образом: внутренняя рамка 2 карданова подвеса с закрепленным в ней телом исполняет программное сферическое движение вокруг неподвижной точки О, состоящее из прецессионного вращения вокруг оси Oz, создаваемое внешней рамкой 1 вместе с электродвигателем 8 и собственного вращения рамки вокруг оси Oz, создаваемого электроприводом, при этом датчиком 9 производится непосредственное измерение угла поворота и угловой скорости вращения ротора электродвигателя. Управление движением осуществляется автоматической системой программного управления. Электромуфта 5 на одном этапе фиксирует на валу 4 левое коническое зубчатое колесо, отпуская при этом правое коническое колесо, а на другом этапе наоборот, фиксирует на валу правое коническое колесо и отпускает левое колесо, чем достигается изменение коэффициента пропорциональности, связывающего прецессионное и собственное вращения платформы 2. В результате устройство обеспечивает телу требуемое программное сферическое движение.
Таким образом предполагаемое изобретение позволяет решить задачу повышения производительности, точности, расширения области применения.
Формула изобретения
1. Способ определения тензора инерции, заключающийся в том, что платформе с закрепленным на ней телом в условиях неизвестных трения, сопротивления среды и положения центра масс тела сообщают активным моментом сил симметричное реверсивное разгонно-тормозное вращение, отсчитываемое от произвольно выбранного углового положения, содержащее полный тормозной оборот с постепенно убывающей величиной угловой скорости и полный разгонный оборот в обратном направлении, повторяющий в обратном порядке тормозной оборот с угловой скоростью противоположного знака с допускаемым переходным процессом между оборотами, измеряют активный вращающий момент и угловые скорости платформы или измеряют работу активного момента на множестве угловых положений, по которым аналитически определяют осевой момент инерции тела и по моментам инерции относительно шести осей, направленных вдоль осей виртуального икосаэдра, условно связанного с телом, определяют тензор инерции тела и расположение центра масс, отличающийся тем, что платформе сообщают одно реверсивно-симметричное сферическое вращение вокруг неподвижной точки, объединяющее систему вращений вокруг неподвижных осей, состоящее из реверсивно-симметричного прецессионного движения вокруг вертикальной оси и прямопропорциональное ему синхронное собственное вращение в угловом интервале [0-600°] при двух значениях коэффициента пропорциональности, обеспечивающих последовательные совпадения мгновенной оси вращения с шестью осями вертикального икосаэдра, принятые в качестве осей вращения тела.
2. Устройство для определения тензора инерции тела и центра масс тела, содержащее платформу в форме внешней рамки с валом, установленным в неподвижной подшипниковой опоре, внутренний вал с захватом для закрепления тела, установленным на платформе с возможностью его поворота, датчик угла поворота и угловой скорости платформы, автоматизированный электропривод в виде электродвигателя и зубчатого передаточного механизма, отличающееся тем, что вал внешней рамки жестко соединен с ротором двигателя, внутренний вал с захватом снабжен рамкой с цилиндрическим кожухом, передаточный механизм с вала двигателя на внутренний вал выполнен в виде пары цилиндрических колес и фрикционной электромуфты с двумя коническими колесами с возможностью поочередной фиксации их на валу муфты, зацепленные за неподвижные конические колеса.
РИСУНКИ
|
|