|
|
(21), (22) Заявка: 2007142793/06, 21.11.2007
(24) Дата начала отсчета срока действия патента:
21.11.2007
(46) Опубликовано: 20.02.2009
(56) Список документов, цитированных в отчете о
поиске:
RU 2215267 C2, 27.10.2003. RU 2049929 С1, 10.12.1995. US 5747703 А, 05.05.1998. SU 329392 А1, 09.02.1972. JP 2004333260 А, 25.11.2004.
Адрес для переписки:
111250, Москва, ул. Авиамоторная, 53, ЗАО “Патентный Поверенный”, пат.пов. Г.Н.Андрущак, рег. № 189
|
(72) Автор(ы):
Пилюзин Александр Васильевич (RU),
Клабуков Вилорий Михайлович (RU),
Помазуева Ириада Павловна (RU)
(73) Патентообладатель(и):
Общество с ограниченной ответственностью “Энергопромприбор” (RU)
|
(54) СПОСОБ ОПРЕДЕЛЕНИЯ ОБЪЕМНОГО РАСХОДА ЖИДКОСТИ В ТРУБОПРОВОДАХ ГИДРОЭЛЕКТРОСТАНЦИЙ (ВАРИАНТЫ)
(57) Реферат:
Изобретение относится к области гидроэнергетики, а именно к способам определения расходов жидкости в трубопроводах больших диаметров гидроэлектростанций при числах Рейнольдса Re>>lxl06. Первый способ заключается в определении локальных величин скоростей потока по радиусам поперечного сечения трубопровода. Поперечное сечение трубопровода разбивают на 3-8 кольцевых сегментов равных объемов при их основаниях. Затем определяют площади их оснований и вычисляют координату x° точек измерения относительно центра сечения трубопровода на основе степенного закона Никурадзе. В точках x° устанавливают гидрометрические вертушки, измеряют среднюю скорость потока в каждом сегменте и рассчитывают полный расход. Согласно второму способу излучают по хорде поперечного сечения трубопровода ультразвуковой импульс под острым углом « » к направлению движения потока. Затем измеряют время его прохождения в прямом и обратном направлениях и определяют среднюю скорость потока на хорде потока. На основе степенного закона Никурадзе получают функцию распределения средних величин скоростей по хордам и определяют весовые коэффициенты. Сумму весовых коэффициентов устанавливают, равной единице. Измеряют среднюю скорость потока по соответствующим хордам и вычисляют расход жидкости. Изобретение позволяет повысить точность измерений на величину до 10%. 2 н.п. ф-лы, 12 ил, 14 табл. » к направлению движения потока. Затем измеряют время его прохождения в прямом и обратном направлениях и определяют среднюю скорость потока на хорде потока. На основе степенного закона Никурадзе получают функцию распределения средних величин скоростей по хордам и определяют весовые коэффициенты. Сумму весовых коэффициентов устанавливают, равной единице. Измеряют среднюю скорость потока по соответствующим хордам и вычисляют расход жидкости. Изобретение позволяет повысить точность измерений на величину до 10%. 2 н.п. ф-лы, 12 ил, 14 табл.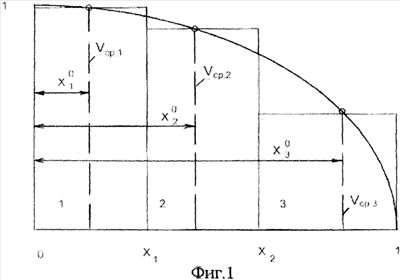
Изобретение относится к области гидроэнергетики, а именно к способам определения расходов жидкости в трубопроводах больших диаметров гидроэлектростанций при числах Рейнольдса Re>1×106.
Известен способ определения объемного расхода жидкости в трубопроводах гидравлических установок, заключающийся в определении локальных величин скоростей потока по радиусам поперечного сечения трубопровода, рекомендованный международным стандартом (ISO 3354, второе издание, 1968-07-015, Измерение расхода чистой воды в закрытых водоводах, Метод «скорость-площадь», основанный на применении гидрометрических вертушек в условиях заполненного водовода и достаточно равномерного течения/Международный стандарт ISO 3354, второе издание, 1968-07-015, Измерение расхода чистой воды в закрытых водоводах, Метод «скорость-площадь», основанный на применении гидрометрических вертушек в условиях заполненного водовода и достаточно равномерного течения/). Общие принципы этого способа следующие:
– измерительное сечение по радиусу разделяется на небольшое число элементов;
– распределение скоростей для каждого элемента подчиняется логарифмическому закону в виде:
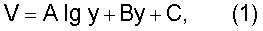
где А, В и С – какие-либо постоянные;
у – расстояние от стенки трубопровода;
– различные кривые, соответствующие каждому элементу сечения, не обязательно составляют непрерывную кривую с непрерывной производной;
– элементы сечения имеют площади, пропорциональные количеству измерительных точек в рассматриваемом элементе.
Основными недостатками известного способа являются:
– допущение разрывов функции распределения скоростей по радиусу на стыках элементов;
– элементы сечения по радиусу не должны иметь площади, пропорциональные количеству измерительных точек в рассматриваемом элементе, а каждому элементу должна соответствовать только одна измерительная точка;
– логарифмический закон распределения скоростей по радиусу (1) не имеет решения при у=0.
Известен способ определения объемного расхода жидкости в трубопроводах гидравлических установок при больших числах Рейнольдса Re>>106, заключающийся в излучении акустическим преобразователем по хорде поперечного сечения трубопровода ультразвукового импульса под острым углом « » к направлению движения потока, измерении времени прохождения ультразвукового импульса в прямом ti и обратном t2 направлениях и определение средней скорости потока на хорде потока по формуле: » к направлению движения потока, измерении времени прохождения ультразвукового импульса в прямом ti и обратном t2 направлениях и определение средней скорости потока на хорде потока по формуле:
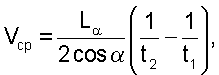
где L – длина акустического луча, – длина акустического луча,
включенный в международные нормы (International Standard, CEI/IES 41:1991 /2/). Согласно этому способу в случае круглого сечения трубопровода с акустическими лучами по хордам, расположенным точно на заданном расстоянии от центра, определяют расход в виде:
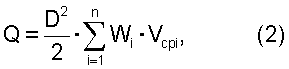
где n – число акустических лучей в одной плоскости;
D – диаметр трубопровода;
Vср.i – средняя величина скорости в створе акустического луча;
Wi – весовой коэффициент.
Недостатком известного способа является большая погрешность в определении объемного расхода жидкости.
Задачей изобретения является устранение указанных недостатков.
Техническим результатом, достигаемым при реализации изобретения, является повышение точности измерения объемного расхода жидкости, при этом решается задача размещения точек измерений локальных величин скоростей по радиусу с предельной точностью.
Поставленная задача решается, а технический результат достигается тем, что при определении объемного расхода жидкости в трубопроводах гидравлических установок по первому способу при больших числах Рейнольдса Re>>106, заключающемся в определении локальных величин скоростей потока по радиусам поперечного сечения трубопровода, поперечное сечение трубопровода разбивают на 3-8 кольцевых сегмента равных объемов при их основаниях с внутренним радиусом Xi и наружным Xi+1, определяют площади оснований сегментов, вычисляют координату х° точек измерения относительно центра сечения трубопровода из уравнений, основанных на степенном законе Никурадзе:
lnVср/0.1=ln(1-x°), где
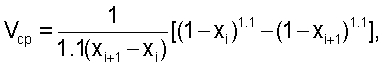
и устанавливают в точках х° гидрометрические вертушки, с помощью которых измеряют среднюю скорость потока в каждом сегменте и рассчитывают полный расход в соответствии с уравнением
Q= Vср.рFp, где Vср.рFp, где
p – номер кольцевого сегмента,
Vcp.р – средняя скорость в кольцевом сегменте,
Fp – площадь основания кольцевого сегмента.
Поставленная задача решается, а технический результат достигается тем, что при определении объемного расхода жидкости в трубопроводах гидравлических установок по второму способу при больших числах Рейнольдса Re>>106, заключающемся в излучении акустическим преобразователем по хорде поперечного сечения трубопровода ультразвукового импульса под острым углом « » к направлению движения потока, измерении времени прохождения ультразвукового импульса в прямом t1 и обратном t2 направлениях и определение средней скорости потока на хорде потока по формуле: » к направлению движения потока, измерении времени прохождения ультразвукового импульса в прямом t1 и обратном t2 направлениях и определение средней скорости потока на хорде потока по формуле:
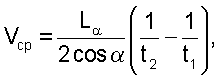
где L – длина акустического луча, – длина акустического луча,
на основе степенного закона Никурадзе в виде
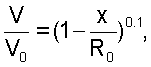
где V0 – максимальная величина скорости,
R0 – радиус сечения трубопровода,
х – расстояние от центра сечения трубопровода,
получают функцию распределения средних величин скоростей по хордам
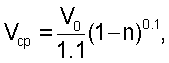
где n – расстояние от центра до хорды,
определяют весовые коэффициенты W из уравнения:
W(1-n)0.1/1.1=Vср,
при этом устанавливают сумму весовых коэффициентов равной единице, измеряют среднюю скорость потока по соответствующим хордам Vcpi и вычисляют расход жидкости по формуле:
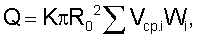
где i – номер хорды на половине сечения трубопровода,
К – коэффициент коррекции, установленный экспериментально и равный 1,047619.
В таблице 1 приведены параметры трубопроводов характерных гидравлических установок и их гидромеханические характеристики.
В таблице 2 дается сравнение расположений точек измерений на радиусе по международному стандарту и по заявленному способу.
В таблицах 3-8 приведены вычисления в безразмерных координатах параметров и характеристик по заявленному способу для трех, четырех и пяти сегментов.
В таблице 9 приведены вычисления величин расхода по уравнению, рекомендованному международным стандартом /2/ для диаметра трубопровода D=2 м (Vo=1) и их сравнение со значением, вычисленным по заявленному способу.
В таблице 10 приведены квадратурные правила Гаусса и Чебышева.
В таблице 11 показаны вычисленные величины расходов по квадратурным правилам Гаусса и Чебышева.
В таблице 12 приведены значения расстояний хорды от центра и весовых коэффициентов для схемы размещения в сечении трубопровода двух хорд.
В таблице 13 – результаты расчетов весовых коэффициентов со средней по сечению трубопровода скоростью по заявленному способу.
В таблице 14 приведены примеры длин отсеков трубопровода и соответствующих углов трассировки акустических лучей.
На фиг.1 показана схема разбивки эпюры скоростей на три кольцевых сегмента.
На фиг.2 – сечение трубопровода диаметром D=7 м с выбранными диаметрами D1 и D2.
На фиг.3 – эпюра скоростей, полученная при испытаниях на Братской ГЭС в случае размещения гидрометрической вертушки в центре сечения трубопровода.
На фиг.4 изображена схема метода прямого измерения времени распространения ультразвукового импульса от одного пьезопреобразователя к другому и обратно.
На фиг.5 приведена схема представления интеграла для определения средних величин скоростей по хордам.
На фиг.6 – функция распределения средних величин скоростей по хордам от центра до стенки трубопровода, при Vo=1.
На фиг.7 изображено сечение трубопровода с выбранной хордой, совпадающей с диаметром.
На фиг.8 приведена схема представления интеграла для определения средних величин скоростей по хорде, совпадающей с диаметром.
На фиг.9 изображено сечение трубопровода с выбранными двумя хордами.
На фиг.10 приведена схема представления интеграла для определения средних величин скоростей по двум хордам.
На фиг.11 изображено сечение трубопровода с выбранными четырьмя хордами.
На фиг.12 приведена схема представления интеграла для определения средних величин скоростей по четырем хордам.
Предлагаемые способы базируются на использовании экспериментальных данных и направлены на повышение точности измерения расходов с применением технических средств измерений локальных величин скоростей (точечные измерения) или интегральных величин (акустические методы).
Распределение скоростей по сечению трубопровода зависит от числа Рейнольдса (Re), т.е. от степени турбулентности потока. Однако при очень больших числах Рейнольдса (Re>>1×106) такая зависимость практически исчезает и закон распределения скоростей по сечению трубопровода становится универсальным – предельным (Nikuradse J, Uber turbulente Wasserstormungen in geraden Rohren bei sehr Grossen Reynoldschen Zahlen? Aachener Vortrage, 1930 /3/; Г.Шлихтинг. Теория пограничного слоя. М.: Наука, 1969 /4/).
Вычисление числа Рейнольдса производится по известному выражению:
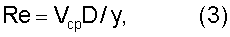
где y – коэффициент кинематической вязкости воды, принятый равным 1,1401×10-6 м/с при температуре воды +15°С и атмосферном давлении – среднее значение (Александров А.А., Трахтенгерц М.С. Теплофизические свойства воды при атмосферном давлении, изд-во стандартов, 1977 /5/).
Максимальные величины числа Рейнольдса для турбинных режимов определяют для расчетных напоров, а минимальные – по расходам холостого хода, что составляет примерно 0,175 от номинального расхода (Кривченко Г.И. Гидравлические машины. М.: Энергия, 1976 /6/).
Данные таблицы 1 дают полное представление о том, что в трубопроводах гидравлических установок (ГЭС, ГАЭС и насосных станций) движение потока характеризуется очень большими числами Рейнольдса. При этих условиях может быть использован эмпирический степенной закон распределения величин скорости “V” по радиусу J. Nicuradse /3, 4/ в виде:
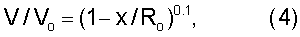
где Vо – максимальная величина скорости;
Ro – радиус сечения трубопровода;
x – расстояние от центра сечения трубопровода.
Показатель степени, равный 0.1, считается предельным, поскольку существуют асимптотические законы, содержащие логарифм, как предельное значение очень малой степени /4/. С физической точки зрения эти асимптотические законы характерны наличием только турбулентного течения, т.к. при больших числах Рейнольдса ламинарное течение полностью отходит на задний план по сравнению с турбулентным.
Предлагаемые разработки способов определения величин расхода в трубопроводах базируется на использовании уравнения (4).
Способ определения объемного расхода жидкости в трубопроводах гидравлических установок при больших числах Рейнольдса Re>>106, заключается в определении локальных величин скоростей потока по радиусам поперечного сечения трубопровода. Согласно изобретению поперечное сечение трубопровода разбивают на 3-8 кольцевых сегмента с внутренним радиусом xi и наружным xi+1, определяют площади оснований сегментов, вычисляют координату х° точек измерения относительно центра сечения трубопровода из уравнений, основанных на степенном законе Никурадзе в форме:
lnVср/0.1=ln(1-x°), где
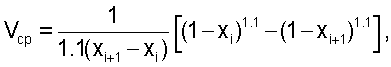
и устанавливают в точках x° гидрометрические вертушки, с помощью которых измеряют среднюю скорость потока в каждом сегменте и рассчитывают полный расход в соответствии с уравнением
Q= Vcp.pFp, где Vcp.pFp, где
р – номер кольцевого сегмента,
Vcp.p – средняя скорость в кольцевом сегменте,
Fp – площадь основания кольцевого сегмента.
Указанные уравнения были получены следующим образом.
Предлагаемый способ, базирующийся на использовании экспериментально обоснованного степенного закона распределения величин скоростей по радиусу (4), позволяет решить задачу размещения точек измерений локальных величин скоростей по радиусу с предельной точностью.
Применяя степенной закон распределения скоростей по радиусу трубопровода (4), запишем:
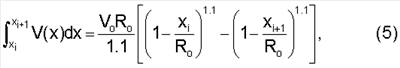
где i=0, 1, 2 и т.д.
Интеграл (5) выражает площадь поперечного сечения того или иного сегмента.
Решая задачу в безразмерных координатах, т.е. приняв Vo=1 и Ro=1, имеем:
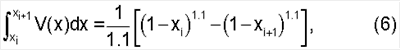
поделив интеграл (6) на ширину сегмента (xi+1-xi), получим среднюю величину скорости «Vcp» для каждого из сегментов:
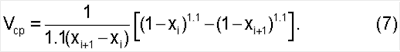
Умножив величину «Vcp» на площадь поперечного сечения кольцевого сегмента, получим величину расхода, проходящего через этот сегмент:
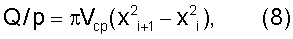
где p – число сегментов (расходы через все сегменты равны).
Расход Q, а иначе объем тела вращения с образующей по уравнению (4) равен:
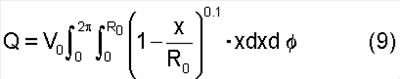
Уравнение (9) после вычисления интеграла приобретает вид:
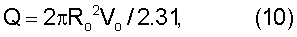
или, при Ro=1 и Vo=1, Q=2,71999, а площадь сечения F= =3.141593. =3.141593.
Расстояния от центра до точек измерений «х°» на фиг.1 определяется по уравнению:
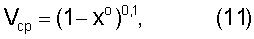
которое для вычислений преобразуется в вид:
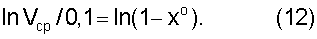
Столь значительное расхождение расположений точек измерений на радиусе по международному стандарту и по заявленному способу (таблица 2) связано, в основном, допущением в международном стандарте разрывов функции распределения скоростей по радиусу.
Вычисленные по заявленному способу параметры и характеристики для трех, четырех и пяти сегментов в безразмерных координатах представлены в таблицах 3-8.
Величина расхода для реальных условий определяется по выражению:
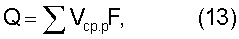
где р – номер сегмента;
Vcp.р – средняя скорость в сегменте;
F – площадь основания сегмента.
Центральную область ядра течения не следует загружать измерительными средствами, т.к. это может привести к искажению функции распределения скоростей по сечению. Так, при испытаниях на Братской ГЭС из-за размещения гидрометрической вертушки в центре сечения трубопровода наблюдалось значительное искажение эпюры скоростей (фиг.3).
Другой вариант способа определения объемного расхода жидкости в трубопроводах гидравлических установок при больших числах Рейнольдса Re>>106 заключается в излучении акустическим преобразователем по хорде поперечного сечения трубопровода ультразвукового импульса под острым углом « » к направлению движения потока, измерении времени прохождения ультразвукового импульса в прямом t1 и обратном t2 направлениях и определение средней скорости потока на хорде потока по формуле: » к направлению движения потока, измерении времени прохождения ультразвукового импульса в прямом t1 и обратном t2 направлениях и определение средней скорости потока на хорде потока по формуле:
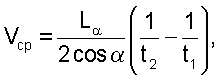
где L – длина акустического луча, – длина акустического луча,
Согласно изобретению на основе степенного закона Никурадзе в виде
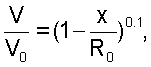
где V0 – максимальная величина скорости,
R0 – радиус сечения трубопровода,
x – расстояние от центра сечения трубопровода,
получают функцию распределения средних величин скоростей по хордам
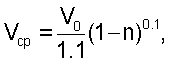
где n – расстояние от центра до хорды,
определяют весовые коэффициенты W из уравнения:
W(1-n)0.1/1.1=Vср,
при этом устанавливают сумму весовых коэффициентов равной единице, измеряют среднюю скорость потока по соответствующим хордам Vcpi и вычисляют расход жидкости по формуле:
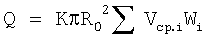 , ,
где i – номер хорды на половине сечения трубопровода,
К – коэффициент коррекции, равный 1,047619.
Указанные уравнения были получены следующим образом.
Акустический способ использует метод прямого измерения времени распространения каждого индивидуального ультразвукового импульса от одного пьезопреобразователя к другому (t1) и обратно (t2) (фиг.4-5). По измеренным величинам “t1” и “t2” вычисляется средняя осевая скорость в створе акустического луча в виде:
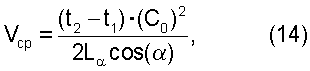
где
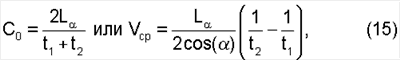
После определения средней скорости по сечению трубопровода (Vcp.F) величина расхода определяется по выражению:
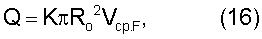
где Ro – радиус трубопровода,
К – коэффициент коррекции, учитывающий схему размещения акустических лучей в сечении трубопровода (k<1, если измерения выполняются через центр трубопровода и k>1, если измерения выполнялись по хордам).
По обозначениям схемы представления интеграла для определения средних величин скоростей по хордам на фиг.5 имеем:
x=nRo/cos , откуда dx=nRo d(sc , откуда dx=nRo d(sc ) )
или dx=nRo(sin /cos2 /cos2 )d )d . .
Подставляя эти величины в интеграл от функции V(x) (уравнение 4), получим:
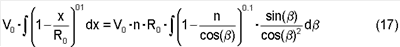
Для разрешения интеграла (17) используем подстановку cos  =1/t, производная от которой равна sin =1/t, производная от которой равна sin d d =(1/t2)dt. =(1/t2)dt.
Интеграл после замены переменной примет вид:
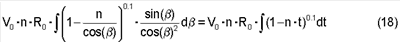
Интеграл (18) при пределах интегрирования от t1=1/cos (0) до t2=1/n будет равен:
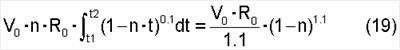
Этот интеграл определен для участка Ro(l-n).
Средняя скорость на этом участке равна:
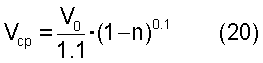
Такая же средняя величина скорости будет и по хорде (автомодельность функции распределения скоростей на участке Ro(l-n) и на хорде).
На фиг.6 кривой 2 обозначена функция распределения средних величин скоростей по хордам от центра до Ro=1 при Vo=1.
Средняя скорость по сечению трубопровода, определенная по хордам при Vo=1, равна:
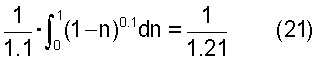
т.е. средняя скорость по площади сечения трубопровода Vср.F=0.826446.
Выявить причины столь внушительных погрешностей вычисления величин расхода по уравнению, рекомендованному международным стандартом 121 для диаметра трубопровода D=2 м (Vo=1) по сравнению со значением, вычисленным по заявленному способу (таблица 9), не представляется возможным, поскольку не приводится способ преобразования классической формы представления величины расхода (произведение площади сечения трубопровода на среднюю скорость в сечении) в формулу вида (2).
Помимо указанного ошибочны и другие рекомендации международного стандарта /2/.
Так, например, утверждается наличие радиальных составляющих скорости.
Поскольку стенки трубопровода не проницаемы, такое явление исключается. Радиальные составляющие имеют место в водоводах переменного сечения (диффузоры, конфузоры), но они взаимно исключаются.
Приведенная в международном стандарте /2/ схема размещения акустических лучей в одной плоскости (например, четыре луча) нарушает канонический принцип гидромеханики. В гидромеханике для изучения характера потока рассматривается отсек трубопровода, ограниченный двумя плоскостями, перпендикулярными к оси водовода. Это является необходимым для оценки краевых условий (постоянство всех параметров потока в поперечном сечении) и условий неразрывности.
Предлагаемые решения не только устраняют указанные недостатки, но и обосновывают точные способы определения величины расхода при применении ультразвуковых расходомеров.
На фиг.6 кривая «1», построенная по уравнению (2) при Ro=1 и Vo=1, обозначает распределение скоростей по радиусу.
Средняя скорость будет равна:
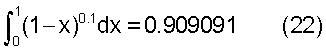
Средняя скорость по сечению трубопровода по уравнению (9) равна:
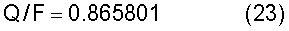
Отсюда, для определения расхода при измерениях по диаметру (фиг.7-8) вводится коэффициент коррекции К=0,952381 (0,865801/0,909091).
Кривая «2» на фиг.6, обозначающая функцию распределения средних скоростей по хордам, характеризуется средней величиной по радиусу, равной Vcp=0.826446 (уравнение 21). Поэтому коэффициент коррекции по хордам отличается от радиального и равен К=1,047620 (0,9090910/00,826446).
Коэффициент коррекции «К» в зависимости от схемы измерений вводится в уравнение (16).
В международном стандарте 121 используются квадратурные правила Гаусса в предположении, что функция распределения скоростей по сечению не известна.
В таблице 10 приведены некоторые квадратурные правила Гаусса и Чебышева для  f(n) dn с пределами от (-1) до (+1), где n – часть единичного радиуса. f(n) dn с пределами от (-1) до (+1), где n – часть единичного радиуса.
Вычисления расходов по квадратурным правилам таблицы 10 выполнялись в относительных единицах (Ro=1 и Vo=1) по уравнению:
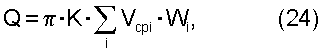
где К=1,047619 – коэффициент коррекции;
Vcp.i – (1-ni)0.1 1,1 – средняя скорость для i – того узла;
Wi – весовой коэффициент для i -того узла;
i – число узлов на половине поперечного сечения трубопровода.
Результаты расчетов, приведенные в таблице 11, показывают, что действительная функция распределения скоростей по сечению трубопровода не достаточно гладкая, что приводит к завышению величин расходов при использовании известных квадратурных правил.
Также подтверждается ошибочность рекомендаций международного стандарта /2/, не учитывающих необходимость введения коэффициента коррекции, согласовывающего величину средней скорости по хордам со средней скоростью по сечению трубопровода.
Поскольку известна экспериментально обоснованная функция распределения скоростей по сечению трубопровода (уравнение 4), а по ней определена зависимость средних величин скоростей по хордам (кривая 2, фиг.6), то можно обосновать точные квадратурные правила.
Можно распорядиться выбором весовых коэффициентов «W» и расположением хорд от оси /7/ и подчинить этот выбор требованию быть точными для зависимости средних величин скоростей по хордам (кривая 2, фиг.6).
Второе требование, обычное для квадратурных правил, заключается в том, что сумма весовых коэффициентов для числа узлов более двух (4, 6, 8 и т.д.) должна быть равна единице.
Третье требование – расстояния хорд от центра не должны быть иррациональными, чтобы упростить и сделать точным процесс разбивки створов размещения акустических лучей.
Четвертое требование – размещение акустических лучей должно выполняться в отсеках, ограниченных двумя плоскостями, перпендикулярными к оси трубопровода (сохранение канонов гидромеханики).
В таблице 12 приведены значения расстояний хорды от центра и весовых коэффициентов для схемы размещения в сечении трубопровода двух хорд (фиг.9-10).
Вычисления весовых коэффициентов “W ” при заданных величинах “n” выполнены по уравнению в виде:
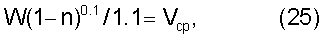
где W – весовой коэффициент;
Vcp=0,826446 – средняя осевая скорость при изменении “n” от 0 до 1 (кривая 2, фиг.6).
Для схемы измерения по четырем хордам (фиг.11-12) уравнение вычисления весовых коэффициентов имеет вид:
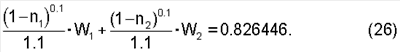
Используя равенство W1+W2=1, уравнение (26) примет вид:
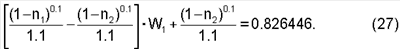
Результаты расчетов точных квадратурных правил для различных пар «n1» и «n2» приведены в таблице 13.
Достоинством таких квадратурных правил, помимо их точности, является отсутствие иррациональных величин расстояний хорд (узлов) от центра. Это упрощает разбивку и повышает точность трассировки акустических лучей.
В таблице 14 в качестве примеров приведены длины отсеков трубопровода (Lотс) и углы трассировки акустических лучей относительно горизонтальной плоскости, проходящей через ось трубопровода.
Для реальных условий могут быть подобраны и другие пары расстояний узлов от центра (n1, n2) а также длины отсеков «Lотс», но при этом желательно, чтобы угол  ° оставался в пределах 45°±10°. Угол ° оставался в пределах 45°±10°. Угол  °=45° считается, обычно, оптимальным. °=45° считается, обычно, оптимальным.
Анализ, выполненный выше, производился в безразмерных координатах при Ro и Vo равных единице.
Для реальных условий расход определяется по следующим уравнениям:
Случай двух хорд (фиг.9-10)
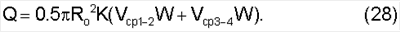
Случай четырех хорд (фиг.11-12)
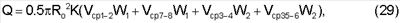
где Ro – радиус трубопровода, м;
К=1,047619 – безразмерный коэффициент коррекции, учитывающий, что средняя скорость, определенная по хордам, меньше средней скорости по сечению трубопровода;
Vcp – средние скорости по хордам, определенные уравнениями (14) или (15) по измеренным параметрам «t1» и «t2», м/с;
W – безразмерные весовые коэффициенты.
Определение объемов расхода жидкости в трубопроводах гидравлических установок при больших числах Рейнольдса Re>>106 по заявленным способам позволяет повысить точность определения величины объемного расхода жидкости.
Источники информации
1. Международный стандарт ISO 3354, второе издание, 1968-07-015. Измерение расхода чистой воды в закрытых водоводах. Метод «скорость-площадь», основанный на применении гидрометрических вертушек в условиях заполненного водовода и достаточно равномерного течения.
2. INTERNATIONAL STANDARD, CEI/IES 41:1991.
3. Nikuralse J, Uber turbulente Wasserstromungen in geraden Rohren bei sehr Grossen Reynoldschen Zahlen, Aachener Vortrage, 1930.
4. Г.Шлихтинг. Теория пограничного слоя. М.: Наука, 1969.
5. Александров А.А., Трахтенгерц М.С. Теплофизические свойства воды при атмосферном давлении, изд-во стандартов, 1977.
6. Кривченко Г.И., Гидравлические машины. М.: Энергия, 1976.
7. Кахонер Д., Маулер Л., Нэш С. Элементы численного анализа и математической обработки результатов опыта. М.: Наука, 1970.
| ТАБЛИЦА 1 |
| Объект |
Расход Q м/с |
Напор
Н м |
Диаметр водовода D м |
Средняя скорость Vср |
Re×106 |
| |
|
|
|
|
Макс. |
Мин. |
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
| Усть-Илимская ГЭС (Россия) |
315 |
85,5 |
7,8 |
6,6 |
45 |
8 |
| ГЭС Пурнари (Греция) |
168 |
66,5 |
7,0 |
4,4 |
27 |
5 |
| Байпазинская ГЭС (Таджикистан) |
285 |
56,9 |
7,6 |
6,3 |
42 |
7 |
| Братская ГЭС (Россия) |
290 |
103 |
7,0 |
7,5 |
46 |
8 |
| Нурекская ГЭС (Таджикистан) |
135 |
260 |
6,0 |
4,8 |
25 |
4 |
| Вилюйская ГЭС (Россия) |
152,5 |
65 |
6,0 |
5,4 |
28 |
5 |
| ГЭС Аль-Вахда (Морокко) |
144 |
68 |
5,7 |
5,6 |
28 |
5 |
| Курская АЭС Насосная станция подпитки (Россия) |
4 |
10 |
1,2 |
3,5 |
4 |
2 |
| Загорская ГАЭС (Россия), турбинный режим |
226 |
100 |
7,5 |
5,1 |
33 |
6 |
| То же, насосный |
205 |
96 |
7,5 |
4,6 |
30 |
– |
| режим |
170 |
114,5 |
7,5 |
3,8 |
|
25 |
| ТАБЛИЦА 2 |
| Количество точек измерений на радиусе |
X/Ro |
| |
Стандарт ISO 33-54 (1988-07-015) |
По предлагаемой методике |
Расхождение в% от Ro=1 |
| |
0,3686 |
0,2891 |
8 |
| 3 |
0,7302 |
0,6742 |
6 |
| |
0,9358 |
0,9336 |
0,2 |
| |
0,2776 |
0,2192 |
6 |
| |
0,5858 |
0,5147 |
7 |
| 5 |
0,6950 |
0,6773 |
2 |
| |
0,8470 |
0,8131 |
3 |
| |
0,9622 |
0,9579 |
0,4 |
| ДЛЯ ТРЕХ СЕГМЕНТОВ |
| ТАБЛИЦА 3 |
№№
сегмента |
Средняя
скорость |
Площадь
основания
сегмента |
Расход |
| |
Vср |
VcpF |
| |
|
F |
|
| 1 |
0,966450 |
0,938139 |
0,90666 |
| 2 |
0,893917 |
1,014258 |
0,90666 |
| 3 |
0,762414 |
1,189196 |
0,90666 |
| Итого: |
|
3,141593 |
2,71998 |
| ТАБЛИЦА 4 |
№№
сегмента |
Расстояние
от центра до узла измерений x/Ro |
Размеры оснований сегментов |
| Хнач. |
Хкон. |
Хкон.-Хнач. |
| 1 |
0,289124 |
0 |
0,546460 |
0,546460 |
| 2 |
0,674184 |
0,546460 |
0,788332 |
0,241872 |
| 3 |
0,933640 |
0,788332 |
1 |
0,211668 |
| Итого: |
|
|
|
1,000000 |
| ДЛЯ ЧЕТЫРЕХ СЕГМЕНТОВ |
| ТАБЛИЦА 5 |
№№
сегмента |
Средняя
скорость
Vср |
Площадь
основания
сегмента
F |
Расход
VcpF |
| 1 |
0,972016 |
0,699574 |
0,679997 |
| 2 |
0,917270 |
0,741327 |
0679997 |
| 3 |
0,865592 |
0,785587 |
0,679998 |
| 4 |
0,743082 |
0,915105 |
0,679998 |
| Итого: |
|
3,141593 |
2,71999 |
| ТАБЛИЦА 6 |
№№
сегмента |
Расстояние
от центра до узла измерений x/Ro |
Размеры оснований сегментов |
| Хнач. |
Хкон. |
Хкон.-Хнач. |
| 1 |
0,247105 |
0 |
0,471891 |
0,471891 |
| 2 |
0,578331 |
0,471891 |
0,677239 |
0,205348 |
| 3 |
0,763880 |
0,677239 |
0,841851 |
0,164612 |
| 4 |
0,948670 |
0,841851 |
1 |
0,158149 |
| Итого: |
|
|
|
1,000000 |
| ДЛЯ ПЯТИ СЕГМЕНТОВ |
| ТАБЛИЦА 7 |
| №№ |
Средняя |
Расстояние |
Площадь |
Расход |
| сегмента |
скорость |
от центра до |
основания |
VcpF |
| |
Vcp |
узла измерений |
сегмента |
|
| |
|
x/Ro |
F |
|
| 1 |
0,975558 |
0,219216 |
0,557629 |
0,54400 |
| 2 |
0,930253 |
0,514699 |
0,584789 |
0,54400 |
| 3 |
0,893065 |
0,677276 |
0,609130 |
0,54399 |
| 4 |
0,845585 |
0,813116 |
0,643343 |
0,54400 |
| 5 |
0,728538 |
0,957877 |
0,746701 |
0,54400 |
| Итого: |
|
|
3,141593 |
2,71999 |
| ТАБЛИЦА 8 |
№№
сегмента |
Размеры оснований сегментов |
| Хнач. |
Хкон. |
Хкон.-Хнач. |
| 1 |
0 |
0,421306 |
0,421306 |
| 2 |
0,421306 |
0,603028 |
0,181722 |
| 3 |
0,603028 |
0,746683 |
0,143655 |
| 4 |
0,746683 |
0,873108 |
0,126425 |
| 5 |
0,873108 |
1 |
0,126892 |
| Итого: |
|
|
1,000000 |
| ТАБЛИЦА 9 |
| Наименование |
Метод Гаусса-Лежандра |
Метод Гаусса-Якоби |
| Расстояние от центр |
±0,861136 |
±0,809017 |
| до хорды |
±0,39981 |
±0,309017 |
| Средняя величина |
0,746219 |
0,770383 |
| Скорости, Vcp.i |
0,863921 |
0,876101 |
| Весовой |
0,176841 |
0,217079 |
| коэффициент, Wi |
0,613299 |
0,568320 |
| 2Vcp/iWi |
0,263924 |
0,334468 |
| |
1,059559 |
0,995812 |
Q=2 Vcp.iWi Vcp.iWi |
2,646966 |
2,660559 |
| Погрешность |
-2,7 |
-2,2 |
| ТАБЛИЦА 10 |
Автор,
источник |
Число
узлов |
ni
расстояние
хорды от
центра |
Wi
Вес |
| Гаусс-Лежандр |
2 |
±0,577350269 |
1 |
| Гаусс-Лежандр |
4 |
±0,861136312 |
0,347854845 |
| |
|
±0,339981044 |
0,652145155 |
| Гаусс-Лежандр |
8 |
±0,960289956 |
0,101228536 |
| |
|
±0,796666477 |
0,222381034 |
| |
|
±0,525532410 |
0,313706646 |
| |
|
±0,183434642 |
0,362683787 |
| Чебышев |
4 |
±0,211325 |
0,5 |
| |
|
±0,788675 |
|
| Чебышев |
8 |
±0,102637 |
0,25 |
| |
|
±0,406204 |
|
| |
|
±0,593796 |
|
| |
|
±0,897327 |
|
| ТАБЛИЦА 11 |
| Автор квадратурных правил |
Общее число узлов |
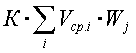 |
Расход по уравнению (24) |
Ошибка в % |
| Точная величина расхода по |
– |
|
2,719974 |
|
| Гаусс-Лежандр |
2 |
0,873793 |
2,745103 |
+0,9 |
| Гаусс-Лежандр |
4 |
0,867750 |
2,726118 |
+0,22 |
| Гаусс-Лежандр |
8 |
0,866216 |
2,721297 |
+0,05 |
| Чебышев |
4 |
0,872660 |
2,741543 |
+0,79 |
| Чебышев |
8 |
0,868741 |
2,729231 |
+0,34 |
| ТАБЛИЦА 12 |
| Расстояние хорды от центра |
Значение функции (l-n)0.1/l.1 |
Весовой коэффициент W |
Средняя скорость на участке от n=0 до n=1 |
| 0.2 |
0.889030 |
0.929604 |
0.826446 |
| 0.4 |
0.863818 |
0.956736 |
0.826446 |
| 0.6 |
0.829494 |
0.996325 |
0.826446 |
| ТАБЛИЦА 13 |
№№
п.п. |
Число
узлов
(хорд) |
Расстояние
узлов
от центра,
n |
(1-n)0.1/1.1 |
Весовой
коэффициент
W |
Средняя
скорость
по сечению
водовода |
| 1 |
4 |
±0,2 |
0,889030 |
0,246511 |
|
| |
|
±0,7 |
0,805971 |
0,753488 |
0,826446 |
| 2 |
4 |
±0,3 |
0,887237 |
0,463413 |
|
| |
|
±0,8 |
0,773945 |
0,536587 |
0,826446 |
| 3 |
4 |
±0,25 |
0,883311 |
0,566951 |
|
| |
|
±0,85 |
0,751998 |
0,433049 |
0,826446 |
| ТАБЛИЦА 14 |
Число
лучей
хорд |
Расстояние
от центра
n |
Длина
отсека
Lотс |
Угол трассировки
акустического луча
в градусах (фиг.5) |
| 1 |
2 |
3 |
4 |
| 2 |
|
|
|
| (в одной плоскости) |
±0,25 |
1,94 |
45 |
| 1 |
2 |
3 |
4 |
| 2 |
|
|
|
| (в одной плоскости) |
±0,50 |
1,73 |
45 |
| 4 |
|
|
|
| (в двух |
±0,2 |
1,69 |
 1=49,16 1=49,16 |
| плоскостях) |
±0,7 |
|
 2=40,14 2=40,14 |
| 4 |
|
|
|
| (в двух |
±0,3 |
1,56 |
 1=50,84 1=50,84 |
| плоскостях) |
±0,8 |
|
 2=37,68 2=37,68 |
| 4 |
|
|
|
| (в двух |
±0,25 |
1,495 |
 1=52,33 1=52,33 |
| плоскостях) |
±0,85 |
|
 2=35,17 2=35,17 |
Формула изобретения
1. Способ определения объемного расхода жидкости в трубопроводах гидравлических установок при больших числах Рейнольдса Re>>106, заключающийся в определении локальных величин скоростей потока по радиусам поперечного сечения трубопровода, отличающийся тем, что поперечное сечение трубопровода разбивают на 3-8 кольцевых сегментов, равных объемов при их основании с внутренним радиусом xi и наружным xi+1, определяют площади оснований сегментов, вычисляют координату x° точек измерения относительно центра сечения трубопровода из уравнений, основанных на степенном законе Никурадзе
lnVср/0,1=ln(1-x°),
где 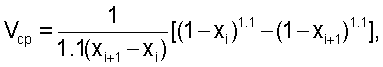
и устанавливают в точках x° гидрометрические вертушки, с помощью которых измеряют среднюю скорость потока в каждом сегменте и рассчитывают полный расход в соответствии с уравнением
Q= Vcp.pFp, Vcp.pFp,
где р – номер кольцевого сегмента;
Vcp.p – средняя скорость в кольцевом сегменте;
Fp – площадь основания кольцевого сегмента.
2. Способ определения объемного расхода жидкости в трубопроводах гидравлических установок при больших числах Рейнольдса Re>>106, заключающийся в излучении акустическим преобразователем по хорде поперечного сечения трубопровода ультразвукового импульса под острым углом « » к направлению движения потока, измерении времени прохождения ультразвукового импульса в прямом t1 и обратном t2 направлениях и определении средней скорости потока на хорде потока по формуле » к направлению движения потока, измерении времени прохождения ультразвукового импульса в прямом t1 и обратном t2 направлениях и определении средней скорости потока на хорде потока по формуле
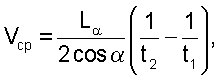
где L – длина акустического луча, отличающийся тем, что на основе степенного закона Никурадзе в виде – длина акустического луча, отличающийся тем, что на основе степенного закона Никурадзе в виде
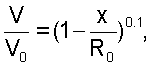
где Vo – максимальная величина скорости;
Ro – радиус сечения трубопровода;
x – расстояние от центра сечения трубопровода,
получают функцию распределения средних величин скоростей по хордам
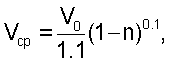
где n – расстояние от центра до хорды, определяют весовые коэффициенты W из уравнения
W(1-n)0.1/1.1=Vср,
при этом устанавливают сумму весовых коэффициентов, равной единице, измеряют среднюю скорость потока по соответствующим хордам Vсрi и вычисляют расход жидкости по формуле:
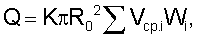
где i – номер хорды на половине сечения трубопровода;
К – коэффициент коррекции, равный 1,047619.
РИСУНКИ
|
|