Патент на изобретение №2342705
|
||||||||||||||||||||||||||
(54) КОМПЬЮТЕРНЫЙ СПОСОБ ФОРМИРОВАНИЯ ИЗОБРАЖЕНИЯ ЧАСТЕЙ ЛОМАНОЙ ЛИНИИ, ЛЕЖАЩИХ КАК ВНУТРИ, ТАК И ВНЕ МНОГОУГОЛЬНОЙ ОБЛАСТИ, И КОМПЬЮТЕРНЫЙ СПОСОБ ФОРМИРОВАНИЯ ИЗОБРАЖЕНИЯ ГРАНИЦ ОДНОЙ ИЛИ НЕСКОЛЬКИХ ОБЛАСТЕЙ, ПОЛУЧЕННЫХ В РЕЗУЛЬТАТЕ ПРИМЕНЕНИЯ ЗАДАННОЙ ЛОГИЧЕСКОЙ ОПЕРАЦИИ К ДВУМ МНОГОУГОЛЬНЫМ ОБЛАСТЯМ
(57) Реферат:
Изобретение относится к способам генерации двумерных векторных изображений путем комбинирования фигур, точнее к компьютерным способам формирования векторных изображений путем выполнения логических операций над ломаными линиями и многоугольными областями. Изобретение обеспечивает повышение надежности формирования изображений по сравнению с известными способами без использования вычислений с неограниченной разрядностью мантиссы. Решение поставленной задачи при выполнении операций над ломаной линией и областью достигается за счет нахождения пограничных отрезков ломаной линии, лежащих в
Изобретение относится к способам генерации двумерных векторных изображений путем комбинирования фигур, точнее к компьютерным способам формирования векторных изображений путем выполнения логических операций над ломаными линиями и многоугольными областями. Изобретение может быть использовано, например, для автоматизации редактирования и проверки картографической информации о линейных и площадных объектах в геоинформационных системах и земельно-информационных системах. В современных геоинформационных системах (ГИС) и земельно-информационных системах (ЗИС) актуальной является задача выполнения различных логических операций над объектами, представляющими собой векторные изображения материальных объектов в виде ломаных линий на плоскости (ниже – «ломаных линий») и областей на плоскости (ниже – «областей»). Для ломаной линии и области определены операции пересечения ломаной линии с областью и вычитания области из ломаной линии. Для областей определены операции объединения, пересечения и вычитания одной области из другой. Такие операции используются как при создании и проверке корректности топографических карт и планов, так и на этапе использования карт и планов в ГИС (ЗИС). Под пересечением ломаной линии с областью понимают часть или совокупность нескольких частей ломаной линии, лежащих внутри области. Под результатом вычитания области из ломаной линии понимают часть или совокупность нескольких частей ломаной линии, лежащих вне области. Пересечение ломаной линии с областью часто используется при создании электронных карт, например, при автоматической нарезке карты на листы. Вычитание области из ломаной линии используется, когда требуется обеспечить удаление частей линейных объектов, попадающих внутрь заданной области, например автоматически построенных горизонталей внутри площадных рек. При создании карт и планов часто требуется, чтобы получающиеся в результате оцифровки изображений области попарно не пересекались и в совокупности покрывали все пространство карты (плана). В этом случае обычно операторы оцифровывают границы мелких объектов (домов, дорог и т.п.), а области окружающих их земельных участков получают путем вычитания указанных мелких объектов из области всей прилегающей территории. Существенно, что при обработке стереоизображений, на которых оператор видит только крыши домов, но не видит полностью их основания, граница земельного участка с домом может быть получена только автоматически путем вычитания площади дома из области данного участка, поскольку реально полностью она не видна на стереоизображении. При проведении контроля корректности результатов оцифровки существенные усилия затрачиваются на проверку того, что различные примыкающие друг к другу земельные участки не пересекаются и в совокупности покрывают все пространство кадастрового квартала. Здесь необходим автоматический контроль правильности состыковки соседних областей на карте (плане). В случае обнаружения ошибок необходимо корректировать одну из этих областей, вычитая из нее пересечение этих двух областей или объединяя ее с областью, представляющей собой «оставшуюся лишней» часть карты (плана) между двумя областями. На этапе эксплуатации ГИС (ЗИС) выполнение логических операций над областями используется как при интеграции распределенных баз данных (создании единых векторных карт из нескольких тематических), так и при реализации запросов на выдачу геометрических свойств объектов и их сочетаний. Например, при объединении информации из топографических и из гидрографических карт (планов) необходимо получать границы тех частей земельных участков, которые соответственно заняты и не заняты объектами гидрографии (реками, прудами, озерами, болотами и т.п.). Это приводит к необходимости выполнения операций пересечения и вычитания площадных объектов. Из всего вышесказанного вытекает важность автоматического выполнения различных логических операций над ломаными и над многоугольными областями, являющимися векторными изображениями площадных объектов на плоскости. В [М. de Berg, M. van Kreveld, M.Overmars, O.Schwarzkoft. Computational Geometry. Algorithms and Applications. Springer-Verlag Berlin Heidelberg, 1997. pp.33-39] излагается способ определения частей ломаной линии, лежащих внутри и лежащих вне многоугольной области, заданной как набор контуров в виде многоугольников на плоскости, включающий в себя внешний контур и контуры дыр, в котором формируют части ломаных линий, лежащие внутри или вне указанной области, путем анализа взаимного расположения указанной ломаной линии и границ указанной области, используя вычисление координат точек пересечения ломаной линии и контуров границы области и определение взаимного расположения отрезков ломаной линии и отрезков границ области методом заметания плоскости. Недостатком этого способа является его низкая надежность в ситуациях, когда некоторые вершины ломаной линии расположены очень близко к границам области. В этом случае при определении точек пересечения получаются плохо обусловленные системы уравнений, что приводит к очень большим погрешностям при определении точек пересечения, а также к ошибкам в определении взаимной ориентации контуров и, как следствие, к неправильным результатам при определении тех частей ломаной линии, которые лежат внутри или вне области.
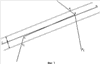
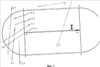
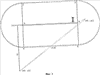
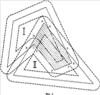
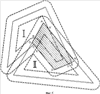
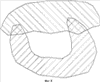
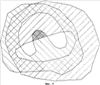
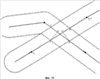
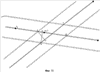
С учетом всего сказанного, актуальной является задача разработки надежного компьютерного способа формирования изображения частей ломаной линии, лежащих как внутри, так и вне многоугольной области, который имел бы высокую надежность, использовал бы обычную машинную арифметику и давал бы результат с ошибкой, не превышающей заданную точность Решение первой задачи достигается за счет формирования изображения частей ломаной линии, лежащих как внутри, так и вне многоугольной области, заданной как набор контуров в виде многоугольников на плоскости, включающий в себя внешний контур и контуры дыр, с заданной точностью – находят пограничные части упомянутой ломаной линии, лежащие в – подсчитывают, для каждой из упомянутых оставшихся частей, число пересечений луча, выходящего из любой точки данной оставшейся части, с границами упомянутой многоугольной области; – классифицируют упомянутые оставшиеся части на внутренние и внешние в зависимости от того, является ли результат упомянутого подсчета, соответственно, нечетным или четным. Наконец, выдают полученные в процессе упомянутой компьютерной обработки данные о пограничных, внутренних и (или) внешних частях упомянутой ломаной линии на устройство вывода данных упомянутого компьютера. При этом границы упомянутой области могут иметь самопересечения и самокасания, причем внутренностями областей считаются геометрические места точек, для которых какой-либо луч, выходящий из данной точки, имеет нечетное число пересечений с линями границ области. Важнейшим свойством предлагаемого способа является то, что для определения положения частей ломаной линии относительно границ области используются точки на ломаной линии, которые отстоят от границ области на расстояние, не меньшее фиксированного значения Второй технический результат, достигающийся в результате выполнения предлагаемого способа, состоит в расширении возможностей выполнения логических операций над ломаной линией и областью. Известные способы выполнения логических операций над ломаной линией и областью позволяют выполнять операции только для такой области, границы которой не имеют самопересечений и взаимных пересечений. Предлагаемый способ позволяет обрабатывать области, границы которых могут иметь самопересечения и взаимные пересечения. При этом внутренности областей определяются как геометрические места точек, для которых какой-либо луч, выходящий из данной точки, имеет нечетное число пересечений с линями границ области. Это расширение области применения способа имеет важное значение для автоматизации технологических операций обрезки линейных объектов по границам заданной области, используемых в картографическом производстве. При выполнении операции обрезки часто встречается ситуация, когда граница области, по которой производят обрезку, имеет дефекты в виде мелких петель границы, возникающих в результате ошибок оператора или из-за ошибок округления. В этих случаях известные способы вычисления пересечения линейного объекта с областью оказываются неработоспособными, и оператор вынужден затрачивать значительное время на отыскание и устранение мелких петель контуров. Предлагаемый способ выполнения логических операций над ломаной линией и областью лишен этого недостатка. Возможно несколько вариантов задания частей ломаной линии. Например, часть ломаной линии может быть задана указанием начальной точки и длиной этой части. Часть ломаной линии может быть задана указанием координат начальной и конечной точки с указанием того, на каких звеньях ломаной линии эти точки находятся (это необходимо, поскольку ломаная линия в общем случае может иметь петли, т.е. одной и той же точке на плоскости может соответствовать несколько точек ломаной линии). Предпочтительным способом задания частей ломаной линии является способ, состоящий в том, что начальную и конечную точку части ломаной линии задают указанием номера прямолинейного отрезка ломаной линии и доли длины этого отрезка, соответствующей положению начальной или конечной точки части ломаной линии на этом прямолинейном отрезке ломаной линии. Таким образом, часть ломаной линии задают как пары ((m, a), (n, b)), где m и n – номера прямолинейных отрезков, на которых расположены начальная и конечная точки части ломаной линии, а значения 0 Наряду с изложенным способом решения первой задачи, при котором пограничные части ломаной линии не учитываются при формировании результирующего изображения частей ломаной линии, развитие этого способа предполагает учет пограничных частей ломаной линии. Получаемые при этом результаты с точностью Способ получения укрупненных частей ломаной линии, лежащих как внутри, так и вне области, состоит в том, что после получения пограничных, внутренних и (или) внешних частей ломаной линии производят укрупнение частей ломаной линии, лежащих внутри (вне) области. Для этого сначала приписывают им тип t, равный -1, 0 или 1 в зависимости от того, лежит эта часть внутри области, в Такой способ формирования частей ломаной линии, лежащих внутри (вне) области, обеспечивает получение еще одного технического результата, состоящего в устранении дробления ломаной линии на слишком мелкие части в ситуации, когда ломаная линия проходит вблизи границы области, периодически заходя внутрь области и выходя из нее. Это соответствует известному картографическому правилу, состоящему в том, что при нарезке карты на листы в подобной ситуации допускается слегка деформировать линейный объект, чтобы обеспечить достаточно большую протяженность получаемых в результате обрезки объектов (обычно не менее 5-10 мм в масштабе карты). Решение второй задачи достигается за счет формирования изображений границ областей, полученных в результате применения заданной логической операции к двум многоугольным областям, каждая из которых определена на плоскости в виде набора многоугольных контуров, имеющего внешнюю границу и, возможно, границы хотя бы одной дыры, где в результате выполнения указанных операций получаются наборы многоугольных областей, причем для формирования результата операции определяют многоугольники, являющиеся границами указанных многоугольных областей результата, с точностью В отличие от известных способов выполнения логических операций над областями в предлагаемом способе не производят точного вычисления точек пересечения границ исходных ломаных. Такой способ формирования границ результата обеспечивает достижения основного технического результата, состоящего в повышении надежности выполнения операций над многоугольными областями. Под надежностью здесь понимается вероятность правильно полученных результатов выполнения операций среди всех возможных пар исходных областей. Следует заметить, что ввиду конечной разрядности машинного представления координат вершин границ областей число всех возможных вариантов исходных данных конечно, и тем самым определение вероятности корректно (в отличие от известного парадокса Бюффона здесь имеется естественное определение вероятностной меры, связанное с конечно-разрядным представлением исходных данных). Второй технический результат, получающийся в результате выполнения предлагаемого способа, состоит в расширении возможностей выполнения логических операций над многоугольными областями. Известные способы выполнения логических операций над областями позволяют выполнять операции только над такими областями, границы которых не имеют самопересечений и взаимных пересечений. Предлагаемый нами способ позволяет обрабатывать области, границы которых могут иметь самопересечения и взаимные пересечения. При этом внутренности областей определяются как геометрические места точек, для которых какой-либо луч, выходящий из данной точки, имеет нечетное число пересечений с линиями границ области. Это расширение области применения способа имеет важное значение для автоматизации технологических операций обрезки объектов, например, по границе номенклатурного листа, используемых в картографическом производстве. При выполнении операции обрезки часто встречается ситуация, когда обрезаемый объект имеет дефекты в виде мелких петель границы, возникающих в результате ошибок оператора или из-за ошибок округления. В этих случаях известные способы вычисления пересечения объекта с областью листа плана или карты оказываются неработоспособными, и оператор вынужден затрачивать значительное время на отыскание и устранение мелких петель контуров. Предлагаемый способ выполнения логических операций над многоугольными областями лишен этого недостатка. Изобретение поясняется чертежами, где: Фиг.1. Сравнение надежности определения взаимной ориентации контуров. Фиг.2. Положение отрезка относительно Фиг.3. Определение точки входа отрезка в Фиг.4. Точный результат пересечения областей. Фиг.5. Предпочтительный приближенный результат пересечения областей. Фиг.6. Переход границы объединения областей с границы одной области на границу другой области. Фиг.7. Переход границы объединения областей с границы одной области на другую часть границы той же области. Фиг.8. Возникновение дополнительной дырки при объединении областей. Фиг.9. Возникновение дополнительной области из дырок при пересечении областей. Фиг.10. Случай пересечения ломаных линий с одинаковыми направлениями. Фиг.11. Случай пересечения ломаных линий с разными направлениями. Осуществление изобретения 1. Реализуемость способа выполнения операции над ломаной линией и областью 1.1. Описание способа в целом Компьютерный способ формирования изображения частей ломаной линии, лежащих как внутри, так и вне многоугольной области, заданной на плоскости в виде набора многоугольных контуров, имеющего внешнюю границу и, возможно, границы хотя бы одной дыры, с заданной точностью Определение пограничных частей ломаной линии, лежащих в После того, как будут вычислены пограничные части ломаной линии, оставшиеся части вычисляют как дополнение объединения всех пограничных частей до всей ломаной линии. По существу, здесь уже не требуется никаких вычислений, а производят только перегруппировку полученных данных. Способ получения оставшихся частей ломаной линии по набору пограничных частей излагается ниже в п.1.4. Возможно несколько вариантов задания частей ломаной линии. Например, часть ломаной линии может быть задана указанием начальной точки данной части и длины этой части. Часть ломаной линии может быть задана указанием координат начальной и конечной точки с указанием того, на каких звеньях ломаной линии эти точки находятся (это необходимо, поскольку ломаная линия в общем случае может иметь петли, т.е. одной и той же точке на плоскости может соответствовать несколько точек ломаной линии). Предпочтительным способом задания частей ломаной линии является способ, изложенный в п.1.3. Он состоит в том, что начальную и конечную точку части ломаной линии задают указанием номера отрезка ломаной линии и доли длины этого отрезка, соответствующей положению начальной или конечной точки части ломаной линии на этом отрезке ломаной линии. После того, как определены части ломаной линии, лежащие вне Способ определения частей ломаной линии, лежащих внутри (вне) области и не пересекающихся с Выбор точек в каждой из частей ломаной линии, не пересекающихся с Координаты (х, у) произвольной точки на ломаной линии (m, а) определяют следующим образом. Если а=0, то (х, у) полагают равными координатам (хm, уm) точки Аm. В противном случае определяют номер m1=m+1 следующей точки (если m1=n, то полагают m1=0) и вычисляют координаты (х, у) по формулам x=xm+(xm1-xm)*а, у=уm+(уm1-уm)*а. Из полученных для всех М частей границ {(mk, аk), (nk, bk)} точек с координатами (xk, уk) отбирают те точки, которые лежат внутри (вне) области. Для этого проводят горизонтальный луч из точки (xk, уk) в направлении возрастания координаты х и подсчитывают число пересечений этого луча с отрезками, образующими границы области. Если число пересечений нечетно, то точка (xk, уk) лежит внутри области; если число пересечений четно, то точка (xk, уk) лежит вне области. Случай близости точки (xk, уk) к границе области исключается, поскольку точка (xk, уk) выбрана из частей ломаной линии, не пересекающихся с Отобрав таким образом из общего списка точек (хk, уk), 0 Возможно несколько вариантов учета пограничных частей ломаной линии, каждый из которых имеет преимущество в той или иной ситуации. Например, можно не включать такие части ломаной линии в результат операции. В случае пересечения ломаной линии с областью это соответствует пересечению ломаной линии с открытой областью, т.е. с областью без границы, а в случае вычитания области из ломаной линии – вычитанию замкнутой области, т.е. областью с границей. Напротив, можно включать такие части ломаной линии в результат операции. В случае пересечения ломаной линии с областью это соответствует пересечению ломаной линии с замкнутой областью, а в случае вычитания области из ломаной линии – вычитанию открытой области. Если пограничные части ломаной линии не включаются в результат операции, то никаких дополнительных действий не требуется. В противном случае может оказаться, что пограничная часть ломаной линии расположена между двумя частями ломаной линии, которые включены в результат. В этом случае производят объединение этих трех частей ломаной линии в одну часть, которая с точностью Изложенный способ определения частей ломаной линии, лежащих внутри и (или) лежащих вне многоугольной области, обеспечивает достижение основного технического результата, состоящего в повышении надежности результата выполнения операции. Природа повышения надежности связана со следующим обстоятельством. В известном способе выполнения геометрических операций над ломаной линией и областью одним из важнейших моментов является определение взаимного расположения двух контуров в окрестности точки их пересечения. В случае большой погрешности определения точки пересечения получаемый результат будет сильно отличаться от правильного. Но даже при точно вычисленной точке пересечения возникает проблема в определении того, входит ломаная линия внутрь области или выходит из нее. Характерный пример приведен на фиг.1. Возможен случай, когда отрезок АВ ломаной линии расположен очень близко к отрезку CD границы области. Эта ситуация очень часто встречается в реальной практике, когда, например, контур Следует заметить, что указанный в предыдущем абзаце случай является очень часто встречающимся в реальном производстве картографической продукции. Типичной ситуацией является то, что контур Заметим, что в реально встречающихся на практике задачах разумная величина Второй технический результат, получающийся в результате выполнения предлагаемого способа, состоит в расширении возможностей выполнения логических операций над ломаной линией и областью, что связано с возможностью выполнения операции над ломаной линией и областью в случае, когда границы области могут иметь самопересечения и взаимные пересечения. Вышеизложенный способ определения того, лежит рассматриваемая часть ломаной линии внутри или вне области с границей без самопересечений, путем определения четности числа пересечений луча, выходящего из какой-либо точки рассматриваемой части, с границами области, является известным способом и описан, например, в [Препарата Ф, Шеймос М. Вычислительная геометрия: Введение. М, «Мир», 1989, с.59]. Мы используем обобщение этого способа на области, границы которых могут иметь самопересечения и взаимные пересечения. В этом случае под внутренностью области понимается совокупность точек плоскости, для которых любой луч, выходящий из данной точки, имеет нечетное число пересечений с границами области. 1.2. Предпочтительный способ определения пограничных частей ломаной линии 1.2.1. Общее описание Предпочтительный способ определения пограничных частей ломаной линии состоит в выполнении трех этапов: сначала определяют список всех пар (I, II), где I – прямолинейный отрезок ломаной линии, II – прямолинейный отрезок ломаной границы области, причем I пересекает Возможность реализации всех указанных этапов обосновывается ниже в п.п.1.2.2-1.2.4 соответственно. 1.2.2. Определение всех пар из прямолинейного отрезка ломаной линии и прямолинейного отрезка контура границы области, где первый отрезок пересекает Способ определения всех пар (I, II), где I – прямолинейный отрезок ломаной линии, II – прямолинейный отрезок контура границы области, причем отрезок I пересекает Правильность этого способа обосновывается с помощью следующих рассмотрений. Определение факта пересечения одного отрезка I с 1 – отрезки I и II пересекаются; 2 – расстояние от начала отрезка II до отрезка I меньше 3 – отрезок I не пересекает В самом деле, пусть отрезки I и II не пересекаются, но отрезок I пересекает Таким образом, все случаи, когда отрезок I пересекает 1.2.3. Определение пересечения отрезка I с Пересечение отрезка I с Способы определения значений а и b аналогичны, поэтому ограничимся описанием способа определения значения а (см. фиг.3). Способ определения доли начала отрезка I, которая не входит в 1.2.4. Формирование частей ломаной линии, лежащих в Способ формирования частей ломаной линии, лежащих в Пусть A0A1 (m0, с0)<(m1, c1)< формируют последовательность связных частей замкнутой ломаной линии {(m0, с0), (m1, c1)}, из которой отбирают только те связные части, которые входят в какую-либо из исходных частей ломаной линии {(ik, ak), (ik, bk)}, 0 Пусть теперь A0A1 (m0, с0)<(m1, c1)< формируют последовательность связных частей замкнутой ломаной линии {(m0, c0), (m1, c1)}, Из этой последовательности отбирают только те связные части, которые входят в какую-либо из исходных частей ломаной линии {(ik, ak), (ik, bk)}, 0 1.3. Задание частей ломаной линии Введем понятие точки на ломаной линии и понятие сегмента ломаной линии. Пусть A0A1 Произвольная связная часть ломаной линии задается парой {(i, a), (j, b)} точек на ломаной линии, где (i, а) – начальная точка, (j, b) – конечная точка связной части ломаной линии. При этом считается, что i+а>j+b допустимо только в случае замкнутой ломаной линии, и в этом случае указанная часть ломаной линии содержит начальную точку А0. В частности, полученным в п.1.2.3 пересечениям отрезков AiAi+1 с 1.4. Получение оставшихся частей ломаной линии по набору пограничных частей Способ получения оставшихся частей ломаной линии по набору пограничных частей {(m0, с0), (m1, c1)}, Если ломаная линия является замкнутой, то в качестве оставшихся частей ломаной линии берут последовательность частей {(m1, c1), (m2, c2)}, Если ломаная линия является незамкнутой, то в качестве оставшихся частей ломаной линии берут последовательность частей {(0, 0), (m0, с0)}, {(m1, c1), (m2, c2)}, 1.5. Укрупнение частей ломаной линии Способ укрупнения частей ломаной линии (см. п.1.1) состоит в следующем. Пусть {((mj, aj), (nj, bj))}, 0 Сначала упорядочивают эти части в соответствии с порядком на множестве точек на ломаной линии, введенном в п.1.3. Для упрощения обозначений будем считать, что исходная последовательность {((mj, aj), (nj, bj), tj)}, 0 Последовательно просматривают все части ломаной линии, и для каждой части ломаной линии ((mj, aj), (nj, bj), tj), для которой tj=0, рассматривают предыдущую (j-1)-ю и следующую (j+1)-ю части ломаной линии. При этом для замкнутой ломаной линии вычитание и прибавление 1 производят по модулю общего числа s частей ломаной линии, а для незамкнутой ломаной линии просматривают все части ломаной линии, кроме первой и последней. Если конец предыдущей части не совпадает с началом рассматриваемой части ломаной линии и начало следующей части не совпадает с концом рассматриваемой части, то рассматриваемую часть ломаной линии удаляют из последовательности {((mj, aj), (nj, bj))}, уменьшая номера всех последующих частей на 1 и уменьшая общее число частей на 1. Если конец предыдущей части совпадает с началом рассматриваемой части ломаной линии и начало следующей части совпадает с концом рассматриваемой части, то тройку ((mj-1, aj-1), (nj-1, bj-1), tj-1), ((mj, aj), (nj, bj), tj), ((mj+1, aj+1), (nj+1, bj+1), tj+1) заменяют одной частью ломаной линии ((mj-1, аj-1), (nj+1, bj+1), tj-1), уменьшая номера всех последующих частей на 2 и уменьшая общее число частей на 2. Смысл такого преобразования последовательности частей ломаной линии состоит в следующем. Если для рассматриваемой части ломаной линии ((mj, аj), (nj, bj), tj), для которой tj=0, конец предыдущей части не совпадает с началом рассматриваемой части ломаной и начало следующей части не совпадает с концом рассматриваемой части, то это означает, что при движении вдоль ломаной линии ее часть, непосредственно предшествующая рассматриваемой части, лежит вне Если для рассматриваемой части ломаной линии ((mj, аj), (nj, bj), tj), для которой tj=0, конец предыдущей части совпадает с началом рассматриваемой части ломаной линии и начало следующей части совпадает с концом рассматриваемой части, то это означает, что при движении вдоль данной ломаной линии ее часть, непосредственно предшествующая рассматриваемой части, лежит вне 2. Реализуемость способа выполнения операции над двумя областями 2.1. Описание способа в целом Компьютерный способ формирования изображения границ одной или нескольких областей, полученных в результате применения заданной логической операции к двум многоугольным областям, определенным каждая на плоскости в виде набора многоугольных контуров, имеющего внешнюю границу и, возможно, границы хотя бы одной дыры, и для каждой из упомянутых многоугольных областей эти границы могут иметь самопересечения и (или) взаимные пересечения, с заданной точностью Далее из всех найденных пограничных частей отбирают те, которые имеют скорректированное направление обхода, совпадающее со скорректированным направлением обхода другого многоугольного контура, или скорректированное направление обхода, противоположное скорректированному направлению обхода другого многоугольного контура, в соответствии с упомянутой заданной логической операцией. Направление обхода контура задается последовательностью координат вершин многоугольного контура, введенной в память компьютера. В то же время для определения того, какие пограничные части контуров границ войдут в качестве частей границ областей, составляющих результат выполнения логической операции над двумя областями, важны не направления контуров границ, а скорректированные направления, определяемые ниже. Если бы контуры границ не имели самопересечений и взаимных пересечений, то всегда можно было бы изменить порядок обхода контура так, чтобы при обходе контура ограничиваемая им область была расположена слева от контура (обход внешней границы области против часовой стрелки и обход границ дыр по часовой стрелке). При наличии у контура самопересечений или при наличии взаимных пересечений контуров так сделать нельзя, и вместо обеспечения единого направления обхода контура, при котором ограничиваемая им область всегда остается по одну сторону от этого контура, приходится вводить локальное понятие скорректированного направления обхода. Точки самопересечения замкнутого контура границы области и точки пересечения этого контура с другими контурами границы области разбивают данный контур на части, для каждой из которых определяют скорректированное направление обхода следующим образом. Если при обходе данной части ломаной линии, являющейся контуром границы области, в соответствии с порядком вершин ломаной линии, ограничиваемая этим контуром область лежит слева от этой ломаной линии, то под скорректированным направлением понимают упомянутое направление обхода ломаной линии. В противном случае под скорректированным направлением понимают противоположное направление. Описание того, какие направления надо использовать (совпадающие или противоположные) в зависимости от логической операции, также приводится ниже в пп.2.2-2.4. Сам способ отбора пограничных частей с учетом направления обхода излагается ниже в п.2.5. После того как будут определены части границ исходных областей, входящие в границы областей, являющихся результатом выполнения операции, производят формирования границ результата логической операции над областями из частей границ исходных областей и дополнительных коротких отрезков длины Наконец, формируют на устройстве вывода компьютера изображения упомянутых границ областей из найденных на предыдущем шаге частей. В качестве устройства вывода может использоваться дисплей компьютера. Другим вариантом может быть запись координат полученных границ областей в базу данных с тем, чтобы в последствии выдавать данные на дисплей без повторения уже проведенных вычислений. 2.2. Пересечение областей На фиг.4 изображены две области I и II, первая из которых является шестиугольником неправильной формы, а вторая – треугольником. Область ABCDEF, являющаяся точным их пересечением, заштрихована. Заданная требуемая точность вычислений Из сравнения фиг.4 и фиг.5 видно, что как точное пересечение областей, так и приближенное, имеют границы, содержащие часть LDK границы области I, лежащую вне – части границы области I, лежащей вне – части границы области II, лежащей вне – тех частей границ области I, которые лежат в – тех частей границ области II, которые лежат в – дополнительных коротких сторон, каждая из которых имеет длину 2.3. Объединение областей Рассмотрения, аналогичные приведенным в п.2.2, показывают, что граница приближенного объединения областей может быть составлена из: – части границы области I, лежащей вне – части границы области II, лежащей вне – тех частей границ области I, которые лежат в – тех частей границ области II, которые лежат в – дополнительных коротких сторон, каждая из которых имеет длину 2.4. Вычитание областей Рассмотрения, аналогичные приведенным в п.2.2, показывают, что граница приближенного результата вычитания области II из области I может быть составлена из: – части границы области I, лежащей вне – части границы области II, лежащей вне – тех частей границ области I, которые лежат в – тех частей границ области II, которые лежат в – дополнительных коротких сторон, каждая из которых имеет длину 2.5 Способ отбора пограничных частей с учетом скорректированных направлений Способ формирования пограничных частей границ одной области, имеющих надлежащее скорректированное направление относительно границ другой области, состоит в следующем. Пусть A0A1 Сначала производят отбор тех частей ломаной линии {(ik, ak), (ik, bk)}, для которых прямолинейные отрезки AkAk+1 и CkDk контуров границ первой и второй области соответственно имеют надлежащие скорректированные направления (одинаковые или противоположные). При этом возможна такая ситуация, когда, например, отрезок CkDk контура границы второй области пересекается с некоторым отрезком той же границы второй области, так что образуется петля, или пересекается с другим контуром границы второй области, причем точка пересечения Е лежит в Чтобы не менять обозначений, мы обозначим число уже отобранных частей снова через N. После этого упорядочивают все 2N точек на ломаной линии, соответствующие началам и концам указанных частей в соответствии с отношением порядка, введенным в п.1.3. По полученной последовательности (m0, с0)<(m1, c1)< формируют последовательность связных частей замкнутой ломаной {(m0, с0), (m1, c1)}, из которой оставляют только те связные части, которые входят в какую-либо из отобранных частей ломаной линии {(ik, ak), (ik, bk)}, 0 2.6. Способ формирования границ результата логической операции над областями из частей границ исходных областей и дополнительных коротких отрезков 2.6.1. Общие положения Исходные данные для формирования границ результата логической операции над двумя областями из частей границ исходных областей и дополнительных коротких отрезков представляет собой совокупность пограничных частей границ каждой из исходных областей, имеющих надлежащее направление относительно границ другой области, а также совокупность укрупненных частей границ каждой из исходных областей, лежащих внутри или вне другой области (в соответствии с типом операции, см. пп.2.2-2.4). Способ формирования границ областей, в совокупности составляющих результат логической операции, из границ двух областей состоит в последовательном формировании границ результата путем прохождения по всем указанным в предыдущем абзаце укрупненным частям границ первой и второй области. Если таких частей нет, то это означает, что все отрезки границы первой области лежат в Если существуют укрупненные части границ первой и второй области, то собирают границы областей результата путем обхода укрупненных частей границ исходных областей (пп.2.6.2-2.6.4), получая последовательности частей границ двух исходных областей I и II, из которых состоят границы областей результата операции. В отличие от частей границ исходных областей, задаваемых тройками ((m, a), (n, b), t) (см. п.1.5), эти части границ задают четверками ((m, а), (n, b), t, с). Дополнительная компонента с принимает значения 1 или -1 в зависимости от того, проходится часть границы ((m, а), (n, b), t) исходной области в том же направлении, что и исходное направление обхода границы исходной области, или в противоположном направлении. 2.6.2. Объединение областей В соответствии с терминологией п.1.5, все части границ исходных областей, из которых должны формироваться границы объединения областей, имеют тип 0 или 1, поскольку части границ одной области, лежащие внутри другой области, не входят в число границ, из которых формируются границы результата объединения областей. Прежде всего формируют внешний контур результата. Легко видеть, что внешний контур объединения областей является подмножеством объединения внешних контуров исходных областей. Для формирования этого внешнего контура из всех укрупненных частей внешних границ исходных областей выбирают ту часть границы, для которой какая-либо ее вершина, начало или конец имеют минимальное значение координаты х. Это гарантирует то, что эта часть границы будет частью именно внешнего контура результата, а не частью контура какой-либо из его дырок. Если эта часть границы совпадает со всем контуром, то этот контур и будет искомым внешним контуром объединения областей. Пусть рассматриваемая часть границы не совпадает ни с каким контуром границ исходных областей. Если она имеет тип 0, то согласно рассмотрениям п.1.5 она следует за частью границы, имеющей тип 1, или непосредственно за ней следует часть границы, имеющая тип 1, и ясно, что эта соседняя часть границы типа 1 войдет во внешний контур объединения областей. В этом случае переходят от рассмотрения данной части границы, имеющей тип 0, к рассмотрению соседней с ней части границы, имеющей тип 1. Итак, начиная формирование внешнего контура объединения областей, можно начать с некоторой части границы внешнего контура какой-либо из исходных областей, без ограничения общности считая, что рассматриваемая часть А имеет тип 1. Для определенности пусть эта часть принадлежит внешней границе области I. Части А приписывают направление обхода с=1. Непосредственно за ней идет часть контура I, лежащая в В первом случае (фиг.6) из нескольких таких точек выбирают первую по направлению движения, имеющую координаты (х, у). Поскольку точка (х, у) является началом или концом части типа 1 внешнего контура области II, то от нее начинается или в ней заканчивается некоторая часть В границы области II типа 1. Тогда принимают решение о том, что граница объединения областей делает переход с части А границы области I на часть В границы области II. Если точка (х, у) является началом части В границы области II, то части В приписывают направление обхода с=1. Если точка (х, у) является концом части В границы области II, то части В приписывают направление обхода с=-1. Если точка (х, у) является и началом, и концом части В границы области II, т.е. граница области II имеет петлю, то направление обхода выбирают так, чтобы эта охватываемая этой петлей область находилась с той же стороны от петли, что и формируемая область относительно части границы А. Во втором случае (фиг.7) часть В границы области II лежит целиком внутри Действуя таким образом, составляют последовательность частей внешних контуров областей I и II, последовательное прохождение которых дает внешнюю границу объединения областей. Этот процесс завершают, когда приходят в ту часть А, с которой и начали этот процесс. Затем формируют контуры дырок области, являющейся объединением исходных областей I и II. Для этого определяют те части типа 1 внешних контуров областей I и II, которые остались не использованными при формировании внешнего контура объединения областей (см. фиг.8), и при их наличии из них и из частей типа 1 дырок исходных областей формируют одну или несколько дырок объединения областей. Это производят путем процесса, аналогичного описанному процессу определения внешнего контура объединения. 2.6.3. Пересечение областей В соответствии с терминологией п.1.5, все части границ исходных областей, из которых должны формироваться границы объединения областей, имеют тип 0 или -1, поскольку части границ одной области, лежащие вне другой области, не входят в число границ, из которых формируются границы результата объединения областей. Пересечения двух областей в общем случае может состоять из нескольких областей, и их формирование производят последовательно. Для каждой очередной области, входящей в состав пересечения, прежде всего формируют внешний контур результата. Для формирования очередного внешнего контура из всех еще не использованных укрупненных частей границ исходных областей выбирают ту еще не использованную часть границы, для которой какая-либо ее вершина, начало или конец имеют минимальное значение координаты х. Это гарантирует то, что эта часть границы будет частью именно внешнего контура результата, а не частью контура какой-либо из его дырок. Если эта часть границы совпадает со всем контуром, то этот контур и будет искомым очередным внешним контуром пересечения областей. Пусть рассматриваемая часть границы не совпадает ни с каким контуром границ исходных областей. Если она имеет тип 0, то согласно рассмотрениям п.1.5 она следует за частью границы, имеющей тип -1, или непосредственно за ней следует часть границы, имеющая тип -1, и ясно, что эта соседняя часть границы типа -1 войдет во внешний контур пересечения областей. В этом случае переходят от рассмотрения данной части границы, имеющей тип 0, к рассмотрению соседней с ней части границы, имеющей тип -1. Процесс формирования очередного внешнего контура пересечения аналогичен процессу формирования внешнего контура объединения. Затем формируют контуры дырок очередной области, являющейся частью пересечения исходных областей I и II. Для этого определяют дырки областей I и II, которые остались еще не использованными при формировании пересечения и которые лежат внутри сформированного очередного внешнего контура пересечения, и при их наличии из их частей типа -1 формируют одну или несколько дырок пересечения областей. Это производят путем процесса, аналогичного описанному процессу определения внешнего контура объединения. Из оставшихся неиспользованными частей границ дырок типа -1 формируют границы областей, также входящих в состав пересечения областей и лежащих внутри дырок (см. фиг.9). На этой фигуре исходные области показаны заштрихованными под углом 45 и 135 градусов, а такая дополнительная область показана более мелкой штриховкой. 2.6.4. Вычитание областей В соответствии с терминологией п.1.4, при вычитании области II из области I все части границ исходной области I, из которых должны формироваться границы объединения областей, имеют тип 0 или -1, поскольку части границ вычитаемой области, лежащие вне другой области, не входят в число границ, из которых формируются границы результата объединения областей. Аналогично, все части границ исходной области II, из которых должны формироваться границы объединения областей, имеют тип 0 или 1. Результат вычитания области II из области I в общем случае может состоять из нескольких областей, и их формирование производят последовательно. Для каждой очередной области, входящей в состав результата вычитания, прежде всего формируют внешний контур результата. Для формирования очередного внешнего контура из всех еще не использованных укрупненных частей границ исходных областей выбирают ту еще не использованную часть границы, для которой какая-либо ее вершина, начало или конец имеют минимальное значение координаты х. Это гарантирует то, что эта часть границы будет частью именно внешнего контура результата, а не частью контура какой-либо из его дырок. Если эта часть границы совпадает со всем контуром, то этот контур и будет искомым очередным внешним контуром результата вычитания областей. Пусть рассматриваемая часть границы не совпадает ни с каким контуром границ исходных областей. Если она имеет тип 0, то согласно рассмотрениям п.1.5 она следует за частью границы, имеющей тип -1 или тип 1 (в зависимости от того, является она частью границы области I или области II), или непосредственно за ней следует часть границы, имеющая тип -1 (или 1), и ясно, что эта соседняя часть границы типа -1 (или 1) войдет во внешний контур пересечения областей. В этом случае переходят от рассмотрения данной части границы, имеющей тип 0, к рассмотрению соседней с ней части границы, имеющей тип -1 (или 1). Процесс формирования очередного внешнего контура результата вычитания аналогичен процессу формирования внешнего контура объединения. Затем формируют контуры дырок очередной области, являющейся частью результата вычитания области II из области I. Для этого определяют дырки областей I и все контура границы области II, которые остались еще не использованными при формировании пересечения и которые лежат внутри сформированного очередного внешнего контура пересечения, и при их наличии из их частей типа -1 (соответственно 1) формируют одну или несколько дырок результата вычитания областей. Это производят путем процесса, аналогичного описанному процессу определения внешнего контура объединения. 2.7. Определение координат вершин ломаных, составляющих границы результата Исходными данными для получения координат вершин ломаных, составляющих границы результата выполнения логических операций над областями, является совокупность последовательностей {((mj, aj), (nj, bj), tj, cj)}, 0 Последовательность координат вершин ломаной линии, являющейся очередной границей области, входящей в результат выполнения геометрической операции, формируют путем последовательного прохождения по всем отрезкам последовательности {((mj, aj), (nj, bj), tj, сj)}, 0 Для каждой части ((mj, aj), (nj, bj), tj, сj) границы одной из исходных областей формируют последовательность ее внутренних вершин следующим образом. Пусть эта часть границы является частью исходной замкнутой ломаной линии, имеющей Nj вершин. Если mj+aj Формирование координат вершин ломаной линии, составляющей очередную границу результата, завершают добавлением дополнительных вершин между соседними последовательностями вершин, соответствующими соседним элементам последовательности {((mj, aj), (nj, bj), tj, сj)}, 0 Пусть ((mj, aj), (nj, bj), tj, cj) и ((mj+1, aj+1), (nj+1, bj+1), tj+1, cj+1) – две последовательные части исходных ломаных линий, входящих в границу результата выполнения логической операции. Если cj=1 и cj+1=1, то необходимо состыковать конец первой части с началом второй. Если cj=1 и cj+1=-1, то необходимо состыковать конец первой части с концом второй. Если сj=-1 и сj+1=1, то необходимо состыковать начало первой части с началом второй. Если сj=-1 и cj+1=-1, то необходимо состыковать начало первой части с концом второй. Во всех четырех случаях действуют аналогичным образом, и для определенности рассмотрим только первый случай. Итак, пусть ((mj, аj), (nj, bj), tj, cj) и ((mj+1, aj+1), (nj+1, bj+1), tj+1, cj+1) – две последовательные части исходных ломаных линий, входящих в границу результата выполнения логической операции, причем сj=cj+1=1. Способ стыковки двух частей границы несколько отличается в зависимости от того, является текущая граница внешней границей области или границей дырки. Рассмотрим сначала случай внешней границы, причем указанные две части ломаных линий принадлежат разным областям. Здесь возможны два принципиально разных случая, представленные соответственно на фиг.10-11. Используются следующие обозначения: А – точка входа первой части ломаной линии в В случае фиг.10 проектируют точку А на ломаную линию CD, что дает точку А’, и проектируют точку D на ломаную линию АВ, что дает точку D’. Это дает два возможных пути из точки А в точку D: AA’D и AD’D. Из этих двух путей выбирают наилучший по некоторому критерию, выбор которого может зависеть от конкретной задачи. Полученные в результате три точки вставляют в формируемую последовательность точек вершин ломаной линии результата. В случае фиг.11 проектируют точку А на ломаную линию CD, что дает точку А’, и проектируют точку D на ломаную линию АВ, что дает точку D’, и в исходной последовательности вершин ломаной линии результата заменяют точку А на точку D’ или заменяют точку В на точку А’. Из этих двух путей выбирают наилучший по некоторому критерию, выбор которого может зависеть от конкретной задачи. В случае формирования границы дырки действуют так же, как и при формировании внешнего контура, но при формировании переходом с одной части границы на другую дополнительно следят за тем, чтобы граница формируемой дырки не выходила за пределы внешнего контура. В том случае, если такой случай возникает, все вершины границы дырки, оказавшиеся вне внешнего контура, заменяют проекциями этих точек на внешний контур, что обеспечивает невыход границы дырки за пределы внешнего контура.
Формула изобретения
1. Компьютерный способ формирования изображения частей ломаной линии, лежащих как внутри, так и вне многоугольной области, заданной на плоскости в виде набора многоугольных контуров, имеющего внешнюю границу и, возможно, границы хотя бы одной дыры, и все эти границы могут иметь самопересечения и (или) взаимные пересечения, причем изображения частей упомянутой ломаной линии формируют с заданной точностью 2. Способ по п.1, отличающийся тем, что устройство вывода данных упомянутого компьютера является дисплеем. 3. Способ по п.1, отличающийся тем, что устройство вывода данных упомянутого компьютера является базой данных. 4. Способ по п.1, отличающийся тем, что для определения частей ломаной линии, лежащих в 5. Способ по п.1, отличающийся тем, что каждая часть ломаной линии задается парой ((mj, aj), (nj, bj)) разных точек на ломаной линии, соответствующих началу и концу части ломаной линии, а каждая точка на ломаной линии является парой, первая компонента которой является номером звена ломаной линии, содержащего данную точку, а вторая компонента – долей расстояния от начала прямолинейного отрезка ломаной линии до данной точки в общей длине прямолинейного отрезка ломаной линии, причем для незамкнутой ломаной линии всегда выполняется условие mj+aj 6. Способ по п.5, отличающийся тем, что после определения частей ломаной линии, лежащих в 7. Способ по п.5, отличающийся тем, что для определения пограничных частей ломаной линии упорядочивают все точки на ломаной линии, соответствующие началам и концам пересечений прямоугольных отрезков ломаной линии с 8. Компьютерный способ формирования изображения границ одной или нескольких областей, полученных в результате применения заданной логической операции к двум многоугольным областям, определенным каждая на плоскости в виде набора многоугольных контуров, имеющего внешнюю границу и, возможно, границы хотя бы одной дыры, и для каждой из упомянутых многоугольных областей эти границы могут иметь самопересечения и (или) взаимные пересечения, причем изображение результата выполнения упомянутой логической операции формируют с заданной точностью 9. Способ по п.8, в котором выбирают заданную логическую операцию из группы, состоящей из пересечения, объединения и вычитания. 10. Способ по п.8, отличающийся тем, что устройство вывода данных упомянутого компьютера является дисплеем. 11. Способ по п.8, отличающийся тем, что устройство вывода данных упомянутого компьютера является базой данных. 12. Способ по п.8, отличающийся тем, что сначала определяют части границ одной области, лежащие в 13. Способ по п.8, отличающийся тем, что для определения частей границ одной области, лежащих в 14. Способ по п.8, отличающийся тем, что области, входящие в результат выполнения операции, формируют последовательно путем обхода частей границ исходных областей, причем при формировании каждой очередной области результата сначала формируют ее внешний контур, а затем контуры ее дыр и, возможно, дополнительных областей результата, лежащих внутри дыр.
РИСУНКИ
TH4A – Переиздание описания изобретения к патенту Российской Федерации
Причина переиздания: Коррекция в текстах формулы и описания изобретения
Извещение опубликовано: 20.04.2009 БИ: 11/2009
,> ,> |
||||||||||||||||||||||||||

 -окрестности границы области, определения оставшихся частей ломаной линии и выбора из них тех частей, которые лежат внутри или вне области. Этот способ формирования изображения частей ломаной линии, лежащих как внутри, так и вне многоугольной области, используется в способе формирования изображения границ одной или нескольких областей, полученных в результате применения заданной логической операции к двум многоугольным областям. 2 н. и 12 з.п. ф-лы, 11 ил.
-окрестности границы области, определения оставшихся частей ломаной линии и выбора из них тех частей, которые лежат внутри или вне области. Этот способ формирования изображения частей ломаной линии, лежащих как внутри, так и вне многоугольной области, используется в способе формирования изображения границ одной или нескольких областей, полученных в результате применения заданной логической операции к двум многоугольным областям. 2 н. и 12 з.п. ф-лы, 11 ил. а, b<1 определяют положение начала и конца части ломаной линии на соответствующем прямолинейном отрезке.
а, b<1 определяют положение начала и конца части ломаной линии на соответствующем прямолинейном отрезке. An-1 – замкнутая или незамкнутая ломаная линия, содержащая n вершин, и {(m0, c0), (m1, c1)} – часть этой ломаной линии, не пересекающаяся с
An-1 – замкнутая или незамкнутая ломаная линия, содержащая n вершин, и {(m0, c0), (m1, c1)} – часть этой ломаной линии, не пересекающаяся с 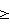 0, а+b<1, где а – доля отрезка I, начиная с его начала, которая не входит в
0, а+b<1, где а – доля отрезка I, начиная с его начала, которая не входит в  0).
0). находят пограничные части упомянутой ломаной линии, лежащие в
находят пограничные части упомянутой ломаной линии, лежащие в