Патент на изобретение №2335756

(54) ВОЛНОВОЙ СПОСОБ КОНТРОЛЯ СВОЙСТВ МАТЕРИАЛОВ

(57) Реферат:

Изобретение относится к методу контроля материалов. Сущность: изделие взвешивают, определяют его массу, измеряют длину и диаметр. Наносят ударным механизмом удар по образцу, закрепленному в держателе только с одной стороны, в двух направлениях – по вертикальной оси сверху (сжимающий удар) и по касательной у нижнего свободного края образца (касательный удар), записывают на ЭВМ через микрофон, находящийся в 20 см от образца, собственные волны образца материала от двух ударов (две записи), полученные записи подвергают спектральному анализу. Выявляют из первой записи резонансную частоту от сжимающего удара, выявляют из второй записи касательную резонансную частоту, вводят полученные результаты в ЭВМ. Проводят расчет на ЭВМ. Распечатывают результат контроля, характеризующийся резонансными частотами, связанными с модулем нормальной упругости, модулем сдвига, коэффициентом Пуассона, твердостью по Бринеллю, временным сопротивлением, относительным сужением, относительным удлинением, истинным напряжением при разрыве, пределом текучести, ударной вязкостью, пределом выносливости, сопротивлением усталости. Технический результат: разработка нового вида контроля свойств материалов.

Уровень техники

Волновой способ контроля свойств материалов является новым видом контроля, основанного на акустических эффектах.

Акустические эффекты используются в методах ультразвуковой дефектоскопии и акустической эмиссии.

Так, например, при растяжении образца на разрыв в нем возникают акустические сигналы, фиксируя которые, можно вести наблюдения за изменениями этих сигналов и изменениями прочностных свойств материала, но этот метод требует разрыва образца в отличии от волнового способа, в котором образец остается цел.

Динамический акустический метод позволяет определять модуль нормальной упругости на специальных устройствах, позволяющих вызвать колебания образца, то есть собственную частоту колебаний /1:9/.

Однако для этого надо нагревать образец, что не требуется при волновом способе контроля.

Определяют механические параметры по скорости ультразвука в материале. Так как скорость звука в материале зависит от его модуля упругости и удельной массы, то, зная скорость ультразвука, выводят его корреляционные зависимости от некоторых механических параметров материалов /2:10/.

Наличие корреляционных взаимозависимостей в этом методе контроля требует относительно продолжительной его производственной адаптации, что не требуется при волновом способе контроля.

Ультразвуковой метод контроля в отличие от волнового способа нацелен на выявление трещинообразования, раковин, но не выявляет изменения основных свойств материалов, таких, например, как временное сопротивление, предел текучести, истинное напряжение при разрыве, ударную вязкость.

Для контроля материалов сосудов давления, технологического оборудования компрессорных и газораспределительных станций, трубопроводов газоснабжения, промысловых и напорных трубопроводов, магистральных трубопроводов, технологических трубопроводов, резервуаров для хранения нефтепродуктов, грузоподъемных механизмов, трубопроводов теплосетей, мостовых конструкций, железнодорожных цистерн и деталей вагонов на отсутствие течи применяется акустико-эмиссионный метод. Акустико-эмиссионные испытания проводятся при достаточно большой растущей нагрузке /2:14-15/.

Этот метод ограничивается поиском течи в изделии, в отличие от волнового способа не определяет основные свойства материала.

Виброакустический метод контроля раковин, трещин работающих подшипников позволяет вести контроль этих дефектов, но в отличие от волнового способа не позволяет определять основные свойства материалов /3/.

Контроль твердости по собственным колебаниям для абразивных изделий осуществляется согласно ГОСТ 25961-83 «Инструмент абразивный. Акустический метод контроля физико-механических свойств», стандарту TGL 55047 «Шлифовальные круги. Определение твердости. Акустический метод» (Германия), по ГОСТ 2424-83 «Круги шлифовальные. Технические условия».

Вместо буквенного обозначения степени твердости на кругах маркируется звуковой индекс. Этот метод введен по ГОСТ 2464-82 «Сегменты шлифовальные. Технические условия» и ГОСТ 2456-82 «Бруски шлифовальные. Технические условия» и в качестве основного метода по ГОСТ 21963-82 «Круги отрезные. Технические условия». В соответствии с этим стандартом с 01.01.1986 года на отрезных кругах диаметром менее 600 мм твердость маркируется значением звукового индекса (ЗИ). Аналогичные стандарты были разработаны в Венгрии и Чехословакии. Эти стандарты реализуют возможность контроля твердости абразивных изделий размерами от 3 до 1200 мм. Применение акустического метода для контроля абразивного инструмента регламентировано государственным стандартом ГОСТ 25961-83. По этим ГОСТ параметрами являются скорость звука и звуковой индекс (ЗИ), по которым определяют твердость. Для абразивных инструментов диапазон значений скорости звука разбит на интервалы с шагом 200 м/с, которые образуют звуковой индекс /2:11/.

В этом методе просматривается ограниченность по виду изделия – круги абразивные, и по свойствам: контролируется твердость, в отличии от волнового способа, позволяющего контролировать большее их число.

Раскрытие изобретения.

При возникновении собственных вибраций образца от ударного импульса небольшой силы (1-3 Н) образец становится источником волн, распространяющихся в воздухе, в диапазоне до 20 кГц.

Так как жесткость:

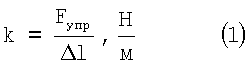
где F_упр – сила упругости, действующая на образец, Н;

l – изменение длины образца, м.

Собственная частота волн, возникших в воздухе от вибраций материала изделия, образовавшихся вследствие сжимающего ударного импульса, f₀ зависит от жесткости как:

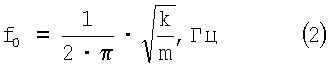
где m – масса изделия, кг.

Тогда

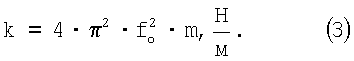
Так как

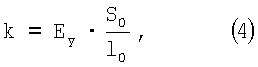
где Е_y – модуль нормальной упругости, МПа, характеризующий жесткость материала, которая связана с силами межатомного взаимодействия;

S₀ – площадь поперечного сечения, м²;

l₀ – длина, м.

Тогда

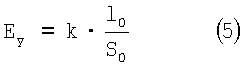
Выразив f₀ через модуль нормальной упругости:

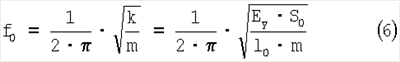
получим, что

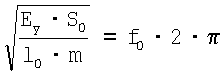
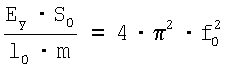
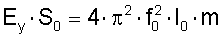
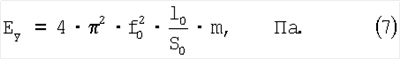
Скорость звука:

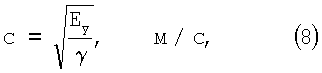
где – удельная плотность материала, кг/м³,

где

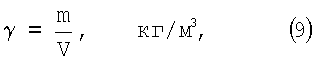
Возведя обе части уравнения (8) в квадрат, получим:

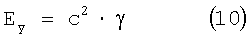
Тогда связь между скоростью звука и резонансной частотой:

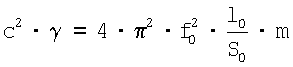
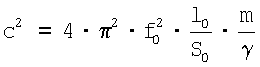
Так как

,

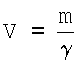то

То есть

Тогда

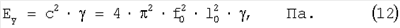
Таким образом, последнее выражение показывает связь между модулем нормальной упругости и резонансной частотой.

При ударе по образцу материала потенциальная энергия вначале убывает, а затем из-за релаксационности процесса вновь возрастает. Резонансная частота выявляется с помощью вэйвлетпреобразования:

,

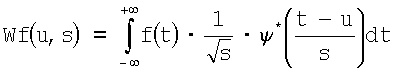где 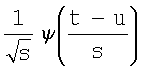– вэйвлет с параметром растяжения – S и прараметром сдвига u.

Так как имеется фиксированное во времени начало отсчета, то используется аналитический вэйвлет:

,

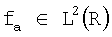где L²(R) – функция конечной энергии – .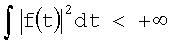

Так как модуль сдвига (модуль касательной упругости) это есть отношение касательного напряжения к углу сдвига (относительному сдвигу):

то резонансная частота f_кр возникает при касательной ударной нагрузке, наносимой по изделию.

Тогда, учитывая выражения (11) и (12), касательная скорость звука определится как:

а модуль сдвига:

где f_КР – резонансная частота, возникающая при касательной ударной нагрузке, Гц;

l₀ – длина, м;

– удельная плотность материала, кг/м³.

Таким образом, показана связь между модулем сдвига и резонансной частотой при касательной нагрузке.

Важным параметром упругих свойств материалов является коэффициент Пуассона , определяющийся как отношение относительной поперечной деформации к относительной продольной деформации. Коэффициент Пуассона характеризует стремление материала сохранять свой первоначальный объем в процессе упругой деформации.

По модулю нормальной упругости Е и модулю касательной упругости G коэффициент Пуассона определяется как:

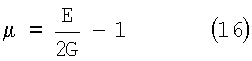
С учетом выше приведенных выражений для нормального и касательного модуля упругости, выраженных через резонансные частоты, коэффициент Пуассона можно определить как:

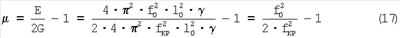
То есть

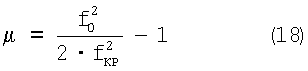
Еще Герц предложил, что:

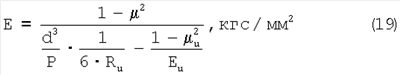
где

– коэффициент Пуассона материала;

_и – коэффициент Пуассона индентора;

d – диаметр лунки от контакта индентора, мм;

Р – нагрузка на шар, кгс;

Е_и – модуль нормальной упругости индентора, кгс/мм²;

R_и – радиус кривизны рабочей части индентора, мм.

При известных , _и, Е_и, R_и, Р и Е можно определить диаметр лунки от контакта индентора:

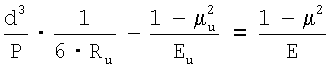
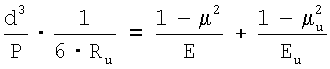
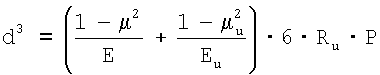
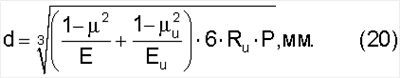
Учитывая требования ГОСТ 9012-59, твердость по Бринеллю соответствует размерности кгс/мм², вместо которой ставится НВ, поэтому Е и Е_и целесообразно перевести в кгс/мм², а Р – в кгс.

Подставляя для и Е ранее полученные выражения, выраженные через резонансные частоты, определим диаметр лунки от контакта индентора как

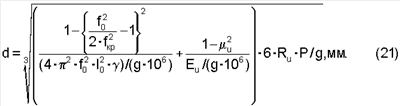
В этом выражении Е_и выражено в Па, а Р – в Н, R_и – в мм.

Глубина невосстановленной лунки по данным Марковца М.П., то есть глубина лунки, когда шаровой индентор находится в ней под нагрузкой, определяется на основании геометрических соотношений:

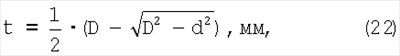
где D – диаметр шара индентора, мм.

Площадь шарового сегмента М, соответствующего диаметру лунки d определится как:

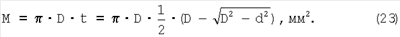
Тогда твердость по Бринеллю:

С учетом d, выраженного ранее через резонансные частоты, твердость по Бринеллю определится как:

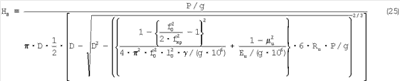
Так как при волновом способе вдавливание реально не проводится, то далее будем называть такой индентор условным.

Учитывая постоянство данных условного индентора:

сферический стальной индентор с радиусом закругления

R_и=5 мм;

коэффициент Пуассона индентора _и=0.285;

модуль нормальной упругости индентора Е_и=221000, МПа;

диаметр D=10 мм;

нагрузка Р=29400 Н,

твердость по Бринеллю определится как:

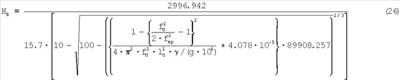
Таким образом, показана связь твердости по Бринеллю с резонансными частотами.

Связь временного сопротивления _В с твердостью по Бринеллю НВ для большинства случаев описывается уравнением:

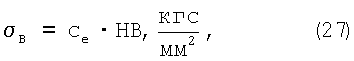
где с_е – экспериментальный коэффициент, зависящий от материала.

Исходя из выражения (27) и с учетом ранее выведенных выражений определения твердости по Бринеллю по резонансным частотам следует, что

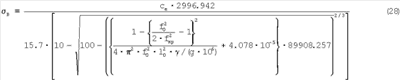
Для перехода в систему СИ

Для ряда материалов экспериментальный коэффициент с_е определяется по выражению:

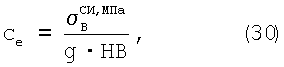
где 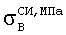– временное сопротивление, выраженное в МПа.

Средняя степень деформации поверхностного слоя лунки при вдавливании шара в плоскость (по Марковцу М.П.):

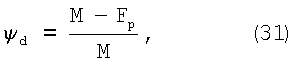
где М=·D_S·t – площадь шарового сегмента М, соответствующего диаметру лунки d, мм²;

D_S=10 мм – диаметр шара индентора;

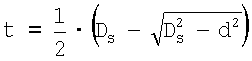, глубина невосстановленной лунки, то есть глубина лунки, когда шаровой индентор находится в ней под нагрузкой, мм;

d – диаметр лунки, мм;

диаметр лунки, выраженный через резонансные частоты равен:

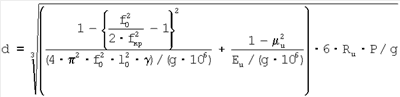
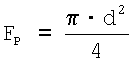– площадь проекции восстановленной лунки, мм.

То есть глубина лунки, когда шаровой индентор находится в ней под нагрузкой, мм:

а площадь проекции восстановленной лунки, мм²:

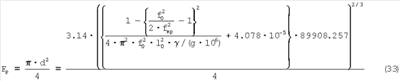
Таким образом, получены выражения для определения средней степени деформации поверхностного слоя лунки при условном вдавливании шара в плоскость.

По отношению диаметра лунки (d) к диаметру шара (D_s) можно (по Марковцу М.П.) графически определить деформацию в невосстановленной лунке (_H) для конструкционных материалов, совпадающей с значением деформации при растяжении, то есть с относительным сужением ().

Выразим отношение диаметра лунки к диаметру шара через диаметральный коэффициент:

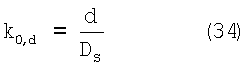
Тогда диаметральный коэффициент определится через резонансные частоты, как:

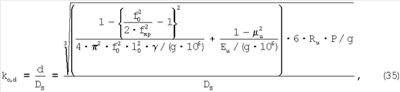
а при D_s=10 мм

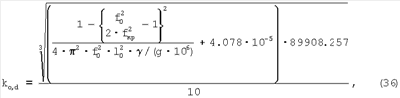
что позволяет определять относительное сужение по резонансным частотам.

Таким образом, получено выражение для определения относительного сужения через резонансные частоты.

Относительное удлинение определяется как:

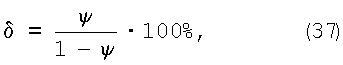
Так как выражение (37) использует относительное сужение, выраженное не в процентах, надо разделить на 100 относительное сужение, выраженное в процентах, и подставить результат в выражение (37).

Таким образом,

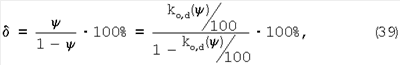
Это выражение является расчетным для определения относительного удлинения через резонансные частоты.

Среднее напряжение в лунке по Мейеру определяется как:

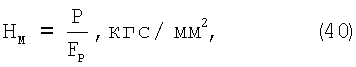
где Р – нагрузка на шар, кгс;

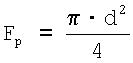– площадь проекции восстановленной лунки, мм;

d – диаметр лунки, мм;

диаметр лунки, выраженный через резонансные частоты, равен:

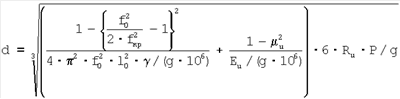
При P=29400/g, кгс

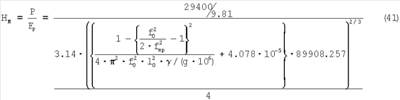
Это выражение является расчетным для определения среднего напряжения в лунке по Мейеру по резонансным частотам.

Так как при идентичных деформациях в лунке и при растяжении напряжение в лунке Н_В связано с условным напряжением при растяжении через коэффициент:

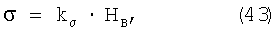
где k – эмпирический коэффициент,

а истинное напряжение при разрыве S связано с условным напряжением как:

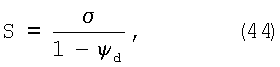
то

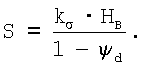
Учитывая, что 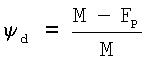и проведя преобразования получим, что S=k·Н_м.

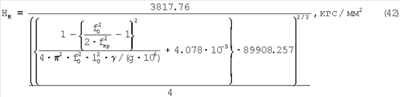
С учетом выражения (42)

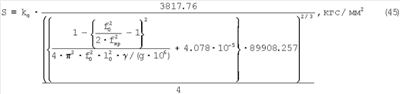
Для перехода в систему СИ:

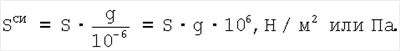
Это выражение позволяет определять истинное напряжение при разрыве по резонансным частотам.

Независимо от наличия площадки текучести, можно определить условный предел текучести.

Для контроля величины твердости Н_0.2 (по Марковцу М.П.) необходимо вдавливать шар диаметром 10 мм до момента, когда диаметр остаточного отпечатка становится равным 0.9 мм. По измеренной в этот момент нагрузке определяется значение Н_0.2.

Из выражения (21) для диаметра лунки от контакта индентора, приведенного для контроля твердости по Бринеллю волновым методом, следует, что:

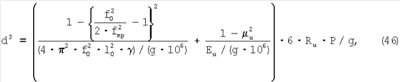
выразим нагрузку, кгс:

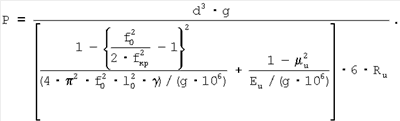
Учитывая, что диаметр остаточного отпечатка равен 0.9 мм:

d=0,9 мм,

a R_и=5 мм,

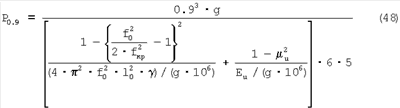
Поделим полученную нагрузку Р_0,9 на площадь поверхности невосстановленной лунки, которая (по Марковцу М.П.) равна 0.636 мм, и получим твердость на пределе текучести:

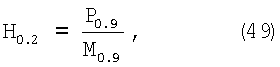
где 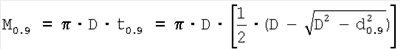– площадь шарового сегмента, мм²;

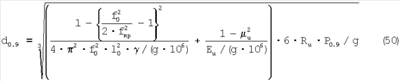
– диаметр лунки, мм

То есть нагрузка

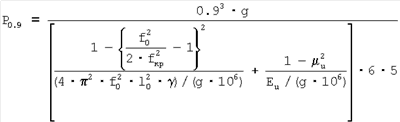
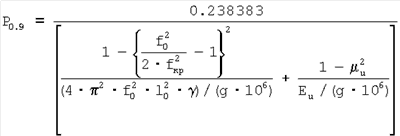
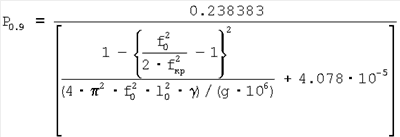
Определив твердость на пределе текучести по выражению (49), определяется предел текучести для стальных материалов по (Марковцу М.П.) как:

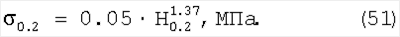
Для различных иных материалов есть универсальная зависимость Марковца М.П.:

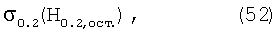
где:

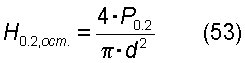
– твердость на пределе текучести по остаточной деформации 0.2% в восстановленной лунке,

Р_0.2 – нагрузка, соответствующая остаточной деформации в лунке 0.2%;

d=0.95 мм – диаметр восстановленной лунки при остаточной деформации 2%.

Тогда нагрузка, соответствующая остаточной деформации в лунке 0.2%, определится как:

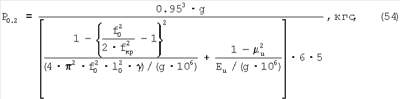
а твердость на пределе текучести по остаточной деформации 0.2% в восстановленной лунке:

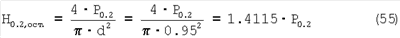
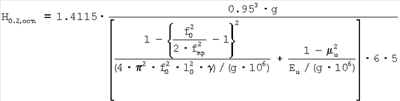
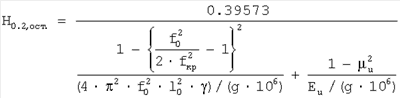
Полученное выражение позволяет определить твердость на пределе текучести по остаточной деформации 0.2% в восстановленной лунке по резонансным частотам.

Предел текучести определится как:

где k_0.2 – коэффициент, зависящий от материала и учитывающий переход из кгс/мм² в МПа.

Если это выражение выразить через резонансные частоты, то получим:

Последнее выражение позволяет определять предел текучести по резонансным частотам.

Ударная вязкость является показателем оценки склонности материала к хрупкости. Ударная вязкость определяется стационарно через испытания призматических надрезанных образцов на маятниковых копрах. Ударную вязкость КС оценивают величиной полной работы К, затраченной на ударный излом образца и отнесенной к площади поперечного сечения образца в надрезе F_н, то есть:

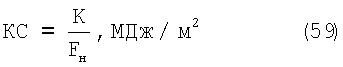
По методу Дроздовского Б.А. испытывают ударные образцы с V-образным надрезом. В этом случае ударная вязкость обозначается как KCV.

По методу Гуляева А.П. испытывают несколько ударных образцов с различным радиусом закругления в вершине надреза. Ударная вязкость обозначается в этом случае как KCU.

Ударная вязкость зависит от объема, вовлекаемого в пластическую деформацию в месте надреза. Деформируемый объем зависит от упрочняемости металла, которая может быть охарактеризована равномерной деформацией при растяжении или отношением .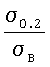

Так как существует связь предела текучести _0,2 с Н_0,2 и предела прочности _в с НВ, то можно оценивать ударную вязкость по 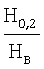с учетом величины зерна (по Матюнину В.М.), так как размер зерна влияет на величину ударной вязкости: чем больше зерно, тем ниже ударная вязкость.

Есть зависимость работы растяжения: _в·l_с.y., с ударной вязкостью, где l_с.y. – среднее удлинение образца при максимальной нагрузке.

Среднее удлинение образца при максимальной нагрузке учитывается относительным удлинением . Следовательно, между условной работой растяжения:

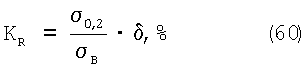
и ударной вязкостью существует зависимость: К_R (КС).

Условная работа растяжения может быть выражена через резонансные частоты как:

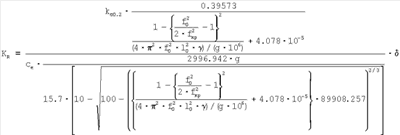
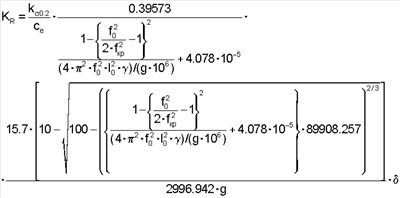
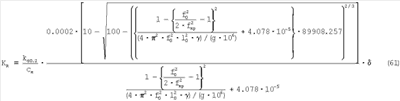
что позволяет определить ударную вязкость материалов по эмпирическим графикам.

Таким образом, через расчетное выражение для определения условной работы растяжения, выраженной через резонансные частоты, можно определить ударную вязкость.

Процесс усталости представляет собой сумму накладывающихся частично друг на друга состояний – упругое, пластическое и разрушение. Из тех же составных частей состоит и процесс однократного нагружения. Усталостная трещина так же, как и трещина при однократном нагружении, происходит из поверхностей пластических сдвигов. Сам механизм разрушения при однократном и многократном нагружении приближенно считают одинаковым. Более низкую прочность при повторном нагружении по сравнению с однократным объясняют тем, что при многократном нагружении сдвиги и пластические деформации сосредотачиваются лишь в отдельных малых объемах образца, тогда как при однократном нагружении сдвиги распространяются на весь рабочий объем образца. В результате разрушение при многократном нагружении начинается в пластически продеформированных до предела отдельных малых объемах образца при наличии большей части образца, которая подверглась нагружению только в пределах упругих деформаций. При однократном нагружении разрушение может начаться в отдельных малых объемах образца, но только когда остальной объем образца претерпел пластическую деформацию, стремящуюся к предельной. При таком механизме разрушения прочность при многократных нагрузках должна быть меньше, чем при однократном нагружении, вследствие уникальности пластической деформации и разрушения при повторном нагружении.

Разрушению металла от усталости предшествует накопление локальных макросдвигов, появление пластических деформаций местного характера, приводящее к местному разрушению.

Причинами разрушения от усталости могут быть мелкие поры, неметаллические включения (металлургические причины), а также неровности поверхности, шероховатости от механической обработки (технологические причины) или резкие переходы от одного сечения к другому (конструкционные причины).

Усталость может появиться при первом циклическом нагружении, если оно выходит за пределы упругости.

При повторных нагружениях в тех объемах, в которых при первом нагружении напряжения достигают предела упругости, запас пластичности постепенно уменьшается и наступает момент разрушения.

Усталостное явление зависит от уровня предела упругости, равномерной деформации, предельной пластичности наиболее уязвимых объемов металла и от рабочего напряжения.

Формулы Лера, Штрибека, Майлендера и Жукова устанавливают связь между пределом выносливости (_-1) и временным сопротивлением и пределом текучести:

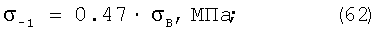
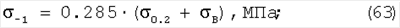
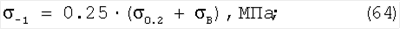
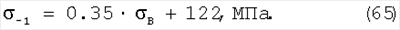
Формулы Юнгера и Леквиса устанавливают связь между пределом выносливости (_-1), временным сопротивлением, пределом текучести и с параметрами пластичности:

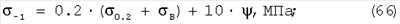
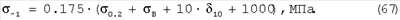
Формулы Герольда, Жукова, Марковца устанавливают связь между пределом выносливости (_-1) с сопротивлением разрушению S_K:

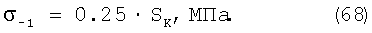
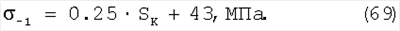
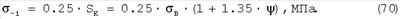
Последнее выражение применяется для _p15%.

Углеродистые, низколегированные стали перлитного класса, алюминиевые сплавы, как правило, имеют такое равномерное поперечное сужение.

Для выражений (68)-(70) ранговый коэффициент корреляции равен 0.93-0.95.

Проведенное исследование показало, что целесообразно определять предел выносливости (_-1) как среднеарифметическое суммы формулы Герольда и формулы Жукова, так как наибольшее число результатов контроля, совпадающих с пределом выносливости, определенным стационарным способом, попадают в область между этими двумя формулами.

Таким образом, определим предел выносливости как:

Проведя некоторые преобразования и выразив это выражение через резонансные частоты с учетом выражения (45) получим:

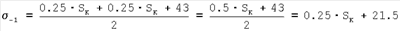
То есть

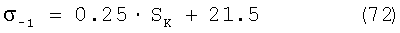
Тогда при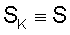

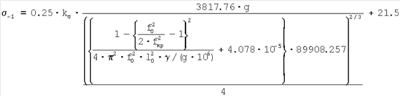
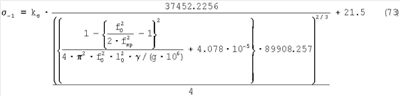
Это выражение позволяет по резонансным частотам определить предел выносливости.

Воздействие на материалы одновременно статического и переменного нагружения приводит к процессу, который можно рассматривать как несимметричный цикл, состоящий из двух напряжений: статического

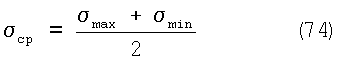
и переменного, симметрично меняющегося по отношению к _ср с амплитудой

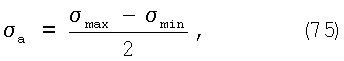
выше которой наступает разрушение материала.

При условии, что предельная амплитуда колебаний напряжений падает по линейному закону, стремясь к нулю при среднем напряжении цикла, равном _0.2, _B и S_K, получим уравнения:

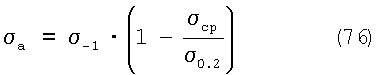
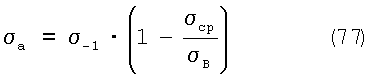
и уравнение Марковца-Савельева-Жильмо:

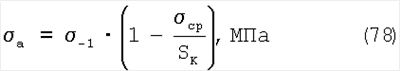
Примем это выражение для определения сопротивления усталости, но выразим его через резонансные частоты. Так как, исходя из выражения (72):

_-1=0.25·S_K+21.5,

то

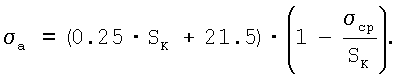
Следовательно,

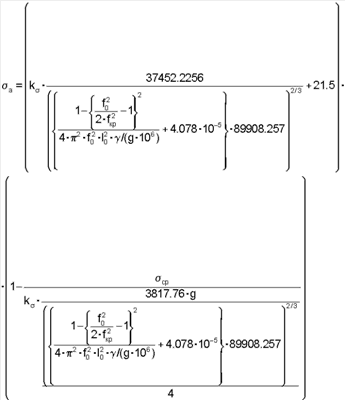
Преобразуем это выражение и получим:

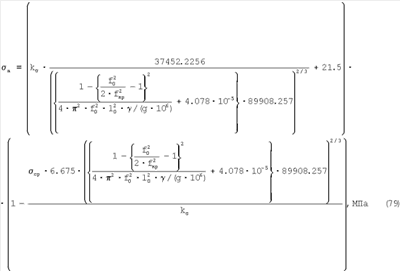
Таким образом, показана связь между сопротивлением усталости и резонансными частотами.

Изложенный способ показывает связь резонансных частот с следующими параметрами материалов /2:43-101/:

1) модуль нормальной упругости, Е_Y, МПа;

2) модуль сдвига, G, МПа;

3) коэффициент Пуассона, ;

4) твердость по Бринеллю, НВ;

5) временное сопротивление, _в, МПа;

6) относительное сужение, , %;

7) относительное удлинение, , %;

8) истинное напряжение при разрыве, S, МПа;

9) предел текучести, _0,2, МПа;

10) ударная вязкость, КС, КДж/м²;

11) предел выносливости, _-1, МПа;

12) сопротивление усталости, _a, МПа.

Признаки характеристики способа.

Необходимо произвести:

– взвесить круглый цилиндрический образец и определить его массу;

– измерить длину и диаметр образца;

– нанести ударным механизмом удар по круглому образцу, закрепленному в держателе только с одной стороны, в двух направлениях – по вертикальной оси сверху (сжимающий удар) и по касательной у нижнего свободного края образца (касательный удар);

– записать на ЭВМ через микрофон, находящийся в 20 см от образца, собственные волны образца материала от двух ударов (две записи);

– полученные записи подвергнуть спектральному анализу;

– выявить из первой записи резонансную частоту от сжимающего удара;

– выявить из второй записи касательную резонансную частоту;

– ввести полученные результаты в ЭВМ;

– провести расчет на ЭВМ по выше приведенным выражениям;

– распечатать результат контроля.

Осуществление изобретения.

Последовательность действий над образцом приведена выше. Контроль проводится при температуре 20°С, нормальном атмосферном давлении и нормальной влажности. Используются следующие средства: датчик фирмы Olympus ME4A (частотный диапазон: 50-8000 Гц; чувствительность – 60 дБ; сопротивление 2.2 кОм; униполярный сигнал на выходе 2-50 мВ);

Диапазон аналогового напряжения (D), которое может оцифровывать приборная система АЦП, определен соответственно до {2-50} мВ.

Ширина кода (минимальное выявляемое изменение аналогового сигнала) определится при 16-битном квантовании как:

. Таким образом, ширина кода составляет 1.5% от максимального значения диапазона аналогового напряжения /2:103-110/.

Были проведены сравнительные испытания материалов статическим способом контроля и волновым в Федеральном космическом агентстве «Научно-производственном центре автоматики и приборостроения им. Академика Н.А.Пилюгина», ОАО «ВИЛС», ОАО «Композит».

Для примера был взят материал АКП (мелкодисперсная смесь порошков алюминиевого сплава САС1-50 и кремния) с удельной плотностью 2643.4 кг/м³.

Модуль нормальной упругости, определенный волновым методом, составил 116215,8 МПа, что совпало с данными стационарных исследований (93400…130600, МПа).

Модуль сдвига составил 7442.6 МПа.

Коэффициент Пуассона составил 2.7.

Твердость по Бринеллю составила 169.4 НВ, что совпало с протоколом механических испытаний этого же материала (165.2…171.6, НВ) с максимальной приведенной погрешностью 0.6% относительного среднего значения.

Временное сопротивление составило 232.7 МПа, что совпало с данными стационарных исследований (211.5…307.9 МПа).

Относительное сужение, определенное волновым методом, составило 0.12%.

Относительное удлинение – 0.136%, что совпало с стационарными данными (0.13…0.30, %).

Истинное напряжение при разрыве составило 581.3 МПа.

Предел текучести – 200.1 МПа, что совпало с стационарными данными (199…301 МПа).

Ударная вязкость составила 70 КДж/м².

Предел выносливости составил 166.8 МПа.

Сопротивление усталости – 138.1 МПа.

Сравнительные испытания волновым способом и статическим показали совпадение результатов по свойствам материала.

Библиографические данные

1. Марковец М.П. Учебное пособие по курсу прочность металлов оборудования атомных электрических станций. – М.: МЭИ, 1979. – 94 с.

2. Микита Г.И. Вычислительные сети, приборы и методы контроля свойств материалов. Допущено Министерством образования и науки Российской Федерации в качестве учебного пособия для студентов высших учебных заведений, обучающихся по направлению подготовки и специальностям группы «Металлургия, машиностроение и материалопереработка». – Москва: ТДР – РУДН, 2006. – 132 с.

3. Кадар Андраш. Оценка технического состояния шатунных подшипников тепловозных дизелей методами вибрационной диагностики: Диссертация на соискание ученой степени кандидата технических наук. – М.: МИИТ, 1993. – 160 с.

Формула изобретения

Волновой способ контроля свойств материалов предназначен для контроля важнейших свойств материалов изделия, которое взвешивают, определяют его массу, измеряют длину и диаметр, наносят ударным механизмом удар по образцу, закрепленному в держателе только с одной стороны, в двух направлениях – по вертикальной оси сверху (сжимающий удар) и по касательной у нижнего свободного края образца (касательный удар), записывают на ЭВМ через микрофон, находящийся в 20 см от образца, собственные волны образца материала от двух ударов (две записи), полученные записи подвергают спектральному анализу, выявляют из первой записи резонансную частоту от сжимающего удара, выявляют из второй записи касательную резонансную частоту, вводят полученные результаты в ЭВМ, проводят расчет на ЭВМ, распечатывают результат контроля, характеризующийся резонансными частотами, связанными с модулем нормальной упругости, модулем сдвига, коэффициентом Пуассона, твердостью по Бринеллю, временным сопротивлением, относительным сужением, относительным удлинением, истинным напряжением при разрыве, пределом текучести, ударной вязкостью, пределом выносливости, сопротивлением усталости.