|
|
(21), (22) Заявка: 2007100864/28, 09.01.2007
(24) Дата начала отсчета срока действия патента:
09.01.2007
(46) Опубликовано: 10.10.2008
(56) Список документов, цитированных в отчете о
поиске:
US 20030229438 А1, 11.12.2003. RU 2183141 С2, 10.06.2002. САНКИН Ю.Н., ТРИФАНОВ А.Е. Осесимметричные колебания оболочек вращения при внезапном нагружении. – ПММ. Том 66, Вып.4, 2002, с.608-616. ТЕУМИН И.И. Ультразвуковые колебательные системы. – М.: Машгиз, 1959.
Адрес для переписки:
432027, г.Ульяновск, ул. Северный Венец, 32, ГОУ ВПО “Ульяновский государственный технический университет”, проректору по научной работе
|
(72) Автор(ы):
Санкин Юрий Николаевич (RU),
Трифанов Андрей Евгеньевич (RU)
(73) Патентообладатель(и):
Государственное образовательное учреждение высшего профессионального образования “Ульяновский государственный технический университет” (RU)
|
(54) СПОСОБ УСИЛЕНИЯ МЕХАНИЧЕСКИХ КОЛЕБАНИЙ ПРИ ПОМОЩИ ВОЛНОВОДА, ВЫПОЛНЕННОГО В ВИДЕ КОНИЧЕСКОЙ ОБОЛОЧКИ ВРАЩЕНИЯ
(57) Реферат:
Изобретение относится к испытательной технике и может быть использовано в приборостроении для создания вибростендов. Способ заключается в следующем. Усиление колебаний реализуется при помощи волновода, выполненного в виде конической оболочки вращения. В качестве волновода используют тонкостенную круговую коническую оболочку. При этом на широкое основание круговой конической оболочки подается высокочастотный сигнал с закрепленного на нем магнитострикционного или электромагнитного устройства. На противоположном конце оболочки получаются усиленные колебания той же частоты. За счет изменения параметров волновода, а именно – угла раствора конуса и толщины оболочки, можно получить требуемое усиление колебаний. Технический результат заключается в возможности реализации усиления и передачи высокочастотных колебаний в диапазоне ультразвука при малой амплитуде возбуждения. 5 ил.
Изобретение относится к способам повышения уровня механических колебаний без наличия редукторов и эксцентриков и может быть использовано в приборостроении для создания вибростендов.
Существует способ создания вибростендов, основанный на возбуждении колебаний упруго-опертой платформы при помощи электромагнитов (см. патент US 2003/0229438 A1 G06F 17/00) и принятое за прототип.
К причинам, препятствующим достижению указанного ниже технического результата при применении известного способа возбуждения колебаний, принятого за прототип, относятся: невозможность усиление и передачи колебаний в диапазоне ультразвука при малой амплитуде возбуждения.
Технический результат – усиление высокочастотных колебаний в диапазоне ультразвука с амплитудой возбуждения порядка нескольких микрометров, создаваемых магнитострикционным или электромагнитным устройством.
Особенность заключается в том, что меняя параметры волновода, а именно угол раствора конуса и толщину оболочки, получаем требуемое усиление колебаний, минуя различные промежуточные устройства.
Уравнения гармонических колебаний оболочки вращения могут быть записаны в виде, см.: Фридман В.М., Чернина B.C. Видоизменение метода Бубнова-Галеркина-Ритца, связанное со смешанным вариационным принципом в теории упругости. – Известия АН СССР, МТТ, №1, 1969, с.64-78:

где хТ=|T1, T2, S, M1, M2, H| – вектор усилий Т1, М1 и Т2, М2 – меридиальные и окружные растягивающие усилия и изгибающие моменты; 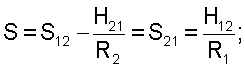 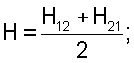 S12, S21, H12, H21 – касательные усилия и крутящие моменты; уT=|u, v, w| – вектор перемещений; u – перемещение по касательной к меридиану, v – перемещение по касательной к параллели; w – нормальное перемещение; fT=|q1, q2, qn| – вектор внешней нагрузки; q1, q2, qn соответствуют по направлению составляющим вектора перемещений; R – масса, приходящаяся на единицу площади срединной поверхности оболочки, S12, S21, H12, H21 – касательные усилия и крутящие моменты; уT=|u, v, w| – вектор перемещений; u – перемещение по касательной к меридиану, v – перемещение по касательной к параллели; w – нормальное перемещение; fT=|q1, q2, qn| – вектор внешней нагрузки; q1, q2, qn соответствуют по направлению составляющим вектора перемещений; R – масса, приходящаяся на единицу площади срединной поверхности оболочки,  – частота вынужденных колебаний, – частота вынужденных колебаний,

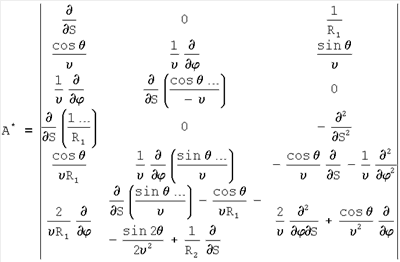
R1, R2 – главные радиусы кривизны;  – радиус кривизны параллели; – радиус кривизны параллели;

В=Eh/(1- 2) – жесткость при растяжении; D=Eh3/12(1- 2) – жесткость при растяжении; D=Eh3/12(1- 2) – цилиндрическая жесткость при изгибе; Е – модуль упругости; 2) – цилиндрическая жесткость при изгибе; Е – модуль упругости;  – коэффициент Пуассона; h – толщина оболочки. Операторы А и А* обладают свойством: – коэффициент Пуассона; h – толщина оболочки. Операторы А и А* обладают свойством:
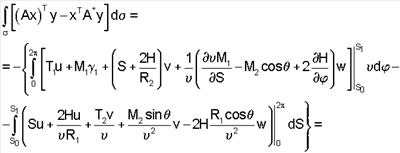
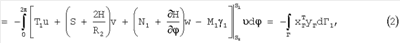
где  – поверхность оболочки. При вычислении интеграла (2) учтена периодичность по углу – поверхность оболочки. При вычислении интеграла (2) учтена периодичность по углу  . Здесь . Здесь 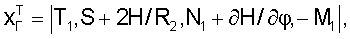 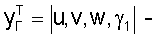 соответственно векторы обобщенных сил и перемещений на краях элемента, структура операторов А и А* дана в работах. Уравнения (1) следует дополнить соответствующими граничными условиями, которые следуют из свойств операторов (2), соответственно векторы обобщенных сил и перемещений на краях элемента, структура операторов А и А* дана в работах. Уравнения (1) следует дополнить соответствующими граничными условиями, которые следуют из свойств операторов (2),

Здесь Г1 – часть контура, где заданы усилия; Г2 – часть контура, где заданы перемещения. Деление граничного контура на Г1, Г2 считается условным, так как на одном и том же участке могут быть заданы отдельные компоненты вектора обобщенных сил и дополнительные компоненты вектора перемещений.
Решение таким образом поставленной задачи сообщает функционалу
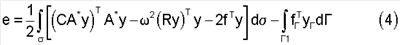
стационарное значение.
Второй интеграл в выражении функционала (4) является работой граничных усилий и конструируется согласно (2).
Для конической оболочки (Фиг.1), когда R1= , при осесимметричной нагрузке величина, связанная с перемещением v, не рассматривается, а операторы А* и С преобразуются к виду: , при осесимметричной нагрузке величина, связанная с перемещением v, не рассматривается, а операторы А* и С преобразуются к виду:
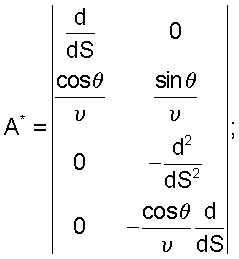 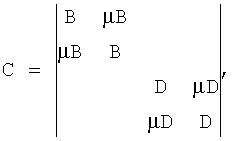
где dS= d d . .
Зададимся полем перемещений в виде: u= 1+ 1+ 2S, w= 2S, w= 3S+ 3S+ 4S+ 4S+ 5S2+ 5S2+ 6S3, где 6S3, где  1, …, 1, …,  6 – неизвестные коэффициенты. 6 – неизвестные коэффициенты.
Такое представление может быть оправдано тем, что, например, для цилиндрической оболочки уравнение изгиба не связано с уравнением растяжения и эта зависимость мала при относительно малых  и малой длине элемента. Найдем функции формы. Функции формы определяются согласно соотношению U=NUij, где и малой длине элемента. Найдем функции формы. Функции формы определяются согласно соотношению U=NUij, где 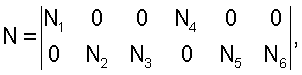 UT=|u w|, UT=|u w|, 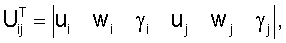 ui, wi, ui, wi,  i, uj, wj, i, uj, wj,  j – перемещения и углы поворота краевых сечений. N1, …, N6 – функции формы. j – перемещения и углы поворота краевых сечений. N1, …, N6 – функции формы.
Введем переменную 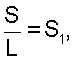 где L – длина элемента по образующей. Тогда получим [5]: где L – длина элемента по образующей. Тогда получим [5]: 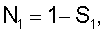 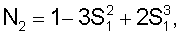 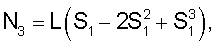 N4=S1, N4=S1, 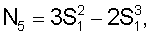 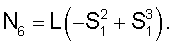
При переходе от местной системы осей 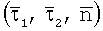 к единой (X, Y, Z), выражая вектор у через матрицу функций формы N и узловые перемещения к единой (X, Y, Z), выражая вектор у через матрицу функций формы N и узловые перемещения
zТ=|ui, wi, dwi/dS, Uj, wj, dwj/dS|,
функционал (4) перепишется в виде:
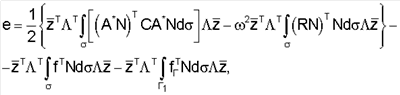
где
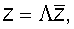 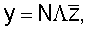 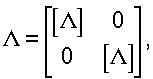 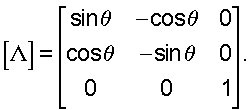
Учитывая, что d =2 =2 LdS, получим для матриц жесткостей и масс следующие выражения: LdS, получим для матриц жесткостей и масс следующие выражения:
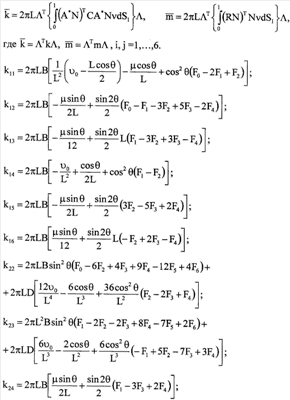 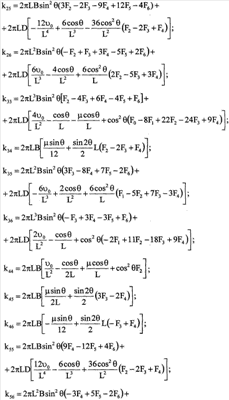 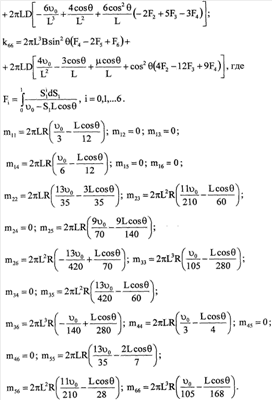
Для формирования глобальной матрицы представим матрицу жесткости и матрицу разбитой на блоки 3×3:
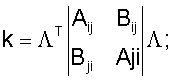 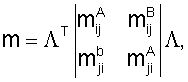
а вектор нагрузки fТ=|fij, fji|. Тогда для оболочки получим следующее рекуррентное соотношение, подобное аналогичному соотношению для балок:
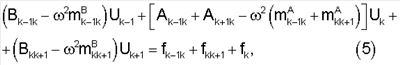
где k – номер характерного сечения, fk – вектор нагрузки в сечении k.
Для того чтобы учесть рассеяние энергии, подставим вместо Е величину E(1+i ) в уравнения (5), где ) в уравнения (5), где  – коэффициент внутреннего рассеяния энергии, и решая систему уравнений (5), строим амплитудно-фазочастотные характеристики АФЧХ (Фиг.2). Математическая, модель оболочки вращения формируется по характерным точкам АФЧХ в виде: – коэффициент внутреннего рассеяния энергии, и решая систему уравнений (5), строим амплитудно-фазочастотные характеристики АФЧХ (Фиг.2). Математическая, модель оболочки вращения формируется по характерным точкам АФЧХ в виде:

где kj=AjT1j/T2j – коэффициент усиления j-ого колебательного звена; Аj – вертикальный размер витка АФЧХ; Т1j=T2j(1- 2 2j/ 2 2j/ 2 1j) – постоянная времени демпфирования; Т2j=1/ 2 1j) – постоянная времени демпфирования; Т2j=1/ 1j – инерционная постоянная; 1j – инерционная постоянная;  1j – резонансная частота, соответствующая максимуму мнимой части АФЧХ; 1j – резонансная частота, соответствующая максимуму мнимой части АФЧХ;
 2j – частота, соответствующая максимуму действительной части АФЧХ; 2j – частота, соответствующая максимуму действительной части АФЧХ;
 – частота колебаний; i – мнимая единица, – частота колебаний; i – мнимая единица,
после чего определяется частота возбудителя магнитострикционных или электромагнитных колебаний, обеспечивающая на выходе максимальную амплитуду усиливаемых колебаний.
Формула (6) получена в работе Санкин Ю.Н. Динамические характеристики вязкоупругих систем с распределенными параметрами. Саратов, изд-во СГУ, 1977, 309 с. Формулы для Т1j и T2j приведены в работе Санкин Ю.Н. Малые колебания механических систем с одной степенью свободы. Ульяновск, изд во УлГТУ, 1991, 36 с.
Известен волновод, выполненный в виде конического стержня сплошного сечения. Недостатком, препятствующим выполнению поставленной задачи, является значительная погонная масса стержня, малая площадь сечения, к которому прикладывается возмущающее воздействие, что существенно ограничивает мощность передаваемого сигнала, а также наличие больших потерь на внутреннее трение, что не позволяет создавать высокочастотные вибростенды, необходимые для проверки работоспособности оборудования в условиях мощного высокочастотного звукового поля.
Способ усиления механических колебаний при помощи волновода, выполненного в виде конической оболочки вращения, отличается тем, что в качестве волновода используют тонкостенную круговую коническую оболочку, на широкое основание которой подают высокочастотный сигнал с закрепленного на ней магнитострикционного или электромагнитного генератора механический колебаний, причем частоту возбуждения выбирают при помощи математической модели поведения оболочки на выходе, определяемой по формуле (6) на частоте  , когда амплитуда колебаний на выходе оказывается максимальной. Предлагаемая конструкция свободна от вышеуказанных недостатков, т.к. радиус сечения оболочки, где прикладывается возмущающее воздействие, может быть выбран достаточно больших размеров в зависимости от величины передаваемой мощности. Также из соображений минимизации потерь на внутреннее трение устанавливается толщина оболочки (Фиг.3), где 1 – приборный отсек, 2 – коническая оболочка, 3 – вибратор, выполненный из магнитострикционного материала, 4 – катушка для возбуждения колебаний, ЗГ – звуковой генератор. , когда амплитуда колебаний на выходе оказывается максимальной. Предлагаемая конструкция свободна от вышеуказанных недостатков, т.к. радиус сечения оболочки, где прикладывается возмущающее воздействие, может быть выбран достаточно больших размеров в зависимости от величины передаваемой мощности. Также из соображений минимизации потерь на внутреннее трение устанавливается толщина оболочки (Фиг.3), где 1 – приборный отсек, 2 – коническая оболочка, 3 – вибратор, выполненный из магнитострикционного материала, 4 – катушка для возбуждения колебаний, ЗГ – звуковой генератор.
Ниже приводится зависимость выходного сигнала от радиуса входного сечения (Фиг.4), где сплошной линией показан выходной сигнал конической оболочки радиуса 0.25 м и толщиной 5 мм, а пунктирной – радиуса 0.5 м и толщиной 5 мм, и изменение амплитуды в зависимости от толщины стенки (Фиг.5), определяющей потери на внутреннее трение, где сплошной линией показан выходной сигнал конической оболочки радиуса 0.5 м и толщиной 2 мм, а пунктирной – радиуса 0.5 м и толщиной 5 мм.
Формула изобретения
Способ усиления механических колебаний при помощи волновода, выполненного в виде конической оболочки вращения, отличающийся тем, что в качестве волновода используют тонкостенную круговую коническую оболочку, на широкое основание которой подают высокочастотный сигнал с закрепленного на ней магнитострикционного или электромагнитного генератора механических колебаний, меняя параметры волновода, а именно угол раствора конуса и толщину оболочки, получают требуемое усиление колебаний, минуя различные промежуточные устройства, причем частоту возбуждения выбирают при помощи математической модели поведения оболочки на выходе, определяемой по формуле
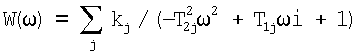 , ,
где kj=AjT1j/T2j – коэффициент усиления j-ого колебательного звена;
Аj – вертикальный размер витка АФЧХ;
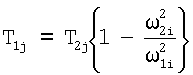 – постоянная времени демпфирования; – постоянная времени демпфирования;
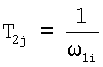 – инерционная постоянная; – инерционная постоянная;
 1j – резонансная частота, соответствующая максимуму мнимой части АФЧХ; 1j – резонансная частота, соответствующая максимуму мнимой части АФЧХ;
 2j – частота, соответствующая максимуму действительной части АФЧХ; 2j – частота, соответствующая максимуму действительной части АФЧХ;
 – частота колебаний; – частота колебаний;
i – мнимая единица,
на частоте  , когда амплитуда колебаний на выходе оказывается , когда амплитуда колебаний на выходе оказывается
максимальной.
РИСУНКИ
MM4A – Досрочное прекращение действия патента СССР или патента Российской Федерации на изобретение из-за неуплаты в установленный срок пошлины за поддержание патента в силе
Дата прекращения действия патента: 10.01.2009
Извещение опубликовано: 20.06.2010 БИ: 17/2010
|
|