|
(21), (22) Заявка: 2006137979/11, 24.10.2006
(24) Дата начала отсчета срока действия патента:
24.10.2006
(46) Опубликовано: 27.08.2008
(56) Список документов, цитированных в отчете о
поиске:
RU 2191146 С2, 20.10.2002. RU 2159201 С2, 20.11.2000. RU 2088494 С1, 27.08.1997. SU 1819829 А, 07.06.1993. US 5312073 А, 17.05.1994. GB 1285919 А, 16.08.1972.
Адрес для переписки:
197110, Санкт-Петербург, ул. Б. Зеленина, 2/42, кв.2, А.А.Тихонову
|
(72) Автор(ы):
Антипов Кирилл Андреевич (RU),
Тихонов Алексей Александрович (RU)
(73) Патентообладатель(и):
Антипов Кирилл Андреевич (RU),
Тихонов Алексей Александрович (RU)
|
(54) СПОСОБ ПОЛУПАССИВНОЙ ТРЕХОСНОЙ СТАБИЛИЗАЦИИ ДИНАМИЧЕСКИ СИММЕТРИЧНОГО ИСКУССТВЕННОГО СПУТНИКА ЗЕМЛИ
(57) Реферат:
Изобретение относится к космической технике и может применяться для стабилизации искусственных спутников Земли (ИСЗ) с использованием геомагнитного поля. Согласно предлагаемому способу на части поверхности ИСЗ распределяют двойной электростатический слой. При взаимодействии этого слоя с магнитным полем Земли, вследствие орбитального движения ИСЗ, возникает управляющий момент лоренцевых сил. Данный момент практически может превосходить гравитационный момент, действующий на крупный ИСЗ с динамической симметрией, близкой к полной, либо на гравитационно-ориентированный ИСЗ. Для управления ориентацией ИСЗ с осевой динамической симметрией в орбитальной системе координат изменяют величину и направление вектора дипольного момента двойного слоя в соответствии с проекциями скоростей центра масс ИСЗ и вектора геомагнитной индукции на оси орбитальной системы координат. Полученный закон изменения указанного вектора решает задачу стабилизации ИСЗ вблизи положения равновесия, в котором ось динамической симметрии ИСЗ направлена по местной вертикали. При наличии демпфирования данная ориентация ИСЗ устойчива при действии гравитационных и иных малых возмущений. Технический результат изобретения заключается в расширении области применимости способа управления ориентацией ИСЗ. 5 ил.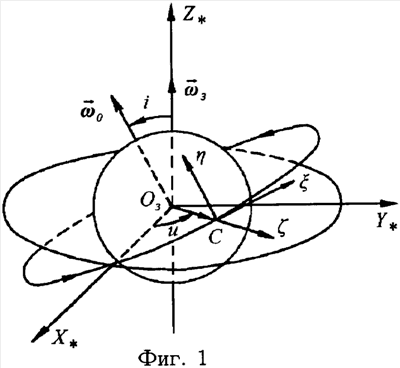
Изобретение относится к области космической техники и может быть использовано для стабилизации искусственных спутников Земли (ИСЗ) путем создания управляемого момента лоренцевых сил.
Известны способы управления ориентацией ИСЗ путем использования различных по своей природе сил – реактивных или внешних по отношению к ИСЗ сил, создающих управляющие моменты. Внешние по отношению к ИСЗ факторы, создающие управляющие моменты без расхода рабочего тела, используются в пассивных способах стабилизации /1/. Использование пассивных способов управления ориентацией ИСЗ предпочтительно в тех случаях, когда во время активной фазы полета отклонение ИСЗ от заданного положения в пространстве не должно превышать нескольких градусов, а также когда не требуется выполнения сложных программных разворотов и противодействия большим возмущающим моментам /2/.
Известны способы и устройства пассивной ориентации (стабилизации) ИСЗ, основанные на использовании природных геофизических факторов, например, гравитационных сил, сил взаимодействия магнитного поля ИСЗ с внешним магнитным полем Земли (МПЗ), давления солнечного излучения, аэродинамических сил. Однако известные способы характеризуются малой эффективностью либо вследствие того, что создание управляющего (стабилизирующего) момента требует значительных конструктивных усложнений, либо вследствие того, что область их практического применения достаточно сильно ограничена. Так, магнитные системы управления (МСУ), имея значительные габариты, создают малые по величине управляющие моменты и являются мощным источником магнитных полей на борту ИСЗ, что ухудшает рабочие характеристики МСУ и снижает эффективность и помехоустойчивость МСУ /1/. Способы, использующие давление солнечного излучения /3/, могут быть эффективны лишь для ИСЗ, находящихся на высоких орбитах /1/, а соответствующие им устройства /4/ требуют больших рабочих поверхностей. Использование аэродинамических систем, основанных на стабилизирующем воздействии набегающего на ИСЗ потока разреженных слоев атмосферы, ограничено малыми орбитальными высотами и значительным влянием атмосферы на параметры орбиты, что снижает эффективность соответствующих устройств управления ориентацией ИСЗ /5/. Общим недостатком известных способов пассивной стабилизации ИСЗ является сложность изменения управляющего момента и ограниченность использования в связи с невозможностью компенсации эксцентриситетных колебаний, возникающих на эллиптических орбитах.
Известен способ управления ориентацией ИСЗ /6/, включающий получение управляемого крутящего момента лоренцевых сил путем распределения на части поверхности ИСЗ двойного электростатического слоя с заданным суммарным дипольным моментом  двойного слоя. При этом получение управляемого крутящего момента производят путем согласованного изменения величины и направления вектора двойного слоя. При этом получение управляемого крутящего момента производят путем согласованного изменения величины и направления вектора  . .
Недостатки известного способа заключаются в следующем. Способ применим для стабилизации ИСЗ только в прямом положении равновесия в орбитальной системе координат. Способ не работает для ИСЗ, находящихся на орбитах с наклонениями, большими 60°.
Известный способ выбран в качестве наиболее близкого аналога к заявляемому изобретению.
Задача изобретения заключается в расширении области применимости способа управления ориентацией ИСЗ.
Задача решена тем, что в известном способе управления ориентацией ИСЗ, включающем получение управляемого крутящего момента лоренцевых сил, в соответствии с изобретением на части поверхности ИСЗ распределяют двойной электростатический слой с заданным суммарным дипольным моментом  двойного слоя, а получение управляемого крутящего момента производят путем согласованного изменения величины и направления вектора двойного слоя, а получение управляемого крутящего момента производят путем согласованного изменения величины и направления вектора  , удовлетворяющего условиям , удовлетворяющего условиям

где Px, Py, Pz – проекции вектора 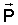 на главные центральные оси инерции ИСЗ, на главные центральные оси инерции ИСЗ,  C C , ,  C C – проекции вектора – проекции вектора 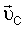 скорости центра масс ИСЗ относительно геомагнитного поля на оси орбитальной системы координат, BC скорости центра масс ИСЗ относительно геомагнитного поля на оси орбитальной системы координат, BC , BC , BC , BC , BC – проекции вектора – проекции вектора  индукции геомагнитного поля в центре масс ИСЗ на оси орбитальной системы координат, индукции геомагнитного поля в центре масс ИСЗ на оси орбитальной системы координат,  0 – угол поворота ИСЗ относительно оси, совпадающей в режиме ориентированного движения с местной вертикалью, k – постоянный коэффициент. 0 – угол поворота ИСЗ относительно оси, совпадающей в режиме ориентированного движения с местной вертикалью, k – постоянный коэффициент.
Технический результат, достигаемый изобретением, состоит в том, что создание двойного электростатического слоя на поверхности ИСЗ приводит к возбуждению сил Лоренца, воздействующих на ИСЗ и оказывающих ориентирующее действие, а выполнение условий на согласованное изменение распределения поляризации обеспечивает существование и устойчивость положения равновесия и при наличии демпфирования (обеспечиваемого каким-либо из известных способов, например, путем использования гистерезисных стержней) решает задачу стабилизации ИСЗ в орбитальной системе координат.
Сущность изобретения поясняется Фиг.1, на которой представлена орбитальная система координат, являющаяся базовой системой при решении задачи стабилизации ИСЗ, Фиг.2, на которой представлены углы ориентации ИСЗ в орбитальной системе координат, Фиг.3, на которой представлены максимальные возможные значения модуля вектора дипольного момента двойного слоя, Фиг.4, 5, на которых представлены результаты численного расчета процесса стабилизации ИСЗ в соответствии с изобретением и без него.
Сущность изобретения заключается в следующем. Для ИСЗ, центр масс которого (точка С) движется со скоростью 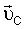 относительно МПЗ, характеризуемого магнитной индукцией относительно МПЗ, характеризуемого магнитной индукцией  распределение на части поверхности ИСЗ с площадью S (далее – оболочка) двойного электростатического слоя с плотностью поляризации распределение на части поверхности ИСЗ с площадью S (далее – оболочка) двойного электростатического слоя с плотностью поляризации 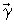 приводит к возникновению момента приводит к возникновению момента 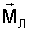 лоренцевых сил, определяемого по формуле лоренцевых сил, определяемого по формуле

где  – суммарный дипольный момент оболочки, оказывающего при определенных условиях ориентирующее воздействие на ИСЗ и используемого в качестве восстанавливающего момента. – суммарный дипольный момент оболочки, оказывающего при определенных условиях ориентирующее воздействие на ИСЗ и используемого в качестве восстанавливающего момента.
Для получения восстанавливающего момента, превышающего действующие возмущающие моменты, можно варьировать параметры двойного электростатического слоя. Оценки показывают, что для характерных величин параметров орбиты ИСЗ R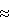 7·106 м, площади двойного электростатического слоя S 7·106 м, площади двойного электростатического слоя S 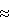 300 м2, напряженности Е электростатического поля в системе электродов, создающих этот двойной слой Е 300 м2, напряженности Е электростатического поля в системе электродов, создающих этот двойной слой Е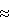 107 В/м, и толщины двойного электростатического слоя d 107 В/м, и толщины двойного электростатического слоя d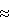 0,05 м момент лоренцевых сил, создаваемый электростатическим слоем, будет величиной порядка 10-4 Н·м, что превосходит момент гравитационных сил, действующих на крупный ИСЗ со сбалансированным распределением масс, или на ИСЗ, предварительно приведенный в положение, близкое к положению гравитационной ориентации. 0,05 м момент лоренцевых сил, создаваемый электростатическим слоем, будет величиной порядка 10-4 Н·м, что превосходит момент гравитационных сил, действующих на крупный ИСЗ со сбалансированным распределением масс, или на ИСЗ, предварительно приведенный в положение, близкое к положению гравитационной ориентации.
Для определения условий, при которых достигается режим стабилизированного движения ИСЗ, рассмотрим ИСЗ, центр масс которого движется в гравитационном поле по круговой кеплеровой орбите. Предполагается, что гравитационное поле Земли является ньютоновским центральным. МПЗ аппроксимируется с учетом дипольной и квадрупольной составляющих /8/. Исследуем вращательное движение ИСЗ относительно его центра масс в орбитальной системе координат С   (Фиг.1) с началом в центре масс ИСЗ, ось (Фиг.1) с началом в центре масс ИСЗ, ось 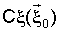 которой направлена по касательной к орбите в сторону движения, ось которой направлена по касательной к орбите в сторону движения, ось 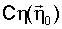 – по нормали к плоскости орбиты, ось – по нормали к плоскости орбиты, ось  – вдоль радиуса-вектора – вдоль радиуса-вектора  центра масс ИСЗ относительно центра Земли ОЗ. Здесь и в дальнейшем используются правые декартовы прямоугольные системы координат. Исследование проводится с учетом вращения орбитальной системы координат относительно инерциальной системы с угловой скоростью центра масс ИСЗ относительно центра Земли ОЗ. Здесь и в дальнейшем используются правые декартовы прямоугольные системы координат. Исследование проводится с учетом вращения орбитальной системы координат относительно инерциальной системы с угловой скоростью  0. В качестве инерциальной системы координат принимается система OЗX*Y*Z*, ось 0. В качестве инерциальной системы координат принимается система OЗX*Y*Z*, ось 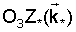 которой направлена по оси собственного вращения Земли, ось которой направлена по оси собственного вращения Земли, ось  – в восходящий узел орбиты, а плоскость (Х*Y*) совпадает с плоскостью экватора. Используется также жестко связанная с ИСЗ система его главных центральных осей инерции Cxyz (орты – в восходящий узел орбиты, а плоскость (Х*Y*) совпадает с плоскостью экватора. Используется также жестко связанная с ИСЗ система его главных центральных осей инерции Cxyz (орты 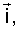  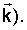 Ориентация орбитальной системы координат относительно системы OЗX*Y*Z* определяется на основании равенств Ориентация орбитальной системы координат относительно системы OЗX*Y*Z* определяется на основании равенств

где 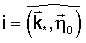 – наклонение орбиты; – наклонение орбиты; 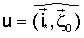 – аргумент широты, u= – аргумент широты, u= 0t. 0t.
Ориентация осей xyz относительно осей    определяется матрицей направляющих косинусов определяется матрицей направляющих косинусов  i, i,  i, i,  i (i=1, 2, 3) так, что имеют место равенства i (i=1, 2, 3) так, что имеют место равенства
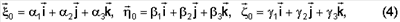
если определять ориентацию ИСЗ в орбитальной системе координат с помощью “самолетных” углов  , ,  , ,  (Фиг.2), то элементы матрицы А примут вид (Фиг.2), то элементы матрицы А примут вид
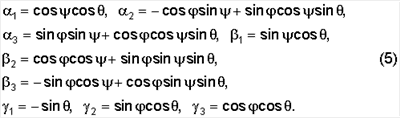
В процессе движения ИСЗ относительно геомагнитного поля взаимодействие двойного электростатического слоя с геомагнитным полем приводит к возбуждению сил Лоренца. Главный момент этих сил относительно центра масс ИСЗ определяется по формуле

В работах /6, 9/ показано, что для любых реальных ИСЗ и тем более для ИСЗ, функционирующих в режимах, близких к ориентированному движению, момент 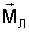 можно аппроксимировать выражением (2), где можно аппроксимировать выражением (2), где
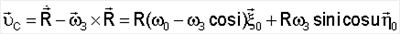 – скорость центра масс ИСЗ относительно геомагнитного поля, – скорость центра масс ИСЗ относительно геомагнитного поля,  – угловая скорость суточного вращения Земли, – угловая скорость суточного вращения Земли, 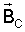 – вектор магнитной индукции геомагнитного поля в центре масс ИСЗ, заданный своими компонентами в орбитальной системе координат. – вектор магнитной индукции геомагнитного поля в центре масс ИСЗ, заданный своими компонентами в орбитальной системе координат.
В условиях квадрупольной модели МПЗ вектор  определяется по формуле определяется по формуле

где  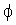 – часовой угол восходящего узла, – часовой угол восходящего узла,
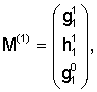  – мультипольные тензоры 1-го и 2-го рангов, представляющие собой соответственно дипольный и квадрупольный магнитные моменты, выраженные через квазинормированные по Шмидту гауссовы коэффициенты – мультипольные тензоры 1-го и 2-го рангов, представляющие собой соответственно дипольный и квадрупольный магнитные моменты, выраженные через квазинормированные по Шмидту гауссовы коэффициенты  и и 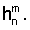 На эпоху 2000.0 гауссовы коэффициенты имеют следующие значения /10/ в нТл: На эпоху 2000.0 гауссовы коэффициенты имеют следующие значения /10/ в нТл:
 
Для нахождения проекций момента 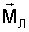 на оси x, y, z представим выражение (2) в виде на оси x, y, z представим выражение (2) в виде

Здесь  С С =R( =R( 0– 0– Зcosi), Зcosi),  С С =R =R Зsin i cos u, Зsin i cos u,  C C =0. =0.
Пусть задана программная ориентация ИСЗ в орбитальной системе координат некоторым значением матрицы направляющих косинусов А=A0=const. В частности, матрица A0 может быть единичной. Этот случай был рассмотрен в /6/. Подставляя А=A0 в выражение (2), найдем такие значения вектора 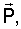 при которых при которых  обращается в ноль в программной ориентации ИСЗ, т.е. является восстанавливающим моментом в окрестности ориентации A0. Очевидно, что вектор обращается в ноль в программной ориентации ИСЗ, т.е. является восстанавливающим моментом в окрестности ориентации A0. Очевидно, что вектор  должен удовлетворять условию должен удовлетворять условию

где k=k(t) – произвольная скалярная функция. При этом компоненты вектора 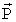 определяются по формулам определяются по формулам

Следовательно, если параметры оболочки Рx, Рy, Рz будут изменяться по закону (8), то момент 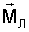 будет являться восстанавливающим в окрестности заданного положения и может быть использован для поддержания заданной ориентации ИСЗ. Равенства (8) можно рассматривать как закон управления вектором дипольного момента оболочки для осуществления заданной ориентации ИСЗ. В зависимости от вида функции k(t) формулы (8) определяют тот или иной закон полупассивного управления ориентацией ИСЗ. будет являться восстанавливающим в окрестности заданного положения и может быть использован для поддержания заданной ориентации ИСЗ. Равенства (8) можно рассматривать как закон управления вектором дипольного момента оболочки для осуществления заданной ориентации ИСЗ. В зависимости от вида функции k(t) формулы (8) определяют тот или иной закон полупассивного управления ориентацией ИСЗ.
Рассмотрим следующий закон полупассивного управления при постоянном значении k. Пусть  – среднее по времени значение – среднее по времени значение 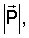 а P0 – некоторое фиксированное значение величины а P0 – некоторое фиксированное значение величины 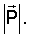 Выберем k исходя из условия Выберем k исходя из условия 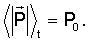 В этом случае на основании (8) получаем В этом случае на основании (8) получаем

где   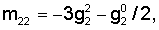 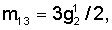  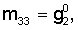 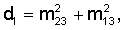  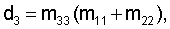 
Для выяснения возможности практической реализации управления (8) целесообразно оценить модули функций Px(t), Py(t) и Pz(t) для наиболее реальных значений параметров ИСЗ и его орбиты.
С помощью ЭВМ выполнены расчеты максимальных по времени значений 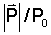 для параметров орбиты из диапазона 0 для параметров орбиты из диапазона 0 i i 90°, 6800 км 90°, 6800 км  R R 13200 км. Результаты расчетов показаны на Фиг.3 для граничных значений радиуса орбиты: кривая 1 соответствует R=6800 км, а кривая 2 – R=13200 км. Промежуточным значениям радиуса соответствуют кривые, заполняющие пространство между кривыми 1 и 2. 13200 км. Результаты расчетов показаны на Фиг.3 для граничных значений радиуса орбиты: кривая 1 соответствует R=6800 км, а кривая 2 – R=13200 км. Промежуточным значениям радиуса соответствуют кривые, заполняющие пространство между кривыми 1 и 2.
Из Фиг.3 видно, что  принимает значения порядка 1 для орбит с произвольными наклонениями и, следовательно, практическая реализация рассматриваемого закона управления не вызовет принципиальных трудностей. принимает значения порядка 1 для орбит с произвольными наклонениями и, следовательно, практическая реализация рассматриваемого закона управления не вызовет принципиальных трудностей.
Докажем, что полупассивное управление (8) при наличии демпфирования в системе ИСЗ решает задачу стабилизации ИСЗ в орбитальной системе координат.
Пусть в системе ИСЗ имеется демпфирующий момент  модельного типа, например пропорциональный относительной угловой скорости ИСЗ в орбитальной системе координат: модельного типа, например пропорциональный относительной угловой скорости ИСЗ в орбитальной системе координат:  где где 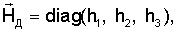 hi>0 (i = 1, 2, 3), hi>0 (i = 1, 2, 3),  а а  – абсолютная угловая скорость ИСЗ. Тогда – абсолютная угловая скорость ИСЗ. Тогда
MДx=-h1( x– x– 0 0 1), MДy=-h2( 1), MДy=-h2( y– y– 0 0 2), MДz=-h3( 2), MДz=-h3( z– z– 0 0 3). 3).
Будем учитывать также гравитационный момент

как наибольший из возмущающих моментов. Здесь J=diag(A, А, С) – тензор инерции ИСЗ в осях Cxyz, причем ось Cz – ось динамической симметрии ИСЗ.
Дифференциальные уравнения вращательного движения ИСЗ строятся по схеме Эйлера-Пуассона:
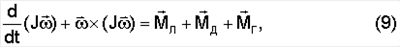

Из уравнений (9), (10) следует, что ИСЗ имеет положение одноосной гравитационной ориентации, в котором ось Cz коллинеарна оси С (т.е. (т.е.  = = =0), а положения осей Cx и Cy не определены (угол =0), а положения осей Cx и Cy не определены (угол  может принимать любые значения). Покажем, что момент может принимать любые значения). Покажем, что момент 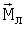 позволяет при наличии демпфирования обеспечить стабилизацию ИСЗ в положении равновесия, соответствующем любому наперед заданному значению угла позволяет при наличии демпфирования обеспечить стабилизацию ИСЗ в положении равновесия, соответствующем любому наперед заданному значению угла  и нулевым значениям углов и нулевым значениям углов  и и  . Для этого подставим в (8) значения . Для этого подставим в (8) значения  = = =0, =0,  = = 0=const. Закон полупассивного управления ИСЗ в данном случае примет вид 0=const. Закон полупассивного управления ИСЗ в данном случае примет вид

Докажем, что полупассивное управление (11) при наличии демпфирования в системе ИСЗ решает задачу трехосной стабилизации ИСЗ в орбитальной системе координат. Вначале рассмотрим случай малых значений наклонения i и докажем существование и асимптотическую устойчивость положения равновесия  = = =0, =0,  = = 0=const, a затем рассмотрим случай произвольных значений наклонения i и докажем устойчивость данного положения равновесия при постоянно действующих возмущениях. 0=const, a затем рассмотрим случай произвольных значений наклонения i и докажем устойчивость данного положения равновесия при постоянно действующих возмущениях.
При рассмотрении малых колебаний ИСЗ справедливо предположение о малости углов  , ,  и и  1= 1= – – 0 и их производных по времени. Поэтому в окрестности рассматриваемого положения равновесия моменты 0 и их производных по времени. Поэтому в окрестности рассматриваемого положения равновесия моменты   и и 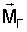 могут быть разложены в ряды по степеням этих малых величин. В результате получим их проекции с точностью до членов второго порядка малости в виде могут быть разложены в ряды по степеням этих малых величин. В результате получим их проекции с точностью до членов второго порядка малости в виде
МЛх=l11(t) +l12(t) +l12(t) +l13(t) +l13(t) 1, 1,
МЛy=l12(t) +l22(t) +l22(t) +l23(t) +l23(t) 1, 1,
МЛz=l13(t) +l23(t) +l23(t) +l33(t) +l33(t) 1, 1,
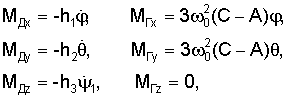
где
l11(t)=-k[( C C BC BC – – C C BC BC )2+( )2+( C C cos cos 0+ 0+ С С sin sin 0)2B2 C 0)2B2 C ], ],
l12(t)=l21(t)=-k( C C cos cos 0+ 0+ C C sin sin 0)×( 0)×( C C cos cos 0– 0– C C sin sin 0)B2 C 0)B2 C , ,
l13(t)=l31(t)=k( C C BC BC – – C C BC BC )( )( C C cos cos 0– 0– C C sin sin 0)BC 0)BC , ,
l22(t)=-k[( C C BC BC – – C C BC BC )2+( )2+( C C cos cos 0– 0– C C sin sin 0)B2 C 0)B2 C ], ],
l23(t)=l32(t)=-k( C C BC BC – – C C BC BC )( )( C C cos cos 0+ 0+ C C sin sin 0)BC 0)BC , ,
l33(t)=-k( 2 C 2 C + + 2 C 2 C )BC )BC . .
Уравнения (9) в матричной форме примут вид
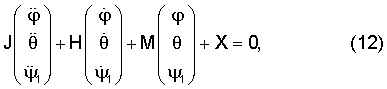
где
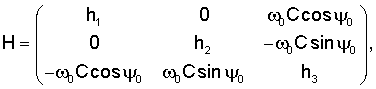

X – вектор с компонентами Xj (t,  , ,  , ,  1) 1)  нелинейным образом зависящими от нелинейным образом зависящими от  , ,  , ,  1. 1.
Компоненты mij(t) матрицы М, зависящие, вообще говоря, от малого параметра sin i, представим в виде суммы членов 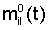 (t), не зависящих от i и членов (t), не зависящих от i и членов 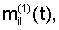 содержащих множителем sin i. Тогда содержащих множителем sin i. Тогда
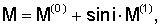
где М(0) получается из М заменой lij(t) на 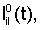 а а 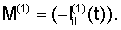
Рассмотрим систему линейного приближения уравнений (12) при i=0:
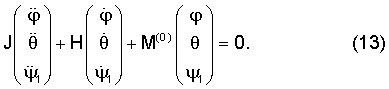
Поскольку при i=0 имеют место равенства  C C =R( =R( 0– 0– З), З),  С С = = С С =0, а также на основании (6) =0, а также на основании (6)

где 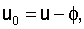 то то 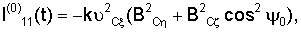 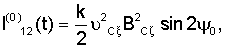  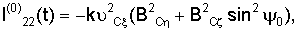 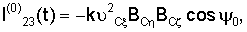 
причем BC , BC , BC , BC , BC определяются по формулам (14). определяются по формулам (14).
Представим 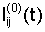 в виде в виде 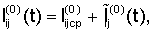 где где  – среднее по t значение функции – среднее по t значение функции 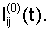 Тогда Тогда
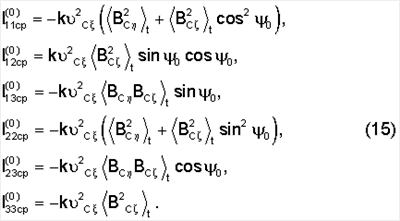
Вычислим необходимые средние по времени:

В результате матрица М будет представлена в виде
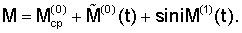
Подставив приведенные выше числовые значения гауссовых коэффициентов, нетрудно убедиться, что при выполнении неравенства k>0 матрица  является положительно определенной для любых значений является положительно определенной для любых значений  0. Если, кроме того, потребовать, чтобы выполнялось условие А>С, то матрица 0. Если, кроме того, потребовать, чтобы выполнялось условие А>С, то матрица
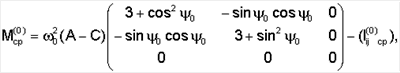
также будет являться положительно определенной. Если же разность А-С может принимать значения произвольного знака, то при выполнении неравенств

матрица 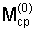 снова является положительно определенной и, следовательно, нулевое решение системы снова является положительно определенной и, следовательно, нулевое решение системы

асимптотически устойчиво.
Далее рассмотрим матрицу 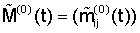 и оценим ее норму. и оценим ее норму.
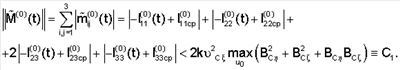
Поскольку постоянная С1 зависит лишь от матрицы  то и нулевое решение дифференциальной системы то и нулевое решение дифференциальной системы

также асимптотически устойчиво /11/. Причем эта асимптотическая устойчивость является равномерной, поскольку коэффициенты системы (18) почти периодичны по t. Кроме того, из экспоненциальной асимптотической устойчивости нулевого решения системы (18) вытекает экспоненциально-асимптотическая устойчивость нулевого решения исходной нелинейной системы (12) при i=0 /12/. Это и доказывает возможность полупассивной стабилизации ИСЗ при i=0.
В случае орбит малого наклонения (i 0, но sin i – мало), дифференциальные уравнения возмущенного движения (12) удобно записать в виде 0, но sin i – мало), дифференциальные уравнения возмущенного движения (12) удобно записать в виде

Согласно теореме об устойчивости при постоянно действующих возмущениях /12/, равномерная асимптотическая устойчивость нулевого решения системы (18) является достаточным условием устойчивости этого решения при постоянно действующих возмущениях. В качестве последних можно рассматривать малые по норме возмущения
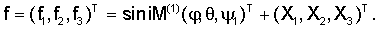
Более того, из экспоненциальной асимптотической устойчивости нулевого решения системы (18) в силу неравенств
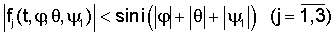
следует асимптотическая устойчивость нулевого решения исходной нелинейной системы (12) при достаточно малых значениях i /12/.
Таким образом, при наличии полупассивного управления (11) и демпфирования и выполнении неравенств (17) в условиях гравитационных возмущений достигается устойчивость стабилизируемого решения  = = =0, =0,  = = 0 при постоянно действующих возмущениях и асимптотическая устойчивость при достаточно малых значениях i, что служит обоснованием применения заявляемого способа для орбит малого наклонения. 0 при постоянно действующих возмущениях и асимптотическая устойчивость при достаточно малых значениях i, что служит обоснованием применения заявляемого способа для орбит малого наклонения.
Перейдем к рассмотрению задачи о стабилизации ИСЗ, находящихся на орбитах среднего и большого наклонений. Представим матрицу М в виде  Здесь матрица Мcp – результат покомпонентного усреднения матрицы М по времени, т.е. Здесь матрица Мcp – результат покомпонентного усреднения матрицы М по времени, т.е.

где 
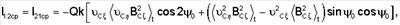
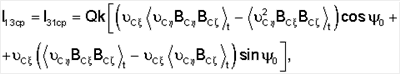

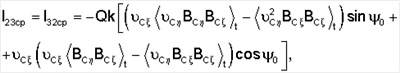

Вычислим необходимые средние:


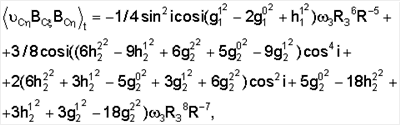



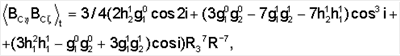
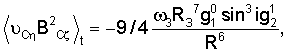
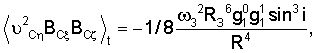
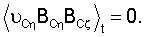
Рассмотрим сначала систему линейного приближения уравнений (12):
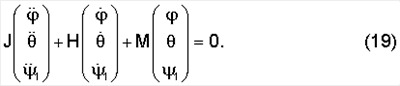
Если заменить в ней матрицу М ее средним значением, получим:

С помощью замены  = = 0t, x1= 0t, x1= ‘, x2= ‘, x2= ‘, x3= ‘, x3= ‘1, x4= ‘1, x4= , x5= , x5= , x6= , x6= 1, систему (19) можно привести к нормальному безразмерному виду 1, систему (19) можно привести к нормальному безразмерному виду

а систему (20) – к виду x’=Nx, где x=(x1, … x6)T, штрих означает производную по безразмерной переменной  , С0=cos , С0=cos 0, S0=sin 0, S0=sin 0, 0,

Система x’=Nx имеет ограниченные решения на полуоси [0, + ] тогда и только тогда, когда действительные части корней характеристического уравнения det( ] тогда и только тогда, когда действительные части корней характеристического уравнения det( I-N)=0 неположительны. Проведенный с помощью ЭВМ численный анализ показал, что существует область параметров ИСЗ и его орбиты, при которых выполнено это условие и, следовательно, в этой области действительные части собственных значений матрицы N удовлетворяют неравенствам Re I-N)=0 неположительны. Проведенный с помощью ЭВМ численный анализ показал, что существует область параметров ИСЗ и его орбиты, при которых выполнено это условие и, следовательно, в этой области действительные части собственных значений матрицы N удовлетворяют неравенствам Re j<- j<- , j=1…6, , j=1…6,  =const>0. =const>0.
Согласно /13/ введем в рассмотрение функцию
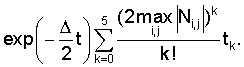
Обозначим через D наибольшее значение этой функции на полуоси [0, + ]. Если ]. Если 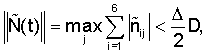 то нулевое решение системы (21) (или (19)) асимптотически устойчиво /13/. Следовательно, нулевое решение исходной нелинейной системы (12) будет устойчивым при постоянно действующих возмущениях /12/. то нулевое решение системы (21) (или (19)) асимптотически устойчиво /13/. Следовательно, нулевое решение исходной нелинейной системы (12) будет устойчивым при постоянно действующих возмущениях /12/.
Большое количество проведенных численных экспериментов показывает, что если параметры системы удовлетворяют неравенствам

то есть матрица Мср положительно определенная, то все перечисленные выше условия удовлетворяются и, следовательно, стабилизируемое движение  = = =0, =0,  = = 0=const устойчиво при постоянно действующих возмущениях. 0=const устойчиво при постоянно действующих возмущениях.
Таким образом доказана возможность использования лоренцевых сил для трехосной стабилизации динамически симметричного ИСЗ в орбитальной системе координат.
Способ может быть осуществлен с помощью известных технических средств, позволяющих создать двойной электростатический слой на поверхности ИСЗ. Величина и направление вектора дипольного момента двойного слоя определяются вышеприведенными условиями (11).
С целью подтверждения эффективности предложенного метода полупассивного управления ориентацией ИСЗ проведена серия численных экспериментов с помощью ЭВМ.
Для каждого набора значений параметров ИСЗ, его орбиты и начальных условий движения, расчеты выполнялись по двум математическим моделям – соответственно при наличии полупассивного управления по закону (11) и при его отсутствии. В результате построены графики зависимостей “самолетных” углов ориентации ИСЗ от аргумента широты – безразмерной угловой величины u= 0t на интервале 0 0t на интервале 0 u u 60, что соответствует примерно 10 оборотам ИСЗ по орбите. 60, что соответствует примерно 10 оборотам ИСЗ по орбите.
На Фиг.4 приведены результаты расчетов стабилизируемого движения ИСЗ  = = = 0, = 0,  = = 0 = 1 при следующих значениях параметров ИСЗ и его орбиты: R=7·106 м, i=1.045 рад, А=103 кг·м2, С/А=0.75, h1=h2=h3=h=0.5. В качестве начальных значений выбраны 0 = 1 при следующих значениях параметров ИСЗ и его орбиты: R=7·106 м, i=1.045 рад, А=103 кг·м2, С/А=0.75, h1=h2=h3=h=0.5. В качестве начальных значений выбраны  (0)=0.2 рад, (0)=0.2 рад,  (0)=0.2 рад, (0)=0.2 рад,  (0)=0.2 рад, (0)=0.2 рад,  x(0)=0.1 рад/с, x(0)=0.1 рад/с,  y(0)=1.1 рад/с, y(0)=1.1 рад/с,  z(0)=0.1 рад/с. z(0)=0.1 рад/с.
На Фиг.5 представлены колебания ИСЗ при отсутствии управления при тех же значениях параметров и начальных условий. В этом случае для компонент вектора  были взяты следующие значения: Рx=Рy=0, Рz=5·10-3 Кл·м. были взяты следующие значения: Рx=Рy=0, Рz=5·10-3 Кл·м.
На Фиг.4 и 5 сплошной линией показаны зависимости  = = (u), пунктирной – (u), пунктирной –  = = (u), штрихпунктирной – (u), штрихпунктирной –  = = (u). (u).
Сравнение графиков на Фиг.4 и 5 показывает, что введение в систему ИСЗ предложенного полупассивного управления позволяет за короткое время достичь режима стабилизированного движения. При этом полностью отсутствует необходимость в установке гироскопов, маховиков и т.п., обеспечивающих стабилизацию положения ИСЗ, а также в расходовании какого-либо рабочего вещества исполнительным механизмом. Очевидная простота закона управления, не требующего измерять какие-либо углы ориентации, их производные по времени и пр. в процессе движения ИСЗ, а также надежность и экономичность способа свидетельствуют в пользу перспективности его использования для стабилизации ИСЗ.
Работа выполнена при финансовой поддержке РФФИ (грант №05-01-01073).
Источники информации
1. А.П.Коваленко. Магнитные системы управления космическими летательными аппаратами. М.: Машиностроение, 1975, 248 с.
2. Сарычев В.А., Овчинников М.Ю. Магнитные системы ориентации искусственных спутников Земли. “Исследование космического пространства, т.23 (Итоги науки и техники ВИНИТИ АН СССР)” М., 1985, 104 с.
3. Франция, заявка №2550757, МКИ B64G 1/36 “Способ регулирования положения спутников”.
4. ФРГ, заявка № os 3329955, МКИ B64G 1/24, G05D 1/08 “Устройство для регулирования положения искусственных спутников”.
5. Япония, заявка №5940679, МКИ B64G 1/24 “Устройство, создающее вращательный момент для управления искусственным спутником и другими космическими аппаратами”.
6. Петров К.Г., Тихонов А.А. Патент RU – №2191146 – С1 на изобретение “Способ полупассивной стабилизации искусственного спутника Земли и устройство для его реализации”, МПК 7 В64С 1/32, 1/38 по заявке №2001107811, Приоритет 16.03.01, 34 с.
7. Труханов К.А., Рябова Т.Я., Морозов Д.Х. Активная защита космических кораблей. М.: Атомиздат, 1970, 229 с.
11. Беллман Р. Теория устойчивости решений дифференциальных уравнений. Изд-во иностр. лит-ры, M., 1954, 216 с.
12. Малкин И.Г. Теория устойчивости движения. M.: Наука, 1966, 530 с.
13. Мартынюк А.А. и др. Устойчивость движения: метод интегральных неравенств. Киев, Наук. думка, 1989, 272 с.
Формула изобретения
Способ полупассивной трехосной стабилизации динамически симметричного искусственного спутника Земли, включающий получение управляющего крутящего момента лоренцевых сил путем распределения на части поверхности спутника двойного электростатического слоя с заданным суммарным дипольным моментом 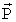 и согласованного изменения величины и направления этого момента, отличающийся тем, что указанный дипольный момент изменяют согласно условиям: и согласованного изменения величины и направления этого момента, отличающийся тем, что указанный дипольный момент изменяют согласно условиям:
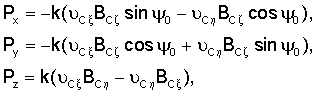
где Pх, Рy, Pz – проекции вектора 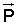 на главные центральные оси инерции Сх, Су, Сz спутника; на главные центральные оси инерции Сх, Су, Сz спутника;
  – проекции вектора – проекции вектора  скорости центра масс (C) спутника относительно геомагнитного поля на оси С скорости центра масс (C) спутника относительно геомагнитного поля на оси С , С , С орбитальной системы координат, причем ось С орбитальной системы координат, причем ось С направлена по касательной к орбите спутника в сторону его движения; направлена по касательной к орбите спутника в сторону его движения;
BC , BC , BC , ВC , ВC – проекции вектора – проекции вектора  индукции геомагнитного поля в центре масс спутника на оси C индукции геомагнитного поля в центре масс спутника на оси C , С , С , С , С , орбитальной системы координат; , орбитальной системы координат;
 0 – угол поворота спутника вокруг оси Cz его динамической симметрии, совпадающей с местной вертикалью (-С 0 – угол поворота спутника вокруг оси Cz его динамической симметрии, совпадающей с местной вертикалью (-С ) в режиме ориентированного движения; ) в режиме ориентированного движения;
k – постоянный коэффициент.
РИСУНКИ
|