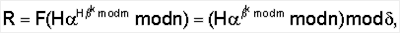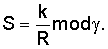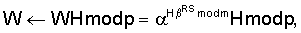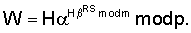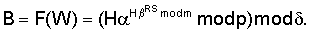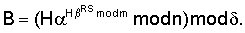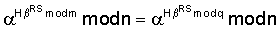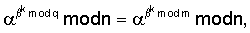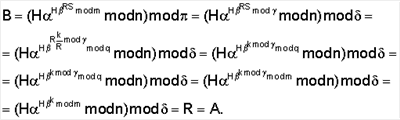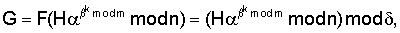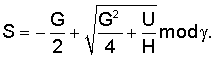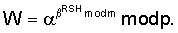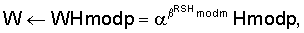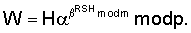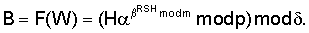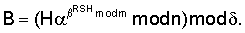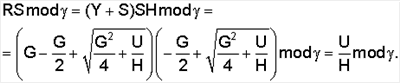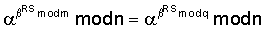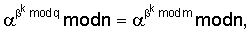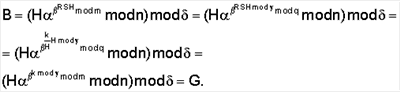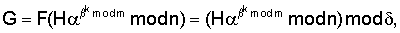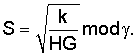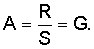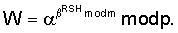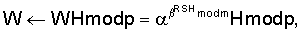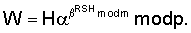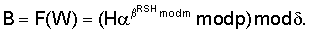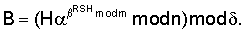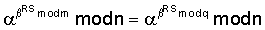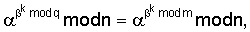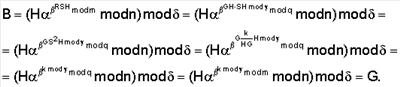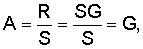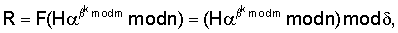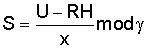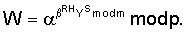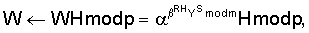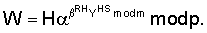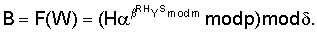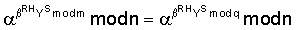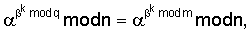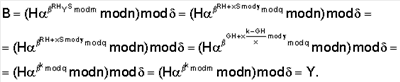Патент на изобретение №2325768
|
||||||||||||||||||||||||||
(54) СПОСОБ ГЕНЕРАЦИИ И ПРОВЕРКИ ПОДЛИННОСТИ ЭЛЕКТРОННОЙ ЦИФРОВОЙ ПОДПИСИ, ЗАВЕРЯЮЩЕЙ ЭЛЕКТРОННЫЙ ДОКУМЕНТ
(57) Реферат:
Изобретение относится к области электросвязи, а именно к области криптографических устройств и способов проверки электронной цифровой подписи (ЭЦП). Техническим результатом является уменьшение размера ЭЦП без снижения ее уровня стойкости. В способе формируют секретный ключ (СК), включающий три простых многоразрядных двоичных числа р, q и
Изобретение относится к области электросвязи и вычислительной техники, а конкретнее к области криптографических способов аутентификации электронных сообщений, передаваемых по телекоммуникационным сетям и сетям ЭВМ, и может быть использовано в системах передачи электронных сообщений (документов), заверенных электронной цифровой подписью (ЭЦП) (толкование используемых в описании терминов приведено в Приложении 1). Известен способ формирования и проверки ЭЦП, описанный в книгах [1. М.А. Иванов. Криптография. М., КУДИЦ-ОБРАЗ, 2001; 2. А.Г. Ростовцев, Е.Б. Маховенко. Введение в криптографию с открытым ключом. С-Петербург, Мир и семья, 2001. – с.43]. Известный способ заключается в следующей последовательности действий: формируют секретный ключ в виде трех простых МДЧ p, q и d, формируют открытый ключ (n, е) в виде пары МДЧ n и e, где n – число, представляющее собой произведение двух простых МДЧ p и q, и е – МДЧ, удовлетворяющее условию ed=1 mod (p-1)(q-1), принимают электронный документ, представленный МДЧ Н, в зависимости от значения Н и значения секретного ключа формируют ЭЦП в виде МДЧ Q=S=Hd mod n; формируют первое проверочное МДЧ А=Н; формируют второе проверочное МДЧ В, для чего МДЧ S возводят в целочисленную степень е по модулю n:В=Se mod n; сравнивают сформированные проверочные МДЧ А и В; при совпадении параметров сравниваемых МДЧ А и В делают вывод о подлинности ЭЦП. Недостатком известного способа является относительно большой размер подписи и необходимость увеличения размера подписи при разработке новых более эффективных алгоритмов разложения числа n на множители или при росте производительности современных вычислительных устройств. Это объясняется тем, что значение элемента подписи S вычисляется путем выполнения арифметических операций по модулю n, а стойкость ЭЦП определяется сложностью разложения модуля n на множители p и q. Известен также способ проверки ЭЦП Эль-Гамаля, описанный в книге [Молдовян А.А., Молдовян Н.А., Советов Б.Я. Криптография. – СПб, Лань, 2000. – С.156-159], который включает следующие действия: формируют простое МДЧ p и двоичное число G, являющееся первообразным корнем по модулю p, генерируют секретный ключ в виде МДЧ x, в зависимости от x формируют открытый ключ в виде МДЧ Y=Gx mod p, принимают электронный документ (ЭД), представленный в виде МДЧ Н, в зависимости от Н и секретного ключа формируют ЭЦП Q в виде двух МДЧ S и R, то есть Q=(R, S); осуществляют процедуру проверки ЭЦП, включающую вычисление двух контрольных параметров с использованием исходных МДЧ p, G, Y, Н, R и S путем возведения МДЧ G, Y, R в дискретную степень по модулю p и сравнение вычисленных контрольных параметров; при совпадении значений контрольных параметров делают вывод о подлинности ЭЦП. Недостатком данного способа также является относительно большой размер ЭЦП. Это объясняется тем, что значения элементов подписи S и R вычисляются путем выполнения арифметических операций по модулю p – 1 и по модулю p соответственно. формируют секретный ключ в виде трех простых МДЧ p, q и формируют первое проверочное МДЧ А, для чего МДЧ S возводят в степень Н по модулю n; формируют второе проверочное МДЧ В, для чего МДЧ сравнивают сформированные проверочные МДЧ А и В; при совпадении параметров сравниваемых МДЧ А и В делают вывод о подлинности ЭЦП. Недостатком ближайшего аналога также является относительно большой размер подписи, что обусловлено необходимостью вычисления значения S путем выполнения арифметических операций по модулю n, размер которого для обеспечения требуемого уровня стойкости ЭЦП составляет 1024 бит и более. Целью изобретения является разработка способа генерации и проверки подлинности ЭЦП, заверяющей ЭД, обеспечивающего уменьшение размера подписи без снижения уровня стойкости ЭЦП. Поставленная цель достигается тем, что в известном способе генерации и проверки подлинности ЭЦП, заверяющей ЭД, заключающемся в том, что формируют секретный ключ, включающий три простых МДЧ p, q и Новым также является то, что первое проверочное МДЧ А формируют путем вычитания значения S из значения R. Новым также является то, что первое проверочное МДЧ А формируют путем выполнения операции деления значения R на значение S. Новым также является то, что промежуточное МДЧ W формируют путем возведения числа Новым также является то, что промежуточное МДЧ W формируют путем возведения числа Новым также является то, что промежуточное МДЧ W формируют путем возведения числа Новым является также и то, что сжимающее преобразование промежуточного МДЧ W выполняют с помощью хэш-функции. Новым является также и то, что сжимающее преобразование промежуточного МДЧ W выполняют с помощью операции взятия остатка от деления промежуточного МДЧ W на простое число 6, длина которого лежит в пределах от 64 до 256 бит. Благодаря новой совокупности существенных признаков путем изменения процедуры формирования проверочных МДЧ достигается уменьшение размера подписи, а выбором фиксированного размера секретного МДЧ Проведенный анализ уровня техники позволил установить, что аналоги, характеризующиеся совокупностью признаков, тождественных всем признакам заявленного технического решения, отсутствуют в известных источниках информации, что указывает на соответствие заявленного изобретения условию патентоспособности «новизна». Результаты поиска известных решений в данной и смежных областях с целью выявления признаков, совпадающих с отличительными от ближайшего аналога признаками заявленного объекта, показали, что они не следуют явным образом из уровня техники, что указывает на соответствие заявленного изобретения условию «изобретательский уровень». Возможность реализации заявленного способа объясняется следующим образом. Известно, что сложность задачи разложения целого числа на два больших простых множителя зависит от длины последних, поэтому при появлении новых методов разложения увеличивают длину его простых множителей. Открытый ключ формируют в виде простого числа n=Npq+1 в зависимости от секретных простых чисел p и q, выбираемых такими, чтобы число q-1 делились на простое число
и
где F(W) есть некоторая сжимающая функция, вычисляемая путем выполнения сжимающего преобразования числа, являющегося ее аргументом, а элемент подписи R вычисляется по предварительно выбираемому случайному числу k по формуле С учетом выбора чисел
Владелец секретного числа Рассмотрим примеры реализации заявленного технического решения с искусственно уменьшенной разрядностью используемых чисел. Пример 1. Реализации заявляемого способа с иллюстрацией конкретных численных значений. Приводимые в примере МДЧ записаны для краткости в виде десятичных чисел, которые в вычислительных устройствах представляются и преобразуются в двоичном виде, т.е. в виде последовательности сигналов высокого и низкого потенциала. При проверке подлинности ЭЦП выполняют следующую последовательность действий. 1. Формируют секретный ключ в виде тройки МДЧ (p, q, 2. Формируют открытый ключ в виде тройки чисел (n, МДЧ n=2pq+1=1144984542083, где m=pq=572492271041; МДЧ МДЧ 3. Принимают открытый ключ подписывающего (n, 4. Принимают ЭД, представленный, например, следующим МДЧ Н (в качестве которого может быть взята, в частности, хэш-функция от ЭД): H=37975637. 5. Формируют ЭЦП Q в виде пары чисел (R, S), для чего выполняют следующие действия: 5.1. Задают случайное число k=4757231. 5.2. Формируют элемент подписи R путем выполнения операций, задаваемых формулой где 5.3. Формируют элемент подписи S путем выполнения операций, задаваемых формулой
S=31318832. 6. Формируют первое проверочное МДЧ А в зависимости от ЭЦП Q=(R, S): A=R=73802. 7. Генерируют промежуточное МДЧ W в соответствии с формулой W= W=2916219444376609 mod1144984542083=940022876369. 8. Формируют второе проверочное МДЧ В путем сжимающего преобразования промежуточного МДЧ W: В=F(W)=(W)mod 9. Сравнивают (например, поразрядно) параметры первого и второго проверочных чисел А и В. Сравнение показывает, что параметры МДЧ А и В совпадают, что указывает на подлинность ЭЦП, т.е. принятая ЭЦП относится к принятому ЭД, представленному МДЧ Н, и сформирована подписывающим, которому соответствует принятый открытый ключ (n, Рассмотренные в примере реализации заявленного способа действия обеспечивают корректность работы заявляемого способа в общем случае, т.е. для произвольной длины чисел n, Правильное значение ЭЦП можно вычислить только при знании секретного МДЧ В приводимых ниже дополнительных примерах реализации заявляемого способа не указывается конкретное значение численных значений. Корректность работы способа доказывается математическим способом для произвольных значений параметров, выбранных в соответствии с описанием изобретения и конкретизацией вариантов реализации в отдельных примерах. Пример 2. Реализация заявляемого способа для выработки ЭЦП длиной 240 бит. В данном примере используется число 1. Формируют секретный ключ в виде тройки чисел (p, q, 2. Формируют открытый ключ в виде тройки чисел (n, 3. Принимают открытый ключ подписывающего (n, 4. Принимают ЭД, представленный, например, следующим МДЧ Н (в качестве которого может быть взята, в частности, хэш-функция от ЭД). 5. Формируют ЭЦП Q в виде пары чисел (R, S), для чего выполняют следующие действия: 5.1. Задают случайное число k. 5.2. Формируют элемент подписи R путем выполнения операций, задаваемых формулой где 5.3. Формируют элемент подписи S путем выполнения операций, задаваемых формулой
Поскольку эта формула задает вычисление по модулю длины 160 бит, то значение S имеет длину 160 бит. С учетом длины элемента подписи R получаем длину ЭЦП – 240 бит. 6. Формируют первое проверочное МДЧ А в зависимости от ЭЦП Q=(R, S): A=R=73802. 7. Генерируют промежуточное МДЧ W в соответствии с формулой W=
8. Преобразуют промежуточное МДЧ W в соответствии с формулой
в результате чего получаем значение:
9. Формируют второе проверочное МДЧ В путем сжимающего преобразования промежуточного МДЧ W:
10. Сравнивают (например, поразрядно) параметры первого и второго проверочных чисел А и В. Совпадение значений А и В будет означать, что ЭЦП является подлинной, т.е. относящейся к принятому ЭД, представленному МДЧ Н, и сформирована подписывающим, которому соответствует принятый открытый ключ (n, Это доказывается теоретически следующим образом. Мы имеем
Поскольку
и
поэтому справедливы следующие преобразования: Пример 3. Реализация заявляемого способа для выработки ЭЦП длиной 320 бит. В данном примере используется число 1. Формируют секретный ключ в виде тройки чисел (p, q, 2. Формируют открытый ключ в виде тройки чисел (n, 3. Принимают открытый ключ подписывающего (n, 4. Принимают ЭД, представленный, например, следующим МДЧ Н (в качестве которого может быть взята, в частности, хэш-функция от ЭД). 5. Формируют ЭЦП Q в виде пары чисел (R, S), для чего выполняют следующие действия: 5.1. Задают случайное число k. 5.2. Генерируют вспомогательное МДЧ G в соответствии с формулой:
где 5.3. Формируют элемент подписи S путем выполнения операций, задаваемых формулой
Поскольку эта формула задает вычисление по модулю длины 160 бит, то значение S имеет длину 160 бит. 5.4. Формируют элемент подписи R в соответствии с формулой R=S+G. Поскольку значения S и G имеют длину 160 бит, то значение R также имеет длину примерно 160 бит. С учетом длины элементов подписи R и S получаем длину ЭЦП – 320 бит. 6. Формируют первое проверочное МДЧ А: А=R-S. 7. Генерируют промежуточное МДЧ W в соответствии с формулой W=
8. Преобразуют промежуточное МДЧ W в соответствии с формулой
в результате чего получаем значение:
9. Формируют второе проверочное МДЧ В путем сжимающего преобразования промежуточного МДЧ W:
10. Сравнивают (например, поразрядно) параметры первого и второго проверочных чисел А и В. Совпадение значений А и В будет означать, что ЭЦП является подлинной, т.е. относящейся к принятому ЭД, представленному МДЧ H, и сформирована подписывающим, которому соответствует принятый открытый ключ (n, Это доказывается теоретически следующим образом. Мы имеем
Вычислим значение Поскольку
и
поэтому справедливы следующие преобразования: Поскольку A=R-S=(G-S)+S, то A=B. Пример 4. Реализация заявляемого способа для выработки ЭЦП длиной 400 бит. В данном примере используется число 1. Формируют секретный ключ в виде тройки чисел (p, q, 2. Формируют открытый ключ в виде тройки чисел (n, 3. Принимают открытый ключ подписывающего (n, 4. Принимают ЭД, представленный, например, следующим МДЧ Н (в качестве которого может быть взята, в частности, хэш-функция от ЭД). 5. Формируют ЭЦП Q в виде пары чисел (R, S), для чего выполняют следующие действия: 5.1. Задают случайное число k. 5.2. Генерируют вспомогательное МДЧ G в соответствии с формулой:
где 5.3. Формируют элемент подписи S путем выполнения операций, задаваемых формулой
Поскольку эта формула задает вычисление по модулю длины 160 бит, то значение S имеет длину 160 бит. 5.4. Формируют элемент подписи R в соответствии с формулой R=S·G. Поскольку значения S имеет длину 160 бит и G имеет длину 80 бит, то значение R, получаемое как произведение значений S и G, имеет длину, равную сумме длин значений S и G, то есть имеет длину 240 бит. С учетом длины элементов подписи R и S получаем длину ЭЦП – 400 бит. 6. Формируют первое проверочное МДЧ А:
7. Генерируют промежуточное МДЧ W в соответствии с формулой W=
8. Преобразуют промежуточное МДЧ W в соответствии с формулой
в результате чего получаем значение:
9. Формируют второе проверочное МДЧ В путем сжимающего преобразования промежуточного МДЧ W:
10. Сравнивают (например, поразрядно) параметры первого и второго проверочных чисел А и В. При формировании подписи по секретному ключу значения А и В будут совпадать, что означает подлинность ЭЦП, т.е. то, что ЭЦП относится к принятому ЭД, представленному МДЧ Н, и сформирована подписывающим, которому соответствует принятый открытый ключ (n,
Поскольку
и
поэтому справедливы следующие преобразования: Поскольку
то A=B. Пример 5. Реализация заявляемого способа для выработки ЭЦП длиной 240 бит. В данном примере используется число 1. Формируют секретный ключ в виде тройки чисел (p, q, 2. Формируют открытый ключ в виде тройки чисел (n, 3. Генерируют первое вспомогательное случайное МДЧ x. 4. Генерируют второе вспомогательное МДЧ Y= 5. Принимают открытый ключ подписывающего (n, 6. Принимают ЭД, представленный, например, следующим МДЧ H (в качестве которого может быть взята, в частности, хэш-функция от ЭД). 7. Формируют ЭЦП Q в виде пары чисел (R, S), для чего выполняют следующие действия: 7.1. Задают случайное число k. 7.2. Формируют элемент подписи R в соответствии с формулой:
где 7.3. Формируют элемент подписи S в соответствии с формулой:
Поскольку эта формула задает вычисление по модулю длины 160 бит, то значение S имеет длину 160 бит. С учетом длины элементов подписи R и S получаем длину ЭЦП – 240 бит. 8. Формируют первое проверочное МДЧ А: А=R. 9. Генерируют промежуточное МДЧ W в соответствии с формулой W=
10. Преобразуют промежуточное МДЧ W в соответствии с формулой
в результате чего получаем значение:
11. Формируют второе проверочное МДЧ В путем сжимающего преобразования промежуточного МДЧ W:
12. Сравнивают (например, поразрядно) параметры первого и второго проверочных чисел А и В. Совпадение значений А и В означает, что ЭЦП является подлинной, т.е. относящейся к принятому ЭД, представленному МДЧ Н, и сформирована подписывающим, которому соответствует принятый открытый ключ. Это доказывается теоретически следующим образом. В соответствии с процедурой проверки подлинности ЭЦП мы имеем
Поскольку
и
поэтому справедливы следующие преобразования: Поскольку A=G, то A=B. Таким образом, показано, что заявляемый способ может быть положен в основу стойких систем ЭЦП, обеспечивающих уменьшение размера подписи по сравнению с известными решениями и сохранение размера подписи при появлении новых более эффективных алгоритмов решения задачи разложения чисел на множители и задачи дискретного логарифмирования, т.е. низкую вероятность несанкционированного формирования ЭЦП («ложного» подтверждения подлинности ЭЦП). Приведенный пример и математическое обоснование показывают, что предлагаемый способ генерации и проверки подлинности электронной цифровой подписи работает корректно, технически реализуем и позволяет решить поставленную задачу. Приложение 1 Толкование терминов, используемых в описании 1. Двоичный цифровой электромагнитный сигнал – последовательность битов в виде нулей и единиц. 2. Параметры двоичного цифрового электромагнитного сигнала: разрядность и порядок следования единичных и нулевых битов. 3. Разрядность двоичного цифрового электромагнитного сигнала – общее число его единичных и нулевых битов, например, число 10011 является 5-разрядным. 4. Электронная цифровая подпись (ЭЦП) – двоичный цифровой электромагнитный сигнал, параметры которого зависят от подписанного электронного документа и от секретного ключа. Проверка подлинности ЭЦП осуществляют с помощью открытого ключа, который зависит от секретного ключа. 5. Электронный документ (ЭД) – двоичный цифровой электромагнитный сигнал, параметры которого зависят от исходного документа и способа его преобразования к электронному виду. 6. Секретный ключ – двоичный цифровой электромагнитный сигнал, используемый для формирования подписи к заданному электронному документу. Секретный ключ представляется, например, в двоичном виде как последовательность цифр «0» и «1». 7. Открытый ключ – двоичный цифровой электромагнитный сигнал, параметры которого зависят от секретного ключа и который предназначен для проверки подлинности цифровой электронной подписи. 8. Хэш-функция от электронного документа – двоичный цифровой электромагнитный сигнал, параметры которого зависят от электронного документа и выбранного метода ее вычисления. 9. Многоразрядное двоичное число – двоичный цифровой электромагнитный сигнал, интерпретируемый как двоичное число и представляемый в виде последовательности цифр «0» и «1». Z mod n, где W – число, являющееся результатом выполнения данной операции. 11. Функция Эйлера от натурального числа n – это число чисел, являющихся взаимно простыми с n и не превосходящими n [Виноградов И.М. Основы теории чисел. – М.: Наука, 1972. – 167 с.; Бухштаб А.А. Теория чисел. – М.: Просвещение, 1966. – 384 с]. 12. Показатель q по модулю n числа a, являющегося взаимно простым с n – это минимальное из чисел 13. Первообразный корень – это число, относящееся к показателю, который равен функции Эйлера от модуля. 14. Обратный элемент по модулю n к числу а, являющемуся взаимно простым с n, есть натуральное число, обозначаемое как а-1, для которого выполняется условие a-1a=1; для любого числа, являющегося взаимно простым с модулем, существует элемент, обратный этому числу. Известны эффективные алгоритмы вычисления обратных элементов [Романец Ю.В., Тимофеев П.А., Шаньгин В.Ф. Защита информации в компьютерных системах и сетях. – М.: Радио и связь. – С.308-310]. 15. Операция деления целого числа А на целое число В по модулю n выполняется как операция умножения по модулю n числа А на целое число В-1, которое является обратным к В по модулю n.
Формула изобретения
1. Способ генерации и проверки подлинности электронной цифровой подписи, заверяющей электронный документ, заключающийся в том, что формируют секретный ключ, включающий три простых многоразрядных двоичных числа р, q и 2. Способ по п.1, отличающийся тем, что первое проверочное многоразрядное двоичное число А формируют путем вычитания значения S из значения R. 3. Способ по п.1, отличающийся тем, что первое проверочное многоразрядное двоичное число А формируют путем выполнения операции деления значения R на значение S. 4. Способ по п.1, отличающийся тем, что промежуточное многоразрядное двоичное число W формируют путем возведения числа 5. Способ по п.1, отличающийся тем, что промежуточное многоразрядное двоичное число W формируют путем возведения числа 6. Способ по п.1, отличающийся тем, что промежуточное многоразрядное двоичное число W формируют путем возведения числа 7. Способ по п.1, отличающийся тем, что сжимающее преобразование промежуточного многоразрядного двоичного числа W выполняют с помощью хэш-функции. 8. Способ по п.1, отличающийся тем, что сжимающее преобразование промежуточного многоразрядного двоичного числа W выполняют с помощью операции взятия остатка от деления промежуточного многоразрядного двоичного числа W на простое число
|
||||||||||||||||||||||||||

 . Формируют открытый ключ (ОК), включающий три многоразрядных двоичных числа n,
. Формируют открытый ключ (ОК), включающий три многоразрядных двоичных числа n,  и
и  , где n=Epq+1, Е – четное число,
, где n=Epq+1, Е – четное число, 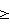 1 по модулю n: В=
1 по модулю n: В= WH mod n или W
WH mod n или W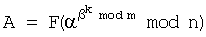
 ,
,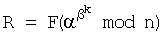 . Например, в качестве сжимающей функции можно использовать операцию взятия остатка от деления на МДЧ
. Например, в качестве сжимающей функции можно использовать операцию взятия остатка от деления на МДЧ  , имеющее заданную длину и определяющее размер значения функции F. В качестве сжимающей функции можно также использовать хэш-функции, описанные, например, в книге [Молдовян А.А., Молдовян Н.А. Введение в криптосистемы с открытым ключом. – СПб. БХВ-Петербург, 2005. – 286 с.; см. с.184-204].
, имеющее заданную длину и определяющее размер значения функции F. В качестве сжимающей функции можно также использовать хэш-функции, описанные, например, в книге [Молдовян А.А., Молдовян Н.А. Введение в криптосистемы с открытым ключом. – СПб. БХВ-Петербург, 2005. – 286 с.; см. с.184-204]. RSH mod
RSH mod 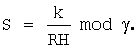

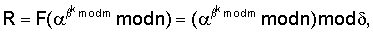

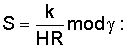
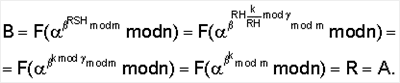
 выбирается равной 160 бит.
выбирается равной 160 бит.