Патент на изобретение №2159201
|
||||||||||||||||||||||||||
(54) СПОСОБ УПРАВЛЕНИЯ ОРИЕНТАЦИЕЙ ИСКУССТВЕННОГО СПУТНИКА ЗЕМЛИ
(57) Реферат: Изобретение относится к космической технике и может быть использовано для управления ориентацией искусственных спутников Земли (ИСЗ). Согласно изобретению, для получения управляющего крутящего момента, действующего на ИСЗ при его движении в геомагнитном поле, на части поверхности ИСЗ распределяют электрический заряд. Для достижения устойчивой ориентации ИСЗ согласованно изменяют величину заряда и координату центра заряда относительно центра масс ИСЗ. При этом выполняют условия, учитывающие гравитационные возмущения и обеспечивающие демпфирование колебаний ИСЗ. Изобретение направлено на повышение эффективности управления ориентацией ИСЗ. 3 ил. Изобретение относится к области космической техники и может быть использовано для управления ориентацией искусственных спутников Земли (ИСЗ) путем демпфирования колебаний. Известны способы управления ориентацией ИСЗ путем использования различных по своей природе сил – реактивных или внешних по отношению к ИСЗ сил, создающих управляющие моменты. Внешние по отношению к ИСЗ факторы, создающие управляющие моменты без расхода рабочего тела, используются в пассивных способах ориентации /1/. Использование пассивных способов управления ориентацией предпочтительно в тех случаях, когда во время активной фазы полета отклонение ИСЗ от заданного положения в пространстве не должно превышать нескольких градусов, а также когда не требуется выполнения сложных программных разворотов и противодействия большим возмущающим моментам /2/. Известны способы пассивной ориентации (стабилизации) ИСЗ, основанные на использовании природных геофизических факторов, например гравитационных сил, давления солнечного ветра, сил взаимодействия магнитного поля ИСЗ с внешним магнитным полем Земли, набегающего потока разреженного атмосферного воздуха. Однако известные способы характеризуются малой эффективностью либо вследствие того, что создание управляющего (стабилизирующего) момента требует значительных конструктивных усложнений, либо вследствие того, что область их практического применения достаточно сильно ограничена. Так, системы, использующие давление солнечного излучения, требуют больших рабочих поверхностей и могут быть эффективны лишь для ИСЗ, находящихся на высоких орбитах /1/. Эффективность аэродинамических систем, основанных на стабилизирующем воздействии набегающего на ИСЗ потока в разреженных слоях атмосферы, ограничена малыми орбитальными высотами и значительным влиянием атмосферы на параметры орбиты. Общим недостатком известных способов пассивной ориентации ИСЗ является сложность изменения управляющего момента, ограниченность использования в связи с невозможностью компенсации эксцентриситетных колебаний, возникающих на эллиптических орбитах. Известен способ управления ориентацией ИСЗ /3/, включающий получение управляющего – крутящего – момента вследствие воздействия природного геофизического фактора – солнечного света, оказывающего давление на часть поверхности ИСЗ, занятую солнечными батареями, при изменении площади поверхности батарей. Недостатки известного способа обусловлены зависимостью получения управляющего момента от наличия светового потока и его флуктуаций, обусловленных солнечной активностью. Способ требует больших трудозатрат и энергоресурсов и не позволяет осуществлять непрерывную стабилизацию движения, что снижает эффективность управления ориентацией ИСЗ. Известный способ выбран в качестве наиболее близкого аналога заявляемому изобретению. Задача изобретения состоит в повышении эффективности управления ориентацией ИСЗ. Задача решена тем, что в известном способе управления ориентацией ИСЗ, включающем получение управляющего крутящего момента при воздействии природного геофизического фактора на электрически заряженную часть поверхности ИСЗ и изменении характеристик такой поверхности, в соответствии с изобретением в качестве природного геофизического фактора используют магнитное поле Земли, на части поверхности ИСЗ распределяют электрический заряд (Q), а получение управляющего момента производят путем согласованного изменения величин электрического заряда и координаты центра заряда относительно центра масс ИСЗ, удовлетворяющего соотношениям 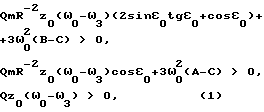 где z0 – координата центра заряда ИСЗ относительно центра масс ИСЗ вдоль оси, совпадающей в положении равновесия с направлением местной вертикали, m – магнитный момент земного диполя, R – радиус орбиты ИСЗ,  0 – орбитальная угловая скорость центра масс ИСЗ, 0 – орбитальная угловая скорость центра масс ИСЗ, з – угловая скорость суточного вращения Земли, з – угловая скорость суточного вращения Земли, 0 0 11.5 град. – угол между осями магнитного диполя и суточного вращения Земли, 11.5 град. – угол между осями магнитного диполя и суточного вращения Земли,A,B,C – главные центральные моменты инерции ИСЗ. Технический результат, достигаемый изобретением, состоит в том, что размещение заряда в локальной области поверхности (на экране) приводит к возбуждению сил Лоренца, воздействующих на часть поверхности ИСЗ, и демпфирующего момента, стабилизирующего колебания ИСЗ относительно орбитальной системы координат, а выполнение условий на согласованное изменение величины заряда Q и координаты центра заряда относительно центра масс ИСЗ z0 обеспечивает существование и устойчивость положения равновесия, т.е. решает задачу стабилизации ИСЗ в орбитальной системе координат (ОСК). Сущность изобретения поясняется фиг. 1, на которой представлена ОСК для описания вращательного движения ИСЗ относительно его центра масс; на фиг. 2, 3 представлены примеры результатов расчета положений равновесия ИСЗ в соответствии с изобретением и без него. Сущность изобретения заключается в следующем. Для ИСЗ, центр масс которого движется в гравитационном (ньютоновском центральном) поле Земли, а также совершает вращательное движение по скоростью  в магнитном поле Земли (МПЗ), которое аппроксимируется полем магнитного диполя с осью, образующей угол в магнитном поле Земли (МПЗ), которое аппроксимируется полем магнитного диполя с осью, образующей угол  0= 11,5 град. с осью суточного вращения Земли, и характеризуется магнитной индукцией 0= 11,5 град. с осью суточного вращения Земли, и характеризуется магнитной индукцией  распределение на части поверхности ИСЗ (далее – экран) электрического заряда распределение на части поверхности ИСЗ (далее – экран) электрического заряда 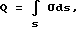 где где  – плотность распределения заряда, приводит к возникновению силы Лоренца – плотность распределения заряда, приводит к возникновению силы Лоренца 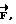 воздействующей на заряженный элемент экрана dS, равной воздействующей на заряженный элемент экрана dS, равной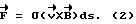 Можно показать, что главный момент 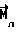 лоренцовых сил прямо пропорционален смещению центра заряда относительно центра масс ИСЗ и определяется выражением лоренцовых сил прямо пропорционален смещению центра заряда относительно центра масс ИСЗ и определяется выражением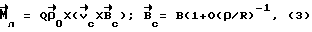 где 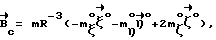  – радиус-вектор центра заряда ИСЗ относительно его центра масс, причем влияние характера распределения заряда по поверхности экрана на динамику ИСЗ пренебрежимо мало.
Для получения восстанавливающего момента, превышающего действующие возмущающие моменты, можно варьировать параметры заряженного экрана. Оценки показывают, что для орбиты радиуса R = 7 – радиус-вектор центра заряда ИСЗ относительно его центра масс, причем влияние характера распределения заряда по поверхности экрана на динамику ИСЗ пренебрежимо мало.
Для получения восстанавливающего момента, превышающего действующие возмущающие моменты, можно варьировать параметры заряженного экрана. Оценки показывают, что для орбиты радиуса R = 7  106 м, 106 м,  0= 1,1 0= 1,1 10-3 1/c, при использовании экрана площадью S = 150 кв.м., имеющего потенциал U = 3 10-3 1/c, при использовании экрана площадью S = 150 кв.м., имеющего потенциал U = 3  106 В и удельную емкость Cэ = 10-11Ф/кв.м, заряд Q = Cэ 106 В и удельную емкость Cэ = 10-11Ф/кв.м, заряд Q = Cэ  S S  U = 4,5 U = 4,5  10-3 Кл и, следовательно 10-3 Кл и, следовательно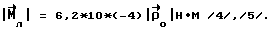 Путем увеличения смещения центра заряда можно увеличить 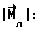 так, при так, при 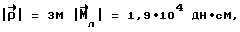 что превышает величину гравитационного момента для ИСЗ с характерными моментами инерции порядка 10 что превышает величину гравитационного момента для ИСЗ с характерными моментами инерции порядка 10  3 кг кв.м.
Поскольку потенциал U может быть увеличен на несколько порядков, момент лоренцовых сил может значительно превысить гравитационные и другие возмущающие моменты /6/.
Для определения условий, при которых достигается положение равновесия ИСЗ, нужно рассмотреть вращательное движение ИСЗ относительно его центра масс в орбитальной системе координат (ОСК) (фиг.1) с началом в центре масс ИСЗ, ось 3 кг кв.м.
Поскольку потенциал U может быть увеличен на несколько порядков, момент лоренцовых сил может значительно превысить гравитационные и другие возмущающие моменты /6/.
Для определения условий, при которых достигается положение равновесия ИСЗ, нужно рассмотреть вращательное движение ИСЗ относительно его центра масс в орбитальной системе координат (ОСК) (фиг.1) с началом в центре масс ИСЗ, ось 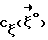 которой направлена по касательной к орбите в сторону движения, ось которой направлена по касательной к орбите в сторону движения, ось 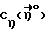 – по нормали к плоскости орбиты, ось – по нормали к плоскости орбиты, ось 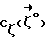 – вдоль радиуса-вектора – вдоль радиуса-вектора 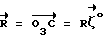 центра масс ИСЗ относительно центра Земли (здесь и далее используется правая декартова прямоугольная система координат), при этом вращение ОСК учитывается относительно инерциальной системы координат, в качестве которой принимается система центра масс ИСЗ относительно центра Земли (здесь и далее используется правая декартова прямоугольная система координат), при этом вращение ОСК учитывается относительно инерциальной системы координат, в качестве которой принимается система 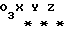 , ось , ось 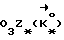 которой направлена по оси собственного вращения Земли, ось которой направлена по оси собственного вращения Земли, ось 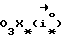 – в восходящий узел орбиты, а плоскость – в восходящий узел орбиты, а плоскость 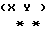 совпадает с плоскостью экватора. Кроме того, используется также жестко связанная с ИСЗ система его главных центральных осей инерции Cxyz (орты совпадает с плоскостью экватора. Кроме того, используется также жестко связанная с ИСЗ система его главных центральных осей инерции Cxyz (орты 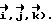 Ориентация ОСК относительно системы 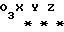 определяется равенствами: определяется равенствами: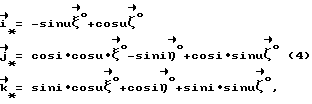 где 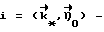 наклонение орбиты, наклонение орбиты,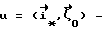 аргумент широты, u = аргумент широты, u =  0t 0t 0 – орбитальная угловая скорость центра масс ИСЗ.
Ориентация осей XYZ относительно осей 0 – орбитальная угловая скорость центра масс ИСЗ.
Ориентация осей XYZ относительно осей    определяется матрицей направляющих косинусов определяется матрицей направляющих косинусов  i, i, i, i, i (i = 1,2,3) так, что имеют место равенства i (i = 1,2,3) так, что имеют место равенства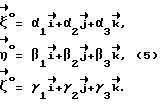 Вектор, характеризующий поле магнитного диполя, определяется по формуле /1/: 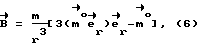 где 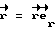 – радиус-вектор, направленный из точки Оз в данную точку пространства.
Выражая векторы, входящие в (6), через орты – радиус-вектор, направленный из точки Оз в данную точку пространства.
Выражая векторы, входящие в (6), через орты 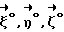 и вектор и вектор 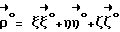 , предполагая, что в момент времени t = 0 точка C находилась в восходящем узле орбиты, а угол между ортом , предполагая, что в момент времени t = 0 точка C находилась в восходящем узле орбиты, а угол между ортом 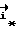 и составляющей орта и составляющей орта 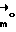 в плоскости в плоскости 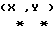 был равен был равен  0. Тогда орт 0. Тогда орт 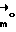 может быть представлен в виде может быть представлен в виде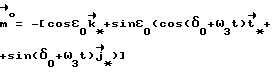 или, с учетом (4), в следующей эквивалентной форме: 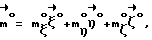 где  Орт 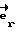 представим в виде представим в виде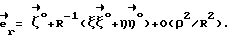 Поэтому 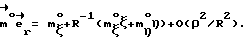 В результате, используя представление r-3= R-3[1-3  /R+O( /R+O( 2/R2)] 2/R2)]и учитывая, что 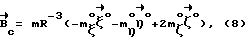 получим величину магнитной индукции МПЗ в центре масс ИСЗ. Ограничиваясь основным членом в разложении вектора 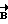 и выполнив интегрирование в формуле (2), получим и выполнив интегрирование в формуле (2), получим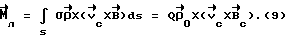 Здесь 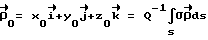 радиус-вектор центра заряда ИСЗ относительно его центра масс, и радиус-вектор центра заряда ИСЗ относительно его центра масс, и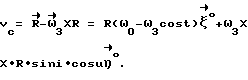 Используя формулы (8) и (9), можно выразить  через орты ОСК: через орты ОСК: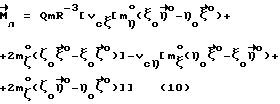 где vc  = R( = R( o– o– зcosi), vc зcosi), vc = R = R зsinicosu. зsinicosu.Отсюда с учетом формулы (5), найдем проекции  на оси Х, Y, Z: на оси Х, Y, Z: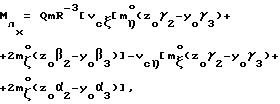 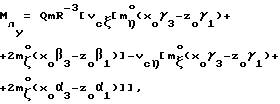 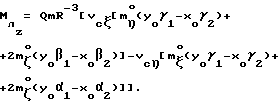 С учетом гравитационного момента вращательное движение ИСЗ под действием совместно  и и 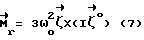 может быть описано следующей системой дифференциальных уравнений (схема Эйлера-Пуассона): может быть описано следующей системой дифференциальных уравнений (схема Эйлера-Пуассона):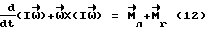 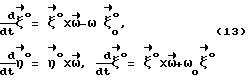 где I-diag (A,B,C) – тензор инерции ИСЗ в осях Cx,y,z). Назовем прямым положением равновесия ИСЗ в ОСК такое его положение, при котором оси X,Y,Z совпадают с осями  , , , , . В этом положении . В этом положении  1= 1=  2= 2=  3= 1, 3= 1, x= x=  z= 0, z= 0,  y= y=  o oПодставляя эти значения в (10) и (12), получим следующую алгебраическую систему относительно параметров -(vo  m m  -vc -vc m m  )yo+2vc )yo+2vc m m  zo= 0 zo= 0(vc  m m  -vc -vc m m  )xo+2vc )xo+2vc m m  zo= 0 zo= 0-2vc  m m  xo-2vc xo-2vc m m  yo= 0 yo= 0Эта система имеет решение 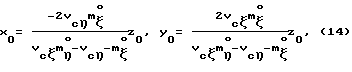 Z = const или: 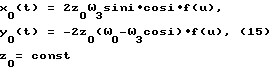 Z0 = const, где f(U) – известная на основании (5) функция: 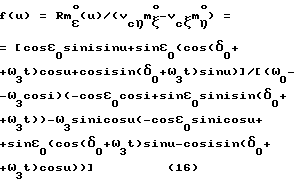 Следовательно, если координаты центра заряда на ИСЗ будут изменяться по закону (15), то ИСЗ будет иметь прямое положение равновесия в ОСК, при этом в углах ориентации  , ,  , ,  (“самолетные” углы – /2/) прямое положение равновесия определяется равенствами (“самолетные” углы – /2/) прямое положение равновесия определяется равенствами  = =  = =  = 0. = 0.Оценки показывают, что все координаты центра заряда X0, Y0, Z0 остаются ограниченными по модулю во все время движения. Так, в случае экваториальной орбиты (i=0) из формул (15) получаем: X0 = 0, 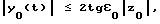 Z0 = const причем tg  0 0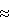 0,2035. 0,2035.В общем случае (i  0) знаменатель в выражении функции f(U) не обращается в нуль для орбит не выше геостационарной ( 0) знаменатель в выражении функции f(U) не обращается в нуль для орбит не выше геостационарной ( 0> 0> 3) при i < 78o и тем более при малых значениях i.
Существование решения (14) при наличии демпфирования в системе ИСЗ обеспечивает существование и асимптотическую устойчивость прямого положения равновесия, т.е. решает задачу стабилизации ИСЗ в ОСК.
При выполнении (14) проекции 3) при i < 78o и тем более при малых значениях i.
Существование решения (14) при наличии демпфирования в системе ИСЗ обеспечивает существование и асимптотическую устойчивость прямого положения равновесия, т.е. решает задачу стабилизации ИСЗ в ОСК.
При выполнении (14) проекции 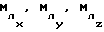 (11) восстанавливающего момента (11) восстанавливающего момента 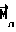 имеют вид имеют вид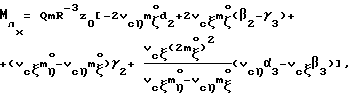 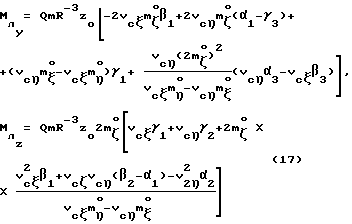 Пусть в системе ИСЗ имеется также демпфирующий момент 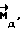 например, пропорциональный относительной угловой скорости ИСЗ в ОСК: например, пропорциональный относительной угловой скорости ИСЗ в ОСК: 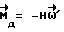 , где H = diag (h1, h2, h3), , где H = diag (h1, h2, h3),hi > 0 (i = 1,2,3), 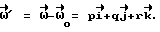 Тогда 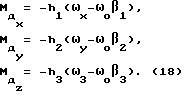 В окрестности прямого положения равновесия моменты 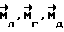 могут быть разложены в ряд по степеням малых величин могут быть разложены в ряд по степеням малых величин 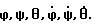 В результате получим их проекции в виде: В результате получим их проекции в виде:   где 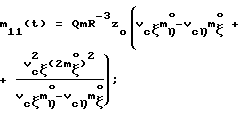 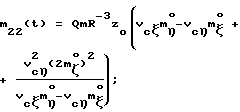 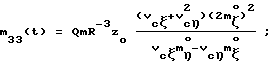 m13(t) = QmR-3zo2vc  m m  ; ;m23(t) = -QmR-3zo2vc  m m  ; ;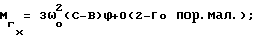 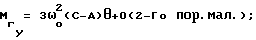 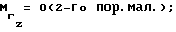 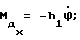 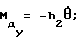 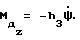 Динамические уравнения Эйлера 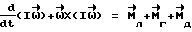 В матричной форме примут вид: 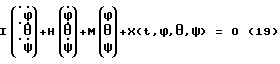 где 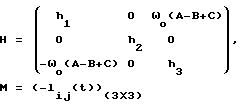 X(t,  , , , , ) – вектор с компонентами, содержащими нелинейные члены относительно ) – вектор с компонентами, содержащими нелинейные члены относительно  , , , , , а также члены 2-го и более высоких порядков относительно малого параметра sini. Таким образом, , а также члены 2-го и более высоких порядков относительно малого параметра sini. Таким образом, 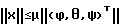 , где , где  – некоторая достаточно малая положительная постоянная. Компоненты mij матрицы M, зависящие от малого параметра sini, представим в виде суммы членов mij(0)(t), не зависящих от sini, и членов mij(1)(t), содержащих множителем sini. Тогда – некоторая достаточно малая положительная постоянная. Компоненты mij матрицы M, зависящие от малого параметра sini, представим в виде суммы членов mij(0)(t), не зависящих от sini, и членов mij(1)(t), содержащих множителем sini. Тогда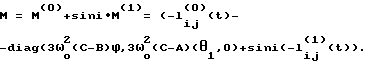 Рассмотрим систему линейного приближения уравнений (19) при i = 0: 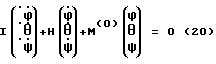 Здесь 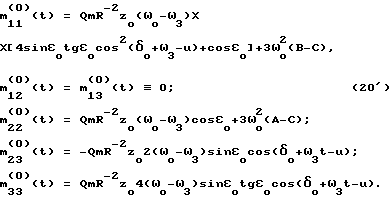 Представим mij(0)(t) в виде 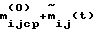 , где mijср(0) – среднее по t значение mij(0)(t).
Тогда , где mijср(0) – среднее по t значение mij(0)(t).
Тогда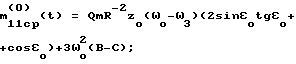 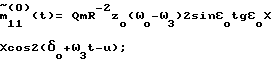 m22ср(0) = m22(0); m23ср(0) = 0; m(0)33cp= QmR-2zo  2( 2( o– o– 3)sin 3)sin otg otg o; o;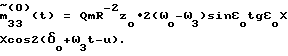 Рассмотрим дифференциальную систему 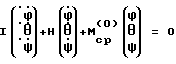 Поскольку Mср(0) > 0 при выполнении неравенства m11ср(0) > 0, m22ср(0) > 0, m33ср(0) > 0, то все решения этой дифференциальной системы обладают свойством асимптотической устойчивости. А так как 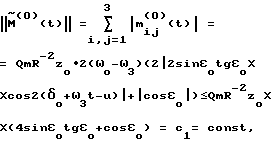 причем C1 зависит только от Mср(0), то и все решения дифференциальной системы (20) 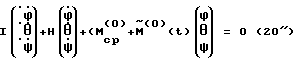 Обладают свойством асимптотической устойчивости, которая является равномерной, поскольку коэффициенты системы (20) периодичны по t. Из экспоненциальной асимптотической устойчивости нулевого решения системы (20) в силу неравенства 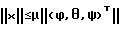 вытекает также экспоненциально-асимптотическая устойчивость нулевого решения исходной нелинейной системы (19) при i = 0/8/. А это доказывает возможность стабилизации ИСЗ в соответствии с изобретением для случая i=0.
В общем случае, для орбит малого наклонения (i вытекает также экспоненциально-асимптотическая устойчивость нулевого решения исходной нелинейной системы (19) при i = 0/8/. А это доказывает возможность стабилизации ИСЗ в соответствии с изобретением для случая i=0.
В общем случае, для орбит малого наклонения (i  0, но sini – мало) дифференциальные уравнения возмущенного движения (19) удобно записать в виде 0, но sini – мало) дифференциальные уравнения возмущенного движения (19) удобно записать в виде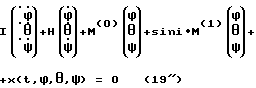 Согласно теореме об устойчивости при постоянно действующих возмущениях (п. д. в. ) /9/ равномерная асимптотическая устойчивость нулевого решения системы (20) является достаточным условием устойчивости этого решения при п. д.в. В качестве последних можно рассматривать малые по норме возмущения. Более того, поскольку дифференциальная система (20) является сильно устойчивой, то и линейное приближение системы (17) является также сильно устойчивым для достаточно малых значений i /8/. Следовательно, невозмущенное движение  = =  = =  = 0, описываемое исходной нелинейной системой (19), будет асимптотически устойчивым при достаточно малых значениях i /9/.
Таким образом, при выполнении соотношений (20′), которым должны удовлетворять заряд Q на ИСЗ и координаты центра заряда z0 в условиях гравитационных возмущений и демпфирования достигается устойчивость стабилизируемого прямого положения равновесия и асимптотическая устойчивость при достаточно малых значениях il, что служит обоснованием применения заявляемого способа для орбит малого наклонения.
Способ может быть осуществлен с помощью известных технических средств, позволяющих создать заряженный экран на поверхности ИСЗ. Величина суммарного заряда поверхности ИСЗ и расположение центра заряда относительно центра масс определяются вышеприведенными условиями и соотношениями (20′).
Для апробации способа при конкретных значениях параметров ИСЗ, орбиты и начальных условий движения было проведено численное моделирование. В качестве независимых квазикоординат, в которых записывалась система дифференциальных уравнений вращательного движения ИСЗ, были взяты параметры Родрига-Гамильтона и проекции угловой скорости ИСЗ на его главные центральные оси инерции (это позволяет избежать трудностей, связанных с вырождением кинематических уравнений при определенных значениях “самолетных” углов, а также с выполнением большого объема операций с тригонометрическими функциями от этих углов). Численное решение задачи Коши для построенной дифференциальной системы 7-го порядка производилось с помощью метода Рунге-Кутта-Фельдберга 4-5 порядков с автоматическим выбором шага, реализованного в системе MATLAB фирмы MathWorks.
При расчетах использованы следующие значения параметров (сохранены обозначения, введенные ранее в теоретическом обосновании способа): = 0, описываемое исходной нелинейной системой (19), будет асимптотически устойчивым при достаточно малых значениях i /9/.
Таким образом, при выполнении соотношений (20′), которым должны удовлетворять заряд Q на ИСЗ и координаты центра заряда z0 в условиях гравитационных возмущений и демпфирования достигается устойчивость стабилизируемого прямого положения равновесия и асимптотическая устойчивость при достаточно малых значениях il, что служит обоснованием применения заявляемого способа для орбит малого наклонения.
Способ может быть осуществлен с помощью известных технических средств, позволяющих создать заряженный экран на поверхности ИСЗ. Величина суммарного заряда поверхности ИСЗ и расположение центра заряда относительно центра масс определяются вышеприведенными условиями и соотношениями (20′).
Для апробации способа при конкретных значениях параметров ИСЗ, орбиты и начальных условий движения было проведено численное моделирование. В качестве независимых квазикоординат, в которых записывалась система дифференциальных уравнений вращательного движения ИСЗ, были взяты параметры Родрига-Гамильтона и проекции угловой скорости ИСЗ на его главные центральные оси инерции (это позволяет избежать трудностей, связанных с вырождением кинематических уравнений при определенных значениях “самолетных” углов, а также с выполнением большого объема операций с тригонометрическими функциями от этих углов). Численное решение задачи Коши для построенной дифференциальной системы 7-го порядка производилось с помощью метода Рунге-Кутта-Фельдберга 4-5 порядков с автоматическим выбором шага, реализованного в системе MATLAB фирмы MathWorks.
При расчетах использованы следующие значения параметров (сохранены обозначения, введенные ранее в теоретическом обосновании способа):m = 8,06  1022 A 1022 A  m2, m2,  3= 7,292123 3= 7,292123 10-5 1/c, 10-5 1/c, o= 11,5 o= 11,5 /180, /180,  o= 0, o= 0,   = 0, = 0,R = 7  106м, A = 103 кг 106м, A = 103 кг  м2, Q = 10(-3) Кл.
Значения остальных параметров i, м2, Q = 10(-3) Кл.
Значения остальных параметров i, , , ,z0,h (где h = H/A ,z0,h (где h = H/A o – безразмерный коэффициент демпфирования в выражении момента o – безразмерный коэффициент демпфирования в выражении момента 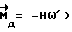 варьировались.
Для каждого набора значений параметров расчеты выполнялись по двум математическим моделям – соответственно при отсутствии и наличии управления ориентацией по предлагаемому способу (фиг. 2 и 3). Расчеты проведены для зависимостей “самолетных” углов ориентации ИСЗ от аргумента широты – безразмерной угловой величины u = варьировались.
Для каждого набора значений параметров расчеты выполнялись по двум математическим моделям – соответственно при отсутствии и наличии управления ориентацией по предлагаемому способу (фиг. 2 и 3). Расчеты проведены для зависимостей “самолетных” углов ориентации ИСЗ от аргумента широты – безразмерной угловой величины u =   + + ot на интервале 0 ot на интервале 0  U U  35, что соответствует 35/(2 35, что соответствует 35/(2 ) = 5,5 оборотам ИСЗ по орбите. На фиг. 2 и 3 сплошной линией показаны зависимость ) = 5,5 оборотам ИСЗ по орбите. На фиг. 2 и 3 сплошной линией показаны зависимость  = =  (u), пунктирной – (u), пунктирной –  = =  (u), точечной – (u), точечной –  = =  (u). (u).Сравнение расчетных графиков показывает, что введение в управление системой ориентации ИСЗ предлагаемого способа позволяет за короткое время достичь режима стабилизированного движения. При этом полностью отсутствует необходимость в установке гироскопов, маховиков и т.п., обеспечивающих стабилизацию положения ИСЗ, расходовании какого-либо рабочего вещества исполнительным механизмом. Очевидная простота закона управления, не требующего измерять какие-либо углы ориентации, их производные и пр. в процессе движения ИСЗ, надежность и экономичность способа свидетельствуют в пользу перспективности его использования для стабилизации ИСЗ. Предлагаемый способ может быть реализован путем создания системы электродов, имитирующих управляемый электростатический слой, который может быть как простым, так и двойным. В первом случае система может состоять из отдельных электродов, расположенных на внешней непроводящей поверхности ИСЗ и соединенных между собой через управляемые маломощные источники ЭДС, которые создают распределение заряда в соответствии с требуемым для данного способа законом управления положением центра заряда ИСЗ. Предполагается, что постоянный суммарный заряд ИСЗ поддерживается, например, с помощью электронного эмиттера. Во втором случае система электродов имитирует двойной электростатический слой на поверхности ИСЗ с управляемым распределением дипольного момента по поверхности ИСЗ. При этом необходимый для управления момент лоренцевых сил обеспечивается наличием на ИСЗ суммарного по поверхности дипольного момента двойного слоя, эквивалентного с точки зрения формулы изобретения простому электрическому слою с таким же дипольным моментом распределения заряда, равным Qz0, в приведенной формуле. Управление распределенным моментом осуществляется с помощью управляемых источников ЭДС так же как в предыдущем случае осуществлялось управление распределением заряда простого слоя. Источники информации: 1. Ландау Л.Д., Лифшиц Е.М. Теория поля, М., 1973. 2. Тихонов А.А. К вопросу о влиянии неоднородности геомагнитного поля на динамику экранированного тела. Л., 1987. 13 с. – Деп. в ВИНИТИ 04.08.87, N 5566 – B87. 3. Франция, заявка N 2550757, МКИ B 64 G 1/36 “Способ регулирования положения спутников”. 4. Мак-Илвейн Р.Дж. Изменение кинетического момента спутника при помощи магнитного поля земли. М., 1966. 5. Труханов К.А., Рябова Т.Я., Морозов Д.Х. Активная защита космических кораблей. М., 1970. 6. Лунев В. В., Вращательное движение заряженного твердого тела в магнитном поле. Автореферат диссертации. Л., 1979. 7. Белецкий В. В. Движение искусственного спутника относительно центра масс. М., 1965. 8. Якубович В.А., Старжинский В.М. Линейные дифференциальные уравнения с периодическими коэффициентами и их приложения. – М.: Наука, 1972. 9. Малкин И.Г. Теория устойчивости движения. – М.: Наука, 1966. Формула изобретения
QmR-2z0(  0– 0– 3)(2sin 3)(2sin 0tg 0tg 0+cos 0+cos 0)+3 0)+3 20(B-C) > 0, 20(B-C) > 0,QmR-2z0(  0– 0– 3)cos 3)cos 0+3 0+3 20(A-C) > 0, 20(A-C) > 0,Qmz0(  0– 0– 3) > 0, 3) > 0,где z0 – координата центра заряда ИСЗ относительно центра масс ИСЗ вдоль оси, совпадающей в положении равновесия с направлением местной вертикали; m – магнитный момент земного диполя; R – радиус орбиты ИСЗ;  0 – орбитальная угловая скорость центра масс ИСЗ; 0 – орбитальная угловая скорость центра масс ИСЗ; 3 – угловая скорость суточного вращения Земли; 3 – угловая скорость суточного вращения Земли; 0 0  11,5 11,5 – угол между осями магнитного диполя и суточного вращения Земли; – угол между осями магнитного диполя и суточного вращения Земли;A, B, C – главные центральные моменты инерции ИСЗ. РИСУНКИ
MM4A Досрочное прекращение действия патента Российской Федерации на изобретение из-за неуплаты в установленный срок пошлины за поддержание патента в силе
Дата прекращения действия патента: 30.10.2003
Извещение опубликовано: 27.12.2004 БИ: 36/2004
|
||||||||||||||||||||||||||
