Патент на изобретение №2158960
|
||||||||||||||||||||||||||
(54) СПОСОБ АВТОМАТИЧЕСКОГО РАСЧЕТА ФОРМЫ ОБЪЕМНЫХ ТЕЛ
(57) Реферат: Изобретение относится к робототехнике и может быть использовано в системах технического зрения для автоматического расчета формы объемных тел. Сущность изобретения заключается в том, что форма объемных тел определяется на основе полутоновой информации. Способ основывается на расчете ориентации элементарных площадок по яркостным поверхностям, сформированным по трем снимкам калибровочного и трем снимкам искомого объектов. Определение ориентации элементарных площадок искомого объекта базируется на предположении, что элементарные площадки с одинаковой яркостью на снимках искомого и калибровочного объектов имеют одинаковую ориентацию. Расчет ориентации элементарных площадок позволяет смоделировать плоские векторные поля, по которым можно определить сечения искомой поверхности, то есть рассчитать форму видимой части поверхности искомого объекта. Способ позволяет упростить определение формы объемных тел и повысить точность расчета. 1 з.п. ф-лы, 13 ил. Изобретение относится к таким областям техники, как робототехника, машинное зрение, системы технического зрения, искусственный интеллект. Известен способ для автоматического расчета формы объемных тел с применением средств технического зрения, основанный на структурном освещении. Данный способ позволяет достаточно точно автоматически рассчитывать форму объемных тел, для этого требуется специально структурированное освещение, которое достигается за счет использования всевозможных решеток и лазеров (см. а.с. СССР N 1621846, МК0И A 43 D 1/02; A 41 H 1/04, опублик. в БИ N 3, 1993; а. с. СССР N 1244481, МКИ G 01 B 11/24, опублик. в БИ N 26, 1986 г). Способ, основанный на структурном освещении, по сравнению с предложенным способом позволяет более точно рассчитывать форму объемных тел, однако у него имеются и недостатки. Они заключаются в том, что в случае использования решеток обеспечивается неплохая точность только на близком расстоянии из-за рассеивания света, а при использовании лазера для освещения объекта оборудование становится дорогостоящим. Из сказанного видно, что для реализации способа, основанного на структурном освещении, необходимо использовать дополнительное световое оборудование к СТЗ. Кроме того этот способ использует в своих алгоритмах информацию об источнике освещения и направленности световых лучей, что ограничивает зону рабочего пространства. Наиболее близким к предлагаемому техническому решению является способ автоматического расчета формы тел с использованием полутоновой информации, в котором координаты точек, принадлежащих сечениям поверхности искомого объекта, рассчитываются как линии тока плоского векторного поля, смоделированного по ориентации элементарных площадок искомой поверхности. При этом ориентация элементарных площадок поверхности определяется на основе ее яркости с использованием карты отражательной способности, (см. Хорн Б.К.П. Зрение роботов: Пер. с англ. М.: Мир, 1989. – 487 с. (стр. 251-270), Хорн Б., Минский М., Сираи И., Уолц Д., Уинстон П. Психология машинного зрения. М.: Мир, 1978. – 340 с). К недостаткам этого способа можно отнести тот факт, что при расчете формы тела смоделированное векторное поле не учитывает факт центрального проецирования. Оно принимается равным полю, сформированному при ортогональном проецировании. Это приводит к снижению точности расчета. Задача, решаемая в предлагаемом изобретении, заключается в разработке способа, позволяющего повысить точность расчета формы объемных тел по полутоновой информации. Для достижения указанного технического результата в способе автоматического расчета формы объемных тел, заключающийся в обработке полутоновой информации, полученной с помощью СТЗ, отличающийся тем что, для реализации способа необходимо иметь шесть яркостных поверхностей, сформированных по трем снимкам калибровочного и трем снимкам искомого объекта, при этом положения камеры и искомого объекта для всех снимков должны быть неизменными, т. е. искомый и калибровочный объекты должны находиться приблизительно в одном и том же месте и должны быть соизмеримы по размерам и иметь идентичную отражательную способность, этого можно добиться, используя материалы с одинаковой шероховатостью и покрыв их одинаковой краской, причем снимки калибровочного и искомого объектов снимаются попарно при одинаковых условиях освещения, а источники освещения для каждой пары снимков располагают в различных местах, и при этом методика автоматического расчета формы объемных тел по полутоновой информации предполагает наличие информации о положении в пространстве хотя бы одной точки его поверхности, а яркостные поверхности, сформированные по снимкам калибровочного и искомого объектов сглаживают с помощью аппроксимирующего сплайна (Носач В.В. Решение задач аппроксимации с помощью персональных компьютеров. – М. МИКАП, 1994. – 382 с.), причем координаты точек, принадлежащих сечениям поверхности искомого объекта, рассчитываются как линии тока плоского векторного поля, инцидентного центру проецирования (понятие инцидентность поясняется в книге Четверухина Н.Ф. Проективная геометрия. – М.: Просвещение, 1969. – 368 с. на с. 65), а векторное поле моделируется на базе информации по ориентации элементарных площадок искомой поверхности, ориентации самих элементарных площадок определяются по яркости точек на изображении, кроме того при моделировании векторного поля, определяющего сечение искомой поверхности, предлагается ввести корректировку, которая учитывает законы центрального проецирования, для чего предлагается в уравнении векторного поля y’ = f(x, y) провести замену: 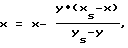 где xs, ys – координаты центра проецирования в плоскости векторного поля; x и у – координаты точек векторного поля, ось x направлена по линии пересечения картинной плоскости с секущей плоскостью, в которой рассчитывается сечение искомой поверхности, ось y расположена в секущей плоскости перпендикулярно оси x. Полученное таким образом векторное поле позволяет достичь технический результат, который выражается в повышении точности расчета формы искомого объекта. Из вышеизложенного видно, что заявляемый способ корректировки векторного поля в совокупности с известными техническими решениями обеспечивает простой, дешевый и достаточно точный способ автоматического расчета формы объемных тел. Это позволяет сделать вывод о том, что заявляемый способ образует единый изобретательский замысел. Анализ патентной научно-технической литературы показал, что из уровня техники неизвестны технические решения, содержащие совокупность признаков, сходных или эквивалентных заявляемому. Это позволяет сделать вывод о соответствии предложения критериям “новизна” и “изобретательский уровень”. Сущность изобретения поясняется чертежами, где: на фиг. 1 изображена фотография калибровочного шара; на фиг. 2 изображена рассчитанная видимая СТЗ поверхность шара; на фиг. 3 изображена несглаженная яркостная поверхность; на фиг. 4 изображена сглаженная яркостная поверхность; на фиг. 5 изображена общая схема автоматического расчета поверхности; на фиг. 6 изображена яркостная поверхность искомого объекта и определение яркости в точке T; на фиг. 7 изображено определение точек на яркостной поверхности калибровочного объекта, имеющих одинаковую яркость с точкой T – изофот; на фиг. 8 изображено определение точки пересечения изофот яркостных поверхностей калибровочного объекта; на фиг. 9 изображена функция касательных от X; на фиг. 10 изображено расчетное векторное поле касательных к искомой поверхности; на фиг. 11 изображена схема экспериментальной установки; на фиг. 12 изображена восстанавливаемая деталь; на фиг. 13 изображена восстановленная поверхность детали. Способ автоматического расчета формы объемных тел основывается на определении ориентации фрагментов поверхности по некоторому числу изображений, полученных при различных условиях освещенности с помощью яркостных поверхностей (фиг. 3). Яркостные поверхности полутоновых изображений формируются с помощью аналого-цифровых преобразователей. В силу наличия аппаратных погрешностей эти поверхности имеют, как правило, зубчатообразную форму (фиг. 3). Поэтому эти поверхности сглаживают математически (фиг. 4). Для этого можно использовать различные способы сглаживания, в частности, можно воспользоваться аппроксимирующим сплайном. Для определения ориентации элементарных площадок необходимо иметь шесть яркостных поверхностей, сформированных по трем снимкам калибровочного и трем снимкам искомого объектов. Положение камеры для всех снимков должно быть неизменным. Искомый и калибровочный объекты должны располагаться приблизительно в одном и том же месте, быть соизмеримы по размерам и иметь идентичную отражательную способность, т. е. должны быть покрыты одинаковой краской и иметь одинаковую шероховатость. Изображения калибровочного и искомого объектов снимаются попарно при одинаковых условиях освещения. Источники освещения для каждой пары снимков располагают из различных местах. Для упрощения процесса разъяснения, каким образом рассчитываются ориентации элементарных площадок искомого объекта, введем обозначения: три яркостные поверхности искомого объекта обозначим через Ri =  i(u, i(u, ), i = l…3, а три яркостные поверхности калибровочного объекта обозначим через Ri = ), i = l…3, а три яркостные поверхности калибровочного объекта обозначим через Ri = 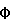 i(u, i(u, ), i = l..3. Здесь u, ), i = l..3. Здесь u, являются координатами точки на плоскости изображения в системе координат изображения u0 являются координатами точки на плоскости изображения в системе координат изображения u0 , R – яркость точки изображения, i – номер снимков искомого и калибровочного объектов, отснятых при одинаковых условиях освещения.
Для определения ориентации в некоторой точке T на искомой поверхности находится проекция этой точки T’ на плоскости изображения и по яркостным поверхностям искомого объекта Ri = , R – яркость точки изображения, i – номер снимков искомого и калибровочного объектов, отснятых при одинаковых условиях освещения.
Для определения ориентации в некоторой точке T на искомой поверхности находится проекция этой точки T’ на плоскости изображения и по яркостным поверхностям искомого объекта Ri =  i(uT, i(uT, T) (фиг. 6) определяются яркости этой точки на трех снимках. Обозначим эти яркости через RiT. Затем яркостные поверхности калибровочного объекта Ri = T) (фиг. 6) определяются яркости этой точки на трех снимках. Обозначим эти яркости через RiT. Затем яркостные поверхности калибровочного объекта Ri = 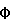 i(u, i(u, ) рассекаются плоскостями, ортогональными оси яркости и проходящими через соответствующие значения яркости RiT. Пересечением соответствующих поверхностей и плоскостей будут кривые li, (фиг. 7), которые, после ортогонального проецирования на плоскости изображения калибровочной сферы и совмещения полученных проекций (фиг. 8), в идеале должны иметь одну точку пересечения L’ (так как за калибровочный объект лучше всего брать шар, то его две замкнутые выпуклые изофоты пересекутся в двух точках, третья изофота будет проходить вблизи одной из них и эту точку следует принимать за точку пересечения изофот). Из этого следует, что на изображении калибровочной сферы найдена такая точка L’, значения яркостей в которой совпадают со значениями яркостей на снимках искомого объекта в точке T’. Образом точки L’ на калибровочном объекте будет точка L, ориентация которой легко рассчитывается. Так как элементарные площадки с одинаковой яркостью имеют одинаковую ориентацию, то ориентацию в точке T’ можно принять равной ориентации точки L. Действуя аналогичным образом, можно определить ориентацию элементарной площадки для любой точки изображения искомого объекта.
При автоматическом расчете формы поверхности по данному способу необходимо также иметь информацию о положении в пространстве хотя бы одной точки исследуемого объекта или должна быть возможность ее определения. Эту точку обозначим через M (фиг. 5).
Для автоматического расчета формы поверхности берут пучок плоскостей с осью, проходящей через фокус объектива камеры S, и известную точку M искомого объекта (фиг. 5).
Этот пучок плоскостей будет рассекать искомую поверхность по кривым, а плоскость изображения по прямым. Рассмотрим одну плоскость из этого пучка, обозначим ее Г. Введем в этой плоскости систему координат: за ось абсцисс примем линию пересечения плоскости Г с плоскостью изображения ) рассекаются плоскостями, ортогональными оси яркости и проходящими через соответствующие значения яркости RiT. Пересечением соответствующих поверхностей и плоскостей будут кривые li, (фиг. 7), которые, после ортогонального проецирования на плоскости изображения калибровочной сферы и совмещения полученных проекций (фиг. 8), в идеале должны иметь одну точку пересечения L’ (так как за калибровочный объект лучше всего брать шар, то его две замкнутые выпуклые изофоты пересекутся в двух точках, третья изофота будет проходить вблизи одной из них и эту точку следует принимать за точку пересечения изофот). Из этого следует, что на изображении калибровочной сферы найдена такая точка L’, значения яркостей в которой совпадают со значениями яркостей на снимках искомого объекта в точке T’. Образом точки L’ на калибровочном объекте будет точка L, ориентация которой легко рассчитывается. Так как элементарные площадки с одинаковой яркостью имеют одинаковую ориентацию, то ориентацию в точке T’ можно принять равной ориентации точки L. Действуя аналогичным образом, можно определить ориентацию элементарной площадки для любой точки изображения искомого объекта.
При автоматическом расчете формы поверхности по данному способу необходимо также иметь информацию о положении в пространстве хотя бы одной точки исследуемого объекта или должна быть возможность ее определения. Эту точку обозначим через M (фиг. 5).
Для автоматического расчета формы поверхности берут пучок плоскостей с осью, проходящей через фокус объектива камеры S, и известную точку M искомого объекта (фиг. 5).
Этот пучок плоскостей будет рассекать искомую поверхность по кривым, а плоскость изображения по прямым. Рассмотрим одну плоскость из этого пучка, обозначим ее Г. Введем в этой плоскости систему координат: за ось абсцисс примем линию пересечения плоскости Г с плоскостью изображения  и обозначим ее через t’, за ось ординат можно принять любую прямую, перпендикулярную оси абсцисс и инцидентную секущей плоскости Г (на этой фигуре расчетная плоскость изображения и обозначим ее через t’, за ось ординат можно принять любую прямую, перпендикулярную оси абсцисс и инцидентную секущей плоскости Г (на этой фигуре расчетная плоскость изображения  располагается перед объективом, этим приемом пользуются многие разработчики систем технического зрения т.к. это позволяет существенно упростить выполнение математических операций (Дуда P., Харт П. Распознавание образов и анализ сцен. – М.: Мир, 1976. – 512 с.). Эта плоскость пересечет искомую поверхность по кривой t и плоскость изображения располагается перед объективом, этим приемом пользуются многие разработчики систем технического зрения т.к. это позволяет существенно упростить выполнение математических операций (Дуда P., Харт П. Распознавание образов и анализ сцен. – М.: Мир, 1976. – 512 с.). Эта плоскость пересечет искомую поверхность по кривой t и плоскость изображения  по прямой t’. Возьмем точку T’ на изображении объекта, инцидентную плоскости Г и плоскости по прямой t’. Возьмем точку T’ на изображении объекта, инцидентную плоскости Г и плоскости  . Если провести проецирующую прямую через точки T’ и S, то эта прямая пересечет искомую поверхность в точке T. По имеющейся информации можно определить касательную в точке T, базируясь на информации яркостей в точке T’. Следовательно, будет известно значение первой производной кривой t в точке T. Так как координаты точки T неизвестны, а координаты точки T’ изображения можно вычислить, то временно припишем значение первой производной точке T’. Взяв последовательность точек вдоль линии t’, расположенных достаточно близко друг от друга, определим первые производные в этих точках. Используя эту информацию, можно установить зависимость вида y’ = f(x) (фиг. 9).
Для ее установления можно проинтерполировать сплайн функцией третьего порядка полученный массив точек. Тогда эта зависимость между двумя смежными точками будет записываться в следующем виде . Если провести проецирующую прямую через точки T’ и S, то эта прямая пересечет искомую поверхность в точке T. По имеющейся информации можно определить касательную в точке T, базируясь на информации яркостей в точке T’. Следовательно, будет известно значение первой производной кривой t в точке T. Так как координаты точки T неизвестны, а координаты точки T’ изображения можно вычислить, то временно припишем значение первой производной точке T’. Взяв последовательность точек вдоль линии t’, расположенных достаточно близко друг от друга, определим первые производные в этих точках. Используя эту информацию, можно установить зависимость вида y’ = f(x) (фиг. 9).
Для ее установления можно проинтерполировать сплайн функцией третьего порядка полученный массив точек. Тогда эта зависимость между двумя смежными точками будет записываться в следующем видеy’1 = a0j + a1j*x + a2j*x2 + a3j*x3, (1) где a0j, a1j, a2j, a3j – коэффициенты интерполирующих сплайнов, j – номер интерполирующей дуги. Но эти функции позволяют верно рассчитать наклоны касательных только вдоль линии t’ плоскости Г. Учитывая факт центрального проецирования, можно утверждать, что величины первых производных будут постоянны вдоль проецирующих лучей. Тогда, чтобы установить зависимость y’ = f(x, y), для центрального проецирования, необходимо решить систему уравнений, позволяющую правильно определять наклоны касательных вдоль проецирующих лучей: 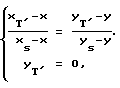 (2) (2)где x и y – произвольные координаты плоскости Г, xT’, и yT’ – координаты точки, инцидентной оси абсцисс и проецирующему лучу, проходящему через точку (x, y). Решив эту систему, можно получить выражение, определяющее координату xT’ через координаты произвольной плоскости Г 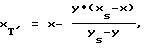 (3) (3)подставив выражение (3) в уравнение (1) можно получить уравнение векторного поля в виде y’ = f(x, y), которое уже учитывает равенство ориентации элементарных площадок вдоль проецирующих лучей 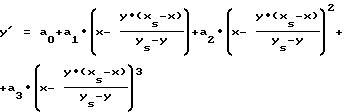 (4) (4)Для решения этого дифференциального уравнения (4) можно воспользоваться методом Рунге-Кутта. Для численного интегрирования известны начальные условия – это координаты точки М и направление прямой t’ на плоскости изображения  . Пусть величина h – размер шага интегрирования. Уравнение для производных в общем виде можно представить: . Пусть величина h – размер шага интегрирования. Уравнение для производных в общем виде можно представить:y’ = F(x, y) Формулы метода Рунге-Кутта на n-ом шаге имеют вид: K1 = h  F(Xn,Yn) F(Xn,Yn)K2 = h  F(Xn + h/2, Yn + K1/2) F(Xn + h/2, Yn + K1/2)K3 = h  F(Xn + h/2, Yn + K2/2) F(Xn + h/2, Yn + K2/2)K4 = h  F(Xn + h, Yn + K3) F(Xn + h, Yn + K3)Yn + 1 = Yn + (1/6)  (K1 + 2 (K1 + 2 K2 + 2 K2 + 2 K3 + K4) K3 + K4)После того как будут перебраны все точки вдоль прямой t’, рассчитаем кривую t. Перебрав с определенным шагом все плоскости Г из пучка плоскостей, можно сформировать каркас точек, инцидентных рассчитываемой поверхности. Реализация предложенного выше способа на компьютерах, состыкованных с оборудованием технического зрения, позволит создать установку, позволяющую рассчитывать видимую часть поверхности объекта по полутоновым изображениям. Данный способ может применяться в робототехнических комплексах для расчета формы и распознавания объектов. Пример конкретного выполнения способа. Для выполнения данного способа было использовано оборудование, показанное на фиг. 11, искомый объект (поз. 1), телевизионная камера КТП-82 (поз. 2), видеосканер VS-9 (поз. 3), компьютер IBM PC (поз. 4) и три точечных источника освещения (поз. 5, 6, 7). Искомым объектом является шар с диам. 160 мм (фиг. 1). Дистанция, с которой проводились съемки, равнялась 1500 мм. Телевизионная камера КТП-82 производства п/я М5460 1987 г. изготовления. Видеосканер VS-9 производства МНПО “СПЕКТР” Москва 1991 г. изготовления и его технические характеристики: размер изображения 256х256 пикселов с 256 уровнями интенсивности. Для автоматического расчета формы объекта (поз. 1) необходимо три раза сфотографировать объект, каждый раз поочередно включая один из источников освещения (поз. 5, 6, 7). Съемка объекта осуществляется следующим образом: телевизионную камеру (поз. 2) направляем на искомый объект (поз. 1), видеосигнал из камеры идет в видеосканер (поз. 3), после него оцифрованное изображение поступает в компьютер (поз. 4), где обрабатывается и получается рассчитанная поверхность. Для определения точности восстановления объемных тел данным способом был использован другой шар. Это объясняется легкостью расчета положения его координат точек. Автоматически рассчитанная поверхность шара (фиг. 2) имела погрешности (см. таблицу в конце текста). Пример практического использования, данного способа по восстановлению формы объемного тела (фиг. 12) приведен на фиг. 13. Использование предлагаемого способа по сравнению с прототипом позволяет обеспечить следующие преимущества: – повысить точность определения ориентации элементарных площадок и точность расчета формы искомого объекта; – отпала необходимость в использовании дополнительного оборудования (специальные решетки, лазеры) для освещения предметов. Формула изобретения
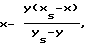 где xs, ys – координаты центра проецирования в плоскости векторного поля; x и y – координаты точек векторного поля, где ось x направлена по линии пересечения плоскости изображения с секущей плоскостью, в которой рассчитывают сечение поверхности искомого объекта, ось y расположена в секущей плоскости перпендикулярно оси x. 2. Способ по п.1, отличающийся тем, что искомый объект и калибровочный объект покрыты одинаковой краской и имеют одинаковую шероховатость. РИСУНКИ
MM4A – Досрочное прекращение действия патента СССР или патента Российской Федерации на изобретение из-за неуплаты в установленный срок пошлины за поддержание патента в силе
Дата прекращения действия патента: 25.02.2009
Извещение опубликовано: 20.05.2010 БИ: 14/2010
|
||||||||||||||||||||||||||
