Патент на изобретение №2306592
|
||||||||||||||||||||||||||
(54) СПОСОБ АКТИВНОЙ ИДЕНТИФИКАЦИИ ЛИНЕЙНЫХ ОБЪЕКТОВ УПРАВЛЕНИЯ
(57) Реферат:
Изобретение относится к идентификации объектов управления при неизвестных ограниченных внешних возмущениях, может быть использовано для определения математической модели объекта на основе дискретной информации о сигнале на его выходе и реализовано с применением ЭВМ в автоматическом режиме, в реальном масштабе времени. Технический результат заключается в повышении точности идентификации. Способ заключается в том, что испытательные гармоники подаются на вход объекта последовательно во времени, при этом каждой гармонике, действующей в течение рабочего интервала, предшествует интервал (интервал – пауза), на котором испытательный сигнал отсутствует. Интервалы – паузы и рабочие интервалы позволяют оценить влияние реализовавшегося внешнего возмущения на ошибку идентификации и уменьшить это влияние путем увеличения времени идентификации.
Изобретение относится к идентификации объектов управления при неизвестных ограниченных внешних возмущениях. Способ может быть применен для определения математической модели объекта на основе дискретной информации о сигнале на его выходе и реализован с применением ЭВМ в автоматическом режиме, в реальном масштабе времени. Известны способы идентификации линейных объектов управления (см. патент РФ RU (11) 2079870, кл. G05В 23/02, 1997 и патент РФ RU (11) 2146063, кл. G05В 17/02, 2000). Они не достигают цели, когда внешние возмущения, действующие на объект, неизвестны. 1. К асимптотически устойчивому объекту, описываемому уравнением прикладывается испытательный сигнал Здесь y(k) – измеряемый в момент hk (k=1, 2…); h – интервал дискретности измерений выхода объекта; f(k) – неизмеряемое неизвестное ограниченное внешнее возмущение: |f(k)| Амплитуды pi и частоты 2. Выход объекта прикладывается ко входам фильтра Фурье 3. Выходы фильтра Фурье служат коэффициентами следующей системы линейных алгебраических уравнений решение которых дает оценки Длительность идентификации в которых Недостатком этого способа является то, что при выполнении неравенств (5) длительность идентификации может оказаться недостаточной и оценка коэффициентов объекта будут существенно отличаться от их истинных значений. Целью изобретения является повышение точности определения времени идентификации, что приведет к уменьшению ошибок идентификации (разности абсолютных значений оценок коэффициентов объекта и их истинных величин). Поставленная цель достигается тем, что испытательные гармоники подаются на вход объекта не одновременно (параллельно), как в (2), а последовательно во времени. При этом каждой гармонике, действующей в течение рабочего интервала, предшествует интервал (интервал – пауза), на котором испытательный сигнал отсутствует. Интервалы – паузы и рабочие интервалы позволяют оценить влияние реализовавшегося внешнего возмущения на ошибку идентификации и уменьшить это влияние путем увеличения времени идентификации. Способ заключается в следующем. А). Процесс определения длительности идентификации состоит из интервалов [t[0], t[1]], [t[1], t[2]],…, [t[n-1], t[n]]. На i-м ( где Далее для простоты будем рассматривать лишь первый интервал (и поэтому верхние индексы в обозначениях (6) будем опускать). Он состоит из равных по длительности пар подинтервалов. На подинтервалах – паузах [t0, t1], [t2, t3],… испытательный сигнал отсутствует (u=0), а на рабочих подинтервалах – [t1, t2], [t3, t4],… – испытательный сигнал u(t)=p1sin В). Выходы фильтра Фурье (3) дают на подинтервалах [t0, t1] и [t1, t2] числа где Если выполняется условие
где В противном случае переходим ко второй паре подинтервалов ([t2, t3] и [t3, t4]), когда в (6) i=1, а q=2, и проверяем выполнение условий (8). Если они выполняются, то переходим ко второму интервалу (когда в (6) i=2), в противном случае переходим к третьей паре подинтервалов, когда в (6) i=1, а q=3 и т.д. до тех пор, пока не найдется число С). Подставляя эти числа в уравнения (4), найдем оценки искомых коэффициентов объекта (1).
Формула изобретения
Способ активной идентификации линейных объектов управления путем определения значений выходного сигнала объекта, на вход которого подают испытательный сигнал, приложения выходного сигнала к фильтру Фурье с последующим вычислением оценок коэффициентов объекта, отличающийся тем, что испытательные гармоники подают на вход объекта последовательно во времени так, что для каждой гармоники, действующей в течение рабочего интервала, которому предшествует интервал – пауза, где испытательный сигнал отсутствует, и для каждой пары интервалов находят числа
где
где где di, bi,
|
||||||||||||||||||||||||||

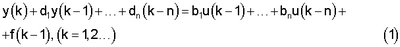
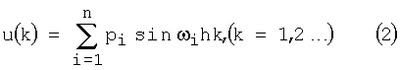
 f*, (k=1, 2…), f* – число, di, bi, (
f*, (k=1, 2…), f* – число, di, bi, (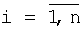 ) – неизвестные числа, n – известно.
) – неизвестные числа, n – известно. i (
i (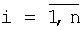 ) испытательного сигнала (2) – задаются.
) испытательного сигнала (2) – задаются.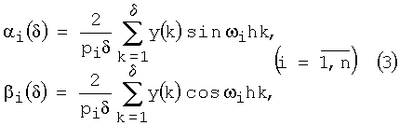
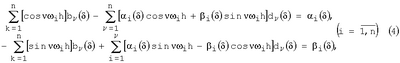
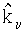 и
и 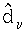 (
( h определяется из неравенств
h определяется из неравенств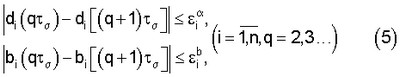
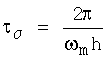 ,
, 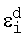 и
и 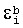 (
(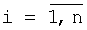 ) интервале испытательный сигнал
) интервале испытательный сигнал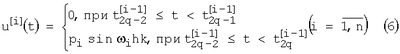
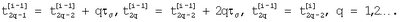
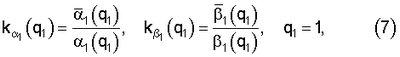
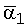 и
и 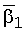 – значения выходов фильтра Фурье (3) при i=1,
– значения выходов фильтра Фурье (3) при i=1,  =0,
=0, 
 ,
,  1 и
1 и  1 – значения этих выходов при
1 – значения этих выходов при 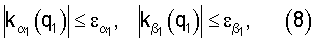
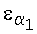 и
и 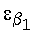 – заданные достаточно малые числа, то переходим ко второму интервалу, когда в (6) i=2.
– заданные достаточно малые числа, то переходим ко второму интервалу, когда в (6) i=2.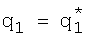 , при котором выполняются неравенства (8). Повторяем изложенное для случая, когда в (6) i=2 и т.д., и таким образом получим числа
, при котором выполняются неравенства (8). Повторяем изложенное для случая, когда в (6) i=2 и т.д., и таким образом получим числа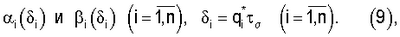
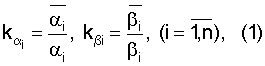
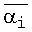 и
и 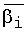 – значения выходов фильтра Фурье на интервале-паузе,
– значения выходов фильтра Фурье на интервале-паузе, 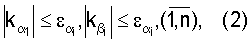
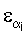 и
и 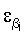 – заданные достаточно малые числа, то переходят к следующей гармонике, в противном случае увеличивают длительности рабочего интервала и интервала-паузы до тех пор, пока не выполнится условие (2) и затем находят оценки коэффициентов объекта управления путем решения системы линейных алгебраических уравнений
– заданные достаточно малые числа, то переходят к следующей гармонике, в противном случае увеличивают длительности рабочего интервала и интервала-паузы до тех пор, пока не выполнится условие (2) и затем находят оценки коэффициентов объекта управления путем решения системы линейных алгебраических уравнений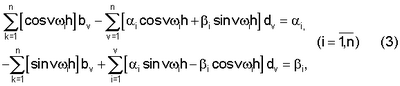
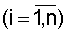 – искомые коэффициенты объекта;
– искомые коэффициенты объекта; 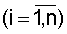 частоты испытательного сигнала; h – интервал дискретности.
частоты испытательного сигнала; h – интервал дискретности.