|
(21), (22) Заявка: 2005125378/09, 09.08.2005
(24) Дата начала отсчета срока действия патента:
09.08.2005
(43) Дата публикации заявки: 20.02.2007
(46) Опубликовано: 27.06.2007
(56) Список документов, цитированных в отчете о
поиске:
Шебшаевич В.С. и др. Сетевые спутниковые радионавигационные системы. – М.: Радио и Связь, 1993. RU 2204145 С2, 10.05.2003. JP 2000304854, 02.11.2000. JP 10111351, 28.04.1998.
Адрес для переписки:
197372, Санкт-Петербург, Богатырский пр-т, 53, корп.3, кв.283, И.Е.Зайцеву
|
(72) Автор(ы):
Голубев Валентин Анатольевич (RU),
Зайцев Игорь Евгеньевич (RU),
Сайбель Алексей Геннадиевич (RU),
Ушаков Борис Алексеевич (RU)
(73) Патентообладатель(и):
ЗАО “Региональный научно-исследовательский экспертный центр” (RU)
|
(54) СПОСОБ ПОДГОТОВКИ ИСХОДНЫХ ДАННЫХ РАЗНОСТНО-ДАЛЬНОМЕРНОЙ НАВИГАЦИОННОЙ ЗАДАЧИ
(57) Реферат:
Изобретение относится к области радиотехники и может быть использовано в разностно-дальномерных системах определения местоположения (ОМП) источников радиоизлучений (ИРИ). Технический результат заключается в уменьшении объема хранимых и передаваемых данных. Способ основан на измерении двух разностей дальностей  r12 и r12 и  r13 от ИРИ до двух пар подвижных опорных точек {O1,О2} и {О1,О3}, координат r13 от ИРИ до двух пар подвижных опорных точек {O1,О2} и {О1,О3}, координат 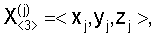 j=1, 2, 3 опорных точек Oj в момент времени измерения разностей дальностей, далее преобразуют вектор измеренных значений j=1, 2, 3 опорных точек Oj в момент времени измерения разностей дальностей, далее преобразуют вектор измеренных значений 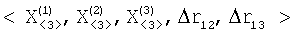 в вектор в вектор 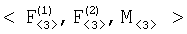 координат трех точек F1, F2 и М, принадлежащих гиперболине; вектор координат трех точек F1, F2 и М, принадлежащих гиперболине; вектор 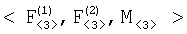 хранят и передают по каналам передачи информации в центр обработки информации для использования в качестве исходных данных при решении разностно-дальномерной навигационной задачи; при этом точки F1, и F2 определяют фокусы гиперболины, если она является гиперболой или эллипсом, или фокуса и его проекции на директрису, если она является параболой, а третья точка принадлежит гиперболине таким образом, что положение ее проекции на прямую F1F2 определяет вид кривой второго порядка. 4 ил. хранят и передают по каналам передачи информации в центр обработки информации для использования в качестве исходных данных при решении разностно-дальномерной навигационной задачи; при этом точки F1, и F2 определяют фокусы гиперболины, если она является гиперболой или эллипсом, или фокуса и его проекции на директрису, если она является параболой, а третья точка принадлежит гиперболине таким образом, что положение ее проекции на прямую F1F2 определяет вид кривой второго порядка. 4 ил.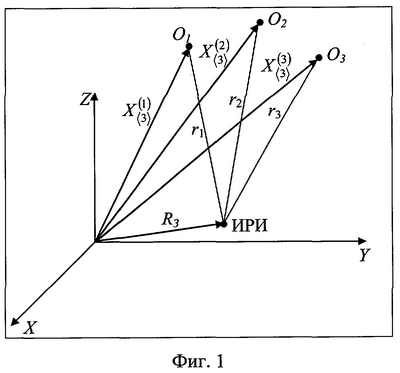
Данное предложение относится к области радиотехники и может быть использовано в разностно-дальномерных системах определения местоположения (ОМП) источников радиоизлучений (ИРИ) для уменьшения объема хранимых и передаваемых данных о результатах измерений, необходимых для вычисления координат ИРИ.
Разностно-дальномерные системы являются многопозиционными системами ОМП ИРИ [1]. Для измерения разности дальностей в РДМ системах ОМП используются различные способы: фазовый, частотный и временной [2].
Известны способы и устройства ОМП на основе РДМ метода [1-11 и другие].
Одним из видов РДМ систем ОМП являются многоспутниковые космические системы [например, 4], в которых роль опорных точек играют космические аппараты (КА). При этом разделяют системы, использующие для ОМП ИРИ группы из трех и четырех КА.
Система из трех КА позволяет определять координаты ИРИ, расположенных на поверхности Земли, а система из четырех КА позволяет определять координаты ИРИ, расположенных как на поверхности Земли, так и на летно-подъемных средствах (в пространстве).
Примерами космических РДМ систем, использующими группировки из трех КА, являются Уайт Клауд (США) [12], Рой (Франция) [13].
В этих системах сигнал наземного ИРИ принимается тремя КА, что дает возможность измерить разности дальностей от ИРИ до двух пар КА путем измерения разностей времен приема сигнала.
Алгоритм вычисления координат ИРИ сводится к определению точек пересечения двух гиперболоидов, задаваемых разностно-дальномерными измерениями, и поверхности Земли [4].
Исходная система уравнений имеет вид
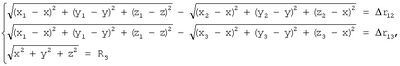
где  r1j=r1-rj, j=2, 3 – разность расстояний от пары опорных точек {O1,Oj} до ИРИ, r1j=r1-rj, j=2, 3 – разность расстояний от пары опорных точек {O1,Oj} до ИРИ,
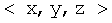 – вектор искомых координат ИРИ в геоцентрической системе координат XYZ (ГЦСК [2]), – вектор искомых координат ИРИ в геоцентрической системе координат XYZ (ГЦСК [2]),
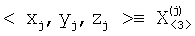 – вектор координат j-ой опорной точки в ГЦСК (взаимное расположение опорных точек и ИРИ в ГЦСК показано на фиг.1). – вектор координат j-ой опорной точки в ГЦСК (взаимное расположение опорных точек и ИРИ в ГЦСК показано на фиг.1).
Для решения данной системы уравнений необходимы исходные данные в виде значений двух разностей дальностей  r12 и r12 и  r13, координат опорных точек (координат КА в момент измерения r13, координат опорных точек (координат КА в момент измерения  rij), а также значения локального радиуса Земли RЗ в точке расположения ИРИ. rij), а также значения локального радиуса Земли RЗ в точке расположения ИРИ.
Таким образом, вектор исходных данных для решения РДМ навигационной задачи состоит из 12 скалярных величин: 9 координат трех КА 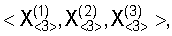 двух значений разностей дальностей двух значений разностей дальностей 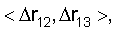 а также значения RЗ. При этом а также значения RЗ. При этом 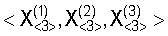 и и 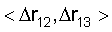 являются результатами измерений, a RЗ относится к априорно задаваемым исходным данным. Для грубых расчетов координат ИРИ значение RЗ может приниматься равным среднему радиусу земного шара. Для более точного ОМП ИРИ используют итеративную процедуру, суть которой состоит в следующем. На первом шаге в качестве значения RЗ принимается некоторая оценка являются результатами измерений, a RЗ относится к априорно задаваемым исходным данным. Для грубых расчетов координат ИРИ значение RЗ может приниматься равным среднему радиусу земного шара. Для более точного ОМП ИРИ используют итеративную процедуру, суть которой состоит в следующем. На первом шаге в качестве значения RЗ принимается некоторая оценка 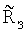 (например, среднее значение радиуса Земли); в результате решения системы уравнений определяются координаты ИРИ, и значение локального радиуса Земли в точке с полученными координатами используется для повторного решения исходной системы уравнений с целью уточнения координат. (например, среднее значение радиуса Земли); в результате решения системы уравнений определяются координаты ИРИ, и значение локального радиуса Земли в точке с полученными координатами используется для повторного решения исходной системы уравнений с целью уточнения координат.
В [4] описан способ подготовки исходных данных для решения РДМ навигационной задачи, который включает следующие операции:
– измеряют разности дальностей  r12 и r12 и  r13 от ИРИ до пар подвижных опорных точек {О1, O2} и {O1,O3}; r13 от ИРИ до пар подвижных опорных точек {О1, O2} и {O1,O3};
– измеряют координаты 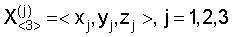 опорных точек Oj в момент времени измерения разностей дальностей; опорных точек Oj в момент времени измерения разностей дальностей;
– вектор измеренных значений 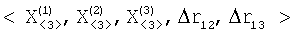 хранят и передают по каналам передачи информации в центр обработки информации для использования в качестве исходных данных при решении навигационной задачи (определении координат ИРИ). хранят и передают по каналам передачи информации в центр обработки информации для использования в качестве исходных данных при решении навигационной задачи (определении координат ИРИ).
При этом возможны различные варианты получения исходных данных для решения РДМ навигационной задачи:
– значения 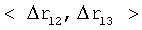 определяются на борту одного из КА группировки (например, КА2, см. фиг.2а); определяются на борту одного из КА группировки (например, КА2, см. фиг.2а);
– значения 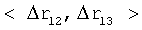 определяются в пункте приема информации (ППИ) (см. фиг.2б); определяются в пункте приема информации (ППИ) (см. фиг.2б);
– значения 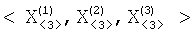 определяются наземными средствами измерения параметров движения КА; определяются наземными средствами измерения параметров движения КА;
– значения 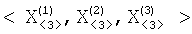 определяются бортовыми средствами КА. определяются бортовыми средствами КА.
В силу того, что КА могут находиться в зоне радиовидимости ППИ и наземных средств измерения ограниченное время, то наиболее целесообразным является вариант, когда значения 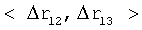 и и 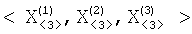 определяются бортовыми средствами КА и передаются на ППИ периодически (при появлении возможности) в виде множества одиннадцатикомпонентных векторов исходных данных навигационной задачи, при этом каждый вектор соответствует результатам наблюдения одного ИРИ. определяются бортовыми средствами КА и передаются на ППИ периодически (при появлении возможности) в виде множества одиннадцатикомпонентных векторов исходных данных навигационной задачи, при этом каждый вектор соответствует результатам наблюдения одного ИРИ.
Данный способ выбран в качестве прототипа.
Недостатком описанного способа является необходимость хранения и передачи по радиолинии КА-ППИ значительного объема данных.
Целью изобретения является снижение объема хранимых и передаваемых данных за счет замены одиннадцатикомпонентного вектора исходных данных эквивалентным ему по содержащейся информации вектором меньшей размерности.
Поставленная цель достигается тем, что вектор исходных данных РДМ навигационной задачи, содержащий значения координат трех опорных точек (O1,O2,O3) и двух разностей дальностей от ИРИ до двух пар этих опорных точек, обрабатывается, и вычисляются параметры пространственной кривой, являющейся пересечением двух гиперболических поверхностей положения ИРИ, соответствующих значениям  r12 и r12 и  r13 при заданных значениях r13 при заданных значениях 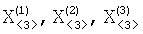 (гиперболины [14, 15]). (гиперболины [14, 15]).
Предлагаемый способ предполагает выполнение следующих операций:
– измеряют разности дальностей  r12 и r12 и  r13 от ИРИ до пар подвижных опорных точек {O1,O2} и {O1,O3}; r13 от ИРИ до пар подвижных опорных точек {O1,O2} и {O1,O3};
– измеряют координаты 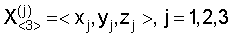 опорных точек Oj в момент времени измерения разностей дальностей; опорных точек Oj в момент времени измерения разностей дальностей;
– преобразуют вектор измеренных значений 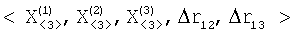 в вектор в вектор 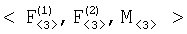 координат трех точек, принадлежащих гиперболине; координат трех точек, принадлежащих гиперболине;
– вектор 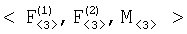 хранят и передают по каналам передачи информации в центр обработки информации для использования в качестве исходных данных при решении навигационной задачи (определении координат ИРИ). хранят и передают по каналам передачи информации в центр обработки информации для использования в качестве исходных данных при решении навигационной задачи (определении координат ИРИ).
Принцип, лежащий в основе предлагаемого способа, состоит в следующем.
Для удобства и наглядности дальнейшего изложения введем в рассмотрение систему координат Oxyz, заданную таким образом, что ее начало совпадает с серединой отрезка O1O2, ось Ох коллинеарна вектору 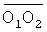 , а плоскость хОу совпадает с плоскостью O1O2O3 (см. фиг.3). Тогда в системе Oxyz O1(-а,0,0), O2(а,0,0} и O3(x3,y3,0), , а плоскость хОу совпадает с плоскостью O1O2O3 (см. фиг.3). Тогда в системе Oxyz O1(-а,0,0), O2(а,0,0} и O3(x3,y3,0),
где а=|O1O2|/2,
х3=(b2-с2)/a,
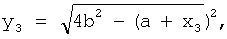
b=|O1O3|/2,
c=|O2O3|/2,
и, следовательно, можно записать
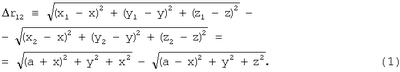
Возведя в квадрат правую и левую части уравнения (1), получим
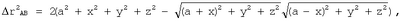
а следовательно,
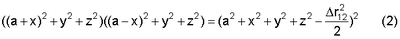
Если раскрыть скобки в левой части и произвести упрощения, то уравнение (2) примет вид канонического уравнения двуполостного гиперболоида вращения
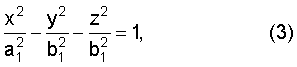
где 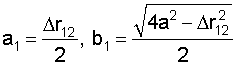
Таким образом, из приведенных выше рассуждений следует, что точка расположения ИРИ принадлежит поверхности, описываемой уравнением (3).
Аналогично, введя в рассмотрение систему координат О’х’у’z’, начало которой совпадает с серединой отрезка O1O3, ось O’х’ коллинеарна вектору 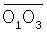 , а плоскость х’O’у’ совпадает с плоскостью O1O2O3, можно получить, что точка расположения ИРИ принадлежит поверхности, описываемой уравнением , а плоскость х’O’у’ совпадает с плоскостью O1O2O3, можно получить, что точка расположения ИРИ принадлежит поверхности, описываемой уравнением
 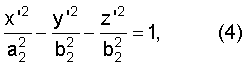
где 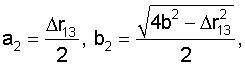
x’,y’,z’ – координаты ИРИ в системе координат O’x’y’z’.
Поскольку точка расположения ИРИ принадлежит одновременно двум поверхностям, следовательно, она принадлежит линии пересечения этих поверхностей.
С другой стороны, гиперболоид определяется своим фокусом, директориальной плоскостью и эксцентриситетом [16]
r=s·d,
где r – расстояние от точки гиперболоида до фокуса;
d – расстояние от точки гиперболоида до директориальной плоскости;
 >1 – эксцентриситет (фиксированная величина). >1 – эксцентриситет (фиксированная величина).
Следовательно, линия пересечения двух гиперболоидов с общим фокусом (гиперболина) описывается системой уравнений
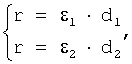
где r – расстояние от точек гиперболины до общего фокуса.
Следовательно
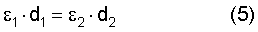
Уравнение (5) представляет уравнение плоскости. Следовательно, все точки гиперболины принадлежат одной плоскости, описываемой уравнением (5). Поскольку все точки гиперболины одновременно принадлежат и гиперболоиду вращения, следовательно, гиперболина является кривой второго порядка (другое, более очевидное, доказательство данного факта приведено в [15]).
Следовательно, вектор исходных данных 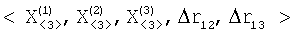 однозначно соответствует кривой второго порядка, являющейся линией положения ИРИ, и вместо этого вектора можно передать некоторое описание гиперболины. Минимальным набором данных, достаточным для описания кривой второго порядка в трехмерном пространстве, являются координаты трех точек, принадлежащих данной кривой. однозначно соответствует кривой второго порядка, являющейся линией положения ИРИ, и вместо этого вектора можно передать некоторое описание гиперболины. Минимальным набором данных, достаточным для описания кривой второго порядка в трехмерном пространстве, являются координаты трех точек, принадлежащих данной кривой.
Типовой формой гиперболины является гипербола или эллипс, а в отдельных случаях – парабола. Поэтому необходимо предусмотреть возможность передачи в векторе координат трех точек 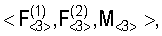 характеризующих гиперболину, информации о виде формы гиперболины и ее параметрах. характеризующих гиперболину, информации о виде формы гиперболины и ее параметрах.
Для эллипса и гиперболы целесообразно передавать координаты фокусов F1 и F2, а также точки М, принадлежащей гиперболине. При этом для эллипса – координаты точки М’, ортогональная проекция которой на прямую F1F2 принадлежит отрезку [F1O], где |F1O|=|F1F2|/2, а для гиперболы – координаты точки М”, ортогональная проекция которой на прямую F1F2 не принадлежит отрезку [F1F2]. Для параболы целесообразно передавать координаты фокуса F1, точки F2, являющейся проекцией точки F1 на директориальную плоскость, и точки М”’, ортогональная проекция которой на прямую F1F2 принадлежит отрезку [OF2], где |OF2|=|F1F2|/2 (фиг.4).
В силу сказанного, одиннадцатикомпонентный вектор 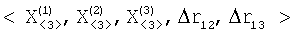 для уменьшения объема передаваемых данных без потери информации о местоположении ИРИ может быть заменен девятикомпонентным вектором для уменьшения объема передаваемых данных без потери информации о местоположении ИРИ может быть заменен девятикомпонентным вектором 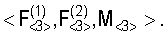
Таким образом, предлагаемый способ по сравнению с прототипом обеспечивает возможность снижения объема хранимых и передаваемых данных за счет замены одиннадцатикомпонентного вектора исходных данных эквивалентным ему по содержащейся информации девятитикомпонентным вектором.
Предложенный способ может быть применен как в системах наблюдения, так и в навигационных системах. Он позволяет снизить объем хранимых и передаваемых данных на 18%, что может быть использовано либо для повышения оперативности процесса передачи информации, либо для повышения качества связи за счет использования помехоустойчивого избыточного кодирования.
СПИСОК ЛИТЕРАТУРЫ
1. Многопозиционные радиотехнические системы / В.С.Кондратьев, А.Ф.Котов, Л.Н.Марков; Под ред. проф. В.В.Цветнова. – М.: Радио и связь, 1986. – 264 с.
2. Ярлыков М.С. Статистическая теория радионавигации. – М.: Радио и связь, 1985. – 344 с.
3. Сайбель А.Г. Разностно-дальномерный способ пеленгования источника радиоизлучения и реализующее его устройство. Патент РФ №2204145 от 10.05.2003.
4. Сетевые спутниковые радионавигационные системы / В.С.Шебшаевич, П.П.Дмитриев, Н.В.Иванцевич и др.; Под ред П.П.Дмитриева и В.С.Шебшаевича. – М.: Радио и связь, 1982. – 272 с, 1993. – 415 с.
5. Дулевич В.Е., Коростелев А.А., Мельник Ю.А. и др. Теоретические основы радиолокации / Под ред. В.Е.Дулевича. – М.: Сов. радио, 1964. – 732 с.
6. Теоретические основы радиолокации. Учебное пособие для вузов / Под ред. Я.Д.Ширмана. – М.: Сов. радио, 1970. – 560 с.
7. Финкельштейн М.И. Основы радиолокации. – М.: Сов. радио, 1973. – 496 с.
8. Белоцерковский Г.Б. Основы радиолокации и радиолокационные устройства. – М.: Сов. радио, 1975. – 336 с.
10. Способ определения местоположения передатчика путем измерения разности времен задержек. Пат. ГДР 274102.
11. Метод гиперболического определения места и устройство для его реализации. Пат. ГДР 229866.
16. Корн Г.А., Корн Т.М. Справочник по математике для научных работников и инженеров. Определения, теоремы, формулы. / Под общ. ред. И.Г.Арамановича. – М.: Наука, 1984. – 831 с.
Формула изобретения
Способ подготовки исходных данных разностно-дальномерной навигационной задачи, основанный на измерении двух разностей дальностей  r12 и r12 и  r13 от источника радиоизлучения до двух пар подвижных опорных точек {O1,O2} и {О1,О3}, координат r13 от источника радиоизлучения до двух пар подвижных опорных точек {O1,O2} и {О1,О3}, координат 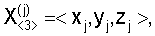 j=1, 2, 3 опорных точек Оj в момент времени измерения разностей дальностей, отличающийся тем, что преобразуют вектор измеренных значений j=1, 2, 3 опорных точек Оj в момент времени измерения разностей дальностей, отличающийся тем, что преобразуют вектор измеренных значений 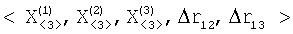 в вектор в вектор 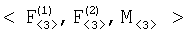 координат трех точек F1, F2 и М, принадлежащих гиперболине; вектор координат трех точек F1, F2 и М, принадлежащих гиперболине; вектор 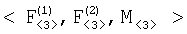 хранят и передают по каналам передачи информации в центр обработки информации для использования в качестве исходных данных при решении разностно-дальномерной навигационной задачи; при этом точки F1, и F2 определяют фокусы гиперболины, если она является гиперболой или эллипсом, или фокуса и его проекции на директрису, если она является параболой, а третья точка принадлежит гиперболине таким образом, что положение ее проекции на прямую F1F2 определяет вид кривой второго порядка. хранят и передают по каналам передачи информации в центр обработки информации для использования в качестве исходных данных при решении разностно-дальномерной навигационной задачи; при этом точки F1, и F2 определяют фокусы гиперболины, если она является гиперболой или эллипсом, или фокуса и его проекции на директрису, если она является параболой, а третья точка принадлежит гиперболине таким образом, что положение ее проекции на прямую F1F2 определяет вид кривой второго порядка.
РИСУНКИ
|