|
|
(21), (22) Заявка: 2005120470/09, 30.06.2005
(24) Дата начала отсчета срока действия патента:
30.06.2005
(43) Дата публикации заявки: 10.01.2007
(46) Опубликовано: 10.06.2007
(56) Список документов, цитированных в отчете о
поиске:
SU 369567 A1, 14.05.1973. SU 714399 A1, 08.02.1980. SU 888124 A1, 12.07.1981. SU 398950 A1, 01.01.1973.
Адрес для переписки:
355029, г.Ставрополь, пр-кт Кулакова, 2, СевКавГТУ
|
(72) Автор(ы):
Калмыков Игорь Анатольевич (RU),
Гахов Владислав Романович (RU),
Емарлукова Яна Вадимовна (RU)
(73) Патентообладатель(и):
Государственное образовательное учреждение высшего профессионального образования “Северо-Кавказский государственный технический университет” (RU)
|
(54) УСТРОЙСТВО ОБНАРУЖЕНИЯ И КОРРЕКЦИИ ОШИБОК В КОДАХ ПОЛИНОМИАЛЬНОЙ СИСТЕМЫ КЛАССОВ ВЫЧЕТОВ НА ОСНОВЕ НУЛЕВИЗАЦИИ
(57) Реферат:
Изобретение относится к вычислительной технике, в частности к модулярным нейрокомпьютерным средствам, и предназначено для выполнения операции поиска и коррекции ошибок в модулярных кодах полиномиальной системы классов вычетов (ПСКВ). Техническим результатом является повышение скорости обнаружения и коррекции ошибок в модулярных кодах ПСКВ. Указанный технический результат достигается за счет применения ПСКВ, в которой в качестве основания системы используется минимальные многочлены pi(z), i=1, 2, …, 7, определенные в расширенных полях Галуа GF(25) и нейросетевых технологий, а также параллельного применения модифицированных констант нулевизации, определяемых в данной ПСКВ. 2 ил., 7 табл.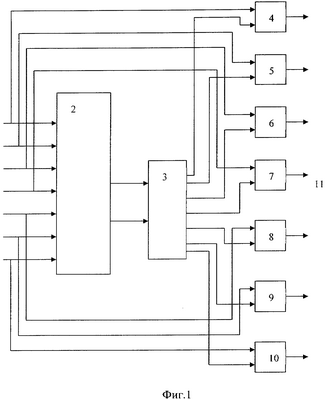
Изобретение относится к вычислительной технике, в частности к модулярным нейрокомпьютерным средствам, и предназначено для выполнения операции поиска и коррекции ошибок в модулярных кодах полиноминальной системы классов вычетов (ПСКВ).
Целью изобретения является повышение, скорости определения местоположения и глубины ошибок в модулярном коде ПСКВ для коррекции результата на основе способа нулевизации. Цель достигается за счет перехода от последовательного характера выполнения операции нулевизации к параллельному вычитанию констант нулевизации, а также применению нейросетевого базиса и выполнению операций в полиномиальной системе классов вычетов расширенного поля Галуа GF(2 ). ).
Техническим результатом, достигаемым при осуществлении заявленного изобретения, является повышение скорости обнаружения и коррекции ошибок в модулярных кодах ПСКВ.
Указанный технический результат достигается за счет применения полиномиальной системы классов вычетов (ПСКВ), в которой в качестве основания системы используются минимальные многочлены pi(z), i=1, 2, …, k+r, определенные в расширенных полях Галуа GF(2 ), и нейросетевых технологий, а также параллельного применения модифицированных констант нулевизации, определяемых в данной ПСКВ. ), и нейросетевых технологий, а также параллельного применения модифицированных констант нулевизации, определяемых в данной ПСКВ.
Если в качестве оснований новой алгебраической системы выбрать минимальные многочлены pi(z) поля GF(p ), то любой полином A(z), удовлетворяющий условию ), то любой полином A(z), удовлетворяющий условию
A(z) Pпол, Pпол,
где 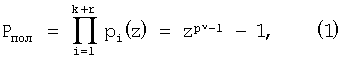
можно представить в виде n-мерного вектора
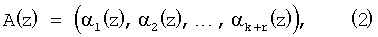
где  , i=1, 2, …, k+r. , i=1, 2, …, k+r.
Так как сравнения по одному и тому же модулю можно почленно складывать, вычитать и умножать, то для суммы, разности и произведения двух полиномов A(z) и B(z), имеющих соответственно модулярные коды ( 1(z), 1(z), 2(z),…, 2(z),…, k+r(z)) и ( k+r(z)) и ( 1(z), 1(z), 2(z),…, 2(z),…, k+r(z)) справедливы соотношения: k+r(z)) справедливы соотношения:
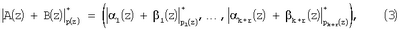
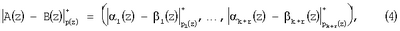
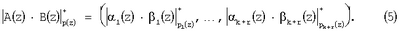
Таким образом, выполнение операций над операндами в расширенном поле Галуа GF(р ) производятся независимо по каждому из модулей pi(z), что указывает на параллелизм данной алгебраической системы. ) производятся независимо по каждому из модулей pi(z), что указывает на параллелизм данной алгебраической системы.
Кроме того, особенность ПСКВ состоит еще и в том, что независимость обработки информации по основаниям ПСКВ позволяет не только повысить скорость и точность обработки, но также и обеспечить обнаружение и коррекцию ошибок в процессе функционирования вычислительного устройства класса вычетов. Если на диапазон возможного изменения кодируемого множества полиномов наложить ограничения, то есть выбрать k из n оснований ПСКВ (kполн(z) расширенного поля Галуа GF(p ) на два непересекающихся подмножества.),> ) на два непересекающихся подмножества.),>
Первое подмножество называется рабочим диапазоном и определяется выражением
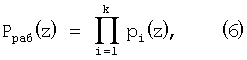
Многочлен A(z) с коэффициентами из поля GF(р) будет считаться разрешенным в том и только том случае, если он является элементом нулевого интервала полного диапазона Pполн(z), то есть принадлежит рабочему диапазону A(z) Pраб(z). Pраб(z).
Второе подмножество GF(р ), определяемое произведением r=n-k контрольных оснований ), определяемое произведением r=n-k контрольных оснований
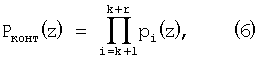
задает совокупность запрещенных комбинаций. Если A(z) является элементом второго подмножества, то считается, что данная комбинация содержит ошибку. Таким образом, местоположение полинома A(z) относительно двух данных подмножеств позволяет однозначно определить, является ли кодовая комбинация A(z)=( 1(z), 1(z), 2(z),…, 2(z),…, k+r(z)) разрешенной, или содержит ошибочные символы. k+r(z)) разрешенной, или содержит ошибочные символы.
Для определения местоположения A(z)=( 1(z), 1(z),  2(z),…, 2(z),…,  k+r(z)) в работе (Акушский И.Я., Юдицкий Д.И. Машинная арифметика в остаточных классах. – М.: Советское радио, 1968. – 439 с. (стр.193-194)) предложено использовать способ нулевизации, заключающийся в переходе от исходного полинома к полиному вида k+r(z)) в работе (Акушский И.Я., Юдицкий Д.И. Машинная арифметика в остаточных классах. – М.: Советское радио, 1968. – 439 с. (стр.193-194)) предложено использовать способ нулевизации, заключающийся в переходе от исходного полинома к полиному вида
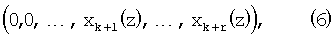
при помощи последовательных преобразований, при которых не имеет место ни один выход за пределы рабочего диапазона системы.
Согласно этому способу нулевизация заключается в последовательном вычитании из исходного полинома, представленного в модулярном коде, некоторых минимальных полиномов – констант нулевизации таких, что полином A(z) последовательно преобразуется в полином вида
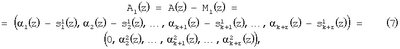
где 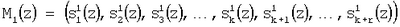 – константа нулевизации по первому основанию p1(z). – константа нулевизации по первому основанию p1(z).
Затем из полученного результата вычитается следующая константа нулевизации для получения полинома
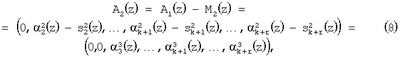
где 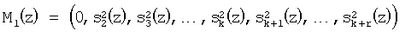 по второму основанию p2(z), и так далее. Продолжая данный процесс в течение k итераций, получается по второму основанию p2(z), и так далее. Продолжая данный процесс в течение k итераций, получается
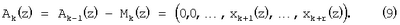
Применение способа нулевизации позволяет последовательно получать наименьший полином, кратный сначала p1(z), затем полином – кратный p1(z)p2(z), и в конечном итоге – кратный рабочему диапазону 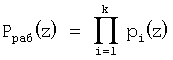 . .
Если в результате последовательного выполнения процедуры нулевизации будет получен нулевой результат, т.е.
xk+1(z)=0, xk+2(z)=0,…,xk+r(z)=0,
то это свидетельствует, что исходная комбинация A(z), представленная в модулярном коде, не содержит ошибок. В противном случае – модулярный код A(z) – содержит ошибки.
Основным недостатком известного метода нулевизации является последовательный характер вычислительного процесса. Это обусловлено прежде всего тем, что константы нулевизации представляют собой наименьшие возможные числа вида
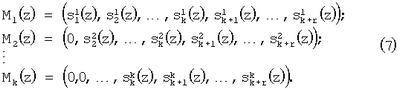
где 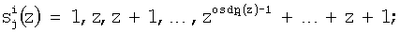  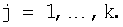
Повысить скорость выполнения-процедуры нулевизации можно за счет модификации констант нулевизации Mi(z). Оставляя неизменным условие невыхода константы нулевизации Mi(z) за пределы рабочего диапазона 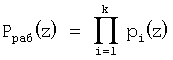 , возьмем в качестве последних значения произведение остатков рабочих оснований на величину ортогональных базисов безызбыточной системы оснований , возьмем в качестве последних значения произведение остатков рабочих оснований на величину ортогональных базисов безызбыточной системы оснований
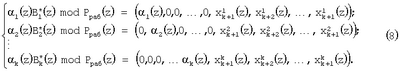
где 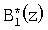 – ортогональный базис, безызбыточной системы оснований; i=1, 2, …, k. – ортогональный базис, безызбыточной системы оснований; i=1, 2, …, k.
Тогда если положить условие, что A(z) Pраб(z), где Pраб(z), где 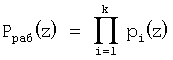 , то полином A(z)=( , то полином A(z)=( 1(z), 1(z), 2(z)…, 2(z)…, k(z)) согласно китайской теореме об остатках (КТО) можно представить в виде k(z)) согласно китайской теореме об остатках (КТО) можно представить в виде
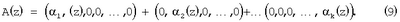
Каждое слагаемое выражения (9) представляет собой
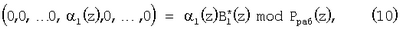
Подставим выражения (8) в равенство (10). Получаем
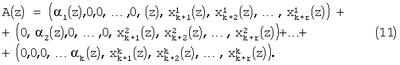
Следовательно, значения остатков по контрольным основаниям будут определяться
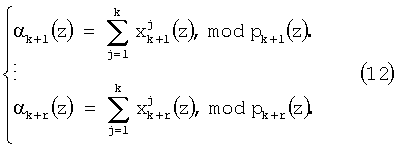
Значит, разность полинома A(z) и модифицированных констант нулевизации Mi(z), i=1, 2, …, k, псевдоортогональных форм, полученных согласно (4.5), задает величину нормированного следа полинома
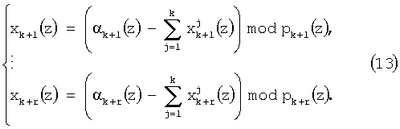
Исходя из условия, что модифицированные константы нулевизации Mi(z) представляют собой ортогональные базисы безызбыточной системы оснований ПСКВ, то операция нулевизации (13) может быть реализована параллельно.
Для уменьшения объема хранимых значений констант нулевизации Mi(z), i=1, 2, …, k, представим остатком числа  i(z) в виде i(z) в виде
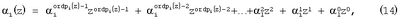
где 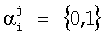 элементы поля GF(2); j=0, 1, …, ordpi(z)-1. элементы поля GF(2); j=0, 1, …, ordpi(z)-1.
Тогда справедливо
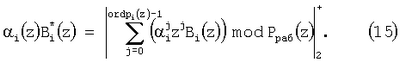
Таким образом, вместо хранения 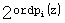 констант нулевизации Mi(z) достаточно определить ordpi(z) констант. констант нулевизации Mi(z) достаточно определить ordpi(z) констант.
Рассмотрим ПСКВ, определяемую в поле GF(25). В таблице 1 помещены значения рабочих и контрольных оснований ПСКВ, а также динамический диапазон для расширенного поля Галуа.
| Таблица 1 |
| Основания и динамический диапазон поля GF(25) |
| Основания ПСКВ |
Рабочий диапазон |
| Рабочие |
Контрольные |
ПСКВ |
| p1(z)=z+1 |
p6(z)=z5+z2+1 |
z21+z19+z16+z13+ |
| p2(z)=z5+z3+1 |
p7(z)=z5+z3+z2+z+1 |
+z11+z9+z8+z6+ |
| p3(z)=z5+z4+z2+z+1 |
|
+z3+z2+z+1 |
| p4(z)=z5+z4+z3+z+1 |
|
|
| p5=z5+z4+z3+z2+1 |
|
|
Ортогональные базисы безызбыточной системы оснований ПСКВ p1(z), p2(z), р3(z), p4(z), p5(z) принимают следующие значения
B1 *(z)=z20+z19+z15+z14+z13+z10+z9+z7+z6+z2+1;
B2 *(z)=z16+z8+z4+z2+z+1;
B3 *(z)=z20+z18+z16+z15+z14+z13+z12+z11+z10+z6+z3+z;
B4 *(z)=z19+z18+z16+z15+z14+z13+z8+z7+z6+z5+z4+z;
Bl *(z)=z16+z15+z14+z13+z12+z11+z9+z6+z5+z3+z+1.
Определим все значения произведений степеней zj на ортогональные базисы Bi *(z), учитывая невозможность выхода за пределы рабочего диапазона Pраб(z)=z21+z19+z16+z13+z11+z9+z8+z6+z3+z2+z+1. Полученные значения модифицированных констант нулевизации представлены в таблице 2.
| Таблица 2 |
| Константы нулевизации для поля GF(25) |
| |
 1(z) 1(z) |
 2(z) 2(z) |
 3(z) 3(z) |
 4(z) 4(z) |
 5(z) 5(z) |
 6(z) 6(z) |
 7(z) 7(z) |
| z0B1 *(z) |
1 |
0 |
0 |
0 |
0 |
z2 |
z |
| z0B2 *(z) |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
| z1B2 *(z) |
0 |
z |
0 |
0 |
0 |
z |
z |
| z2B2 *(z) |
0 |
z2 |
0 |
0 |
0 |
z2 |
z2 |
| z3B2 *(z) |
0 |
z3 |
0 |
0 |
0 |
z3 |
z3 |
| z4B2 *(z) |
0 |
z4 |
0 |
0 |
0 |
z4 |
z4 |
| z0B3 *(z) |
0 |
0 |
1 |
0 |
0 |
z4+z |
z4+1 |
| z1B3 *(z} |
0 |
0 |
z |
0 |
0 |
z3+z2+1 |
z3+z+1 |
| z2B3 *(z) |
0 |
0 |
z2 |
0 |
0 |
z4+z3+z |
z4+z2+z |
| z3B3 *(z) |
0 |
0 |
z3 |
0 |
0 |
z4+1 |
z+1 |
| z4B3 *(z) |
0 |
0 |
z4 |
0 |
0 |
z2+z+1 |
z2+z |
| z0B4 *(z) |
0 |
0 |
0 |
1 |
0 |
z2 |
z+1 |
| z1B4 *(z) |
0 |
0 |
0 |
z |
0 |
z3 |
z2+z |
| z2B4 *(z) |
0 |
0 |
0 |
z2 |
0 |
z4+z3+z2 |
z3+z |
| z3B4 *(z) |
0 |
0 |
0 |
z3 |
0 |
z4+z |
z4+z2 |
| z4B4 *(z) |
0 |
0 |
0 |
z4 |
0 |
z3+z+1 |
z3+z2+1 |
| z0B5 *(z) |
0 |
0 |
0 |
0 |
1 |
z4+z |
z4 |
| z1B5 *(z) |
0 |
0 |
0 |
0 |
z |
1 |
z3+z2+z+1 |
| z2B5 *(z) |
0 |
0 |
0 |
0 |
z2 |
z |
z4+z3+z2+z |
| z3B5 *(z) |
0 |
0 |
0 |
0 |
z3 |
z2 |
z4+z+1 |
| z4B5 *(z) |
0 |
0 |
0 |
0 |
z4 |
z3 |
z3+1 |
Если в упорядоченной избыточной ПСКВ расширенного поля Галуа GF(p ) для которой справедливо ordp1(z) ) для которой справедливо ordp1(z) ordp2(z) ordp2(z) … … ordpk(z) для двух контрольных оснований pk+1(z) и pk+2(z) имеет место соотношение ordpk(z) для двух контрольных оснований pk+1(z) и pk+2(z) имеет место соотношение
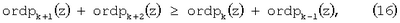
то они определяют местоположение и величину ошибки по любому основанию.
Рассмотрим пример. Пусть в поле GF(25), в котором определены рабочие и контрольные основания согласно таблице 1, задан – полином A(z)=z6+z5+z4+1, Данный полином принадлежит Pраб(z). Представим его в модулярном коде
A(z)=z6+z5+z4+1=(0,z3+z,z4+z3+z2+z+1,z2+z+1,z3+z+1,z4+z3+z2+z,0).
Проведем последовательно процедуру нулевизации. На первом этапе путем вычитания по модулю 2 получаем
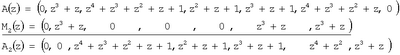
Значение М2(z) получено согласно выражению (15) путем суммирования значений
M2(z)=z3B2 *(z)+zB2 *(z)=(0, z3, 0, 0, 0, z3, z3)+(0, z, 0, 0, 0, z, z)=(0, z3+z, 0, 0, 0, z3+z, z3+z).
На втором этапе нулевизации имеем
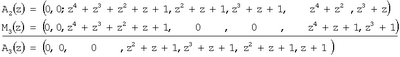
На третьем этапе нулевизации получаем
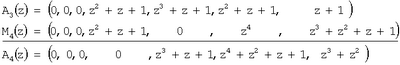
На четвертом этапе нулевизации имеем
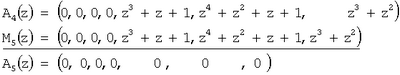
Таким образом, полином A(z) не содержит ошибки.
| Таблица 3 |
| Зависимость местоположения и глубины ошибки от результатов выполнения процедуры нулевизации |
| Результат нулевизации |
Ошибка в модулярном коде |
| x6(z) |
x7(z) |
глубина |
основание |
| z2 |
z |
1 |
p1(z)=z+1 |
| 1 |
1 |
1 |
p2(z)=z5+z3+1 |
| z |
z |
z |
| z2 |
z2 |
z2 |
| z3 |
z3 |
z3 |
| z4 |
z4 |
z4 |
| z4+z |
z4+1 |
1 |
p3(z)=z5+z4+z2+z+1 |
| z3+z2+1 |
z3+z+1 |
z |
| z4+z3+z |
z4+z2+z |
z2 |
| z4+1 |
z+1 |
z3 |
| z2+z+1 |
z2+z |
z4 |
| z2 |
z+1 |
1 |
p4(z)=z5+z4+z3+z+1 |
| z3 |
z2+z |
z |
| z4+z3+z2 |
z3+z |
z2 |
| z4+1 |
z4+z2 |
z3 |
| z3+z+1 |
z3+z2+1 |
z4 |
| z4+z |
z4 |
1 |
p5(z)=z5+z4+z3+z2+1 |
| 1 |
z3+z2+z+1 |
z |
| z |
z4+z3+z2+z |
z2 |
| z2 |
z4+z+1 |
z3 |
| z3 |
z3+1 |
z4 |
| 1 |
0 |
1 |
p6(z)=z5+z3+1 |
| z |
0 |
z |
| z2 |
0 |
z2 |
| z3 |
0 |
z3 |
| z4 |
0 |
z4 |
| 0 |
1 |
1 |
p7(z)=z5+z3+z2+z+1 |
| 0 |
z |
z |
| 0 |
z2 |
z2 |
| 0 |
z3 |
z3 |
| 0 |
z4 |
z4 |
Допустим ошибка произошла по первому основанию. Тогда имеем
A*(z)=(1, z3+z, z4+z3+z2+z+1, z2+z+1, z3+z+1,z4+z3+z2+z, 0).
Проведем последовательно процедуру нулевизации. На первом этапе путем вычитания по модулю 2 получаем
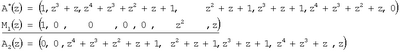
На втором этапе нулевизации имеем
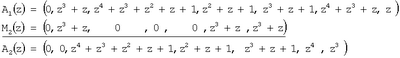
На третьем этапе нулевизации получаем
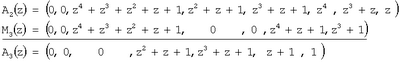
На четвертом этапе нулевизации имеем
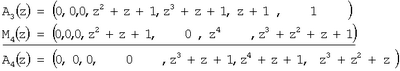
На четвертом этапе нулевизации имеем
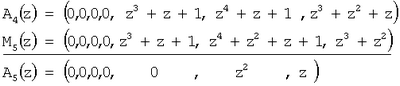
В результате проведения нулевизации был получен ненулевой результат, который свидетельствует о наличии ошибки в модулярном коде.
В зависимости от величины синдрома ошибки осуществляется коррекция
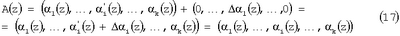
где (0,…,  i(z),…,0) – вектор ошибки модулярного кода; i(z),…,0) – вектор ошибки модулярного кода;   i(z) – глубина ошибки по i-му модулю; i(z) – глубина ошибки по i-му модулю; 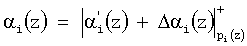 . .
Согласно таблице 3, где приведена зависимость местоположения и глубины ошибки от результатов выполнения процедуры нулевизации, для полученного результата x6(z)=z2, x7(z)=z имеем, что ошибка произошла по первому основанию и глубина равна 1. Тогда исходный полином имеет вид
A*(z)+(1, 0, 0, 0, 0, 0, 0)=(0, z3+z, z4+z3+z2+z+1, z2+z+1, z3+z+1, z4+z3+z2+z, 0).
Структура устройства обнаружения и коррекции ошибок в кодах полиномиальной системы классов вычетов на основе нулевизации представлена на фигуре 1.
Она включает: вход устройства 1, блок нулевизации 2, блок памяти 3, сумматоры 4, 5, 6, 7, 8, 9, 10, выход устройства 11.
Работа устройства осуществляется следующим образом.
На вход 1 устройства обнаружения и коррекции ошибок в кодах полиномиальной системы классов вычетов на основе нулевизации подается контролируемое число, представленное в полиномиальной форме
A(z)=( 1(z), 1(z),  2(z), 2(z),  3(z), 3(z),  4(z), 4(z),  5(z), 5(z),  6(z), 6(z),  7(z)). 7(z)).
где  i(z) – остаток полинома A(z) по модулю pi(z); p1(z), р2(z), p3(z), p4(z), p5(z) – рабочие основания системы ПСКВ поля GF(25); p6(z), p7(z) – контрольные основания. Вход устройства соединен с входами блока нулевизации 2. С выхода блока нулевизации вычисленные значения x6(z), x7(z) подаются на входы блока памяти 3 и выбирают оттуда соответствующую константу ошибки (0,…, i(z) – остаток полинома A(z) по модулю pi(z); p1(z), р2(z), p3(z), p4(z), p5(z) – рабочие основания системы ПСКВ поля GF(25); p6(z), p7(z) – контрольные основания. Вход устройства соединен с входами блока нулевизации 2. С выхода блока нулевизации вычисленные значения x6(z), x7(z) подаются на входы блока памяти 3 и выбирают оттуда соответствующую константу ошибки (0,…,  i(z),…,0), i=1, 2, 3, 4, 5, 6, 7. Эта константа ошибки поступает на вторые входы корректирующих сумматоров 4, 5, 6, 7, 8, 9, 10 соответственно по основаниям p1(z), р2(z), р3(z), p4(z), p5(z), p6(z), p7(z), где суммируется с поступившими на первые входы значениями i(z),…,0), i=1, 2, 3, 4, 5, 6, 7. Эта константа ошибки поступает на вторые входы корректирующих сумматоров 4, 5, 6, 7, 8, 9, 10 соответственно по основаниям p1(z), р2(z), р3(z), p4(z), p5(z), p6(z), p7(z), где суммируется с поступившими на первые входы значениями  1(z), 1(z),  2(z), 2(z),  3(z), 3(z),  4(z), 4(z),  5(z), 5(z),  6(z), 6(z),  7(z), подаваемые со входа устройства 1. Исправленное значение A(z) согласно равенству (17) с выхода корректирующих сумматоров 4-10 подается на выход 11 устройства. 7(z), подаваемые со входа устройства 1. Исправленное значение A(z) согласно равенству (17) с выхода корректирующих сумматоров 4-10 подается на выход 11 устройства.
Блок нулевизации представлен на фиг.2.
Она состоит из: первый слой нейронов 12-42, второй слой нейронов 43-52.
Блок нулевизации представляет собой двухслойную нейронную сеть. Первый слой содержит 31 нейрон. На вход нейронов 12 в двоичном коде поступает остаток  1(z) по основанию p1(z)=z+1. На вход нейронов 13-17 поступает остаток 1(z) по основанию p1(z)=z+1. На вход нейронов 13-17 поступает остаток  2(z) по основанию p2(z)=z5+z3+1, причем старший разряд подается на 13 нейрон, а младший – 17 нейрон. На вход нейронов 18-22 поступает остаток 2(z) по основанию p2(z)=z5+z3+1, причем старший разряд подается на 13 нейрон, а младший – 17 нейрон. На вход нейронов 18-22 поступает остаток  3(z) по основанию p3(z)=z5+z4+z2+z+1, причем старший разряд подается на 18 нейрон, а младший – 22 нейрон. На вход нейронов 23-27 поступает остаток 3(z) по основанию p3(z)=z5+z4+z2+z+1, причем старший разряд подается на 18 нейрон, а младший – 22 нейрон. На вход нейронов 23-27 поступает остаток  4(z) по основанию p4(z)=z5+z4+z3+z+1, причем старший разряд подается на 23 нейрон, а младший – 27 нейрон. На вход нейронов 28-32 поступает остаток 4(z) по основанию p4(z)=z5+z4+z3+z+1, причем старший разряд подается на 23 нейрон, а младший – 27 нейрон. На вход нейронов 28-32 поступает остаток  5(z) по основанию p5(z)=z5+z4+z3+z2+1, причем старший разряд подается на 28 нейрон, а младший – 32 нейрон. На нейроны 33-37 поступает двоичный код 5(z) по основанию p5(z)=z5+z4+z3+z2+1, причем старший разряд подается на 28 нейрон, а младший – 32 нейрон. На нейроны 33-37 поступает двоичный код  6(z) по первому контрольному модулю p6(z)=z5+z2+1, причем старший разряд подается на 33 нейрон, а младший – на 37 нейрон. На нейроны 38-42 в двоичном коде поступает в двоичном коде 6(z) по первому контрольному модулю p6(z)=z5+z2+1, причем старший разряд подается на 33 нейрон, а младший – на 37 нейрон. На нейроны 38-42 в двоичном коде поступает в двоичном коде  7(z) по второму контрольному модулю p7(z)=z5+z3+z2+z+1, причем старший разряд подается на 38 нейрон, а младший – на 42 нейрон. Второй слой нейронной сети содержит 10 нейронов, выполняющих базовую операцию суммирования по модулю два согласно выражению (13), причем первые пять нейронов 43-47 определяют значение x6(z), остальные нейроны 48-52 определяют значение x7(z). Входы нейрона 43 второго слоя соединены с выходами нейронов 13, 19, 20, 22, 24, 25, 32, 33 нейронов первого слоя. Входы нейрона 44 второго слоя соединены с выходами нейронов 14, 20, 21, 23, 25, 26, 28, 34 нейронов первого слоя. Входы нейрона 45 второго слоя соединены с выходами нейронов 12, 15, 18, 21, 25, 27, 29, 35 нейронов первого слоя. Входы нейрона 46 второго слоя соединены с выходами нейронов 16, 18, 20, 22, 23, 30, 32, 36 нейронов первого слоя. Входы нейрона 47 второго слоя соединены с выходами нейронов 17, 18, 19, 21, 23, 24, 31, 37 нейронов первого слоя. Входы нейрона 48 второго слоя соединены с выходами нейронов 13, 20, 22, 24, 29, 30, 31, 38 нейронов первого слоя. Входы нейрона 49 второго слоя соединены с выходами нейронов 14, 21, 23, 25, 28, 30, 31, 39 нейронов первого слоя. Входы нейрона 50 второго слоя соединен с выходами нейронов 15, 18, 20, 23, 26, 30, 31, 40 нейронов первого слоя. Входы нейрона 51 второго слоя соединен с выходами нейронов 12, 16, 18, 19, 20, 21, 24, 25, 26, 27, 29, 30, 31, 41 нейронов первого слоя. Входы нейрона 52 второго слоя соединен с выходами нейронов 17, 19, 21, 22, 23, 27, 28, 29, 31, 42 нейронов первого слоя. Старшие значения результатов нулевизации по контрольным основаниям x6(z) и x7(z) соответственно вычисляются в нейронах 43 и 48. 7(z) по второму контрольному модулю p7(z)=z5+z3+z2+z+1, причем старший разряд подается на 38 нейрон, а младший – на 42 нейрон. Второй слой нейронной сети содержит 10 нейронов, выполняющих базовую операцию суммирования по модулю два согласно выражению (13), причем первые пять нейронов 43-47 определяют значение x6(z), остальные нейроны 48-52 определяют значение x7(z). Входы нейрона 43 второго слоя соединены с выходами нейронов 13, 19, 20, 22, 24, 25, 32, 33 нейронов первого слоя. Входы нейрона 44 второго слоя соединены с выходами нейронов 14, 20, 21, 23, 25, 26, 28, 34 нейронов первого слоя. Входы нейрона 45 второго слоя соединены с выходами нейронов 12, 15, 18, 21, 25, 27, 29, 35 нейронов первого слоя. Входы нейрона 46 второго слоя соединены с выходами нейронов 16, 18, 20, 22, 23, 30, 32, 36 нейронов первого слоя. Входы нейрона 47 второго слоя соединены с выходами нейронов 17, 18, 19, 21, 23, 24, 31, 37 нейронов первого слоя. Входы нейрона 48 второго слоя соединены с выходами нейронов 13, 20, 22, 24, 29, 30, 31, 38 нейронов первого слоя. Входы нейрона 49 второго слоя соединены с выходами нейронов 14, 21, 23, 25, 28, 30, 31, 39 нейронов первого слоя. Входы нейрона 50 второго слоя соединен с выходами нейронов 15, 18, 20, 23, 26, 30, 31, 40 нейронов первого слоя. Входы нейрона 51 второго слоя соединен с выходами нейронов 12, 16, 18, 19, 20, 21, 24, 25, 26, 27, 29, 30, 31, 41 нейронов первого слоя. Входы нейрона 52 второго слоя соединен с выходами нейронов 17, 19, 21, 22, 23, 27, 28, 29, 31, 42 нейронов первого слоя. Старшие значения результатов нулевизации по контрольным основаниям x6(z) и x7(z) соответственно вычисляются в нейронах 43 и 48.
Рассмотрим процесс работы блока нулевизации на примерах. Пусть на вход устройство обнаружения и коррекции ошибок в кодах полиномиальной системы классов вычетов на основе нулевизации был подан модулярный код A(z)=(0, z3+z, z4+z3+z2+z+1, z2+z-1, z4+z3+z2+1, 0). Данный код поступает на входы нейронов первого слоя блока нулевизации. Сигналы на выходе нейронов первого слоя представлены в таблице 4.
Сигналы с выходов нейронов первого слоя поступают на соответствующие входы нейронов второго слоя. В таблице 5 представлены значения сигналов на входе и на выходе нейронов второго слоя. Символ «-» соответствует отсутствию связи между нейронами второго и первого слоя. Полученный нулевой результат свидетельствует о том, что данная комбинация не содержит ошибки.
Допустим, что ошибка произошла по первому основанию. Тогда модульная комбинация имеет вид
A*(z)=(1, z3+z, z4+z3+z2+z+1, z2+z+1, z3+z+1, z4+z3+z2+z, 0)
Данный код поступает на входы нейронов первого слоя блока нулевизации. Сигналы на выходе нейронов первого слоя представлены в таблице 6.
Сигналы с выходов нейронов первого слоя поступают на соответствующие входы нейронов второго слоя. В таблице 7 представлены значения сигналов на входе и на выходе нейронов второго слоя.
В результате выполнения процедуры, параллельной нулевизации, был получен результат, отличный от нулевого, т.е. x6(z)=z2, x7(z)=z. Следовательно, модульная комбинация, поданная на вход устройства, содержит ошибку.
Согласно таблице 3, где приведена зависимость местоположения и глубины ошибки от результатов выполнения процедуры нулевизации, для полученного результата x6(z)=z2, x7(z)=z имеем, что ошибка произошла по первому основанию и глубина равна 1.
| Таблица 4 |
| Сигналы на выходе нейронов первого слоя |
| Нейрон |
Сигнал |
| 12 |
0 |
| 13 |
0 |
| 14 |
1 |
| 15 |
0 |
| 16 |
1 |
| 17 |
0 |
| 18 |
1 |
| 19 |
1 |
| 20 |
1 |
| 21 |
1 |
| 22 |
1 |
| 23 |
0 |
| 24 |
0 |
| 25 |
1 |
| 26 |
1 |
| 27 |
1 |
| 28 |
0 |
| 29 |
1 |
| 30 |
0 |
| 31 |
1 |
| 32 |
1 |
| 33 |
1 |
| 34 |
1 |
| 35 |
1 |
| 36 |
1 |
| 37 |
0 |
| 38 |
0 |
| 39 |
0 |
| 40 |
0 |
| 41 |
0 |
| 42 |
0 |
| Таблица 5 |
| Сигналы на выходе нейронов второго слоя |
| 52 |
51 |
50 |
49 |
48 |
47 |
46 |
45 |
44 |
43 |
|
| – |
0 |
– |
– |
– |
– |
– |
0 |
– |
– |
12 |
| – |
– |
– |
– |
0 |
– |
– |
– |
– |
0 |
13 |
| – |
– |
– |
1 |
– |
|
– |
– |
1 |
– |
14 |
| – |
– |
0 |
– |
– |
– |
– |
0 |
– |
– |
15 |
| – |
1 |
– |
– |
– |
– |
1 |
– |
– |
– |
16 |
| 0 |
– |
– |
– |
– |
0 |
– |
– |
– |
– |
17 |
| – |
1 |
1 |
– |
– |
1 |
1 |
1 |
– |
|
18 |
| 1 |
1 |
– |
– |
– |
1 |
– |
– |
– |
1 |
19 |
| – |
1 |
1 |
– |
1 |
– |
1 |
– |
1 |
1 |
20 |
| 1 |
1 |
– |
1 |
– |
1 |
– |
1 |
1 |
– |
21 |
| 1 |
– |
– |
– |
1 |
– |
1 |
– |
– |
1 |
22 |
| 0 |
– |
0 |
0 |
– |
0 |
0 |
– |
0 |
– |
23 |
| – |
0 |
– |
– |
0 |
0 |
– |
– |
– |
0 |
24 |
| – |
1 |
– |
1 |
– |
– |
– |
1 |
1 |
1 |
25 |
| – |
1 |
1 |
– |
– |
– |
– |
– |
1 |
– |
26 |
| 1 |
1 |
– |
– |
– |
– |
– |
1 |
– |
– |
27 |
| 0 |
– |
– |
0 |
– |
– |
– |
– |
0 |
– |
28 |
| 1 |
1 |
– |
– |
1 |
– |
– |
1 |
– |
– |
29 |
| – |
0 |
0 |
0 |
0 |
– |
0 |
– |
– |
– |
30 |
| 1 |
1 |
1 |
1 |
1 |
1 |
– |
– |
– |
– |
31 |
| – |
– |
– |
– |
– |
– |
1 |
– |
– |
1 |
32 |
| – |
– |
– |
– |
– |
– |
– |
– |
– |
1 |
33 |
| – |
– |
– |
– |
– |
– |
– |
– |
1 |
– |
34 |
| – |
– |
– |
– |
– |
– |
– |
1 |
– |
– |
35 |
| – |
– |
– |
– |
– |
– |
1 |
– |
– |
– |
36 |
| – |
– |
– |
– |
– |
0 |
– |
– |
– |
– |
37 |
| – |
– |
– |
– |
0 |
– |
– |
– |
– |
— |
38 |
| – |
– |
– |
0 |
– |
– |
– |
– |
– |
– |
39 |
| – |
– |
0 |
– |
– |
– |
– |
– |
– |
– |
40 |
| – |
0 |
– |
– |
– |
– |
– |
– |
– |
– |
41 |
| 0 |
– |
– |
– |
– |
– |
– |
– |
– |
– |
42 |
| 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
Выход |
| Таблица 6 |
| Сигналы на выходе нейронов первого слоя (при возникновении ошибки) |
| Нейрон |
Сигнал |
| 12 |
1 |
| 13 |
0 |
| 14 |
1 |
| 15 |
0 |
| 16 |
1 |
| 17 |
0 |
| 18 |
1 |
| 19 |
1 |
| 20 |
1 |
| 21 |
1 |
| 22 |
1 |
| 23 |
0 |
| 24 |
0 |
| 25 |
1 |
| 26 |
1 |
| 27 |
1 |
| 28 |
0 |
| 29 |
1 |
| 30 |
0 |
| 31 |
1 |
| 32 |
1 |
| 33 |
1 |
| 34 |
1 |
| 35 |
1 |
| 36 |
1 |
| 37 |
0 |
| 38 |
0 |
| 39 |
0 |
| 40 |
0 |
| 41 |
0 |
| 42 |
0 |
| Таблица 7 |
| Сигналы на выходе нейронов второго слоя (при возникновении ошибки) |
| 52 |
51 |
50 |
49 |
48 |
47 |
46 |
45 |
44 |
43 |
|
| – |
1 |
– |
– |
– |
– |
– |
1 |
– |
– |
12 |
| – |
– |
– |
– |
0 |
|
– |
– |
– |
0 |
13 |
| – |
– |
– |
1 |
– |
– |
– |
– |
1 |
– |
14 |
| – |
– |
0 |
– |
– |
– |
– |
0 |
– |
– |
15 |
| – |
1 |
– |
– |
– |
– |
1 |
– |
– |
– |
16 |
| 0 |
– |
– |
– |
– |
0 |
– |
– |
– |
|
17 |
| – |
1 |
1 |
– |
– |
1 |
1 |
1 |
– |
– |
18 |
| 1 |
1 |
– |
– |
– |
1 |
– |
– |
– |
1 |
19 |
| – |
1 |
1 |
– |
1 |
– |
1 |
– |
1 |
1 |
20 |
| 1 |
1 |
– |
1 |
– |
1 |
– |
1 |
1 |
– |
21 |
| 1 |
– |
– |
1 |
– |
– |
1 |
– |
– |
1 |
22 |
| 0 |
– |
0 |
0 |
– |
0 |
0 |
– |
0 |
– |
23 |
| – |
0 |
– |
– |
0 |
0 |
– |
– |
– |
0 |
24 |
| – |
1 |
– |
1 |
– |
– |
– |
1 |
1 |
1 |
25 |
| – |
1 |
1 |
– |
– |
– |
– |
– |
1 |
– |
26 |
| 1 |
1 |
– |
– |
– |
– |
– |
1 |
– |
– |
27 |
| 0 |
– |
– |
0 |
– |
– |
– |
– |
0 |
– |
28 |
| 1 |
1 |
– |
– |
1 |
– |
– |
1 |
– |
– |
29 |
| – |
0 |
0 |
0 |
0 |
– |
0 |
– |
– |
– |
30 |
| 1 |
1 |
1 |
1 |
1 |
1 |
– |
– |
– |
– |
31 |
| – |
– |
– |
– |
– |
– |
1 |
– |
– |
1 |
32 |
| – |
– |
– |
– |
– |
– |
– |
– |
– |
1 |
33 |
| – |
– |
– |
– |
– |
– |
– |
– |
1 |
– |
34 |
| – |
– |
– |
– |
– |
– |
– |
1 |
– |
– |
35 |
| – |
– |
– |
– |
– |
– |
1 |
– |
– |
– |
36 |
| – |
– |
– |
– |
– |
0 |
– |
– |
– |
|
37 |
| – |
– |
– |
– |
0 |
– |
– |
– |
– |
– |
38 |
| – |
– |
– |
0 |
– |
– |
– |
– |
– |
– |
39 |
| – |
– |
0 |
– |
– |
– |
– |
– |
– |
– |
40 |
| – |
0 |
– |
– |
– |
– |
– |
– |
– |
– |
41 |
| 0 |
– |
– |
– |
– |
– |
– |
– |
– |
– |
42 |
| 0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
Выход |
Формула изобретения
Устройство обнаружения и коррекции ошибок на основе нулевизации в кодах полиномиальной системы классов вычетов (ПСКВ) в исходном полиноме A(z)=( 1(z),…, 1(z),…, i(z)), где i(z)), где  i(Z) – остаток полинома A(z) по модулю pi(z), i=(1,…, 7), a p1(z), р2(z), р3(z), p4(z), p5(z) – рабочие основания системы ПСКВ поля GF(25), р6(z), p7(z) – контрольные основания, отличающееся тем, что устройство содержит вход, который соединен с входами блока нулевизации, представляющего собой двухслойную нейронную сеть, первый слой которой содержит 31 нейрон, а второй слой – десять нейронов, выполняющих базовую операцию суммирования по модулю, входы первого нейрона второго слоя соединены с выходами 2, 8, 9, 11, 13, 14, 21, 22 нейронов первого слоя, входы второго нейрона второго слоя соединены с выходами 2, 9, 10, 12, 14, 15, 17, 23 нейронов первого слоя, входы третьего нейрона второго слоя соединены с выходами 1, 4, 7, 10, 14, 16, 18, 24 нейронов первого слоя, входы четвертого нейрона второго слоя соединены с выходами 5, 7, 9, 11, 12, 19, 21, 25 нейронов первого слоя, входы пятого нейрона второго слоя соединены с выходами 6, 7, 8, 10, 12, 13, 20, 26 нейронов первого слоя, входы шестого нейрона второго слоя соединены с выходами 2, 9, 11, 13, 18, 19, 20, 27 нейронов первого слоя, входы седьмого нейрона второго слоя соединены с выходами 3, 10, 12, 14, 17, 19, 20, 28 нейронов первого слоя, входы восьмого нейрона второго слоя соединены с выходами 4, 7, 9, 12, 15, 19, 20, 29 нейронов первого слоя, входы девятого нейрона второго слоя соединен с выходами 1, 5, 7, 8, 9, 10, 13, 14, 15, 16, 18, 19, 20, 30 нейронов первого слоя, входы десятого нейрона второго слоя соединен с выходами 6, 8, 10, 11, 12, 16, 17, 18, 20, 31 нейронов первого слоя, на входы блока нулевизации подают значения остатков i(Z) – остаток полинома A(z) по модулю pi(z), i=(1,…, 7), a p1(z), р2(z), р3(z), p4(z), p5(z) – рабочие основания системы ПСКВ поля GF(25), р6(z), p7(z) – контрольные основания, отличающееся тем, что устройство содержит вход, который соединен с входами блока нулевизации, представляющего собой двухслойную нейронную сеть, первый слой которой содержит 31 нейрон, а второй слой – десять нейронов, выполняющих базовую операцию суммирования по модулю, входы первого нейрона второго слоя соединены с выходами 2, 8, 9, 11, 13, 14, 21, 22 нейронов первого слоя, входы второго нейрона второго слоя соединены с выходами 2, 9, 10, 12, 14, 15, 17, 23 нейронов первого слоя, входы третьего нейрона второго слоя соединены с выходами 1, 4, 7, 10, 14, 16, 18, 24 нейронов первого слоя, входы четвертого нейрона второго слоя соединены с выходами 5, 7, 9, 11, 12, 19, 21, 25 нейронов первого слоя, входы пятого нейрона второго слоя соединены с выходами 6, 7, 8, 10, 12, 13, 20, 26 нейронов первого слоя, входы шестого нейрона второго слоя соединены с выходами 2, 9, 11, 13, 18, 19, 20, 27 нейронов первого слоя, входы седьмого нейрона второго слоя соединены с выходами 3, 10, 12, 14, 17, 19, 20, 28 нейронов первого слоя, входы восьмого нейрона второго слоя соединены с выходами 4, 7, 9, 12, 15, 19, 20, 29 нейронов первого слоя, входы девятого нейрона второго слоя соединен с выходами 1, 5, 7, 8, 9, 10, 13, 14, 15, 16, 18, 19, 20, 30 нейронов первого слоя, входы десятого нейрона второго слоя соединен с выходами 6, 8, 10, 11, 12, 16, 17, 18, 20, 31 нейронов первого слоя, на входы блока нулевизации подают значения остатков  i(z) соответственно, выходы блока нулевизации подключены соответственно ко входам блока памяти, содержащего константы ошибки, выходы которого подключены ко вторым входам семи корректирующих сумматоров соответственно, первые входы упомянутых сумматоров соединены со входом устройства, причем корректирующие сумматоры осуществляют суммирование поступающих на их первые входы значений i(z) соответственно, выходы блока нулевизации подключены соответственно ко входам блока памяти, содержащего константы ошибки, выходы которого подключены ко вторым входам семи корректирующих сумматоров соответственно, первые входы упомянутых сумматоров соединены со входом устройства, причем корректирующие сумматоры осуществляют суммирование поступающих на их первые входы значений  i(z) с соответствующими константами ошибки по основаниям pi(z), поступающими на вторые входы упомянутых сумматоров соответственно, выходы корректирующих сумматоров являются выходом устройства. i(z) с соответствующими константами ошибки по основаниям pi(z), поступающими на вторые входы упомянутых сумматоров соответственно, выходы корректирующих сумматоров являются выходом устройства.
РИСУНКИ
MM4A – Досрочное прекращение действия патента СССР или патента Российской Федерации на изобретение из-за неуплаты в установленный срок пошлины за поддержание патента в силе
Дата прекращения действия патента: 01.07.2007
Извещение опубликовано: 27.01.2009 БИ: 03/2009
|
|