|
(21), (22) Заявка: 2004137818/28, 19.05.2003
(24) Дата начала отсчета срока действия патента:
19.05.2003
(30) Конвенционный приоритет:
24.05.2002 (пп.1-19) US 60/383,209
(43) Дата публикации заявки: 27.05.2005
(46) Опубликовано: 27.05.2007
(56) Список документов, цитированных в отчете о
поиске:
ЕР 0745870 А, 04.12.1996. RU 2063639 С1, 10.07.1996. RU 2065182 C1, 10.08.1996. US 4340934 А, 20.07.1982.
(85) Дата перевода заявки PCT на национальную фазу:
24.12.2004
(86) Заявка PCT:
US 03/15882 (19.05.2003)
(87) Публикация PCT:
WO 03/100464 (04.12.2003)
Адрес для переписки:
129010, Москва, ул. Б.Спасская, 25, стр.3, ООО “Юридическая фирма Городисский и Партнеры”, пат.пов. Г.Б. Егоровой, рег.№ 513
|
(72) Автор(ы):
МУР Ян (AU),
КОСТОВ Клемент (US),
ИНГСТ Дэвид (US)
(73) Патентообладатель(и):
ВЕСТЕРНДЖЕКО САЙЗМИК ХОЛДИНГЗ ЛИМИТЕД (VG)
|
(54) ВЫСОКОРАЗРЕШАЮЩЕЕ ПРЕОБРАЗОВАНИЕ РАДОНА ДЛЯ ОБРАБОТКИ СЕЙСМИЧЕСКИХ ДАННЫХ
(57) Реферат:
Предложенные способ и компьютерная система относятся к геофизическим методам для обработки сейсмических данных. Сущность способа заключается в том, что находят высокоразрешающее преобразование Радона, предназначенное для применения к сейсмическим данным. Высокоразрешающее преобразование Радона регуляризируют, используя меру когерентности сейсмических данных. Предложено поддающееся оценке представление обработанных сейсмических данных. Мера когерентности сейсмических данных может включать в себя меру когерентности вдоль измерения сейсмических данных. Технический результат способа заключается в том, что сейсмические данные обрабатывают, используя высокоразрешающее преобразование Радона для улучшения требуемых признаков сейсмических данных. 4 н. и 15 з.п. ф-лы, 16 ил.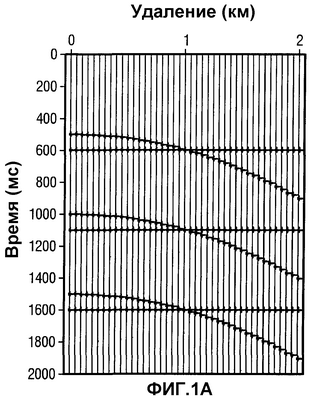
Область техники
Это изобретение относится к вычислению высокоразрешающих преобразований Радона, используемых при обработке сейсмических данных.
Описание уровня техники
Преобразования Радона, наряду с преобразованием Фурье и некоторыми другими преобразованиями, являются частью способов, доступных геофизикам для моделирования и анализа сейсмических сигналов. В геофизике и в других прикладных областях были получены усовершенствованные преобразования Радона благодаря преодолению ограничений, обусловленных дискретизацией и шумовым содержанием данных.
Самые первые преобразования Радона, использованные в геофизике, были просто дискретными версиями результатов, полученных для непрерывных функций, дискретизированных на протяжении большого интервала. Алгоритмы дискретного преобразования Радона, полученные позднее (Beylkin, 1987, Hampson, 1986), дают возможность осуществлять точно инвертируемые преобразования в случае дискретных выборочных данных с ограниченной апертурой. Эти преобразования, в настоящее время называемые обычными, являются эффективными при разделении сигнала и шума при условии, что входные данные и их линейные интегралы (то есть данные в области преобразования Радона) дискретизированы без наложения зеркальных частот. На практике обработка входных данных с наложенными зеркальными частотами является важным вопросом, и усовершенствования существующей в настоящее время технологии добиваются двумя способами.
Первый способ заключается в выработке требований к дискретизации применительно к обычному преобразованию Радона (Schonewille and Duijndam, 2001, Hugonnet and Canadas, 1995, Marfurt, 1996) и соблюдение этих требований во время регистрации данных, интерполяции данных и предварительной обработки (Manin and Spitz, 1995).
Во втором способе априорную информацию относительно частей данных, которые искажены вследствие наложения зеркальных частот, включают в вычисление преобразования Радона. В самом простейшем виде априорную информацию вводят в виде диагонального члена регуляризации в решение методом наименьших квадратов для преобразования Радона. Когда все значения вдоль диагонали равны, результирующие решения в общем случае не позволяют разрешать неоднозначности, обусловленные входными данными с наложенными зеркальными частотами. Nichols (1992a, 1992b), Herrmann et al. (2000) и Hugonnet (2001) показали, что при соответствующей диагональной регуляризации получаются точные и эффективные преобразования Радона даже в случае, когда входные данные искажены вследствие наложения зеркальных частот.
В рамках оценки Байеса диагональная регуляризация может быть интерпретирована как постановка априорных распределений Гаусса в соответствие параметрам преобразования, в отношении которых также предполагается, что они должны быть статистически независимыми (Tarantola, 1987, Ulrych et al., 2001). Для других алгоритмов требуется меньше априорной информации благодаря исключению предположения относительно распределений Гаусса, но выражена тенденция к большей вычислительной сложности (Sacchi and Ulrych, 1995, Harlan et al., 1984, Thorson and Claerbout, 1985).
В предшествующем уровне техники относительно диагональной регуляризации при вычислении высокоразрешающих преобразований Радона имеются способы, которые описали Nichols (1992a), Herrmann et al. (2000) и Hugonnet et al. (2001). В этих случаях, исходя из соображений вычислительной эффективности, преобразование обычно применяют в пространственно-частотной области с зависимой от частоты диагональной регуляризацией. Однако член регуляризации не корректируют в зависимости от вычисленного преобразования Радона.
Nichols (1992a) получил веса регуляризации из меры когерентности вдоль временной оси частот данных. Мера когерентности для не искаженной зеркальными частотами сейсмической энергии обычно изменяется медленно с частотой. С другой стороны, сильные мелкомасштабные изменения меры когерентности часто используют для идентификации энергии, искаженной зеркальной частотами. Для получения весов Nichols (1992a) предложил сглаживание меры когерентности на интервале частот, содержащем частоты, которые ниже и выше частоты, подлежащей обработке.
Herrmann (2000) и Hugonnet (2001) получили веса рекурсивно на частоте, начиная с обычного преобразования Радона на самых низких частотах. Веса для частоты, на которой выполняют обработку, образуют по результатам высокоразрешающего преобразования Радона на более низких частотах.
Примерами на фиг.2, 3 и 4 иллюстрируются преобразования Радона, вычисленные при использовании различных схем регуляризации из предшествующего уровня техники. Фиг.2a-2d соответствуют обычному преобразованию Радона, регуляризированному с помощью скаляра, умноженного на единичную матрицу. На фиг.3a-3d веса регуляризации являются переменными членами вдоль диагонали, а соответствующее решение имеет более высокое разрешение. Однако на фиг.4 видно, что та же самая схема регуляризации, примененная к загрязненным шумом данным, дает субоптимальный результат.
Веса на фиг.4е не позволяют обнаруживать параболические оси синфазности волны на низких и высоких частотах. Веса надежно отображают приращения времени в данных только выше 15 кГц, тогда как в случае отсутствия шума, показанном на фиг.3е, приращения времени обнаруживаются от примерно 5 кГц. Кроме того, веса на фиг.4е имеют кажущиеся высокие значения на краях области преобразования, возможно шумы, обусловленные началом преобразования с обычного преобразования Радона (то есть с равными весами). Этими высокими значениями вызываются сильные шумы в области данных.
Описан новый способ для получения весов регуляризации, предназначенных для вычисления высокоразрешающего преобразования Радона.
В одном варианте осуществления изобретения представлен способ обработки сейсмических данных. Для применения к сейсмическим данным находят высокоразрешающее преобразование Радона. Высокоразрешающее преобразование Радона регуляризируют, используя меру когерентности сейсмических данных. Сейсмические данные обрабатывают, используя высокоразрешающее преобразование Радона для улучшения желательных признаков сейсмических данных. Предлагают поддающееся оценке представление обработанных сейсмических данных.
Мера когерентности сейсмических данных может включать в себя меру когерентности вдоль измерения сейсмических данных. Сейсмические данные могут быть подразделены в двумерный массив, который включает в себя одно измерение времени или глубины, и второе измерение из положения пространственной поверхности или угла. Кроме того, сейсмические данные могут быть подразделены в двумерный массив, включающий в себя одно измерение, включающееся в себя время или глубину, и другое измерение, выбранное из положений пространственной поверхности и углов.
Обработка сейсмических данных может включать в себя выполнение высокоразрешающего преобразования Радона относительно сейсмических данных при использовании меры когерентности сейсмических данных. Могут быть выделены первая область и вторая область в сейсмических данных, подвергнутых преобразованию Радона. Может быть выполнена инверсия высокоразрешающего преобразования Радона относительно выделенных, подвергнутых преобразованию Радона сейсмических данных.
Первая область может быть сигнальной областью, а вторая область может быть шумовой областью. Измерения сейсмических данных могут включать в себя многочисленные измерения сейсмических данных. Измерение сейсмических данных может также включать в себя частотную область.
В другом варианте осуществления изобретения обработка сейсмических данных при использовании высокоразрешающего преобразования Радона для улучшения требуемых признаков сейсмических данных может дополнительно включать в себя аппроксимацию комплексной траектории приращения времени отрезками. Сейсмические данные могут быть подразделены в локальные окна данных, согласованных с отрезками. Высокоразрешающее преобразование Радона может быть выполнено в каждом из локальных окон данных для улучшения требуемых признаков сейсмических данных, согласованных с отрезками. Осуществление высокоразрешающего преобразования Радона в каждом из локальных окон данных может включать в себя этапы вычисления преобразования с периодическими граничными условиями и применения разделения сигнала и шума, согласованного с нулевыми граничными условиями при использовании известных временных сдвигов между компонентами модели.
Регуляризация высокоразрешающего преобразования Радона при использовании меры когерентности сейсмических данных может включать в себя вычисление матрицы регуляризации, которое включает в себя применение фазового сдвига, определенного с помощью траектории приращения времени, к сейсмическим данным. Кроме того, она может включать в себя нормализацию мощности разреза вдоль траектории приращения времени для получения меры когерентности. Она также может включать в себя обострение меры когерентности или сглаживание меры когерентности по второму измерению сейсмических данных. Второе измерение сейсмических данных может включать в себя измерение, выбранное из пространственного положения и угла.
В другом варианте осуществления изобретение может быть реализовано посредством компьютерной системы, при этом компьютер включает в себя запоминающее устройство и процессор и выполняемое программное обеспечение, находящееся в запоминающем устройстве компьютера. Программное обеспечение работает совместно с процессором для нахождения высокоразрешающего преобразования Радона, предназначенного для применения к сейсмическим данным. Высокоразрешающее преобразование Радона регуляризируется при использовании меры когерентности сейсмических данных. Сейсмические данные обрабатываются при использовании высокоразрешающего преобразования Радона для улучшения требуемых признаков сейсмических данных.
Кроме того, программное обеспечение предусмотрено для осуществления высокоразрешающего преобразования Радона относительно сейсмических данных при использовании меры когерентности сейсмических данных. В сейсмических данных, подвергнутых преобразованию Радона, могут быть выделены первая область и вторая область. Относительно выделенных, подвергнутых преобразованию Радона сейсмических данных может быть использована инверсия высокоразрешающего преобразования Радона.
Программное обеспечение может также обеспечивать выполнение аппроксимации сложной траектории приращения времени отрезками. Сейсмические данные могут быть подразделены в локальные окна данных, согласованных с отрезками. Высокоразрешающее преобразование Радона может быть выполнено в каждом из локальных окон данных для улучшения требуемых признаков сейсмических данных, согласованных с большим числом отрезков.
В предложенном способе могут сохраняться характеристики разрешающей способности и исключения наложения зеркальных частот высокоразрешающих преобразований Радона и наибольшей эффективности способов, которые предложили Nichols и Herrmann, но способ может быть более устойчивым по сравнению с тем, который предложил Herrmann, и может обеспечивать лучшее разрешение по сравнению со способом, который предложит Nichols.
Описание чертежей
Другие признаки и преимущества изобретения станут более понятными при принятии во внимание нижеследующего описания с сопроводительными чертежами.
На чертежах:
Фиг.1 – (a) – синтетические тестовые данные, включающие в себя параболические оси синфазности волны с приращениями времени 0 и 400 мс при максимальном удалении 2000 м; (b) – тот же самый набор данных с добавленным случайным шумом;
Фиг.2 – иллюстрация подавления многократных волн обычным преобразованием Радона, примененным к данным из фиг.1a, свободным от шума; (А) – оцененные однократные волны; (В) – оцененные многократные волны; (С) – остаток: разность между входными данными и результатом применения к входным данным прямого и обратного преобразований Радона; и (D) – область Радона;
Фиг.3 – иллюстрация применения к данным из фиг.1a, свободным от шума, подавления многократных волн высокоразрешающим преобразованием Радона при использовании рекурсивного метода для получения весов; фиг. с (a) по (d) соответствуют фиг.2; на последней фиг.(e) показаны веса, использованные для высокоразрешающего преобразования Радона; веса отображены в зависимости от частоты (вертикальная ось) и параметра приращения времени (горизонтальная ось);
Фиг.4 – изображения, соответствующие фиг.3, но для зашумленных синтетических данных, показанных на фиг.1b;
Фиг.5 – изображения, соответствующие фиг.3, но при использовании весов, полученных на основе меры когерентности;
Фиг.6 – увеличенные изображения из фиг.4b (слева рекурсивная корректировка весов) и 5b (справа веса на основе меры когерентности);
Фиг.7 – изображения с плохой фокусировкой и шумами преобразования, связанными с обработкой гиперболической оси синфазности при использовании одного глобального окна данных и параболического преобразования Радона; (а) – остаток; (b) – данные в области параболического преобразования Радона; (с) – веса, использованные для высокоразрешающего преобразования Радона;
Фиг.8 – графики, иллюстрирующие отображение локального окна время-удаление в области параболического преобразования Радона;
Фиг.9 – результаты обработки тех же самых входных данных, что и на фиг.7, в пределах трех отдельных окон удалений; (а) – разность между входными данными и результатом прямого и обратного преобразований Радона, примененных к входным данным; (b, c, d) – данные в области параболического преобразования Радона для каждого из трех окон входных данных; (e, f, g) – веса, использованные для высокоразрешающего преобразования Радона для случаев каждого из трех окон входных данных;
Фиг.10 – пример полевых данных, обработка путем обычного преобразования Радона; (а) – входные данные; (b) – оцененные однократные волны; (с) – оцененные многократные волны; (d) – входные данные минус оцененные однократные волны; (е) – остаток от прямого и обратного преобразований: входные данные минус сумма оцененных однократных волн и многократных волн; (f) – данные в области параболического преобразования Радона;
Фиг.11 – пример полевых данных, как на фиг.10, при этом веса вычислены рекурсивно;
Фиг.12 – пример полевых данных, как на фиг.10, при этом веса определены на основе меры когерентности;
Фиг.13 – иллюстрация сравнения весов: (13а, слева) способ на основе меры когерентности и (13b, справа) рекурсивный способ;
Фиг.14 – рабочая диаграмма способа преобразования Радона;
Фиг.15 – (а) – сечения данных со схематичным отображением локальных окон данных в пределах каждого сечения, подготовленного для ввода в двумерное преобразование Радона; (b) – схематичное представление оси синфазности сейсмических данных волны (криволинейной формы) и траекторий приращения времени (прямые линии) для преобразования Радона; (с) схематичное представление области преобразования Радона. После суммирования вдоль прямых линий вертикальная линия в области преобразования будет закрашиваться, а большая часть энергии будет вноситься из траектории приращения времени, которые являются касательными по отношению к оси синфазности; и
Фиг.16 – рабочая диаграмма способа обработки сейсмических данных.
В настоящем изобретении представлена новая схема для вычисления регуляризованного высокоразрешающего преобразования Радона.
Что касается фиг.16, то сейсмические данные регистрируют 1601, используя стандартные промышленные способы и группируя их по методу общей поверхности (например, в виде сейсмограммы общей глубинной точки) или приповерхностной точки (например, в виде угловых сейсмограмм, образованных во время миграции). На фиг.15а показан двумерный массив 1502, образованный путем группирования по одному измерению в виде времени или глубины и по другому измерению в виде пространственного положения (удаления) или угла. Измерение времени или глубины обычно дискретизировано с большой плотностью и без наложения зеркальных частот, тогда как наложение зеркальных частот может наблюдаться вследствие недостаточной дискретизации вдоль пространственного положения (удаления) или углового измерения данных. В других вариантах осуществления с помощью группировок различных видов можно создавать для обработки трехмерные или более высокого порядка массивы.
Для преобразования данных траектории приращения времени для преобразования Радона выбирают 1602, используя приращение времени волн в данных и выводы, касающиеся вычислительной эффективности. Как показано на фиг.15b и 15с, типовыми вариантами траекторий приращения времени являются линейные и параболические траектории. Другие траектории приращений времени, такие, как гиперболические или более сложные траектории, также могут быть выбраны.
Во время преобразования Радона данные преобразуют 1605 в частотную область в пределах хорошо дискретизированного измерения (времени или глубины). Вектор входных данных для преобразования Радона на частоте  обозначают d(x, обозначают d(x,  ), кратко d. Данные индексируют положениями в пространстве, x, часто представляемыми в виде расстояния (удаления) между источником и приемником. Вектор d данных может представлять данные из всей сейсмограммы или из локального (время-удаление) окна данных 1501, показанных на фиг.15а. Конкретные вопросы, относящиеся к обработке в локальных окнах данных рассмотрены ниже в разделе под названием “Критерии для разделения сигнала и шума в локальных окнах данных”. ), кратко d. Данные индексируют положениями в пространстве, x, часто представляемыми в виде расстояния (удаления) между источником и приемником. Вектор d данных может представлять данные из всей сейсмограммы или из локального (время-удаление) окна данных 1501, показанных на фиг.15а. Конкретные вопросы, относящиеся к обработке в локальных окнах данных рассмотрены ниже в разделе под названием “Критерии для разделения сигнала и шума в локальных окнах данных”.
Результатом преобразования Радона на частоте  является вектор m(q, является вектор m(q,  ) или кратко m, также называемый модельным вектором. Элементы m индексируют параметрами q, определяющими выбранные траектории приращения времени преобразования Радона. В случае параболического преобразования Радона параметры q интерпретируют как кривизны парабол при нулевом удалении. Обычно данные, вводимые в преобразование, представляют собой двумерные сечения. Однако описание методов преобразования Радона, использованных в некоторых вариантах осуществления настоящего изобретения, применимо к данным с большим числом измерений, и в этом случае параметры кривизны больше не являются скалярами, а векторами. ) или кратко m, также называемый модельным вектором. Элементы m индексируют параметрами q, определяющими выбранные траектории приращения времени преобразования Радона. В случае параболического преобразования Радона параметры q интерпретируют как кривизны парабол при нулевом удалении. Обычно данные, вводимые в преобразование, представляют собой двумерные сечения. Однако описание методов преобразования Радона, использованных в некоторых вариантах осуществления настоящего изобретения, применимо к данным с большим числом измерений, и в этом случае параметры кривизны больше не являются скалярами, а векторами.
Преобразование Радона является линейным преобразованием относительно данных и модельных векторов. Связь между векторами модели и данных может быть выражена в матричной форме с помощью уравнения 1 (Beylkin, 1987):
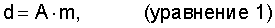
где А – матрица размера (M, N);
М – число элементов (комплексных скаляров) в векторе d данных; и
N – число элементов в модельном векторе m.
Преобразование Радона можно найти как решение системы линейных уравнений, определенной в уравнении (1). Чтобы гарантировать единственное и устойчивое решение системы линейного уравнения (1), обычно задают целевую функцию, J(m), связанную с уравнением (1), которая является суммой члена регуляризации и члена подбора данных:
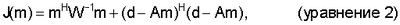
где верхний индекс Н означает сопряженную транспозицию вектора или матрицы; и
W-1 – матрица регуляризации.
Наиболее общим выбором для W-1 является диагональная матрица с постоянными элементами по диагонали, например W-1= I, где I является единичной матрицей N×N. Этот выбор регуляризации связан с обычным преобразованием Радона и называется методом “затухающих наименьших квадратов”. Он обеспечивает получение устойчивого решения, но требует не искаженных дискретизацией входных данных с большой апертурой. I, где I является единичной матрицей N×N. Этот выбор регуляризации связан с обычным преобразованием Радона и называется методом “затухающих наименьших квадратов”. Он обеспечивает получение устойчивого решения, но требует не искаженных дискретизацией входных данных с большой апертурой.
В одном варианте осуществления настоящего изобретения веса регуляризации получают вычислением 1603 меры когерентности вдоль оси удаления:
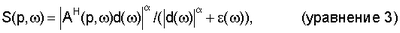
где АН – матрица сопряженной транспозиции относительно А;
d( ) – вектор данных может содержать данные из всей сейсмограммы или из локального окна время-удаление сейсмограммы; ) – вектор данных может содержать данные из всей сейсмограммы или из локального окна время-удаление сейсмограммы;
 – коэффициент, который используют для повышения обострения меры когерентности; и – коэффициент, который используют для повышения обострения меры когерентности; и
 – множитель придания устойчивости и/или нормировочный. – множитель придания устойчивости и/или нормировочный.
Матрицу сопряженной транспозиции относительно А задают в членах траекторий приращения времени, а в данные вводят соответствующие фазовые сдвиги.
Затем меру когерентности можно сгладить в полосе частот, используя стандартную схему взвешенного усреднения (Marple, 1987), при этом элементы диагональной весовой матрицы W вычисляют как:
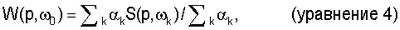
где коэффициенты  k зависят от числа частот, используемых при сглаживании, а не от действительных значений частот k зависят от числа частот, используемых при сглаживании, а не от действительных значений частот  0, 0,  1 и т.д. 1 и т.д.
Типовыми вариантами для коэффициентов  k являются постоянные, треугольные и гауссовы веса. Предпочтительно, чтобы диапазон частот, в котором сглаживают меру когерентности, предпочтительно был широкой полосой частот и включал в себя высокие частоты. Для получения диагональной весовой матрицы, основанной на мере когерентности, могут быть использованы сглаживающие функции других видов, известные специалистам в области техники, к которой относится изобретение. k являются постоянные, треугольные и гауссовы веса. Предпочтительно, чтобы диапазон частот, в котором сглаживают меру когерентности, предпочтительно был широкой полосой частот и включал в себя высокие частоты. Для получения диагональной весовой матрицы, основанной на мере когерентности, могут быть использованы сглаживающие функции других видов, известные специалистам в области техники, к которой относится изобретение.
В дополнение к этому, аналогично обычной практике обработки сейсмических данных, меру когерентности можно подвергнуть фильтрации для повышения устойчивости путем пространственного усреднения по небольшому числу соседних положений общей глубинной точки или путем отбрасывания значений меры когерентности, меньших порогового значения.
После преобразования 1605 сейсмических данных при использовании высокоразрешающего преобразования Радона могут быть выделены сигнальные и шумовые области преобразованных данных (это также известно как мьютинг). Простейший способ заключается в выборе вручную геометрии разделения (функции мьютинга) сигнальных и шумовых областей и удаления данных на одной стороне геометрии. Если сейсмические данные выделяют в локальных окнах, мьютинг можно осуществлять способом, описанным в разделе под названием “Эффективное осуществление выделения (мьютинга) сигнала и шума для преобразований из локальных окон данных”.
После удаления шума сейсмические данные повторно преобразуют 1607, используя обратное высокоразрешающее преобразование Радона. Затем сейсмические данные могут быть представлены 1608 в виде поддающегося оценке представления, например на компьютерной распечатке или на экране дисплея, или обработаны дополнительно до отображения или представления пользователю.
В различных вариантах осуществления этого изобретения программное обеспечение в компьютере или компьютерной системе можно использовать для осуществления высокоразрешающего преобразования Радона, представленного в этом изобретении и известного в области техники, к которой относится изобретение.
Параболическое преобразование Радона основано на волнах в данных, имеющих параболическое приращение времени и постоянную амплитуду после введения поправки на нормальное приращение времени. Однако на практике траектории приращения времени в данных являются сложными и необязательно параболическими. В другом варианте осуществления этого изобретения сложная траектория приращения времени может быть аппроксимирована путем объединения локальных отрезков парабол. Рассмотрение, приведенное ниже, относится к параболам, но применимо к любым отрезкам, обычно используемым при преобразованиях Радона.
Локальные окна данных определяют путем деления каждого измерения данных на отрезки, которые перекрывают весь диапазон этого измерения. Параболическое преобразование Радона может быть применено к данным в каждом из локальных окон. В случае, когда параболическое преобразование Радона применяют в каждом локальном окне, предположения относительно параболического приращения времени и постоянной амплитуды удовлетворяются лучше, чем в пределах всего диапазона этого измерения. В отличие от обычного преобразования Радона использование высокоразрешающего параболического преобразования Радона обеспечивает возможность отделения в локальном окне сигнала от шумовых данных. Используя отрезки парабол, которыми сложная траектория хорошо аппроксимируется в пределах локального окна, можно эффективно выразить разделение сигнала и шума в зависимости от сложной траектории приращения времени. Благодаря моделированию сложных траекторий приращения времени критерий для выбора требуемых признаков в данных может быть более эффективным.
На фиг.7 показана сейсмическая волна с остаточным гиперболическим приращением времени, которая плохо сфокусирована в случае параболического преобразования Радона, вычисленного по всему диапазону удалений. После разделения диапазона удалений на три части и вычисления параболического преобразования Радона отдельно в пределах каждой части каждое из преобразований оказывается хорошо сфокусированным, что показано на фиг.9.
Однако отметим, что при каждом из зависящих от диапазона удалений преобразований на фиг.9 гипербола фокусируется несколько в ином месте в пространстве модели. Наилучшие подобранные параболы в каждом окне удаления имеют несколько иные параметры (кривизну и время пробега по нормальному лучу). Это заключение подразумевает, что функции мьютинга, используемые для разделения волн в области преобразования, должны также изменяться как функция диапазона удаления данных, используемых для вычисления преобразования.
Для управления изменениями параметров мьютинга с удалением применим следующий подход. Во-первых, начнем с функции мьютинга, q( ,x=0), для окна, включающего в себя нулевое удаление. При заданном времени ,x=0), для окна, включающего в себя нулевое удаление. При заданном времени  пробега по нормальному лучу обозначим через q0 соответствующее положение мьютинга, q0=q( пробега по нормальному лучу обозначим через q0 соответствующее положение мьютинга, q0=q( ,x=0). Параметрами ( ,x=0). Параметрами ( ,q0) задается парабола t= ,q0) задается парабола t= +q0x2/xmax 2, а также и гипербола с тем же временем пробега по нормальному лучу и кривизной при нулевом удалении, что и парабола: +q0x2/xmax 2, а также и гипербола с тем же временем пробега по нормальному лучу и кривизной при нулевом удалении, что и парабола:
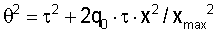
В таком случае соотношение для мьютингов между окнами удалений:
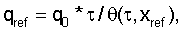
где qref – требуемое положение мьютинга для окна данных, связанных с удалением xref, и для времени  пробега по нормальному лучу. пробега по нормальному лучу.
Параметр qref приращения времени получают путем согласования в точке xref градиентов параболы ( ,qref) и гиперболы ( ,qref) и гиперболы ( ,q0). ,q0).
В более общем случае с помощью процедуры, описанной выше, находятся локальные критерии разделения сигнала и шума, согласованные с глобальным критерием разделения сигнала и шума и выраженные в членах сложной (например, гиперболической) функции мьютинга. Новым признаком по сравнению с предшествующим уровнем техники является использование траектории приращения времени (например, гиперболической) для глобального критерия разделения сигнала и шума, которая не является частью траекторий приращения времени, используемых для вычисления преобразования Радона (например, параболических). Использование этого нового признака увеличивает гибкость и повышает точность разделения сигнала и шума при сохранении вычислительной эффективности. Фактически при улучшенном разделении сигнала и шума может улучшаться разделение требуемых признаков в сейсмических данных.
Согласно другому варианту осуществления этого изобретения может быть вычислен оптимальный временной сдвиг между окнами в области (x-t) данных и в области (q,  ) преобразования Радона, как показано на фиг.8. ) преобразования Радона, как показано на фиг.8.
Рассмотрим окно время-удаление, задаваемое временным интервалом [t1, t2] и интервалом [x1, x2] удалений, и предположим, что xref является соответствующим эталонным удалением для окна (обычно это центральное удаление). Для заданного значения q времена пробега по нормальному лучу параболы, которая пересекает эталонное удаление, в пределах окна лежат в интервале [ 1, 1,  2], где 2], где  1=t1– 1=t1–  (q) и (q) и  2=t2– 2=t2–  (q), при этом (q), при этом   (q)=q·xref 2/xmax 2. Можно видеть, что оптимальное окно в (q)=q·xref 2/xmax 2. Можно видеть, что оптимальное окно в  является предшествующим (для положительного q) в сопоставлении с оптимальным окном в t на величину временного сдвига является предшествующим (для положительного q) в сопоставлении с оптимальным окном в t на величину временного сдвига   (q). Отметим, что временной сдвиг является линейным от q, и поэтому прямоугольное окно в t-x описывается параллелограммом в (q). Отметим, что временной сдвиг является линейным от q, и поэтому прямоугольное окно в t-x описывается параллелограммом в  -q. Когда q и xref большие, временной сдвиг -q. Когда q и xref большие, временной сдвиг   может быть значительно больше, чем длина окна во временной области. может быть значительно больше, чем длина окна во временной области.
Поскольку при обработке в частотной области подразумевается, что данные и модель являются периодическими с периодом t2-t1, модель является эффективно определенной во все моменты времени, и мы просто выбираем соответствующее (в виде параллелограмма) окно из этой модели, зная сдвиг   (q). Фактически процедура, описанная здесь, позволяет эффективно вычислять преобразование, используя периодические граничные условия, наряду с применением разделения сигнала и шума, как если бы граничные условия имели нулевые значения (предпочтительное описание) за пределами интервала [t1, t2] входных данных. (q). Фактически процедура, описанная здесь, позволяет эффективно вычислять преобразование, используя периодические граничные условия, наряду с применением разделения сигнала и шума, как если бы граничные условия имели нулевые значения (предпочтительное описание) за пределами интервала [t1, t2] входных данных.
Для иллюстрации вариантов осуществления этого изобретения на фиг.1b показаны синтетические (с добавлением случайного шума). Для случая данных с добавленным шумом результаты отображены на фиг.5а-5е. Веса, основанные на мере когерентности, получены в частотном диапазоне от 70 до 90 Гц, и они предполагаются постоянными во всей полосе частот. В данном случае разделение однократных волн и многократных волн улучшено благодаря более точным весам. При этом на краях области преобразования высокие значения отсутствуют.
Результаты из фиг.4b и 5b в большем масштабе отражены на фиг.6. Ясно видно улучшенное разделение однократных волн и многократных волн при использовании весов на основе меры когерентности (фиг.6b), а не рекурсивно корректируемых весов (фиг.6а).
В качестве полевых данных для этого примера использована сейсмограмма общей глубинной точки (фиг.10а) с шагом между трассами 100 м и максимальным удалением около 6 км. Результаты обычного преобразования Радона (фиг.10b-10f) показывают, что встречаются обычные проблемы: плохая фокусировка в области преобразования, значительная энергия на краях области преобразования, шумы дискретизации в областях преобразования и данных.
Результаты, полученные на основании настоящего изобретения, отображены на фиг.12b-12f. Соответствующие веса на основе меры когерентности показаны на фиг.13а. Как и ожидалось, шумы дискретизации и преобразования снижены, а оцененные однократные волны (фиг.12b) улучшены по сравнению с результатами, полученными на основании обычного преобразования Радона (фиг.10b).
Результаты для высокоразрешающего преобразования Радона при использовании рекурсивно корректируемых весов отображены на фиг.11а-11f, при этом соответствующие веса показаны на фиг.13b. Эти результаты не столь хороши, как результаты, полученные с весами на основе меры когерентности. Это особенно видно на фиг.11f (область преобразования) и 11b (оцененные однократные волны), где часть энергии помех дискретизации и шумов на краях области преобразования теперь снова видна и может быть отнесена на счет субоптимальных весов, оцененных с помощью рекурсивной схемы (фиг.13b).
Описаны несколько вариантов осуществления настоящего изобретения. Тем не менее должно быть понятно, что различные модификации могут быть сделаны без отступления от сущности и объема изобретения. Поэтому другие варианты осуществления находятся в рамках объема нижеследующей формулы изобретения.
Формула изобретения
1. Способ обработки сейсмических данных, включающий в себя
измерение сейсмических данных, при этом указанные данные подразделяют в двумерный массив, содержащий одно измерение, выбранное из группы, состоящей из времени и глубины, и второе измерение, выбранное из группы, состоящей из пространственного положения поверхности и угла,
нахождение высокоразрешающего преобразования Радона для применения к сейсмическим данным, включающее в себя
регуляризацию высокоразрешающего преобразования Радона при использовании меры когерентности сейсмических данных и
обработку сейсмических данных при использовании высокоразрешающего преобразования Радона для улучшения требуемых признаков сейсмических данных; и
обеспечение поддающегося оценке представления обработанных сейсмических данных.
2. Способ по п.1, в котором мера когерентности сейсмических данных содержит меру когерентности вдоль измерения сейсмических данных.
3. Способ по п.1, в котором сейсмические данные подразделяют в массив, содержащий одно измерение, выбранное из группы, состоящей из времени и глубины, и второе измерение, содержащее большее количество измерений, выбранных из группы, состоящей из положения пространственной поверхности и углов.
4. Способ по п.1, в котором обработка сейсмических данных дополнительно включает в себя
выполнение высокоразрешающего преобразования Радона относительно сейсмических данных при использовании меры когерентности сейсмических данных;
выделение первой области и второй области в сейсмических данных, подвергнутых преобразованию Радона; и
выполнение инверсии высокоразрешающего преобразования Радона относительно выделенных подвергнутых преобразованию Радона сейсмических данных.
5. Способ по п.3, в котором первая область представляет собой сигнальную область, а вторая область представляет собой шумовую область.
6. Способ по п.2, в котором измерение сейсмических данных содержит большое количество измерений сейсмических данных.
7. Способ по п.2, в котором измерение сейсмических данных содержит частотную область.
8. Способ по п.1, в котором обработка сейсмических данных при использовании высокоразрешающего преобразования Радона для улучшения требуемых признаков сейсмических данных дополнительно включает в себя
аппроксимацию сложной траектории приращения времени большим количеством отрезков;
разделение сейсмических данных в большое количество локальных окон данных, согласованных с большим количеством отрезков; и
выполнение высокоразрешающего преобразования Радона в каждом из локальных окон данных для улучшения требуемых признаков сейсмических данных, согласованных с большим количеством отрезков.
9. Способ по п.8, в котором выполнение высокоразрешающего преобразования Радона в каждом из локальных окон данных дополнительно включает в себя этапы вычисления преобразования с периодическими граничными условиями и применения разделения сигнала и шума, согласованного с нулевыми граничными условиями при использовании известных временных сдвигов между компонентами модели.
10. Способ по п.1, в котором регуляризация высокоразрешающего преобразования Радона при использовании меры когерентности сейсмических данных дополнительно включает в себя вычисление матрицы регуляризации, включающее в себя применение фазового сдвига, определенного с помощью траектории приращения времени, к сейсмическим данным.
11. Способ по п.1, в котором регуляризация высокоразрешающего преобразования Радона при использовании меры когерентности сейсмических данных дополнительно включает в себя нормализацию мощности разреза вдоль траектории приращения времени для получения меры когерентности.
12. Способ по п.1, в котором регуляризация высокоразрешающего преобразования Радона при использовании меры когерентности сейсмических данных дополнительно включает в себя обострение меры когерентности.
13. Способ по п.1, в котором регуляризация высокоразрешающего преобразования Радона при использовании меры когерентности сейсмических данных дополнительно включает в себя сглаживание меры когерентности по второму измерению сейсмических данных.
14. Способ по п.13, в котором второе измерение сейсмических данных содержит измерение, выбранное из пространственного положения и угла.
15. Способ для обработки сейсмических данных, включающий в себя
измерение сейсмических данных, при этом указанные данные подразделяют в двумерный массив, содержащий одно измерение, выбранное из группы, состоящей из времени и глубины, и второе измерение, выбранное из группы, состоящей из пространственного положения поверхности и угла,
нахождение высокоразрешающего преобразования Радона для применения к сейсмическим данным, включающее в себя
регуляризацию высокоразрешающего преобразования Радона при использовании меры когерентности вдоль измерения указанных сейсмических данных, при этом измерение сейсмических данных содержит частотную область;
обработку сейсмических данных при использовании высокоразрешающего преобразования Радона для улучшения требуемых признаков сейсмических данных, при этом обработка сейсмических данных включает в себя
выполнение высокоразрешающего преобразования Радона относительно сейсмических данных при использовании меры когерентности;
выделение сигнальной области и шумовой области в сейсмических данных, подвергнутых преобразованию Радона;
выполнение инверсии высокоразрешающего преобразования Радона относительно выделенных подвергнутых преобразованию Радона сейсмических данных и
обеспечение поддающегося оценке представления обработанных сейсмических данных.
16. Компьютерная система для обработки сейсмических данных, содержащая
компьютер, при этом компьютер содержит запоминающее устройство и процессор; и
реализующее программное обеспечение, находящееся в запоминающем устройстве компьютера, при этом программное обеспечение работает совместно с процессором для
нахождения высокоразрешающего преобразования Радона для применения к сейсмическим данным, полученным при измерении, при этом указанные данные подразделяют в двумерный массив, содержащий одно измерение, выбранное из группы, состоящей из времени и глубины, и второе измерение, выбранное из группы, состоящей из пространственного положения поверхности и угла,
при этом указанное преобразование Радона включает в себя
регуляризацию высокоразрешающего преобразования Радона при использовании меры когерентности сейсмических данных и
обработки сейсмических данных при использовании преобразования Радона для улучшения требуемых признаков сейсмических данных.
17. Система по п.16, в которой обработка сейсмических данных при использовании высокоразрешающего преобразования Радона дополнительно включает в себя
выполнение высокоразрешающего преобразования Радона относительно сейсмических данных при использовании меры когерентности сейсмических данных;
выделение первой области и второй области в сейсмических данных, подвергнутых преобразованию Радона; и
выполнение инверсии высокоразрешающего преобразования Радона относительно выделенных подвергнутых преобразованию Радона сейсмических данных.
18. Компьютерная система по п.16, в которой обработка сейсмических данных при использовании высокоразрешающего преобразования Радона дополнительно включает в себя
аппроксимацию сложной траектории приращения времени большим количеством отрезков;
разделение сейсмических данных в большое количество локальных окон данных, согласованных с большим количеством отрезков; и
выполнение высокоразрешающего преобразования Радона в каждом из локальных окон данных для улучшения требуемых признаков сейсмических данных, согласованных с большим количеством отрезков.
19. Компьютерная система для обработки сейсмических данных, содержащая
компьютер, при этом компьютер содержит запоминающее устройство и процессор; и
средство для обработки сейсмических данных на компьютере, полученных при измерении, при этом указанные данные подразделяют в двумерный массив, содержащий одно измерение, выбранное из группы, состоящей из времени и глубины, и второе измерение, выбранное из группы, состоящей из пространственного положения поверхности и угла, при использовании высокоразрешающего преобразования Радона и меры когерентности сейсмических данных для улучшения требуемых признаков сейсмических данных.
РИСУНКИ
MM4A – Досрочное прекращение действия патента СССР или патента Российской Федерации на изобретение из-за неуплаты в установленный срок пошлины за поддержание патента в силе
Дата прекращения действия патента: 20.05.2007
Извещение опубликовано: 27.08.2008 БИ: 24/2008
NF4A – Восстановление действия патента СССР или патента Российской Федерации на изобретение
Дата, с которой действие патента восстановлено: 27.07.2010
Извещение опубликовано: 27.07.2010 БИ: 21/2010
|