| На основании пункта 3 статьи 13 Патентного закона Российской Федерации от 23 сентября 1992 г. № 3517-I патентообладатель обязуется передать исключительное право на изобретение (уступить патент) на условиях, соответствующих установившейся практике, лицу, первому изъявившему такое желание и уведомившему об этом патентообладателя и федеральный орган исполнительной власти по интеллектуальной собственности, – гражданину РФ или российскому юридическому лицу. |
|
(21), (22) Заявка: 2005134305/28, 07.11.2005
(24) Дата начала отсчета срока действия патента:
07.11.2005
(46) Опубликовано: 27.05.2007
(56) Список документов, цитированных в отчете о
поиске:
RU 2156959 C1, 27.09.2000. Авиационные приборы и навигационные системы. / Под ред. Бабича О.А. – М.: ВВИА им. Н.Е.Жуковского, 1981, с.525-529. RU 2115128 C1, 10.07.1998. RU 2184937 C1, 19.12.2000. Гироскопические системы / Под ред. Д.С.Пельпора. – М.: Высшая школа, 1986, с.64-65.
Адрес для переписки:
355021, г.Ставрополь, ул. Ленина, 320, СВВАИУ (ВИ), НИО, А.В. Захарину
|
(72) Автор(ы):
Захарин Александр Викторович (RU),
Шепеть Игорь Петрович (RU),
Хабаров Алексей Николаевич (RU),
Демчук Анжела Анатольевна (RU),
Онуфриенко Валерий Васильевич (RU),
Напольский Виктор Петрович (RU),
Кучевский Семён Викторович (RU)
(73) Патентообладатель(и):
Захарин Александр Викторович (RU),
Шепеть Игорь Петрович (RU),
Хабаров Алексей Николаевич (RU),
Демчук Анжела Анатольевна (RU),
Онуфриенко Валерий Васильевич (RU),
Напольский Виктор Петрович (RU),
Кучевский Семен Викторович (RU)
|
(54) СПОСОБ ОПРЕДЕЛЕНИЯ ИНСТРУМЕНТАЛЬНЫХ ПОГРЕШНОСТЕЙ ИЗМЕРИТЕЛЕЙ ИНЕРЦИАЛЬНОЙ НАВИГАЦИОННОЙ СИСТЕМЫ НА ЭТАПЕ НАЧАЛЬНОЙ ВЫСТАВКИ
(57) Реферат:
Изобретение относится к измерительной технике и может быть использовано в процессе поверки бортовых навигационных систем.
Технический результат – повышение точности начальной выставки инерциальной навигационной системы. Для достижения данного результата инерциальную курсовертикаль с жестко размещенными на ней гироскопическими измерителями угловой скорости и акселерометрами принудительно вращают относительно трех осей без использования гироскопической стабилизации. Затем определяют значения идеальных выходных сигналов гироскопов и акселерометров и сравнивают с выходными сигналами гироскопов и акселерометров, снятыми с измерителей в процессе начальной подготовки инерциальной навигационной системы.
Изобретение относится к навигации и предназначено, в частности, для определения погрешностей гироскопов и акселерометров инерциальных навигационных систем на этапе начальной подготовки.
Наиболее близким к заявляемому способу по технической сущности и достигаемому эффекту является способ калибровки инструментальных погрешностей гироскопических измерителей угловой скорости инерциальной навигационной системы, в котором из выходных сигналов гироскопов, датчиков акселерометров и углов формируют сигналы, пропорциональные позиционной и интегральной составляющей горизонтальных компонент кажущегося ускорения и гироскопического курса для построения контура калибровки [1].
Недостатком данного способа является невозможность определения мультипликативных составляющих погрешностей гироскопов и акселерометров, что снижает точность определения погрешностей начальной выставки инерциальной навигационной системы.
Технической задачей изобретения является повышение точности определения погрешностей гироскопов и акселерометров за счет применения расширенной модели погрешностей гироскопов и принудительного вращения курсовертикали относительно трех осей.
Решение технической задачи или сущность изобретения заключается в том, что в способе определения инструментальных погрешностей инерциальной навигационной системы на этапе начальной выставки производят принудительное вращение инерциальной курсовертикали с жестко закрепленными на ней гироскопическими измерителями угловой скорости и акселерометрами относительно трех строительных осей объекта без использования гироскопической стабилизации, затем рассчитывают значения идеальных выходных сигналов гироскопов и акселерометров и сравнивают с выходными сигналами гироскопов и акселерометров, снятыми с измерителей в процессе начальной подготовки инерциальной навигационной системы, и определяют для гироскопов: дрейф гироскопов, ошибки масштабных коэффициентов, ошибки асимметрии масштабных коэффициентов и перекосы осей чувствительности гироскопов; для акселерометров: погрешности акселерометров, ошибки масштабных коэффициентов, ошибки асимметрии масштабных коэффициентов, ошибки отклонения центра масс акселерометров от начала координат, связанной с блоком чувствительных элементов системы координат, перекосы осей чувствительности акселерометров, используя следующую математическую модель калибровки:
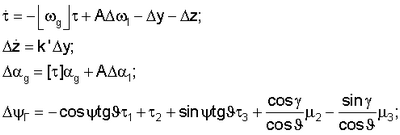
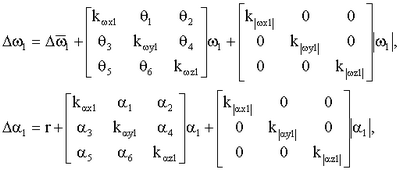
где  =[ =[ 1 1 2 2 3]T – ошибки вычисления углов ориентации; 3]T – ошибки вычисления углов ориентации;
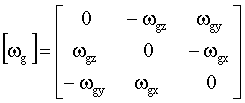 – кососимметрическая матрица, составленная из проекций угловой скорости вращения Земли на оси нормальной земной системы координат; – кососимметрическая матрица, составленная из проекций угловой скорости вращения Земли на оси нормальной земной системы координат;
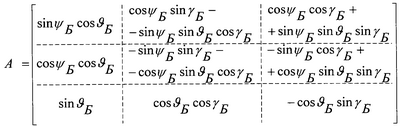 – матрица направляющих косинусов пересчета из нормальной земной системы координат в систему координат, связанную с осями чувствительности гироскопов; – матрица направляющих косинусов пересчета из нормальной земной системы координат в систему координат, связанную с осями чувствительности гироскопов;
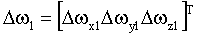 – вектор погрешностей гироскопов; – вектор погрешностей гироскопов;
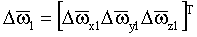 – вектор дрейфов гироскопов; – вектор дрейфов гироскопов;
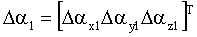 – вектор погрешностей акселерометров; – вектор погрешностей акселерометров;
 1, 1,  2, 2,  3, 3,  4, 4,  5, 5,  6 – перекосы осей чувствительности акселерометров; 6 – перекосы осей чувствительности акселерометров;
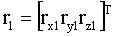 – вектор отклонения центра масс акселерометров от начала системы координат, связанной с БЧЭ; – вектор отклонения центра масс акселерометров от начала системы координат, связанной с БЧЭ;
 1, 1,  2, 2,  3, 3,  4, 4,  5, 5,  6 – перекосы осей чувствительности гироскопов; 6 – перекосы осей чувствительности гироскопов;
k x1, k x1, k y1, k y1, k z1 – ошибки масштабных коэффициентов гироскопов; z1 – ошибки масштабных коэффициентов гироскопов;
k x1, k x1, k y1, k y1, k z1 – ошибки масштабных коэффициентов акселерометров; z1 – ошибки масштабных коэффициентов акселерометров;
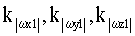 – ошибки асимметрии масштабных коэффициентов гироскопов; – ошибки асимметрии масштабных коэффициентов гироскопов;
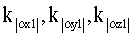 – ошибки асимметрии масштабных коэффициентов акселерометров; – ошибки асимметрии масштабных коэффициентов акселерометров;
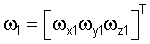 – вектор абсолютной угловой скорости вращения курсовертикали; – вектор абсолютной угловой скорости вращения курсовертикали;
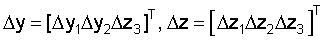 – векторы ошибок корректирующих сигналов, – векторы ошибок корректирующих сигналов, 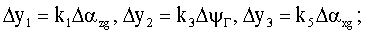
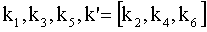 – коэффициенты обратной связи; – коэффициенты обратной связи;
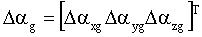 – вектор ошибок вычисления ускорения в нормальной земной системе координат; – вектор ошибок вычисления ускорения в нормальной земной системе координат;
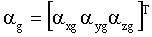 – вектор ускорений в нормальной земной системе координат; – вектор ускорений в нормальной земной системе координат;
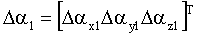 – вектор погрешностей акселерометров; – вектор погрешностей акселерометров;
  Г – ошибка вычисления гироскопического курса; Г – ошибка вычисления гироскопического курса;
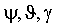 – углы курса, тангажа и крена; – углы курса, тангажа и крена;
 2, 2,  3 – погрешности датчиков углов. 3 – погрешности датчиков углов.
Сравнивают
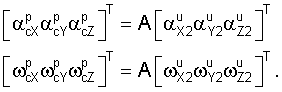
Наличие новых действий в способе определения инструментальных погрешностей измерителей инерциальной навигационной системы позволяет повысить точность начальной выставки с сохранением полной автономности указанного процесса за счет совокупности существенных отличительных признаков:
1) использования принудительного вращения инерциальной курсовертикали относительно трех строительных осей без использования гироскопической стабилизации;
2) использования математических моделей погрешностей гироскопов и акселерометров, учитывающих ошибки масштабных коэффициентов, ошибки асимметрии масштабных коэффициентов, перекосы осей чувствительности, отклонение центра масс акселерометров от начала системы координат, связанной с БЧЭ, при объединении их в блок;
3) использование сравнения снятых с измерителей значений абсолютного ускорения и угловой скорости с рассчитанными (идеальными) значениями для использования определяемых погрешностей инерциальной навигационной системы в качестве входной информации для алгоритмов оценивания.
Сравнение предложенного технического решения с его прототипом позволило установить соответствие его критерию “новизна”. При изучении других технических решений в данной области техники признаки, отличающие заявляемое изобретение от прототипа, не были выявлены и поэтому они обеспечивают заявленному техническому решению соответствие критерию “изобретательский уровень”.
Предложенное техническое решение может быть использовано в науке и технике, что обеспечивает соответствие его критерию “промышленная применимость”.
Способ реализуется следующим образом.
Известно [2], что для вычисления параметров ориентации курсовертикали относительно нормальной земной системы координат используется обобщенное уравнение Пуассона:

где Ас – матрица направляющих косинусов перехода из связанной с БЧЭ системы координат (MX2Y2Z2) в стартовую систему координат (MXcYcZc);
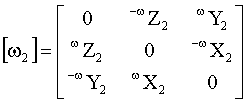 – кососимметрическая матрица, составленная из проекций абсолютной угловой скорости системы координат MX2Y2Z2, связанной с БЧЭ, на собственные оси (показания гироскопов); – кососимметрическая матрица, составленная из проекций абсолютной угловой скорости системы координат MX2Y2Z2, связанной с БЧЭ, на собственные оси (показания гироскопов);
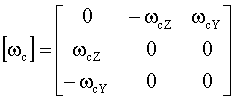 – кососимметрическая матрица, составленная из проекций абсолютной угловой скорости стартового трехгранника MXcYcZc, на собственные оси. – кососимметрическая матрица, составленная из проекций абсолютной угловой скорости стартового трехгранника MXcYcZc, на собственные оси.
Элементы кососимметрической матрицы [ с] вычисляются по информации о широте с] вычисляются по информации о широте  с места старта ЛА на основании соотношений с места старта ЛА на основании соотношений
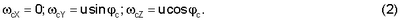
Так как ЛА на этапе начальной выставки неподвижен относительно Земли, т.е. VcX, VcY, VcZ равны нулю, то
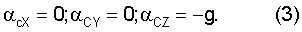
Действительно, если матрица направляющих косинусов АC, вычисленная на основании соотношения (1), отличается от истинной АСИ, то проекции ускорения на оси стартовой системы координат, вычисленные на основании соотношения
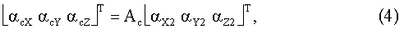
не будут совпадать с действительными значениями, представленными в (3). Разность вычисленных и действительных значений ускорений является входной для алгоритмов Калмановской фильтрации. На основании данной информации вычисляются параметры, характеризующие ориентацию БЧЭ по вертикали, а также погрешности чувствительных элементов управляемой ИНС.
Проекции угловой скорости вращения Земли на оси стартовой системы координат определяются на основании соотношений (2). Проекции показаний гироскопов на оси стартовой системы координат, вычисленные на основании соотношения
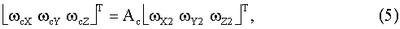
являются дополнительной информацией для определения курса БЧЭ.
Для получения математической модели ошибок ИНС на этапе начальной выставки проварьируем выражения (1):
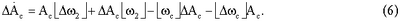
Преобразуем данное соотношение на основании понятия аналитической платформы. На этапе начальной выставки под аналитической платформой понимается система координат, отклоненная от стартовой системы координат на малые углы Эйлера-Крылова  C1, C1,  C2, C2,  C2. Несовпадение стартовой системы координат и системы координат аналитической платформы обуславливает матрицу ошибок C2. Несовпадение стартовой системы координат и системы координат аналитической платформы обуславливает матрицу ошибок

где АП – матрица направляющих косинусов перехода из связанной с БЧЭ системы координат в стартовую систему координат.
Если система координат аналитической платформы отклонена от навигационной системы координат на углы  C1, C1,  C2, C2,  C2, тогда матрица направляющих косинусов перехода от стартовой системы координат к системе координат аналитической платформы имеет вид C2, тогда матрица направляющих косинусов перехода от стартовой системы координат к системе координат аналитической платформы имеет вид 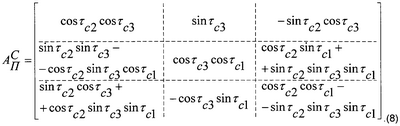
При малых значениях ошибок ориентации  C1, C1,  C2, C2,  C2 можно принять C2 можно принять
sin  ci=1; cos ci=1; cos  ci=0, где i=0…1. Если учесть только величины первого порядка малости, получим ci=0, где i=0…1. Если учесть только величины первого порядка малости, получим
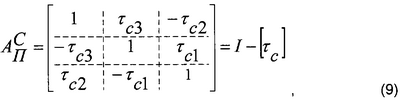
где I – единичная матрица;
[ c] – кососимметрическая матрица ошибок ориентации, соответствующая вектору-углу c] – кососимметрическая матрица ошибок ориентации, соответствующая вектору-углу  с=[ с=[ C1, C1,  С2, С2,  С2]T. С2]T.
Представим входящую в уравнение (7) матрицу АП в виде
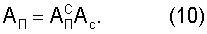
Подставляя выражения (9), (10) в уравнения (7), получим

Подставив данное выражение в уравнение (6), после преобразований получим
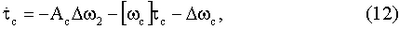
где   2 – вектор погрешностей гироскопов; 2 – вектор погрешностей гироскопов;
  c – ошибки в вычислении абсолютной угловой скорости стартовой системы координат. c – ошибки в вычислении абсолютной угловой скорости стартовой системы координат.
Значение   c получается путем варьирования уравнений (2). Ошибки в вычислении абсолютной угловой скорости навигационной системы координат на основании данных соотношений имеют вид c получается путем варьирования уравнений (2). Ошибки в вычислении абсолютной угловой скорости навигационной системы координат на основании данных соотношений имеют вид
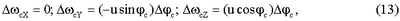
где   C – ошибка определения широты стартовой системы координат. C – ошибка определения широты стартовой системы координат.
Как было отмечено ранее, в качестве наблюдений на этапе начальной выставки используются показания акселерометров и гироскопов. Составим математическую модель наблюдений с учетом погрешностей чувствительных элементов.
Значения проекций ускорения ЛА по осям чувствительности акселерометров определяются следующим соотношением:
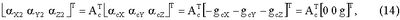
где gсх, qcy, gcz – составляющие проекций силы тяжести на оси стартовой системы координат.
Таким образом, по показаниям акселерометров можно определить проекции ускорения на оси стартовой системы координат. Однако показания акселерометров, установленных по осям связанной с БЧЭ системы координат, отличаются от величин (14) из-за ошибок акселерометров:
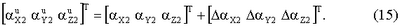
Кроме того, при реальных расчетах вместо матрицы направляющих косинусов Ас используется матрица Ап:
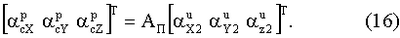
С учетом (7) данное соотношение примет вид
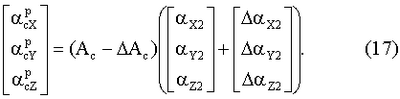
Разность истинных значений проекций ускорения на оси стартовой системы координат и рассчитанных на основании соотношения (16) является наблюдением при начальной выставке управляемой ИНС по вертикали.
Значения проекций абсолютной угловой скорости по осям чувствительности гироскопов определяется следующим соотношением:
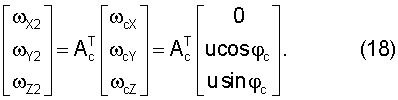
Однако показания гироскопов, установленных по осям связанной с БЧЭ системы координат, отличается от величин (18) из-за ошибок:
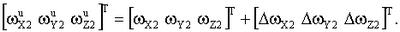
Кроме того, при реальных расчетах значение матрицы направляющих косинусов Ас неизвестно и вместо нее используется матрица Ап:
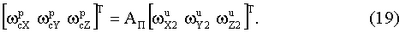
С учетом (7) данное соотношение примет вид
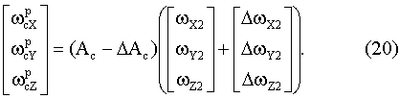
Разность истинных значений проекций угловой скорости на оси стартовой системы координат и рассчитанных на основании соотношения (19) является наблюдением при начальной выставке управляемой ИНС по курсу.
С помощью математической модели калибровки, описываемой выражениями (11), (12), (13), (16) и (17), можно построить оптимальный фильтр Калмана, который будет оценивать составляющие погрешностей гироскопов и акселерометров 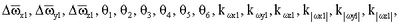 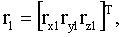 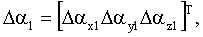  1, 1,  2, 2,  3, 3,  4, 4,  5, 5,  6, k 6, k x1, k x1, k y1, k y1, k z1, z1, 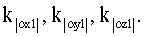
Для обеспечения наблюдаемости всех составляющих погрешностей гироскопических измерителей угловой скорости оптимальным фильтром в качестве наблюдений необходимо выбрать ошибки корректирующих сигналов  z1, z1,  z2, z2,  z3. z3.
Источники информации
1. Заявка РФ на изобретение №99111602 от 10.06.99 г., кл. G01С 21/00 (прототип).
2. Бромберг П.В. Теория инерциальных систем навигации. – М.: Наука, 1979. – 296 с.
3. Иванов М.Н., Лебеденко О.С., Сельвесюк Н.И., Шепеть И.П. Математическая модель возмущений инерциальной навигационной системы с автокомпенсацией погрешностей. М.: ЦВНИИ МО РФ, 1997. – Деп. В ЦСИФ МО РФ. Сер. Б. Вып.№40, инв. В3307. – 11 с.
Формула изобретения
Способ определения инструментальных погрешностей измерителей инерциальной навигационной системы на этапе начальной выставки, включающий измерение выходных сигналов гироскопов, акселерометров и датчиков углов пространственного положения курсовертикали относительно объекта, формирование сигналов, пропорциональных позиционной и интегральной составляющим горизонтальных компонент кажущегося ускорения и гироскопического курса для построения контура калибровки, отличающийся тем, что инерциальную курсовертикаль с жестко закрепленными на ней гироскопическими измерителями угловой скорости и акселерометрами принудительно вращают относительно трех строительных осей объекта без использования гироскопической стабилизации, затем рассчитывают значения идеальных выходных сигналов гироскопов и акселерометров и сравнивают с выходными сигналами гироскопов и акселерометров, снятыми с измерителей в процессе начальной подготовки инерциальной навигационной системы, и определяют для гироскопов: дрейф гироскопов, ошибки масштабных коэффициентов, ошибки асимметрии масштабных коэффициентов и перекосы осей чувствительности гироскопов; для акселерометров: погрешности акселерометров, ошибки масштабных коэффициентов, ошибки асимметрии масштабных коэффициентов, ошибки отклонения центра масс акселерометров от начала координат связанной с блоком чувствительных элементов системы координат, перекосы осей чувствительности акселерометров, используя следующую математическую модель калибровки:
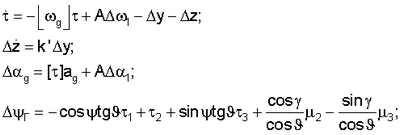
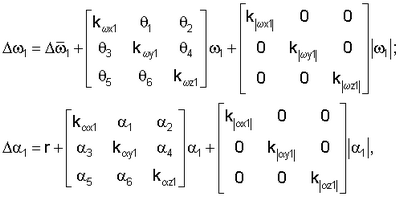
где  =[ =[ 1 1 2 2 3]T – ошибки вычисления углов ориентации; 3]T – ошибки вычисления углов ориентации;
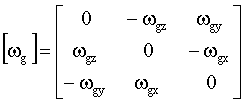 – кососимметрическая матрица, составленная из проекций угловой скорости вращения Земли на оси нормальной земной системы координат; – кососимметрическая матрица, составленная из проекций угловой скорости вращения Земли на оси нормальной земной системы координат;
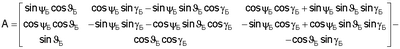
матрица направляющих косинусов пересчета из нормальной земной системы координат в систему координат, связанную с осями чувствительности гироскопов;
 – вектор погрешностей гироскопов; – вектор погрешностей гироскопов;
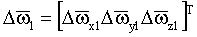 – вектор дрейфов гироскопов; – вектор дрейфов гироскопов;
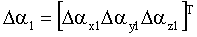 – вектор погрешностей акселерометров; – вектор погрешностей акселерометров;
 1, 1,  2, 2,  3, 3,  4, 4,  5, 5,  6 – перекосы осей чувствительности акселерометров; 6 – перекосы осей чувствительности акселерометров;
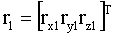 – вектор отклонения центра масс акселерометров от начала системы координат, связанной с БЧЭ; – вектор отклонения центра масс акселерометров от начала системы координат, связанной с БЧЭ;
 1, 1,  2, 2,  3, 3,  4, 4,  5, 5,  6 – перекосы осей чувствительности гироскопов; 6 – перекосы осей чувствительности гироскопов;
k x1, k x1, k y1, k y1, k z1 – ошибки масштабных коэффициентов гироскопов; z1 – ошибки масштабных коэффициентов гироскопов;
k x1, k x1, k y1, k y1, k z1 – ошибки масштабных коэффициентов акселерометров; z1 – ошибки масштабных коэффициентов акселерометров;
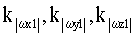 – ошибки асимметрии масштабных коэффициентов гироскопов; – ошибки асимметрии масштабных коэффициентов гироскопов;
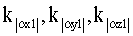 – ошибки асимметрии масштабных коэффициентов акселерометров; – ошибки асимметрии масштабных коэффициентов акселерометров;
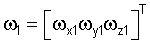 – вектор абсолютной угловой скорости вращения курсовертикали; – вектор абсолютной угловой скорости вращения курсовертикали;
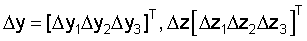 – векторы ошибок корректирующих сигналов, – векторы ошибок корректирующих сигналов, 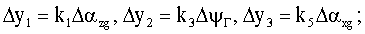
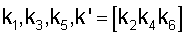 – коэффициенты обратной связи; – коэффициенты обратной связи;
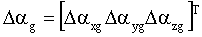 – вектор ошибок вычисления ускорения в нормальной земной системе координат; – вектор ошибок вычисления ускорения в нормальной земной системе координат;
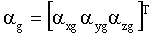 – вектор ускорений в нормальной земной системе координат; – вектор ускорений в нормальной земной системе координат;
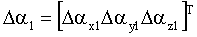 – вектор погрешностей акселерометров; – вектор погрешностей акселерометров;
  Г – ошибка вычисления гироскопического курса; Г – ошибка вычисления гироскопического курса;
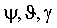 – углы курса, тангажа и крена; – углы курса, тангажа и крена;
 2, 2,  3 – погрешности датчиков углов, 3 – погрешности датчиков углов,
сравнивают
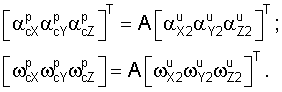
|