|
(21), (22) Заявка: 2005132811/28, 24.10.2005
(24) Дата начала отсчета срока действия патента:
24.10.2005
(46) Опубликовано: 20.04.2007
(56) Список документов, цитированных в отчете о
поиске:
SU 953502 A1, 23.08.1982. RU 2110069 C1, 27.04.1998. RU 2169355 C1, 20.06.2001. SU 1497491 A1, 30.07.1989. WO 2004038384, 06.05.2004. JP 8233713, 13.09.1996.
Адрес для переписки:
426067, г.Ижевск, ул. Татьяны Барамзиной, 34, Институт прикладной механики УрО РАН
|
(72) Автор(ы):
Вахрушев Александр Васильевич (RU),
Шушков Андрей Александрович (RU)
(73) Патентообладатель(и):
Институт прикладной механики УрО РАН (RU)
|
(54) СПОСОБ ОПРЕДЕЛЕНИЯ МОДУЛЯ УПРУГОСТИ ЮНГА И КОЭФФИЦИЕНТА ПУАССОНА МАТЕРИАЛА МИКРО- И НАНОЧАСТИЦ
(57) Реферат:
Изобретение относится к способам определения модуля упругости Юнга материалов, а именно сферических микро- и наночастиц, входящих в состав композиционного материала. Техническим результатом изобретения является возможность определения модуля упругости и коэффициента Пуассона для монодисперсных сферических микро- и наночастиц. Способ определения модуля упругости основан на том, что изготавливают образец из полимерной матрицы с добавлением заданного процентного содержания (1-7)% монодисперсных сферических микро- или наночастиц. Проводят экспериментальное одноосное сжатие образца композиционного материала. Определяют продольные и поперечные деформации образца. Строят зависимость продольных деформаций от осевого напряжения. По линейному участку кривой деформирования определяют модуль упругости и коэффициент Пуассона композиционного материала, и на основании полученных значений модуля упругости и коэффициента Пуассона композиционного материала определяют модуль упругости и коэффициент Пуассона для монодисперсных сферических микро- и наночастиц. 3 з.п. ф-лы, 2 ил.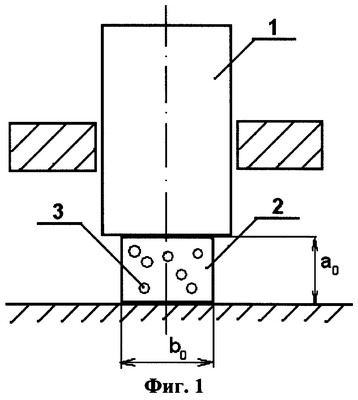
Изобретение относится к способам определения механических свойств материалов путем приложения растягивающих или сжимающих нагрузок, а именно к способам определения модуля упругости Юнга и коэффициента Пуассона.
Известен способ определения модуля упругости [Регистрационный номер заявки № 96116367/03, кл. G01N 33/38, 1998], основанный на том, что изготавливают образцы, содержащие эталонный и исследуемый крупный заполнитель с различной его абсолютной концентрацией. Модуль упругости растворной составляющей определяют по результатам испытаний бетонных образцов на эталонном заполнителе, а модуль упругости исследуемого заполнителя находят из формулы.
Недостатком указанного способа определения модуля упругости является его неприменимость к образцам композиционных материалов, содержащих монодисперсные сферические микро- или наночастицы.
nt по формуле (1):
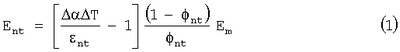



где  0 и 0 и  q – частоты связи до и после охлаждения; q – частоты связи до и после охлаждения;  nt и nt и  m – коэффициенты теплового расширения нанотрубки и матрицы; T0 и Тq – температура до охлаждения и после; m – коэффициенты теплового расширения нанотрубки и матрицы; T0 и Тq – температура до охлаждения и после;  nt – доля объема углеродных нанотрубок или углеродных волокон в составе образца; Еm – модуль упругости матрицы; nt – доля объема углеродных нанотрубок или углеродных волокон в составе образца; Еm – модуль упругости матрицы;  nt – деформация длины связи. nt – деформация длины связи.
Недостатком указанного способа определения модуля упругости является то, что он непригоден для определения коэффициента Пуассона включений, добавленных в эпоксидную матрицу.
Задача изобретения – получение способа определения модуля упругости и коэффициента Пуассона сферических микро- и наночастиц на основе приложения осевых нагрузок к образцу композиционного материала.
Способ определения модуля упругости включает в себя два этапа.
1. Изготавливают образец из полимерной матрицы с добавлением заданного процентного содержания (1-7)% монодисперсных сферических микро- или наночастиц. Процентное содержание микро- или наночастиц в образце материала выбирается исходя из того, что частицы так малы и настолько удалены одна от другой, что взаимодействием между ними можно пренебречь. Сферические частицы равномерно распределены в образце композиционного материала. Размер всех частиц, входящих в состав образца, должен быть одинаков. Проводят экспериментальное одноосное сжатие образца композиционного материала силой n*F, где n=1,9…m.
Определяют продольные и поперечные деформации образца. Строят зависимость продольной деформации от осевого напряжения.
2. Определяют по линейному участку кривой деформирования модуль упругости и коэффициент Пуассона композиционного материала. Вычисляют значения модуля упругости и коэффициента Пуассона материала сферических микро- или наночастиц.
На фиг.1 представлена конструкция для реализации предлагаемого способа.
На фиг.2 представлена схема сжатия пуансоном 1 композиционного материала 2 с упругими сферическими включениями 3 после приложения силы F.
Способ реализуется следующим образом: с помощью пуансона 1 прикладывают силу n*F при n=1, действующую на композиционный материал 2, содержащий сферические включения 3, представляющие собой монодисперсные шарообразные микро- или наночастицы.
Определяют продольную  пр1 и поперечную пр1 и поперечную  поп1 деформацию (5, 6), осевое напряжение (7) поп1 деформацию (5, 6), осевое напряжение (7)


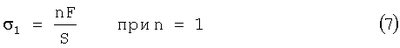
где S – площадь сечения перпендикулярного оси образца композиционного материала.
Продолжают прикладывать силы n*F, где n=2, …m, находят продольные, поперечные деформации и осевые напряжения. Строят зависимость продольной деформации от осевого напряжения. Для линейного участка кривой деформирования определяют модуль упругости Е (8) и коэффициент Пуассона  (9) композиционного материала (9) композиционного материала
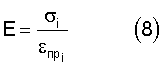
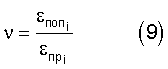
где i – точка на линейном участке кривой деформирования.
Вычисляют модуль сдвига  (10) и объемный модуль k (11) композиционного материала (10) и объемный модуль k (11) композиционного материала


По формулам (12), (13) вычисляют модуль сдвига  I и объемный модуль kI сферических микро- или наночастиц [Р.Кристенсен, Введение в механику композитов: Издательство МИР, 1982, с.50-51] I и объемный модуль kI сферических микро- или наночастиц [Р.Кристенсен, Введение в механику композитов: Издательство МИР, 1982, с.50-51]
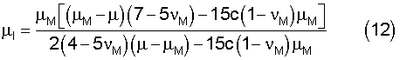
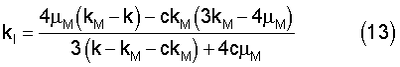
где  M, kM, M, kM,  M – модуль сдвига, объемный модуль и коэффициент Пуассона полимерной матрицы, с – концентрация (14) M – модуль сдвига, объемный модуль и коэффициент Пуассона полимерной матрицы, с – концентрация (14)

VI – объем монодисперсных сферических микро- или наночастиц, V – объем образца композиционного материала.
Определяют модуль упругости EI (15) и коэффициент Пуассона  I (16) сферических микро- или наночастиц I (16) сферических микро- или наночастиц
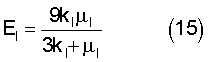
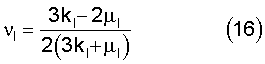
Благодаря предложенному способу стало возможным определять модуль упругости и коэффициент Пуассона для монодисперсных сферических микро- и наночастиц.
Формула изобретения
1. Способ определения модуля упругости Юнга композиционных материалов путем приложения растягивающих или сжимающих нагрузок, отличающийся тем, что изготавливают образец из полимерной матрицы с добавлением заданного процентного содержания монодисперсных сферических микро- или наночастиц, проводят экспериментальное одноосное сжатие образца композиционного материала, определяют продольную и поперечную деформацию образца, строят зависимость продольной деформации от осевого напряжения, определяют по линейному участку кривой деформирования модуль упругости и коэффициент Пуассона композиционного материала; на основе полученных значений модуля упругости и коэффициента Пуассона образца вычисляют значения модуля упругости и коэффициента Пуассона материала микро- или наночастиц.
2. Способ по п.1, отличающийся тем, что процентное содержание монодисперсных сферических микро- или наночастиц в образце композиционного материала составляет 1-7%.
3. Способ по п.1, отличающийся тем, что монодисперсные сферические микро- или наночастицы в образце композиционного материала имеют одинаковый размер.
4. Способ по п.1, отличающийся тем, что монодисперсные сферические микро- или наночастицы равномерно распределены в образце композиционного материала.
РИСУНКИ
MM4A – Досрочное прекращение действия патента СССР или патента Российской Федерации на изобретение из-за неуплаты в установленный срок пошлины за поддержание патента в силе
Дата прекращения действия патента: 25.10.2007
Извещение опубликовано: 27.06.2009 БИ: 18/2009
|