Патент на изобретение №2296972

(54) СПОСОБ ОПРЕДЕЛЕНИЯ МОДУЛЯ УПРУГОСТИ ЮНГА МАТЕРИАЛОВ

(57) Реферат:

Изобретение относится к способам определения механических свойств материалов. Сущность: проводят экспериментальные сжатия шарообразной микро- или наночастицы разной сосредоточенной силой. Вычисляют перемещения в точке действия силы на частицу. Строят зависимость перемещений от величины прикладываемой силы в точке действия силы на частицу. Для справочных значений модуля упругости и коэффициента Пуассона исследуемого материала сравнивают экспериментальную зависимость перемещений от величины прикладываемой силы в точке ее действия на частицу с аналитической зависимостью перемещений от величины прикладываемой силы в точке действия силы на упругий шар, сжимаемый сосредоточенными силами, приложенными в противоположные концы диаметра и направленными параллельно. Радиус упругого шара равен радиусу частицы, прикладываемые расчетные силы к упругому шару равны прикладываемой силе к частице. Изменяя модуль упругости, находят такое его значение, при котором совпадают (из расчета минимальной среднеквадратичной ошибки) экспериментальная зависимость перемещений от величины прикладываемой силы в точке действия силы на частицу с аналитической зависимостью перемещений от величины прикладываемой силы в точке действия силы на упругий шар, сжимаемый сосредоточенными силами, приложенными в противоположные концы его диаметра. Технический результат: возможность определения модуля упругости для шарообразных микро- и наночастиц. 4 ил.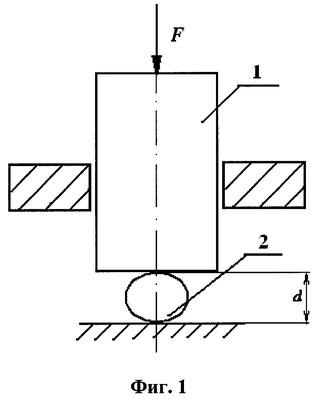

Изобретение относится к способам определения механических свойств материалов путем приложения растягивающих или сжимающих нагрузок, а именно к способам определения статического модуля упругости Юнга (ниже модуль упругости).

Известен способ определения модуля упругости [Авторское свидетельство СССР №954850, кл. G 01 N 3/08, 1982], основанный на том, что нагружают растяжением образец материала, имеющий площадь F сечения, с установленным на нем датчиком деформации, измеряют сигнал R с датчика, соответствующий изменению напряжения в рабочем сечении. Используют образец эталонного материала, имеющий площадь F_Э сечения и модуль упругости Е_Э, с установленным на нем датчиком деформации, который размещают последовательно с образцом исследуемого материала и нагружают одновременно с ним, измеряют сигнал R_Э с датчика, установленного на образце эталонного материала, и рассчитывают модуль упругости Е материала.

Недостатками указанного способа определения модуля упругости являются: невозможность его применения к образцам материалов с непостоянной площадью сечения, например шарообразным образцам, а также необходимость использования эталонного материала.

Наиболее близким к заявляемому техническому решению, принятым за прототип, является способ определения модуля упругости, основанный на том, что в материал внедряют цилиндрический индентор без сцепления его с материалом и измеряют глубину внедрения, затем внедряют индентор с сцеплением с материалом при той же нагрузке. Определяют отношение глубин внедрения, по которым судят о модуле упругости [Авторское свидетельство СССР №957054, кл. G 01 N 3/42, 1982].

Недостатком указанного способа определения модуля упругости является сложность его реализации в образцах материалов малых размеров, меньших 100 нм.

Задача изобретения – устранение указанных недостатков, а именно получение способа определения модуля упругости для шарообразных микро- и наночастиц.

Данная задача решается с помощью экспериментального сжатия шарообразной частицы сосредоточенной силой n·F, где n=1,…k и может принимать не только целочисленные значения. После приложения силы n·F при n=1 вычисляют перемещение в точке действия силы на частицу. Затем к исходной частице прикладывают силу при n>1 и так далее. Таким образом, происходит сжатие частицы разными силами. Параметр k выбирают исходя из того, чтобы прикладываемая сила являлась сосредоточенной. При слишком большом значении k в ходе экспериментального сжатия это условие не выполняется. Строят зависимость перемещений от величины прикладываемой силы в точке действия силы на частицу. Строят аналитическую зависимость перемещений от величины прикладываемой силы в точке действия силы для упругого шара, сжимаемого сосредоточенными силами, приложенными в противоположные концы диаметра и направленными параллельно. Для справочных значений модуля упругости и коэффициента Пуассона исследуемого материала сравнивают экспериментальную зависимость перемещений от величины прикладываемой силы в точке ее действия на частицу с аналитической зависимостью перемещений от величины прикладываемой силы в точке действия силы на упругий шар, сжимаемый сосредоточенными силами, приложенными в противоположные концы диаметра и направленными параллельно. При этом радиус упругого шара равен радиусу частицы, прикладываемые расчетные силы к упругому шару равны прикладываемой силе к частице. Изменяя модуль упругости, находят такое его значение для справочного значения коэффициента Пуассона, при котором совпадают (из расчета минимальной среднеквадратичной ошибки) экспериментальная зависимость перемещений от величины прикладываемой силы в точке действия силы на частицу с аналитической зависимостью перемещений от величины прикладываемой силы в точке действия силы на упругий шар, сжимаемый сосредоточенными силами, приложенными в противоположные концы его диаметра.

На фиг.1 представлена схема сжатия шарообразной наночастицы после приложения сосредоточенной силы.

На фиг.2 представлен упругий шар, сжимаемый сосредоточенными силами F, приложенными в противоположные концы его диаметра d₀.

На фиг.3 представлена аналитическая зависимость перемещений от величины прикладываемой силы в точке ее действия на упругий шар (1), сжимаемый сосредоточенными силами, приложенными в противоположные концы его диаметра, для Е=9.5·10¹⁰ Па, =0.21 и экспериментальная зависимость перемещений (2) от величины прикладываемой силы к наночастице с числом атомов 216 в точке действия силы.

На фиг.4 представлена аналитическая зависимость перемещений от величины прикладываемой силы в точке ее действия на упругий шар (1), сжимаемый сосредоточенными силами, приложенными в противоположные концы его диаметра, для Е=17.1·10¹⁰ Па, =0.21 и экспериментальная зависимость перемещений (2) от величины прикладываемой силы к наночастице с числом атомов 216 в точке действия силы.

Способ реализуется следующим образом: с помощью пуансона 1 прикладывают силу n·F, где n=1, действующую на частицу 2. Вычисляют перемещение в точке действия силы на частицу по формуле 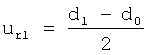, где d₀ – начальный диаметр частицы, d₁ – диаметр частицы после сжатия силой n·F при n=1. Исследуемым материалом в описании примера применения способа является цинк. Для наночастицы цинка, состоящей из N=216 атомов, F=6.955·10^-12 H, d₀=11.997·10^-10 м, d₁=11.979·10^-10 м, соответственно u_r1=-1.8·10^-12 м. После вычисления перемещения u_r1 к исходной наночастице прикладывают силу n·F для n=2, находят перемещение u_r2. Продолжают прикладывать силы и находить соответствующие перемещения для n7. Справочные значения модуля упругости и коэффициента Пуассона для цинка равны E=9.5·10¹⁰ Па, =0.21. Строят зависимость перемещений от величины прикладываемой силы в точке действия силы на наночастицу.

Для справочных значений модуля упругости Е и коэффициента Пуассона строят аналитическую зависимость перемещений от величины прикладываемой силы F в точке действия силы на упругий шар, сжимаемый сосредоточенными силами, приложенными в противоположные концы его диаметра d₀ и направленными параллельно по формуле (1).

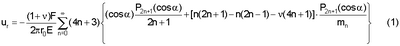
где r₀ – радиус шара, P_2n+1(cos) – полином Лежандра, m_n – функция, зависящая от и n [В.И.Блох, Теория упругости: Издательство Харьковского Университета, 1964, с.463].

Изменяя модуль упругости Е, находят такое его значение E=17.1·10^-10 Па, при котором совпадают (из расчета минимальной среднеквадратичной ошибки) экспериментальная зависимость перемещений от величины прикладываемой силы в точке действия силы на наночастицу с аналитической зависимостью перемещений от величины прикладываемой силы в точке действия силы на упругий шар, сжимаемый сосредоточенными силами, приложенными в противоположные концы его диаметра.

Благодаря предложенному способу стало возможным определять модуль упругости и в шарообразных микро- и наночастицах.

Формула изобретения

Способ определения модуля упругости Юнга материалов путем приложения сжимающих нагрузок, отличающийся тем, что проводят экспериментальные сжатия шарообразной микро или наночастицы разной сосредоточенной силой, вычисляют перемещения в точке действия силы на частицу; строят зависимость перемещений от величины прикладываемой силы в точке действия силы на частицу; для справочных значений модуля упругости и коэффициента Пуассона исследуемого материала сравнивают экспериментальную зависимость перемещений от величины прикладываемой силы в точке ее действия на частицу с аналитической зависимостью перемещений от величины прикладываемой силы в точке действия силы на упругий шар, сжимаемый сосредоточенными силами, приложенными в противоположные концы диаметра и направленными параллельно, при этом радиус упругого шара равен радиусу частицы, прикладываемые расчетные силы к упругому шару равны прикладываемой силе к частице; изменяя модуль упругости, находят такое его значение, при котором совпадают (из расчета минимальной среднеквадратичной ошибки) экспериментальная зависимость перемещений от величины прикладываемой силы в точке действия силы на частицу с аналитической зависимостью перемещений от величины прикладываемой силы в точке действия силы на упругий шар, сжимаемый сосредоточенными силами, приложенными в противоположные концы его диаметра.

РИСУНКИ

MM4A – Досрочное прекращение действия патента СССР или патента Российской Федерации на изобретение из-за неуплаты в установленный срок пошлины за поддержание патента в силе

Дата прекращения действия патента: 30.07.2007

Извещение опубликовано: 10.03.2009 БИ: 07/2009