|
|
(21), (22) Заявка: 2005112605/14, 26.04.2005
(24) Дата начала отсчета срока действия патента:
26.04.2005
(43) Дата публикации заявки: 10.11.2006
(46) Опубликовано: 10.03.2007
(56) Список документов, цитированных в отчете о
поиске:
КОЗЛОВ Л.Б. и др. Математическое моделирование эпидемического процесса при клещевом энцефалите. Научный вестник Тюменской медицинской академии. 2002, № 7-8, с.103. RU 2221247 С2, 10.01.2004. ЦОКОВА Т.Н. и др. Математическое моделирование эпидемического процесса при клещевом энцефалите. Успехи современного естествознания. 2003, № 11, с.91. 2002, №
Адрес для переписки:
625023, г.Тюмень, ул. Одесская, 54, ГОУ ВПО ТюмГМА Росздрава, научный отдел, патентоведу Л.Б. Козлову
|
(72) Автор(ы):
Козлов Леонид Борисович (RU),
Кашуба Эдуард Алексеевич (RU),
Цокова Татьяна Николаевна (RU),
Губин Денис Генадьевич (RU),
Мефодьев Владимир Васильевич (RU),
Огурцов Анатолий Анатольевич (RU),
Устюжанин Юрий Викторович (RU),
Соколова Галина Васильевна (RU),
Николаева Тагзима Галиевна (RU)
(73) Патентообладатель(и):
Федеральное агентство по здравоохранению и социальному развитию Государственное образовательное учреждение Высшего профессионального образования Тюменская государственная медицинская академия (ГОУ ВПО ТюмГМА Росздрава) (RU)
|
(54) СПОСОБ ПРОГНОЗА ЗАБОЛЕВАЕМОСТИ КЛЕЩЕВЫМИ ИНФЕКЦИЯМИ
(57) Реферат:
Изобретение относится к области медицины, а именно к эпидемиологии, и может быть использовано для прогноза заболеваемости клещевыми инфекциями (КИ) и планирования противоэпидемических мероприятий в природных очагах. Прогноз заболеваемости КИ осуществляют по учету заболеваемости КИ за промежутки времени, равные 5 дням, в течение временного ряда t. Определяют показатель сглаживания сезонной составляющей S(t), которая для первого года трехлетнего цикла соответствует S1(t), для второго года S2(t), для третьего года S3(t), при этом 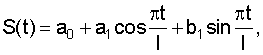 где а0=0; a1: для S1(t) соответствует -0,111, для S2(t) соответствует -0,977, а для S3(t) соответствует 0,362; b1: для S1(t) соответствует 2,155, для S2(t) соответствует 4,619, а для S3(t) соответствует -1,813; где а0=0; a1: для S1(t) соответствует -0,111, для S2(t) соответствует -0,977, а для S3(t) соответствует 0,362; b1: для S1(t) соответствует 2,155, для S2(t) соответствует 4,619, а для S3(t) соответствует -1,813;  /l: для S1(t) соответствует 6 /l: для S1(t) соответствует 6 , для S2(t) соответствует 6 , для S2(t) соответствует 6 , а для S3(t) соответствует 7,6 , а для S3(t) соответствует 7,6 , l – число периодов тригонометрических функций, которые выбирают в соответствии с числом максимумов временного ряда. Прогноз заболеваемости КИ проводят по следующим формулам, позволяющим определить прогнозируемое количество случаев заболеваний КИ за временной интервал: для первого года трехлетнего цикла Y1(t)*=-4,48+5,15t-0,41t2+0,01t3+S1(t); для второго года трехлетнего цикла Y2(t)*=-2,44+3,08t-0,5t2-0,01t3+S2(t); для третьего года трехлетнего цикла Y3(t)*=-4,43+4,82t-0,14t2-0,1t3+S3(t). Способ позволяет осуществить расчет заболеваемости КИ на каждый год трехлетнего цикла природноочаговых инфекций и в отдельный период эпидемического сезона с пятидневным интервалом. 6 ил, 6 табл. , l – число периодов тригонометрических функций, которые выбирают в соответствии с числом максимумов временного ряда. Прогноз заболеваемости КИ проводят по следующим формулам, позволяющим определить прогнозируемое количество случаев заболеваний КИ за временной интервал: для первого года трехлетнего цикла Y1(t)*=-4,48+5,15t-0,41t2+0,01t3+S1(t); для второго года трехлетнего цикла Y2(t)*=-2,44+3,08t-0,5t2-0,01t3+S2(t); для третьего года трехлетнего цикла Y3(t)*=-4,43+4,82t-0,14t2-0,1t3+S3(t). Способ позволяет осуществить расчет заболеваемости КИ на каждый год трехлетнего цикла природноочаговых инфекций и в отдельный период эпидемического сезона с пятидневным интервалом. 6 ил, 6 табл.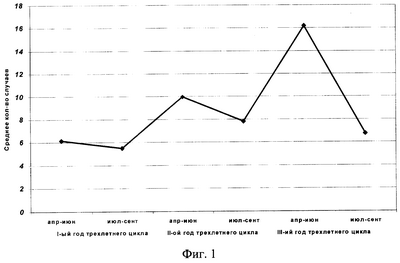
(56) (продолжение):
CLASS=”b560m”7-8, с.103. ГОЛЫЧЕВА И.В. и др. Возможности факторного прогнозирования заболеваемости клещевым энцефалитом в Приморском крае. Паразитология. 2002, т.36. № 4. с.280-285.
Изобретение относится к области медицины, а именно к эпидемиологии, и может быть использовано для прогноза заболеваемости клещевыми инфекциями (КИ) и планирования противоэпидемических мероприятий в природных очагах.
В патентной литературе описаны методы прогнозирования течения и исходов заболеваемости клещевым энцефалитом (КЭ) (патент RU №2221247 С2, опубл. 10.01.2004 г.; патент RU №2202789 С2, опубл. 20.04.2003 г.) не позволяющие определить уровень инфекционной заболеваемости КЭ в природных очагах.
Предложенный способ имеет ряд недостатков, прежде всего необходимо изучать состояние иммунитета у населения в различных возрастных группах с помощью серологических реакций и проводить сбор данных о частоте присасывания клещей в различных возрастных группах населения. Кроме того, способ нельзя использовать для определения риска заражения среди жителей городов, не имеющих иммунитета к вирусу КЭ.
Применение данного способа в условиях одного из районов Тюменской области выявило существенные недостатки, обусловленные тем, что оценка вероятности заболевания согласно принятой математической модели не учитывает ряда значимых показателей активности природного очага клещевого энцефалита, и вследствие этого способ обладает невысокой достоверностью.
Задачей настоящего изобретения является разработка нового, простого, экономичного способа прогнозирования заболеваемости КИ.
Поставленная задача решается на основании многолетнего анализа временного ряда заболеваемости КИ по материалам карт эпидемиологического обследования и составления формул прогноза заболеваемости.
Технический результат – простой, не требующий материальных затрат способ прогноза заболеваемости КИ.
Технический результат достигается тем, что способ прогноза заболеваемости клещевыми инфекциями согласно изобретению включает учет заболеваний КИ за промежутки времени, равные 5 дням, в течение временного ряда – t, определение показателя сглаживания сезонной составляющей – S(t), которая для первого года трехлетнего цикла соответствует S1(t), для второго года – S2(t), для третьего года – S3(t), при этом 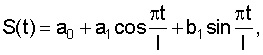 где a0=0; а1: для S1(t) соответствует -0,111, для S2(t) – -0,977, а для S3(t) – 0,362; b1: для S1(t) соответствует 2,155, для S2(t) – 4,619, а для S3(t) – -1,813; где a0=0; а1: для S1(t) соответствует -0,111, для S2(t) – -0,977, а для S3(t) – 0,362; b1: для S1(t) соответствует 2,155, для S2(t) – 4,619, а для S3(t) – -1,813; 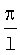 : для S1(t) соответствует 6 : для S1(t) соответствует 6 , для S2(t) – 6 , для S2(t) – 6 ; а для S3(t) – 7,6 ; а для S3(t) – 7,6 , l – число периодов тригонометрических функций, которые выбирают в соответствии с числом максимумов временного ряда; прогноз заболеваемости КИ проводят по следующим формулам, позволяющим определить прогнозируемое количество случаев заболеваний КИ за временной интервал: для первого года трехлетнего цикла Y1(t)*=-4,48+5,15t-0,41t2+0,01t3+S1(t); для второго года трехлетнего цикла Y2(t)*=-2,44+3,08t-0,5t2-0,01t3+S2(t); для третьего года трехлетнего цикла Y3(t)*=-4,43+4,82t-0,14t2-0,1t3+S3(t). , l – число периодов тригонометрических функций, которые выбирают в соответствии с числом максимумов временного ряда; прогноз заболеваемости КИ проводят по следующим формулам, позволяющим определить прогнозируемое количество случаев заболеваний КИ за временной интервал: для первого года трехлетнего цикла Y1(t)*=-4,48+5,15t-0,41t2+0,01t3+S1(t); для второго года трехлетнего цикла Y2(t)*=-2,44+3,08t-0,5t2-0,01t3+S2(t); для третьего года трехлетнего цикла Y3(t)*=-4,43+4,82t-0,14t2-0,1t3+S3(t).
Простой, экономичный способ, не требующий материальных затрат.
Заявляемый способ иллюстрируется графиками, где на фиг.1 представлена динамика трехлетнего цикла заболеваемости КЭ на юге Тюменской области за период с 1994-2002 гг.; на фиг.2 – динамика заболеваемости КЭ с пятидневным интервалом на юге Тюменской области за 1997 г.; на фиг.3 – трехлетний цикл заболеваемости КЭ на юге Тюменской области за период 1994-2002 гг. без учета случайных факторов, влияющих на заболеваемость; на фиг.4 – трехлетний цикл заболеваемости КЭ на юге Тюменской области за период 1994-2002 гг. без учета сезонной составляющей (тренд); на фиг.5 – трехлетний цикл заболеваемости КЭ на юге Тюменской области за период 1994-2002 гг. с учетом сезонной составляющей (тренд); на фиг.6 – динамика трехлетнего цикла заболеваемости иксодового клещевого боррелиоза (ИКБ) на юге Тюменской области за период 1994-2002 гг.
Предлагаемый способ осуществляют следующим образом. На модели КЭ согласно изобретению по данным карт эпидемиологического обследования больных формируют временные ряды числа заболеваний КЭ с пятидневным интервалом с 1 апреля по 30 сентября за период с 1994 по 2002 гг., составляют ежегодные временные ряды, состоящие из 36 значений, и устанавливают цикличность заболеваемости КЭ по параметрам ритмов (табл.1).
Таблица 1
Параметры ритмов заболеваемости КЭ |
| Длительность ритма |
Сутки [годы] |
Амплитуда ± se (количество заболеваний) |
Акрофаза ± se (градусы) |
Мезор ± se (количество заболеваний) |
| Окологодовой |
365 [годы] |
7,1±0,6 |
– 122±7 |
6,4±0,6 |
| Околотрехлетний |
1095 |
4,2±0,7 |
– 130±10 |
| Параметры наилучшей апроксимации для трехлетнего цикла |
1072±22 [2,94±0,06] |
4.2±0,6 |
– 226±8 |
Определяем среднее количество заболеваний за 5 дней в течение апреля-июня и июля-сентября трехгодичного цикла за 9-12 лет (фиг.1) и устанавливаем средние параметры трехлетнего цикла заболеваемости КЭ, затем для учета ежегодной заболеваемости КЭ составляем аддитивную модель:
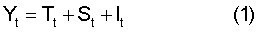
где Yt – абсолютное значение числа заболеваний в момент времени, равный 5 дням, в течение временного ряда t,
Tt – основная составляющая числа заболеваний временного ряда t (тренд),
St – сглаживание числа заболеваний в соответствии с сезонными факторами в течение временного ряда t,
It – компонент, учитывающий число заболеваний, возникающих в результате действия случайных факторов.
На фигуре 2 представлены результаты учета заболеваемости КЭ по пятидневкам за 1997 г. График имеет почти параболический тренд с устойчивым максимумом числа заболевших. Количество заболеваний ежемесячно повторяется и имеет почти один и тот же характер в каждом месячном интервале.
Для устранения компонента, обуславливающего случайный фактор, использовано сглаживание значений ряда, при котором происходило взаимное поглощение несистематических компонент (фиг.3). Первая кривая (а) соответствовала первому году трехлетнего цикла, вторая (б) – второму году трехлетнего цикла, а третья (в) – третьему году трехлетнего цикла.
Ошибку устранения случайного фактора определяли по формуле:
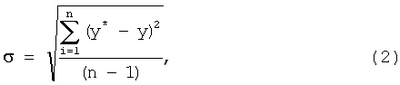
где y – значение числа заболеваний в момент времени, равный 5 дням, в течение временного ряда t (t=от 1 до 36),
y* – значение числа заболеваний за 5 дней после усреднения. Полученные значения среднеквадратического отклонения для каждого года представлены в таблице 2.
Таблица 2
Среднеквадратическое отклонение значений временного ряда от усредненных значений для каждого года |
| N |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
| годы |
1994 |
1995 |
1996 |
1997 |
1998 |
1999 |
2000 |
2001 |
2002 |
 |
0.532870 |
1.168649 |
1.383043 |
0.907785 |
1.361395 |
1.141258 |
0.438326 |
0.621751 |
1.444177 |
Средние значения ошибки для каждого года трехлетнего цикла составили: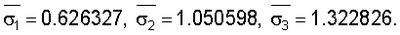
Для нахождения основной составляющей временного ряда (тренда) выбраны полиномы П.Л.Чебышева (Чебышев П.Л. / В сб. Теория вероятностей и математическая статистика”, Венецкий И.Г., Кильдишев Г.С.. – М.: Статистика, 1975. – 264 с.):
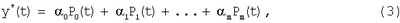
Факторный признак можно представить натуральным рядом чисел. Оказывается, как доказал П.Л.Чебышев, добавляемый член имеет вид:
am+1Pm+1(t), где Pm+1(t) определяется по общей формуле
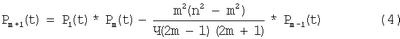
P0(t)=1
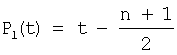
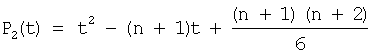
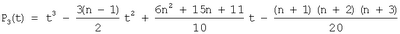
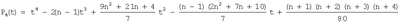
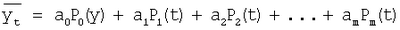
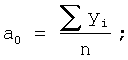
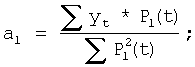
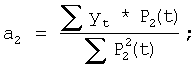
…………………………
…………………………

и т.д.
Числители параметров (5) определяются непосредственно. Знаменатели рассчитываются по следующей общей формуле 6:
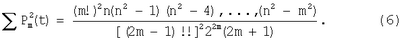
В частности, при целых значениях n расчет проводят по формулам (7).
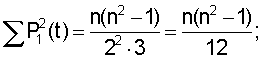
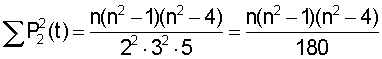
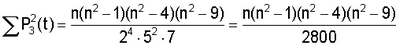
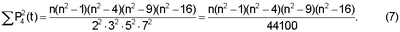
После нахождения уравнения для выравнивания вычисляют (по формуле (2).
Переход к многочленам более высокого порядка производят до тех пор, пока дисперсия продолжает уменьшаться.
где Pm+1(t) определяли по общей формуле 8:
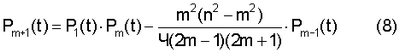
Ошибка  * установлена по формуле (2), где y* – значения, рассчитанные по полиному n-й степени. Оптимальным полиномом взяты значения, при которых * установлена по формуле (2), где y* – значения, рассчитанные по полиному n-й степени. Оптимальным полиномом взяты значения, при которых  * *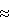  (табл.2). (табл.2).
По уравнению многочлена найдены значения полиномов. Установлены лучшие апроксимирующие полиномы для первого, второго и третьего года трехлетнего цикла заболеваемости КЭ, формулы 9:
для первого года
T1(t)*=-4,48+5,15t-0,41t2+0,01t3,  *=0,40; *=0,40;
для второго года
T2(t)*=-2,44+3,08t-0,5t2-0,01t3,  *=0,65; *=0,65;
для третьего года трехлетнего цикла
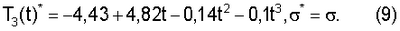
На фигуре 4 представлена основная составляющая ряда заболеваемости КЭ без учета сезонной составляющей (1) соответственно для 1-го, 2-го и 3-го года трехлетнего цикла.
Сезонная составляющая увеличивает значения временного ряда на определенную величину, поэтому используют складывание ее со значением тренда.
Сглаживание сезонной составляющей проведено отдельно, используя тригонометрическую функцию (формула 10):
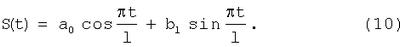
Лучшими коэффициентами a0, a1, bi считались те, при которых период функции S(t) соответствовал периоду сезонной составляющей вводимого временного ряда. Полученные значения представлены в таблице 3.
Таблица 3
Сезонные составляющие временных рядов для 1-го,2-го и 3-го годов трехлетнего цикла заболеваемости КЭ |
| |
a0 |
a1 |
B1 |
 ** ** |
 /l /l |
| S1(t) |
0 |
-0,111 |
2,155 |
4,75 |
6 |
| S2(t) |
0 |
-0,977 |
4,619 |
5,33 |
6 |
| S3(t) |
0 |
0,362 |
-1,813 |
5,89 |
7,6 |
Так как a0 – высота над горизонтальной осью, то в дальнейшем ее следует взять равной нулю во всех формулах S(t).
 ** рассчитывали по формуле (2), где y* – значение временного ряда с учетом сезонной составляющей; l – число периодов тригонометрических функций, выбранных в соответствии с числом максимумов временного ряда. ** рассчитывали по формуле (2), где y* – значение временного ряда с учетом сезонной составляющей; l – число периодов тригонометрических функций, выбранных в соответствии с числом максимумов временного ряда.
На фигуре 5 представлены графики трендов с учетом сезонной составляющей (1) для 1-го, 2-го и 3-го года трехлетнего цикла заболеваемости КЭ.
Подставив в формулу (1) значения Tt (формула 9) и St (формула 10) получим формулу прогноза на каждый год 3-х летнего цикла заболеваемости КЭ (формула II):
для первого года трехлетнего цикла
Y1(t)*=-4,48+5,15t-0,41t2+0,01t3+S1(t); Y1(t)=318, где Y1(t) суммарное значение числа заболеваний КЭ за первый год трехлетнего цикла [Y1(t)=Y1(1)+Y1(2)+Y1(3)+…+Y1(36)];
для второго года трехлетнего цикла
Y2(t)*=-2,44+3,08t-0,5t2-0,01t3+S2(t); Y2(t)=374;
для третьего года трехлетнего цикла
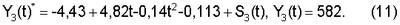
Значения S1(t), S2(t), S3(t) можно получить подстановкой значений из таблицы 3 в уравнение (10). Величина ошибки, соответствующая выбранной модели, представлена в таблице 3.
В таблице 4 представлены результаты проверки прогноза заболеваемости КЭ.
Таблица 4
Результаты проверки прогноза заболеваемости КЭ |
| Годы цикла |
Прогнозируемое количество случаев КЭ |
Календарный год |
Фактическая заболеваемость |
Процент снижения заболеваемости в результате проведения профилактических мероприятий за |
| |
|
|
текущий год |
год трехлетнего цикла |
текущий год |
год трехлетнего цикла |
| 1 год |
318 |
1994 |
140 |
177 |
56,0 |
44,3 |
| 1997 |
265 |
16,7 |
| 2000 |
126 |
60,4 |
| 2 год |
374 |
1995 |
217 |
267 |
42,0 |
28,6 |
| 1998 |
318 |
15,0 |
| 2001 |
266 |
28,9 |
| 3 год |
582 |
1996 |
478 |
370 |
17,9 |
36,4 |
| 1999 |
476 |
18,2 |
| 2002 |
158 |
72,8 |
Предложенный способ позволяет прогнозировать показатели заболеваемости КЭ в течение эпидемического сезона года и в отдельный период с пятидневным интервалом, а также проверять эффективность проведения противоэпидемических мероприятий в течение эпидемического сезона и планировать наиболее эффективные меры борьбы против данной инфекции.
Примеры конкретного выполнения предлагаемого способа
Пример 1
По данным ФГУЗ “Центр гигиены и эпидемиологии в Тюменской области” на юге Тюменской области с 1994 по 2002 гг. регистрируется заболеваемость КЭ с периодическим ростом и снижением в отдельные годы. Установлена цикличность заболеваемости с интервалом в 3 года.
Проведен расчет предполагаемой заболеваемости КЭ за 2003 год, который соответствует 1-му году трехлетнего цикла.
Учет заболеваний КЭ провели за промежутки времени, равные 5 дням, в течение временного ряда t от 1 до 36 значений за 1994, 1997 и 2000 годы. Временной ряд представлен в табл.5.
Таблица 5
Дни учета заболеваний в период временного интервала t |
| Временной ряд t |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
| Месяцы учета заболеваний |
апрель |
май |
| Дни учета заболеваний |
1-5 |
6-10 |
11-15 |
16-20 |
21-25 |
26-30 |
1-5 |
6-10 |
11-15 |
16-20 |
21-25 |
26-30 |
| Количество дней (х) |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
50 |
55 |
60 |
| Временной ряд t |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
| Месяцы учета заболеваний |
июнь |
июль |
| Дни учета заболеваний |
до-5 |
6-10 |
11-15 |
16-20 |
21-25 |
26-30 |
1-5 |
6-10 |
11-15 |
16-20 |
21-25 |
26-30 |
| Количество дней (х) |
65 |
70 |
75 |
80 |
85 |
90 |
95 |
100 |
105 |
110 |
115 |
120 |
| Временной ряд t |
25 |
26 |
27 |
28 |
29 |
30 |
31 |
32 |
33 |
34 |
35 |
36 |
| Месяцы учета заболеваний |
август |
сентябрь |
| Дни учета заболеваний |
до-5 |
6-10 |
11-15 |
16-20 |
21-25 |
26-30 |
1-5 |
6-10 |
11-15 |
16-20 |
21-25 |
26-30 |
| Количество дней (х) |
125 |
130 |
135 |
140 |
145 |
150 |
155 |
160 |
165 |
170 |
175 |
180 |
Расчет временного интервала t проводим по формуле 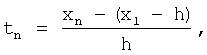
где xn=180; x0=0 (начало отсчета);
x1=5 и соответствует временному интервалу 1 (t1=1);
h – шаг интервала, равный 5 дням (h=5);
t дает значения от 1 до 36 (tn=1, 2, 3, …, 36).
Определили показатель сглаживания сезонной составляющей S(t), который для первого года трехлетнего цикла соответствует S1(t). При этом 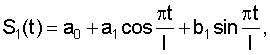
где а0=0; a1=-0,111, b1=2,155, 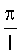 соответствует 6 соответствует 6 . Прогноз заболеваемости КЭ проводили по формуле: Y1(t)*=-4,48+5,15t-0,41t2+0,01t3+S1(t); Y1(t)=318. . Прогноз заболеваемости КЭ проводили по формуле: Y1(t)*=-4,48+5,15t-0,41t2+0,01t3+S1(t); Y1(t)=318.
Фактическая заболеваемость за 2003 год составила 98 случаев. Снижение заболеваемости за счет проводимых профилактических мероприятий составило 69,2%.
Пример 2
По данным ФГУЗ “Центр гигиены и эпидемиологии в Тюменской области” на юге Тюменской области с 1994 по 2003 гг. регистрируется заболеваемость КЭ с периодическим ростом и снижением в отдельные годы. Установлена цикличность заболеваемости с интервалом в 3 года.
Проведен расчет предполагаемой заболеваемости КЭ за 2004 год, который соответствует 2-му году трехлетнего цикла. Учет заболеваний КЭ провели за промежутки времени, равные 5 дням, в течение временного ряда t от 1 до 36 значений за 1995, 1998 и 2001 годы.
Определили показатель сглаживания сезонной составляющей – S(t), который для второго года трехлетнего цикла соответствует S2(t). При этом 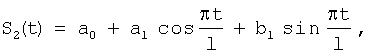
где a0=0; а1=-0,977, b1=4,619, 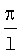 соответствует 6 соответствует 6 . Прогноз заболеваемости КЭ проводили по формуле: . Прогноз заболеваемости КЭ проводили по формуле:
Y2(t)*=-2,44+3,08t-0,5t2-0,01t3+S2(t),
Y2(t)=374.
Фактическая заболеваемость за 2004 год составила 133 случая. Снижение заболеваемости за счет проводимых профилактических мероприятий составило 64,4%.
Анализируя эффективность проведения профилактических мероприятий за последние 2 года можно отметить, что она составила 66,8%. Поэтому при условии проведения профилактических мероприятий с том же объеме заболеваемость КЭ в 2005 г. составит 33,2% от прогнозируемой заболеваемости в течение третьего года трехлетнего цикла, т.е. 193 случая. Фактически в 2005 г. зарегистрировано 218 случаев КЭ.
Пример 3
По данным ФГУЗ “Центр гигиены и эпидемиологии в Тюменской области” на юге Тюменской области с 1994 по 2004 гг. регистрируется заболеваемость иксодовым клещевым боррелиозом (ИКБ) с периодическим ростом и снижением в отдельные годы.
За период с 1994 по 2002 гг. сформированы ряды чисел заболеваемости ИКБ с пятидневным интервалом с 1 апреля по 30 сентября по материалам карт эпидемиологического обследования больных, составлены ежегодные временные ряды, состоящие из 36 значений.
Определили среднее количество заболеваний за 5 дней в течение апреля-июня и июля-сентября трехгодичного цикла за 9-12 лет и средние параметры заболеваемости ИКБ (фиг.6). Выявлена трехлетняя цикличность заболеваний ИКБ по показателям заболеваемости за пятидневный интервал. Установлена также трехлетняя цикличность заболеваний ИКБ по параметрам биологических ритмов экосистемы (возбудитель инфекции – боррелии, переносчик – иксодовые клещи и многочисленные прокормители клещей) (табл.6).
По методике, описанной в примере 1, и согласно формуле изобретения определили показатели заболеваемости ИКБ за первый, второй и третий годы трехлетнего цикла, которые составили соответственно: Y1(t)=190; Y2(t)=199; Y3(t)=351.
Таблица 6
Параметры ритмов заболеваемости ИКБ |
| Длительность ритма |
Сутки [годы] |
Амплитуда ± se (количество заболеваний) |
Акрофаза ± se (градусы) |
Мезор ± se (количество заболеваний) |
| Окологодовой |
365 [1] |
4,6±0,3 |
-119±5 |
4,6±0,3 |
| Околотрехлетний |
1095 [3] |
1,8±0,4 |
-141±14 |
|
| Параметры наилучшей апроксимации для околотрехлетнего цикла |
992±25 [2,72±0,06] |
1,9±0,3 |
-230±10 |
|
Фактическая заболеваемость ИКБ в 2003 г. (1-й год трехлетнего цикла) составила 143; в 2004 г. (второй год трехлетнего цикла) – 149. Процент снижения заболеваемости в 2003 г. составил 24,7%, а в 2004 г. – 25,1%. Учитывая, что при ИКБ серопрофилактика и вакцинопрофилактика не проводятся, надо полагать, что снижение заболеваемости связано с проведением акарицидных обработок в природных очагах инфекции. Если в 2005 г. акарицидные обработки будут проведены на тех же территориях и в том же объеме, то на территории юга Тюменской области в 2005 г. будет зарегистрировано 264 случая ИКБ, т.е. 75,1% от расчетного показателя заболеваемости в третьем году трехлетнего цикла.
Сущность предложенного способа заключается в том, что временной ряд заболеваемости КИ отражает экологические факторы, влияющие на возбудителей инфекций, переносчиков, их прокормителей и экологию населения, проживающего на территориях с высоким риском заболеваемости КИ.
Предлагаемый способ прост, легко осуществим, не требует больших материальных затрат.
Формула изобретения
Способ прогноза заболеваемости клещевыми инфекциями (КИ), отличающийся тем, что прогноз заболеваемости КИ осуществляют по учету заболеваемости КИ за промежутки времени, равные 5 дням, в течение временного ряда – t, определяют показатель сглаживания сезонной составляющей – S(t), которая для первого года трехлетнего цикла соответствует S1(t), для второго года – S2(t), для третьего года – S3(t), при этом 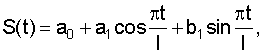
где а0=0; a1: для S1(t) соответствует “-0,111”, для S2(t) соответствует “-0,977”, а для S3(t) соответствует “0,362”; b1: для S1(t) соответствует “2,155”, для S2(t) соответствует “4,619”, а для S3(t) соответствует “-1,813”;  /l: для S1(t) соответствует 6 /l: для S1(t) соответствует 6 , для S2(t) соответствует 6 , для S2(t) соответствует 6 , а для S3(t) соответствует 7,6 , а для S3(t) соответствует 7,6 ; l – число периодов тригонометрических функций, которые выбирают в соответствии с числом максимумов временного ряда; прогноз заболеваемости КИ проводят по следующим формулам, позволяющим определить прогнозируемое количество случаев заболеваний КИ за временной интервал: для первого года трехлетнего цикла Y1(t)*=-4,48+5,15t-0,41t2+0,01t3+S1(t); для второго года трехлетнего цикла Y2(t)*=-2,44+3,08t-0,5t2-0,01t3+S2(t); для третьего года трехлетнего цикла Y3(t)*=-4,43+4,82t-0,14t2-0,1t3+S3(t). ; l – число периодов тригонометрических функций, которые выбирают в соответствии с числом максимумов временного ряда; прогноз заболеваемости КИ проводят по следующим формулам, позволяющим определить прогнозируемое количество случаев заболеваний КИ за временной интервал: для первого года трехлетнего цикла Y1(t)*=-4,48+5,15t-0,41t2+0,01t3+S1(t); для второго года трехлетнего цикла Y2(t)*=-2,44+3,08t-0,5t2-0,01t3+S2(t); для третьего года трехлетнего цикла Y3(t)*=-4,43+4,82t-0,14t2-0,1t3+S3(t).
РИСУНКИ
MM4A – Досрочное прекращение действия патента СССР или патента Российской Федерации на изобретение из-за неуплаты в установленный срок пошлины за поддержание патента в силе
Дата прекращения действия патента: 27.04.2008
Извещение опубликовано: 10.06.2010 БИ: 16/2010
|
|