|
|
(21), (22) Заявка: 2004138069/28, 24.12.2004
(24) Дата начала отсчета срока действия патента:
24.12.2004
(43) Дата публикации заявки: 10.06.2006
(46) Опубликовано: 10.02.2007
(56) Список документов, цитированных в отчете о
поиске:
ХРЕНОВ Л.С. Геодезия. – М.: Гослесбумиздат, 1955, с.428-436. SU 1565359 A1, 23.05.1990. КУЗНИК И.А., ЛУКОНИН Е.И., ПИЛИПЕНКО В.Я. Гидрология и гидрометрия. – М.: Колос, 1968, с.72, 73. CN 1116704 А, 14.02.1996.
Адрес для переписки:
424024, г.Йошкар-Ола, пл. Ленина, 3, МарГТУ, отдел интеллектуальной собственности
|
(72) Автор(ы):
Мазуркин Петр Матвеевич (RU),
Иванов Алексей Андреевич (RU)
(73) Патентообладатель(и):
Марийский государственный технический университет (RU)
|
(54) СПОСОБ ИЗМЕРЕНИЯ ПЛОЩАДИ ВОДОСБОРА РАВНИННОЙ РЕКИ ПО ДЛИНАМ ПРИТОКОВ
(57) Реферат:
Изобретение относится к гидрологии рек и может быть использовано при оценке водных ресурсов. Сущность: измеряют длину притоков реки. Измеряют площадь водосбора притоков. Все притоки располагают отдельно по убыванию длины и отдельно по убыванию площади водосбора. Присваивают ранги каждому притоку, начиная с единицы. Затем в ранговых распределениях выделяют группы притоков по измеренным и неизмеренным значениям длины притоков или площади водосборов этих же притоков. По измеренным притокам реки по их длине и площади водосбора выявляют закономерности распределения отдельно по убыванию длины притоков и отдельно по убыванию площади водосбора притоков. По найденным закономерностям распределения вычисляют ориентировочные значения площади водосбора неизмеренных притоков. Технический результат: повышение точности измерений. 7 з.п. ф-лы, 4 табл.
Изобретение относится к гидрологии рек и водосборным бассейнам речных сетей и может быть использовано при оценке водных ресурсов.
Известен способ измерения площади водосбора равнинной реки по длинам притоков (см. учебник: Важнов А.Н. Гидрология рек. Учебник для студентов спец. «География». – М.: МГУ, 1976. – 339 с.- С.47-48), включающий измерение длины притоков реки (натурные измерения или измерения длин по картам), классификацию измеренных притоков реки по Р.Хортону по различным порядкам водотоков, начиная от самых малых неразветвленных притоков, вычисление суммы длин водотоков данного порядка, вычисление средней длины притоков каждого порядка делением суммы длин на количество водотоков данного порядка, вычисление отношения средней длины притоков данного порядка к средней длине притоков следующего более низкого порядка, учет коэффициента бифуркации числа притоков (данного порядка водотоков по принадлежности к реке, то есть к основному водотоку) в зависимости от типа местности.
Недостатком этого способа является то, что расчеты по средним арифметическим длинам притоков не дают достаточной для практической гидрологии точности вычислений площади водосбора, прежде всего при наличии неизмеренных территорий водосборов притоков. При этом практически невозможно определить площади водосбора у неизмеренных (по значениям площади водосбора) притоков.
Известен также способ измерения площади водосбора равнинной реки по длинам притоков (см. учебник: Важнов А.Н. Гидрология рек. Учебник для студентов спец. «География». – М.: МГУ, 1976. – 339 с. – С.58-59), включающий измерение длины притоков реки (натурные измерения, измерения длин по картам или по сведениям, полученным от местных жителей), измерение площади водосбора в натуре (геодезическими приемами аэрофотосъемки или космической съемки) или по карте с помощью планиметра или палетки (инструментальные способы картометрии), или непосредственно на местности, используя наземные геодезические приемы и приборы, использование среднестатистической формулы 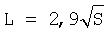 , где L – длина реки (притока), км, S – площадь водосбора притока или всей реки, км2, для больших рек бывшей СССР, Китая и США в виде эмпирической модели для описания связи между площадью бассейна и длиной реки по измеренным притокам реки, а по неизмеренным притокам вычисление расчетного значения площади притока выполняется по указанной эмпирической формуле. , где L – длина реки (притока), км, S – площадь водосбора притока или всей реки, км2, для больших рек бывшей СССР, Китая и США в виде эмпирической модели для описания связи между площадью бассейна и длиной реки по измеренным притокам реки, а по неизмеренным притокам вычисление расчетного значения площади притока выполняется по указанной эмпирической формуле.
Недостатком прототипа является то, что применение простой среднестатистической для бывшей ССР, Китая и США эмпирической зависимости не дает высокой точности. При этом прототип не предусматривает определение площади водосбора при ориентировочном значении длины притока, а также не может быть решена обратная задача по определению длины притока, если известна площадь его водосбора. Эмпирическую формулу можно записать еще в виде L=2,950,5, то есть в форме закона аллометрического роста. Причем оба параметра этой модели, активность роста 2,9 (для небольших бассейнов речной сети рекомендуется коэффициент около 1,6) и интенсивность роста 0,5 являются грубо приближенными. Эта формула недостаточно объективно описывает конкретную речную сеть.
Технический результат – повышение точности учета водных ресурсов и снижение погрешности описания закономерности взаимосвязи между показателями реки и ее притоков по площади и длине.
Этот технический результат достигается тем, что все притоки реки располагают отдельно по убыванию длины и отдельно по убыванию площади, присваивают ранги каждому притоку, начиная с единицы, после этого в этих ранговых распределениях выделяют группы притоков по измеренным и неизмеренным значениям длины притоков или площади водосборов, по измеренным притокам реки по их длине и площади водосбора выявляют закономерности распределения отдельно по убыванию длины и отдельно по убыванию площади, а затем по найденным закономерностям распределения с использованием эмпирической формулы S=f(L) вычисляют ориентировочные значения площади водосбора неизмеренных притоков.
Ранги присваивают от единицы и более целыми числами в порядке убывания длины притока и площади его водосбора по всем притокам, содержащие как измеренные, так и измеренные по карте или в натуре параметры длины и площади.
Группу неизмеренных притоков разделяют на подгруппы: во-первых, притоки с измеренными длинами, но с неизвестными значениями площади водосбора; во-вторых, притоки с ориентировочно по данным местных жителей значениями длины и с неизвестными значениями площади водосбора; в-третьих, притоки, у которых известны только ранговое расположение среди измеренных притоков; в-четвертых, притоки, у которых известны значения площади водосбора, но не известны значения длины (обратная задача). Причем все измеренные и неизмеренные притоки дополнительно измеряют по картам, фотографиям аэрофотосъемки или другими известными способами для уточнения исходных данных.
Из всех измеренных и неизмеренных притоков в процессе ранжирования исключаются притоки, у которых по различным причинам отсутствует водоток, а также притоки более высоких порядков Р.Хортона, то есть оставляются для статистического моделирования действующие притоки первого и второго порядков при условии, что значения длины и площади притоков второго порядка незначимо отличаются от максимальных значений длины и площади наибольшего притока первого порядка.
По измеренным и уточненным притокам реки по их длине и площади водосбора выявляют закономерности распределения отдельно по убыванию длины и отдельно по убыванию площади водосбора по формуле:
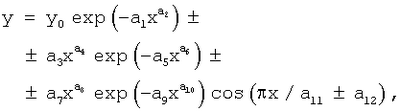
где y – показатели притока реки (длина притока L, км, или площадь водосбора S, км2), y0 – теоретически возможное максимальное значение показателя для данной речной сети, х – ранг значений длины притока rL или ранг значений площади водосбора rS, а1…а12 – параметры статистической модели, при значениях, равных нулю или единице, в некоторых из них происходит изменение структуры уравнения (например, чаще всего а6=1, а10=1, a8=0 или a9=0).
Вместо среднестатистической формулы используют эмпирическую формулу S=f(L), полученную по значениям длины и площади водосбора измеренных притоков, которую определяют по формуле:
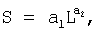
где S – площадь водосбора притока, км2, L – длина водотока, км, а1, а2 – параметры статистической модели (причем в частных случаях может быть a2=0,5).
По найденным закономерностям распределения длины и площади водосбора измеренных и уточненных после экспериментальных измерений, а также по полученной эмпирической формуле сопоставленных расчетных значений принимают значения площади водосбора неизмеренных притоков.
Для окончательного выяснения достоверных значений площади водосбора у неизмеренных притоков, а также уточнения значений длины и площади водосбора у измеренных ранее притоков дополнительно проводят полевые исследования, причем по отклонениям от ранее проведенных полевых исследований судят о динамике длины и площади водосборов отдельных притоков.
Сущность технического решения заключается в том, что давно известна эвристическая закономерность: чем длиннее река, тем больше в равнинных условиях ее площадь водосбора (см. например: Важнов А.Н. – С.59). Поэтому показатели длины и площади притоков отдельной речной системы должны располагаться (распределяться) одинаково по убыванию значений каждого из показателей. Таким образом, ранжируя притоки в порядке возрастания (что оказалось недостаточно корректным для выявления законов распределения) или убывания их длины, происходит ранжирование этих притоков и по площади водосбора. Однако не все речные системы имеют полное описание по длине и площади своих притоков. Многие речные системы все еще недостаточно исследованы и измерены, поэтому существуют четыре группы притоков: 1) притоки, у которых имеются измеренные длины и площади; 2) притоки, у которых имеют измеренные длины, но отсутствуют значения площади водосбора; 3) притоки речной системы, у которых имеются значения площади, но отсутствуют длины (этот вариант редкий, но теоретически такая обратная задача вполне возможна); 4) притоки, у которых нет точных измеренных значений как по длине притока, так и по площади водосбора (необходимо найти ориентировочное значение длины притока по сведениям, полученным от местных жителей, а также известными частными расстояниями между сооружениями или населенными пунктами на данном притоке реки); 5) притоки, у которых неизвестные измеренные значения длины и площади, но известно хотя бы его место среди других по рангу; 6) притоки по п.п.1-5, у которых на момент исследования нет водотока (высохший приток).
Положительный эффект достигается тем, что могут быть вычислены с достаточной для практических гидрологических расчетов площади водосбора и по тем притокам, у которых не были измерены значения площади, но известны точно (по измерениям на карте или в натуре) или приближенно (например, по сведениям местных жителей) значения длины притока. Приближенно могут быть определены параметры притоков и по неизмеренным их длинам и площади, если известно ранговое расположение среди измеренных притоков.
Новизна технического решения заключается в том, что впервые эвристическая связь между значениями длины и площади измеренных притоков речной системы преобразуется в закономерности распределения каждого из этих показателей, а затем по найденным статистическим закономерностям обоих распределений определяются (рассчитываются) неизмеренные площади притоков. При этом возможна и обратная задача, когда по ориентировочно известной площади водосбора притока определяется его длина.
Предлагаемое техническое решение обладает существенными признаками, новизной и значительным положительным эффектом. Материалов, порочащих новизну технического решения, нами не обнаружено
Способ измерения площади водосбора равнинной реки по длинам притоков включает в себя следующие действия.
Вначале все притоки реки располагают отдельно по убыванию длины и отдельно по убыванию площади. После этого присваивают ранги каждому притоку, начиная с единицы. Затем в полученных ранговых распределениях выделяют две группы притоков по измеренным и неизмеренным значениям длины притоков или площади водосборов. По первой группе, то есть по измеренным (до проведения моделирования) притокам реки по их длине и площади водосбора выявляют закономерности распределения отдельно по убыванию длины и отдельно по убыванию площади. Затем по найденным закономерностям распределения с использованием эмпирической формулы S=f(L) вычисляют ориентировочные значения площади водосбора неизмеренных притоков.
Ранги присваивают от единицы и более целыми числами в порядке убывания длины притока и площади его водосбора по всем притокам, содержащим как измеренные, так и измеренные по карте или в натуре параметры длины и площади.
Группу неизмеренных притоков разделяют на несколько подгрупп (в конкретной группе неизмеренных притоков могут оказаться не все указанные подгруппы): во-первых, притоки с измеренными длинами, но с неизвестными значениями площади водосбора; во-вторых, притоки с ориентировочно по данным местных жителей значениями длины и с неизвестными значениями площади водосбора; в-третьих, притоки, у которых известны только ранговое расположение среди измеренных притоков; в-четвертых, притоки, у которых известны значения площади водосбора, но не известны значения длины (обратная задача). Причем все измеренные и неизмеренные притоки дополнительно измеряют по картам, фотографиям аэрофотосъемки или другими известными способами для уточнения исходных данных.
Из всех измеренных и неизмеренных притоков в процессе ранжирования исключаются притоки, у которых по различным причинам отсутствует водоток, а также притоки более высоких порядков Р.Хортона, то есть оставляются для статистического моделирования действующие притоки первого и второго порядков при условии, что значения длины и площади притоков второго порядка незначимо отличаются от максимальных значений длины и площади наибольшего притока первого порядка.
По измеренным и уточненным притокам реки по их длине и площади водосбора выявляют закономерности распределения отдельно по убыванию длины и отдельно по убыванию площади водосбора по формуле:
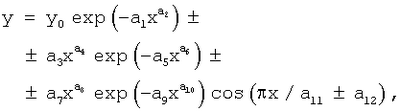
где y – показатели притока реки (длина притока L, км, или площадь водосбора S, км2), y0 – теоретически возможное максимальное значение показателя для данной речной сети, х – ранг значений длины притока rL или ранг значений площади водосбора rS, а1…а12 – параметры статистической модели при значениях, равных нулю или единице, некоторых из них происходит изменение структуры уравнения (например, чаще всего а6=1, а10=1, а8=0 или а9=0).
Вместо среднестатистической формулы используют эмпирическую формулу S=f(L), полученную по значениям длины и площади водосбора измеренных притоков, которую определяют по формуле:
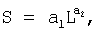
где S – площадь водосбора притока, км2, L – длина водотока, км, а1, а2 – параметры статистической модели (причем в частных случаях может быть а2=0,5).
По найденным закономерностям распределения длины и площади водосбора у притоков, измеренных и уточненных после экспериментальных измерений, а также по полученной эмпирической формуле сопоставленных по расчетным значениям принимают значения площади водосбора неизмеренных притоков.
Для окончательного выяснения достоверных значений площади водосбора у неизмеренных притоков, а также уточнения значений длины и площади водосбора у измеренных ранее притоков дополнительно проводят полевые исследования, причем по отклонениям от ранее проведенных полевых исследований судят о динамике длины и площади водосборов отдельных притоков.
Способ измерения площади водосбора равнинной реки по длинам притоков выполняется, например, при измерении параметров притоков малой реки следующим образом.
Как правило, почти все реки в нашей стране имеют неполное информационное описание и, что весьма удивительно, имея явные преимущества в космических и иных исследованиях, очень мало результатов точных картографических и картометрических исследований. Ныне пользуемся картами, составленными весьма небрежно 20-30 и более лет назад. И это серьезно сдерживает работы по земельному кадастру, по природообустройству, по учету водных и других природных ресурсов.
По информации и прошлых измерениях речной сети, полученной 20-30 и более лет назад, все притоки реки располагают отдельно по убыванию длины и отдельно по убыванию площади, присваивают ранги каждому притоку, начиная с единицы. После этого в этих ранговых распределениях выделяют группы притоков по измеренным и неизмеренным значениям длины притоков или площади водосборов, по измеренным притокам реки по их длине и площади водосбора выявляют закономерности распределения отдельно по убыванию длины и отдельно по убыванию площади, а затем по найденным закономерностям распределения с использованием эмпирической формулы S=f(L) вычисляют ориентировочные значения площади водосбора неизмеренных притоков.
Ранги присваивают от единицы и более целыми числами в порядке убывания длины притока и площади его водосбора по всем притокам, содержащим как измеренные, так и измеренные по карте или в натуре параметры длины и площади.
Группу неизмеренных притоков разделяют в общем случае на следующие подгруппы: во-первых, притоки с измеренными длинами, но с неизвестными значениями площади водосбора; во-вторых, притоки с ориентировочно по данным местных жителей значениями длины и с неизвестными значениями площади водосбора; в-третьих, притоки, у которых известны только ранговое расположение среди измеренных притоков; в-четвертых, притоки, у которых известны значения площади водосбора, но не известны значения длины (обратная задача). Причем все измеренные и неизмеренные притоки дополнительно измеряют по картам, фотографиям аэрофотосъемки или другими известными способами для уточнения исходных данных.
Из всех измеренных и неизмеренных притоков в процессе ранжирования исключаются притоки, у которых по различным причинам отсутствует водоток, а также притоки более высоких порядков Р.Хортона, то есть оставляются для статистического моделирования действующие притоки первого и второго порядков при условии, что значения длины и площади притоков второго порядка незначимо отличаются от максимальных значений длины и площади наибольшего притока первого порядка.
По измеренным и уточненным притокам реки по их длине и площади водосбора выявляют закономерности распределения отдельно по убыванию длины и отдельно по убыванию площади водосбора по формуле:
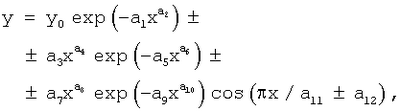
где y – показатели притока реки (длина притока L, км, или площадь водосбора S, км2), y0 – теоретически возможное максимальное значение показателя для данной речной сети, х – ранг значений длины притока rL или ранг значений площади водосбора rS, а1…а12 – параметры статистической модели, при значениях, равных нулю или единице, некоторых из них происходит изменение структуры уравнения (например, чаще всего а6=1, а10=1, а8=0 или а9=0).
Вместо среднестатистической формулы используют эмпирическую формулу S=f(L), полученную по значениям длины и площади водосбора измеренных притоков, которую определяют по формуле:
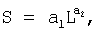
где S – площадь водосбора притока, км2, L – длина водотока, км, a1, а2 – параметры статистической модели (причем в частных случаях может быть a2=0,5).
По найденным закономерностям распределения длины и площади водосбора измеренных и уточненных после экспериментальных измерений, а также по полученной эмпирической формуле сопоставленных расчетных значений принимают значения площади водосбора неизмеренных притоков.
Для окончательного выяснения достоверных значений площади водосбора у неизмеренных притоков, а также уточнения значений длины и площади водосбора у измеренных ранее притоков дополнительно проводят полевые исследования, причем по отклонениям от ранее проведенных полевых исследований судят о динамике длины и площади водосборов отдельных притоков.
Пример. Данные по реке Шклея, расположенной на территории республики Марий Эл, приведены в нижеследующей табл.1. Здесь показаны два состояния водотоков – до и после проведения полевых исследований по уточнению значений длины и площади притоков. Предметом данного технического решения является информационное состояние реки, полученное до проведения уточненных исследований. Поэтому 25 притоков имеют значения длины, часть из притоков не имеет по литературным сведениям значений площади водосбора. Поэтому требуется проводить анализ по реке с недостающими сведениями по некоторым притокам.
Таблица 1
Речная сеть бассейна Шклея (21 пр. пр. р. Рутка) |
| № п/п |
Название притока реки |
Порядок водотока |
Сведения о притоках по литературе до проведения исследования |
Сведения о притоках после проведения исследования |
| Длина L, км |
Площадь водосбора S, км2 |
Длина L, км |
Площадь водосбора S, км2 |
| 1 |
1 пр. пр. |
1 |
0,6 |
– |
0,6 |
3,25 |
| 2 |
2 л. пр. |
1 |
2,1 |
– |
2,1 |
5,75 |
| 3 |
3 л. пр. |
1 |
2,9 |
6,5 |
2,9 |
6,50 |
| 4 |
4 л. пр. |
1 |
1,7 |
– |
1,7 |
1,60 |
| 5 |
5 л. пр. |
1 |
1,1 |
– |
1,1 |
1,00 |
| 6 |
6 пр. пр. |
2 |
3,6 |
10,1 |
3,6 |
10,10 |
| 7 |
1 л. пр. 6-го пр. |
1 |
0,3 |
– |
0,3 |
0,55 |
| 8 |
2 л. пр. 6-го пр. |
1 |
0,6 |
– |
0,6 |
0,50 |
| 9 |
3 пр. пр. 6-го пр. |
1 |
0,8 |
– |
0,8 |
2,60 |
| 10 |
7 пр. пр. |
1 |
1,7 |
– |
1,7 |
2,10 |
| 11 |
8 пр. пр. |
2 |
3,8 |
11,9 |
3,8 |
11,90 |
| 12 |
1 л. пр. 8-го пр. |
1 |
1,4 |
– |
1,4 |
0,90 |
| 13 |
2 л. пр. 8-го пр. |
1 |
2,1 |
– |
Нет водотока |
Нет водотока |
| 14 |
9 пр. пр. |
2 |
4,0 |
11,9 |
4,0 |
11,90 |
| 15 |
1 л. пр 9-го пр. |
1 |
1,5 |
– |
1,5 |
3,00 |
| 16 |
10 л. пр. |
2 |
5,1 |
15,2 |
4,8 |
15,20 |
| 17 |
1 л. пр. 10-го пр. |
1 |
1,6 |
– |
1,6 |
3,80 |
| 18 |
11 пр. пр. |
1 |
2,2 |
8,3 |
2,2 |
8,30 |
| 19 |
12 пр. пр. |
2 |
9,1 |
16,6 |
5,5 |
16,60 |
| 20 |
1 пр. пр. 12-го пр. |
1 |
1,7 |
– |
1,3 |
3,60 |
| 21 |
2 л. пр.12-гопр. |
1 |
0,9 |
– |
3,5 |
6,75 |
| 22 |
13 пр. пр. |
1 |
6,9 |
8,6 |
3,4 |
8,60 |
| 23 |
14 пр. пр |
1 |
3,5 |
– |
1,6 |
3,25 |
| 24 |
15 пр. пр. |
2 |
5,3 |
10,1 |
1,8 |
10,10 |
| 25 |
1 л. пр. 15-гопр. |
1 |
3,0 |
Нет водотока |
Нет водотока |
Нет водотока |
| 26 |
2 л. пр. (ниже 1пр. пр.+) |
1 |
– |
– |
1,0 |
1,90 |
| 27 |
1 пр. пр. + (ниже 2л. пр.) |
1 |
– |
– |
2,0 |
6,20 |
Сравнение водотоков по порядкам показывает, что притоки второго порядка по максимум длины отличаются только в 9,1/6,9=1,32 раза. Поэтому в статистическом анализе участвуют все притоки. Из них один приток №25 оказался без воды (водой наполняется приток только весной в половодье). Как видно из данных табл.1, мелкие притоки первого порядка в основном не были исследованы и поэтому не получили значений площади водосбора.
Для моделирования вначале расставим ранги по убыванию длины притока. При этом точность значений длины составляет 0,1 км, поэтому тем значениям длины притоков, которые отличаются только на 0,1 км, присваиваются одинаковые ранги.
После моделирования устойчивыми законами получена статистическая модель в виде формулы
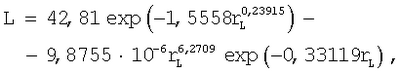
где L – длина водотока, км, rL – ранг длины притока реки.
Результаты вычислений по модели приведены в табл.2.
Таблица 2
Ранговое распределение притоков реки Шклея (21 пр. пр. р. Рутка) по длине, км |
| № п/п |
Название притока реки |
Порядок водотока |
Ранг rL |
Факт 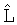 |
Расчетные значения |
| L |
 |
 , % , % |
| 1 |
1 пр. пр. |
1 |
15 |
0,6 |
0.56 |
0.04 |
6.67 |
| 2 |
2 л. пр. |
1 |
10 |
2,1 |
2.21 |
-0.11 |
-5.24 |
| 3 |
3 л. пр. |
1 |
9 |
2,9 |
2.60 |
0.30 |
10.34 |
| 4 |
4 л. пр. |
1 |
11 |
1,7 |
1.83 |
-0.13 |
-7.65 |
| 5 |
5 л. пр. |
1 |
13 |
1,1 |
1.13 |
-0.03 |
-2.73 |
| 6 |
6 пр. пр. |
2 |
7 |
3,6 |
3.40 |
0.20 |
5.56 |
| 7 |
1 л. пр. 6-го пр. |
1 |
16 |
0,3 |
0.34 |
-0.04 |
-13.33 |
| 8 |
2 л. пр. 6-го пр. |
1 |
15 |
0,6 |
0.56 |
0.04 |
6.67 |
| 9 |
3 пр. пр. 6-го пр. |
1 |
14 |
0,8 |
0.83 |
-0.03 |
-3.75 |
| 10 |
7 пр. пр. |
1 |
11 |
1,7 |
1.83 |
-0.13 |
-7.65 |
| 11 |
8 пр. пр. |
2 |
6 |
3,8 |
3.83 |
-0.03 |
-0.79 |
| 12 |
1 л. пр. 8-го пр. |
1 |
12 |
1,4 |
1.47 |
-0.07 |
-5.00 |
| 13 |
2 л. пр. 8-го пр. |
1 |
8 |
2,1 |
2.90 |
0.11 |
3.55 |
| 14 |
9 пр. пр. |
2 |
5 |
4,0 |
4.31 |
-0.31 |
-7.75 |
| 15 |
1 л. пр. 9-го пр. |
1 |
12 |
1,5 |
1.47 |
0.03 |
2.00 |
| 16 |
10 л. пр. |
2 |
4 |
5,1 |
4.89 |
0.21 |
4.12 |
| 17 |
1 л. пр. 10-го пр. |
1 |
12 |
1,6 |
1.47 |
0.13 |
8.13 |
| 18 |
11 пр. пр. |
1 |
10 |
2,2 |
2.21 |
-0.01 |
-0.45 |
| 19 |
12 пр. пр. |
2 |
1 |
9,1 |
9.03 |
0.07 |
0.77 |
| 20 |
1 пр. пр. 12-го пр. |
1 |
11 |
1,7 |
1.83 |
-0.13 |
-7.65 |
| 21 |
2 л. пр. 12-го пр. |
1 |
14 |
0,9 |
0.83 |
0.07 |
7.78 |
| 22 |
13 пр. пр. |
1 |
2 |
6,9 |
6.82 |
0.08 |
1.16 |
| 23 |
14 пр. пр |
1 |
7 |
3,5 |
3.40 |
0.10 |
2.86 |
| 24 |
15 пр. пр. |
2 |
3 |
5,3 |
5.66 |
-0.36 |
-6.79 |
Здесь: 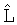 – фактические значения показателя; L – расчетные значения показателя; – фактические значения показателя; L – расчетные значения показателя;  – остаток, то есть разница – остаток, то есть разница 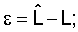  – относительная погрешность по формуле – относительная погрешность по формуле 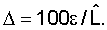 При этом достоверность формулы оценивается по значению При этом достоверность формулы оценивается по значению  max, которое в таблице подчеркнуто. Доверительная вероятность будет равна 100- max, которое в таблице подчеркнуто. Доверительная вероятность будет равна 100- max. max. |
Введение третьей (волновой) составляющей не приносит существенного повышения точности статистической модели, поэтому предыдущую формулу, состоящую из двух составляющих, оставляем без дополнения третьей составляющей.
Далее рассмотрим распределение значений площади водосбора притоков, показанных в табл.1. После моделирования была получена формула
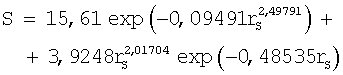
с максимальной относительной погрешностью 4,58%. С дополнением третьей волновой составляющей была получена закономерность (табл.3)
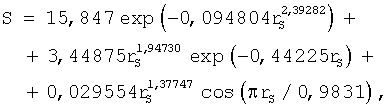
где rS – ранг значений площади водосбора.
Таблица 3
Ранговое распределение притоков реки Шклея по площади водосбора, км2 |
| № п/п |
Название притока реки |
Порядок водотока |
Ранг rS |
Факт 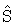 |
Расчетные значения |
| S |
 |
 , % , % |
| 3 |
3 л. пр. |
1 |
7 |
6.5 |
6.50 |
0.00 |
0.00 |
| 6 |
6 пр. пр. |
2 |
4 |
10.1 |
10.10 |
0.00 |
0.00 |
| 11 |
8 пр. пр. |
2 |
3 |
11.9 |
11.90 |
-0.00 |
-0.00 |
| 14 |
9 пр. пр. |
2 |
3 |
11.9 |
11.90 |
-0.00 |
-0.00 |
| 16 |
10 л. пр. |
2 |
2 |
15.2 |
15.20 |
0.00 |
0.00 |
| 18 |
11 пр. пр. |
1 |
6 |
8.3 |
8.30 |
-0.00 |
-0.00 |
| 21 |
2 л. пр. 12-го пр. |
1 |
1 |
16.6 |
16.60 |
-0.00 |
-0.00 |
| 22 |
13 пр. пр. |
1 |
5 |
8.6 |
8.60 |
-0.00 |
-0.00 |
| 24 |
15 пр. пр. |
2 |
4 |
10.1 |
10.10 |
0.00 |
0.00 |
Как видно из данных табл.3, статистическая закономерность имеет 100-ую доверительную вероятность, так как относительная погрешность равна нулю.
Связь между длиной и площадью водосбора притоков реки Шклея характеризуется уравнением
S=5,8273L0,4215,
а обратная связь можно описать уравнением (табл.4)
L=0,4358S0,9953.
Таблица 4
Взаимозависимости длины и площади водосбора притоков реки Шклея |
| № п/п |
Зависимость S=f(L) |
Зависимость L=f(S) |
| L, км |
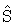 , км2 , км2 |
S, км2 |
 |
 , % , % |
S, км2 |
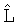 , км , км |
L, км |
 |
 , % , % |
| 3 |
2.9 |
6.5 |
9.1 |
-2.63 |
-40.46 |
6.5 |
2.9 |
2.8 |
0.09 |
3.10 |
| 6 |
3.6 |
10.1 |
10.0 |
0.10 |
0.99 |
10.1 |
3.6 |
4.4 |
-0.75 |
-20.83 |
| 11 |
3.8 |
11.9 |
10.2 |
1.67 |
14.03 |
11.9 |
3.8 |
5.1 |
-1.33 |
-35.00 |
| 14 |
4.0 |
11.9 |
10.5 |
1.45 |
12.18 |
11.9 |
4.0 |
5.1 |
-1.13 |
-28.25 |
| 16 |
5.1 |
15.2 |
11.6 |
3.62 |
23.82 |
15.2 |
5.1 |
6.5 |
-1.44 |
-28.24 |
| 18 |
2.2 |
8.3 |
8.1 |
0.18 |
2.17 |
8.3 |
2.2 |
3.6 |
-1.38 |
-62.73 |
| 21 |
9.1 |
16.6 |
14.8 |
1.82 |
10.96 |
16.6 |
9.1 |
7.1 |
1.96 |
21.54 |
| 22 |
6.9 |
8.6 |
13.2 |
-4.55 |
-52.91 |
8.6 |
6.9 |
3.7 |
3.19 |
46.23 |
| 24 |
5.3 |
10.1 |
11.8 |
-1.67 |
-16.53 |
10.1 |
5.3 |
4.4 |
0.95 |
17.92 |
Сопоставление показывает, что формула типа S=f(L) точнее формулы зависимости типа L=f(S). При этом приведенная в прототипе усредненная зависимость 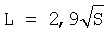 оказывается вообще неприемлемой. оказывается вообще неприемлемой.
Предлагаемый способ может быть применен к любой речной системе, то есть реке с притоками. Но особенно она эффективна применительно к малым рекам, имеющим разветвленную сеть притоков первого порядка, которые на территории Республики Марий Эл еще во многом сохранились в естественном виде. Этот способ эффективен также при использовании до проведения тщательных полевых исследований, так как позволяет оценить потребность в затратах на исследования, спрогнозировать ожидаемую эффективность по водным ресурсам и рациональному природопользованию с учетом выявленных и уточненных на основе проведенных полевых измерений значений длины и площади водосбора всех притоков речной сети.
Формула изобретения
1. Способ измерения площади водосбора равнинной реки по длинам притоков, включающий натурное измерение длин притоков реки, измерения площади водосбора притоков при помощи аэрофотосъемки, использование среднестатистической формулы 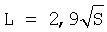 , где L – длина реки (притока), км, S – площадь водосбора притока или всей реки, км2, для описания связи между площадью бассейна и длиной реки по измеренным притокам реки, а по неизмеренным притокам вычисление расчетного значения площади водосбора каждого неизмеренного притока выполняется по эмпирической формуле S=f(L), причем все притоки реки располагают отдельно по убыванию длины и отдельно по убыванию площади водосбора, присваивают ранги каждому притоку, начиная с единицы, после этого в этих ранговых распределениях выделяют группы притоков по измеренным и неизмеренным значениям длины притоков или площади водосборов этих же притоков, по измеренным притокам реки по их длине и площади водосбора выявляют закономерности распределения отдельно по убыванию длины притоков и отдельно по убыванию площади водосбора притоков, а затем по найденным закономерностям распределения с использованием указанной эмпирической формулы вычисляют ориентировочные значения площади водосбора неизмеренных притоков. , где L – длина реки (притока), км, S – площадь водосбора притока или всей реки, км2, для описания связи между площадью бассейна и длиной реки по измеренным притокам реки, а по неизмеренным притокам вычисление расчетного значения площади водосбора каждого неизмеренного притока выполняется по эмпирической формуле S=f(L), причем все притоки реки располагают отдельно по убыванию длины и отдельно по убыванию площади водосбора, присваивают ранги каждому притоку, начиная с единицы, после этого в этих ранговых распределениях выделяют группы притоков по измеренным и неизмеренным значениям длины притоков или площади водосборов этих же притоков, по измеренным притокам реки по их длине и площади водосбора выявляют закономерности распределения отдельно по убыванию длины притоков и отдельно по убыванию площади водосбора притоков, а затем по найденным закономерностям распределения с использованием указанной эмпирической формулы вычисляют ориентировочные значения площади водосбора неизмеренных притоков.
2. Способ измерения площади водосбора равнинной реки по длинам притоков по п.1, отличающийся тем, что ранги присваивают от единицы и более целыми числами в порядке убывания длины притока и площади его водосбора по всем притокам, содержащим как неизмеренные, так и измеренные по карте или в натуре значения параметров длины и площади.
3. Способ измерения площади водосбора равнинной реки по длинам притоков по п.1, отличающийся тем, что группу неизмеренных притоков разделяют на подгруппы: во-первых, притоки с измеренными длинами, но с неизмеренными значениями площади водосбора, во-вторых, притоки, у которых известны только ранговые расположения по реке среди измеренных притоков, в-третьих, притоки, у которых известны значения площади водосбора, но неизвестны значения длины, причем все измеренные и неизмеренные притоки дополнительно измеряют по картам, при помощи аэрофотосъемки или другими известными способами для уточнения исходных данных.
4. Способ измерения площади водосбора равнинной реки по длинам притоков по п.1, отличающийся тем, что из всех измеренных и неизмеренных притоков в процессе ранжирования исключаются притоки, у которых по различным причинам отсутствует водоток, а также притоки более высоких порядков Р.Хортона, то есть для статистического моделирования оставляются действующие притоки первого и второго порядков при условии, что значения длины и площади водосбора притоков второго порядка малозначимо отличаются от наибольших значений длины и площади водосбора наибольшего притока первого порядка.
5. Способ измерения площади водосбора равнинной реки по длинам притоков по п.1 или 4, отличающийся тем, что по длине и площади водосбора измеренных и уточненных притоков реки выявляют закономерности распределения отдельно по убыванию длины и отдельно по убыванию площади водосбора по формуле 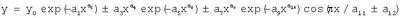 , ,
где y – показатели притока реки (длина притока L, км, или площадь водосбора притока S, км2),
y0 – теоретически возможное максимальное значение показателя для данной речной сети,
х – ранг значений длины притока rL или ранг значений площади водосбора притока rS,
а1…а12 – параметры статистической модели, причем при значениях некоторых из них, равных нулю или единице, происходит изменение структуры уравнения (например, чаще всего а6=1, а10=1, a8=0 или a9=0).
6. Способ измерения площади водосбора равнинной реки по длинам притоков по п.1 или 4, отличающийся тем, что для неизмеренных притоков используют эмпирическую формулу S=f(L), полученную по значениям длины и площади водосбора измеренных притоков, которую определяют по формуле устойчивого закона аллометрического роста 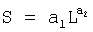 , где S – площадь водосбора притока, км2, L – длина водотока, км, а1, а2 – параметры статистической модели (причем в частных случаях может быть а2=0,5). , где S – площадь водосбора притока, км2, L – длина водотока, км, а1, а2 – параметры статистической модели (причем в частных случаях может быть а2=0,5).
7. Способ измерения площади водосбора равнинной реки по длинам притоков по п.1 или 4, отличающийся тем, что по найденным закономерностям распределения длины и площади водосбора у измеренных и уточненных после экспериментальных измерений группы притоков реки, а также по полученной эмпирической формуле сопоставленных расчетных значений принимают значения площади водосбора для неизмеренных притоков.
8. Способ измерения площади водосбора равнинной реки по длинам притоков по п.1 или 4, отличающийся тем, что для окончательного выяснения достоверных значений площади водосбора у неизмеренных притоков и уточнения значений длины и площади водосбора у измеренных притоков дополнительно проводят полевые исследования, причем по отклонениям от ранее проведенных полевых исследований судят о динамике длины и площади водосборов отдельных притоков реки.
MM4A – Досрочное прекращение действия патента СССР или патента Российской Федерации на изобретение из-за неуплаты в установленный срок пошлины за поддержание патента в силе
Дата прекращения действия патента: 25.12.2006
Извещение опубликовано: 10.09.2008 БИ: 25/2008
|
|