Патент на изобретение №2155935
|
||||||||||||||||||||||||||
(54) СПОСОБ БЕСКОНТАКТНОГО ВЫВЕШИВАНИЯ СВЕРХПРОВОДНИКОВ
(57) Реферат: Изобретение относится к области электротехники, а точнее к устройствам с использованием сверхпроводников. Предлагается способ бесконтактного вывешивания в магнитном поле сверхпроводников, имеющих малые значения нижнего критического поля. Изобретение направлено на увеличение удерживающей силы. Сущность изобретения заключается в том, что в левитирующем теле формируется пятно магнитного потока в виде вихрей Абрикосова, при этом ее магнитный момент взаимодействует с полем магнитной системы. 3 ил. Изобретение относится к области электротехники, а точнее к устройствам с использованием сверхпроводников. Известен способ бесконтактного удержания сверхпроводников, основанный на их идеальном диамагнетизме (эффект Мейснера) [1], при этом сверхпроводящее тело располагается над магнитом, поле которого, если оно меньше первого критического Bк1, будет выталкиваться из его объема, тем самым создавая силу, удерживающую сверхпроводник в бесконтактном положении. При этом величина поля магнита не должна превышать Вк1 сверхпроводника, и удельная удерживающая сила равна: 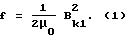 Для реализации этого метода необходимы сверхпроводники с большим значением нижнего критического поля Bк1. В устройствах используются ниобий и его сплавы с Bк1 порядка 0,1 Тл, работающие при температуре жидкого гелия, что в большинстве случаев экономически не целесообразно. Однако этот способ не позволяет получить большие значения удерживающей силы, в случае использования сверхпроводников с малыми значениями нижнего критического поля, к которым относятся высокотемпературные сверхпроводники с Вк1 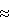 0,02 Тл, применение которых возможно при температурах жидкого азота.
Изобретение направлено на увеличение удерживающей силы.
Это достигается тем, что в левитирующем теле формируют локальную область с магнитным потоком в виде вихрей Абрикосова, при этом ее магнитный момент взаимодействует с полем магнитной системы, создающей эту область.
Изобретение поясняется чертежами. На фиг. 1 показано расположение левитирующего тела 1 в виде пластинки из сверхпроводника, относительно полюсов магнитной системы 2, создающий поле В. На фиг. 2 показан изгиб вихря Абрикосова 3 на угол 0,02 Тл, применение которых возможно при температурах жидкого азота.
Изобретение направлено на увеличение удерживающей силы.
Это достигается тем, что в левитирующем теле формируют локальную область с магнитным потоком в виде вихрей Абрикосова, при этом ее магнитный момент взаимодействует с полем магнитной системы, создающей эту область.
Изобретение поясняется чертежами. На фиг. 1 показано расположение левитирующего тела 1 в виде пластинки из сверхпроводника, относительно полюсов магнитной системы 2, создающий поле В. На фиг. 2 показан изгиб вихря Абрикосова 3 на угол  при смещении левитирующего тела 1 на расстояние при смещении левитирующего тела 1 на расстояние  z. На фиг. 3 показаны результаты экспериментальной проверки предлагаемого способа – зависимость силы взаимодействия F левитирующего тела с магнитной системой от смещения z при поле В = 0.13 Тл.
Сущность предлагаемого способа заключается в следующем. Сверхпроводящее тело 1 (фиг.1), например, в виде пластинки размещается между полюсами магнитной системы 2, поле которой величиной B>Bк1 создает в объеме тела область, где оно существует в виде вихрей Абрикосова [6]. При смещении пластины вниз под действием силы тяжести на расстояние z. На фиг. 3 показаны результаты экспериментальной проверки предлагаемого способа – зависимость силы взаимодействия F левитирующего тела с магнитной системой от смещения z при поле В = 0.13 Тл.
Сущность предлагаемого способа заключается в следующем. Сверхпроводящее тело 1 (фиг.1), например, в виде пластинки размещается между полюсами магнитной системы 2, поле которой величиной B>Bк1 создает в объеме тела область, где оно существует в виде вихрей Абрикосова [6]. При смещении пластины вниз под действием силы тяжести на расстояние  z, запиннингованные вихри, смещающиеся вместе с кристаллической решеткой, будут изгибаться, оставаясь закрепленными. На фиг.2 показан изгиб вихря Абрикосова 3 при смещении левитирующего тела 1. При этом на единичный вихрь со стороны внешнего магнитного поля будет действовать момент силы [2] z, запиннингованные вихри, смещающиеся вместе с кристаллической решеткой, будут изгибаться, оставаясь закрепленными. На фиг.2 показан изгиб вихря Абрикосова 3 при смещении левитирующего тела 1. При этом на единичный вихрь со стороны внешнего магнитного поля будет действовать момент силы [2]M = pmBSin  , (2) , (2)а приложенная к нему сила будет равна: f = pmBSin  /l /l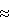 2pmB 2pmB z/d2, (3) z/d2, (3)где pm – магнитный момент вихря,  – угол между направлением магнитного момента изогнутого вихря и полем, l – длина вихря, приближенно равная толщине пластины d.
В целом же на пятно магнитного потока будет действовать сила F= N0f, где N0= – угол между направлением магнитного момента изогнутого вихря и полем, l – длина вихря, приближенно равная толщине пластины d.
В целом же на пятно магнитного потока будет действовать сила F= N0f, где N0= 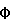 / /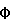 0 – число вихрей, 0 – число вихрей, 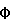 – магнитный поток, заключенный в объеме пятна, – магнитный поток, заключенный в объеме пятна, 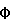 0 – квант магнитного потока.
Если вес тела меньше силы пиннинга всех вихрей, то это тело будет бесконтактно подвешено между полюсами магнита.
Сила пиннинга определяется как 0 – квант магнитного потока.
Если вес тела меньше силы пиннинга всех вихрей, то это тело будет бесконтактно подвешено между полюсами магнита.
Сила пиннинга определяется какFп=F0  Vв, (4) Vв, (4)где F0 – объемная сила пиннинга, параметр, характеризующий данный сверхпроводник, который определяется кристаллической структурой и величиной магнитного поля (количеством вихрей); Vв – объем области, где существуют вихри. Если вес тела P =   Vт Vт g (( g (( – плотность сверхпроводника, Vт – объем тела, g – ускорение свободного падения), то условием левитации будет Fп – плотность сверхпроводника, Vт – объем тела, g – ускорение свободного падения), то условием левитации будет Fп 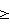 P, т.е.
F0 P, т.е.
F0 V V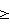   Vт Vт g. (5) g. (5)Принимая, например, что объем Vв занимает половину Vт, получаем F0 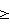 2 2  g. (6) g. (6)Так как F0= jkВ, где jk – критический ток, то (6) можно представить в виде jkB 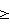 2 2  g. (7) g. (7)Характерные значения p для высокотемпературных сверхпроводников (ВТСП) 5000- 6000 кг/м3, тогда F0 должно превышать значение (1-1,2)  105 H/м3. Это значит, что при поле 0,1 Тл критический ток сверхпроводника должен быть порядка 106 А/м2. В настоящее время известны ВТСП, имеющие значения критического тока 108 – 109 А/м2 [3-4], что позволяет выполнить условие левитации.
Для проверки предлагаемого способа на установке, описанной в [5], были проведены эксперименты по бесконтактному вывешиванию пробного тела в виде пластинки с размерами (20х5х1,5)мм3 и массой 0,78 105 H/м3. Это значит, что при поле 0,1 Тл критический ток сверхпроводника должен быть порядка 106 А/м2. В настоящее время известны ВТСП, имеющие значения критического тока 108 – 109 А/м2 [3-4], что позволяет выполнить условие левитации.
Для проверки предлагаемого способа на установке, описанной в [5], были проведены эксперименты по бесконтактному вывешиванию пробного тела в виде пластинки с размерами (20х5х1,5)мм3 и массой 0,78 10-3 кг из сверхпроводника Y-Ba-Cu-O, имеющего следующие параметры: начало и конец сверхпроводящего перехода соответственно 93 и 82К, плотность 5,2 г/см3. Эксперимент проводился в газообразном азоте при температуре 10-3 кг из сверхпроводника Y-Ba-Cu-O, имеющего следующие параметры: начало и конец сверхпроводящего перехода соответственно 93 и 82К, плотность 5,2 г/см3. Эксперимент проводился в газообразном азоте при температуре 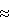 78 К. Была обнаружена устойчивая левитация тела в поле 0.13 Тл.
Кроме того проведены измерения силы F, возникающей при смещении сверхпроводящего тела в рассматриваемой выше ситуации. Полученная зависимость силы взаимодействия сверхпроводника с магнитной системой F от смещения z при значении поля В= 0,13 Тл представлена на фиг.3. Как видно, с ростом смещения сила F быстро возрастает и при z > 0,7 мм достигает значения 19 78 К. Была обнаружена устойчивая левитация тела в поле 0.13 Тл.
Кроме того проведены измерения силы F, возникающей при смещении сверхпроводящего тела в рассматриваемой выше ситуации. Полученная зависимость силы взаимодействия сверхпроводника с магнитной системой F от смещения z при значении поля В= 0,13 Тл представлена на фиг.3. Как видно, с ростом смещения сила F быстро возрастает и при z > 0,7 мм достигает значения 19 10-3Н. Такая величина силы позволяет выполнить условие левитации для тела массой 10-3Н. Такая величина силы позволяет выполнить условие левитации для тела массой  1,9 1,9 10-3 кг. Таким образом, удерживающая сила в данной экспериментальной ситуации превышает вес тела в 2,4 раза.
Оценим величину удерживающей силы для используемого пробного тела, вывешиваемого с помощью известного (основанного на эффекте Мейснера) способа. Из формулы (1) максимально возможная удерживающая сила f, действующая на единицу поверхности сверхпроводника, для Bk1= 0.02 Тл равна 0.9 H/м2. При площади, большей грани пластинки 1 10-3 кг. Таким образом, удерживающая сила в данной экспериментальной ситуации превышает вес тела в 2,4 раза.
Оценим величину удерживающей силы для используемого пробного тела, вывешиваемого с помощью известного (основанного на эффекте Мейснера) способа. Из формулы (1) максимально возможная удерживающая сила f, действующая на единицу поверхности сверхпроводника, для Bk1= 0.02 Тл равна 0.9 H/м2. При площади, большей грани пластинки 1  10-4 м2, получаем величину удерживающей силы 0.9 10-4 м2, получаем величину удерживающей силы 0.9  10-4H, что меньше, чем в предлагаемом нами способе.
Источники информации 10-4H, что меньше, чем в предлагаемом нами способе.
Источники информации1. Ковалев В.П. Опоры и подвесы гироскопических устройств. – М.: Машиностроение, 1970. – 286 с. 2. Иродов И. Е. Основные законы электромагнетизма. – М.: Высшая школа, 1983.- 279 с. 6. Чечерников В.И. Магнитные измерения, Издательство Московского Университета, 1963, стр. 24. Формула изобретения
РИСУНКИ
MM4A Досрочное прекращение действия патента Российской Федерации на изобретение из-за неуплаты в установленный срок пошлины за поддержание патента в силе
Дата прекращения действия патента: 27.10.2000
Номер и год публикации бюллетеня: 28-2002
Извещение опубликовано: 10.10.2002
|
||||||||||||||||||||||||||
