|
|
(21), (22) Заявка: 2004126302/28, 30.08.2004
(24) Дата начала отсчета срока действия патента:
30.08.2004
(45) Опубликовано: 27.03.2006
(56) Список документов, цитированных в отчете о
поиске:
ТРОФИМОВА Т.И. КУРС ФИЗИКИ. М.: Высшая школа, 2000, 542 с. SU 1717817 А1, 07.03.1992. SU 1693488 A1, 23.11.1991. SU 1405623 A1, 30.08.1990.
Адрес для переписки:
350044, г.Краснодар, ул. Калинина, 13, КГАУ, ПИО
|
(72) Автор(ы):
Александров Борис Леонтьевич (RU),
Родченко Мила Борисовна (RU)
(73) Патентообладатель(и):
Федеральное государственное образовательное учреждение высшего профессианального образования Кубанский Государственный аграрный университет (RU)
|
(54) СПОСОБ ОЦЕНКИ РАДИУСОВ АТОМОВ ХИМИЧЕСКИХ ЭЛЕМЕНТОВ В РАЗЛИЧНОМ ЭНЕРГЕТИЧЕСКОМ СОСТОЯНИИ
(57) Реферат:
Технический результат изобретения заключается в повышении достоверности оценки радиусов атомов химических элементов. Сущность: определяют физическими методами заряд электрона, диэлектрическую проницаемость вакуума, спектр излучения фотонов атомов данного элемента, потенциал ионизации атома. С учетом соотношения величины силы ионизации и кулоновской силы притяжения электрона к ядру по предлагаемой расчетной формуле проводят оценку радиусов атомов химических элементов в различном энергетическом состоянии. 6 табл.
Изобретение относится к химической промышленности, в частности к измерениям размеров атомов и ионов химических элементов.
Известен способ оценки радиусов атомов химических элементов через величину объемной плотности вещества из этих элементов. Для этого по известной величине объемной плотности вещества из данного химического элемента, его молярной массе, межатомной пористости на основании предполагаемого координационного числа и типа кристаллической решетки, с учетом числа Авогадро (NA=6,0220·1023 атомов/моль_) определяется радиус атома по формуле
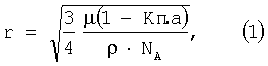
где  – объемная плотность вещества – объемная плотность вещества 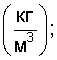  – молярная масса – молярная масса 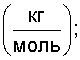 Кп.а – межатомная пористость в долях единицы. Кп.а – межатомная пористость в долях единицы.
Расчеты радиусов атомов по многим химическим элементам, выполненные разными авторами (Полинг, Мелвин и Хьюз, Белов и Бокию) с учетом принятых ими координационных чисел представлены Гороновским И.Т., Назаренко Ю.П., Некряч Е.Ф. в «Кратком справочнике по химии». Пятое издание. Киев, Наукова Думка, 1987 г., 830 с.
Недостатком этого способа является отсутствие данных о плотностях и типах кристаллических структур, т.е. достоверной оценки параметра Кп.а, веществ из различных химических элементов в различном энергетическом состоянии.
Также известен способ оценки радиуса атомов химических элементов путем определения физическими методами заряда электрона, диэлектрической проницаемости вакуума и учета их при определении радиуса атома по формуле Н.Бора на основании модели атома Э.Резерфорда (Трофимова Т.И. Курс физики. Издание шестое. М: Высшая школа, 2000 г., 542 с.)
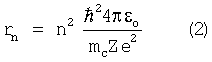
где n=1, 2, 3,… – главное квантовое число, принимающее целочисленные значения от 1 до  ; me – масса электрона; e – заряд электрона; Z – число протонов в ядре атома; ; me – масса электрона; e – заряд электрона; Z – число протонов в ядре атома;
 o – электрическая постоянная или диэлектрическая проницаемость вакуума; o – электрическая постоянная или диэлектрическая проницаемость вакуума;
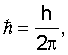 здесь h – постоянная Планка. здесь h – постоянная Планка.
Из выражения (2) следует, что радиусы орбит электронов, т.е. радиусы атомов, растут пропорционально квадратам целых чисел. Для атома водорода (Z=1) радиус первой орбиты электрона при n=1, называемый первым боровским радиусом, равен 0,528·10-10 м.
Недостатком этого технического решения является резкое возрастание размеров радиусов атомов химических элементов при увеличении параметра n, причем при n= r= r= , что не имеет физического смысла. В связи с этим, как правило, оперируют величинами n=1÷7. , что не имеет физического смысла. В связи с этим, как правило, оперируют величинами n=1÷7.
Кроме того, в выражении (2) через величину Z принимается условие влияния на валентный электрон всего заряда ядра без учета распределения энергии взаимодействия заряда ядра между всеми электронами атома и наличия экранирующего влияния на каждый электрон атома всех остальных его электронов. Поэтому выражение (2) в действительности используется только для расчета радиуса атома водорода при n=1÷7 и не используется для расчета радиусов атомов других химических элементов.
Техническим решением задачи является получение достоверной информации о величине радиусов атомов химических элементов в различном энергетическом состоянии.
Поставленная задача достигается тем, что в способе оценки радиусов атомов химических элементов путем определения физическими методами заряда электрона, диэлектрической проницаемости вакуума и учета их при определении радиуса атома определяют спектр излучения фотонов данного элемента, скорость излучения фотонов, потенциал ионизации ( ион) атома, отношение силы ионизации атома к силе кулоновского взаимодействия электрона с ядром и осуществляют оценку радиуса атома в различном его энергетическом состоянии для любой частоты излучаемого фотона по формуле: ион) атома, отношение силы ионизации атома к силе кулоновского взаимодействия электрона с ядром и осуществляют оценку радиуса атома в различном его энергетическом состоянии для любой частоты излучаемого фотона по формуле:
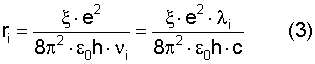
где 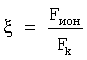 – отношение силы ионизации атома (Fион) к силе кулоновского притяжения (Fk) электрона к ядру из расчета одного протона в ядре, независимо от заряда ядра; e – заряд электрона (e=1,6·10-19 Кл.); – отношение силы ионизации атома (Fион) к силе кулоновского притяжения (Fk) электрона к ядру из расчета одного протона в ядре, независимо от заряда ядра; e – заряд электрона (e=1,6·10-19 Кл.);  0 – электрическая постоянная 0 – электрическая постоянная 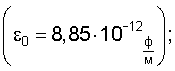 h – постоянная Планка (h=6,626·10-34 Дж·с); h – постоянная Планка (h=6,626·10-34 Дж·с);  i, i,  I – частота и длина волны испускаемого атомом фотона в спектре излучения; с – скорость света (c=2,997·108 м/с). I – частота и длина волны испускаемого атомом фотона в спектре излучения; с – скорость света (c=2,997·108 м/с).
В модели атома Э.Резерфорда, принятой за основу H.Бором, сила кулоновского взаимодействия электрона с ядром определяется величиной всего заряда ядра, т.е. Z·е. В действительности, в многоэлектронном атоме необходимо определять взаимодействие валентного электрона не только с ядром, но и с каждым (Z-1) электроном и определять равнодействующую силу взаимодействия, которая будет равна векторной сумме всех элементарных сил взаимодействия электрона со всеми зарядами электронов и ядра атома. Провести такой расчет результирующей силы без знания расположения всех электронов атома невозможно. Однако оценить эту результирующую силу можно по величине его потенциала ионизации ( ион). ион).
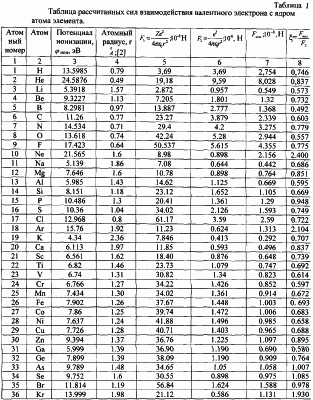
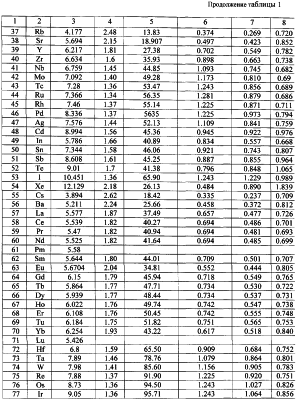
В таблице 1 с использованием величин потенциалов ионизации первых электронов атомов и их радиусов по данным Радциг А.А. и Шустрякова В.М. «Ионизация атомов и молекул». (Физические величины. Справочник. Под редакцией Григорьева И.С., Мейлихова Е.З. – М.: Энергоатомиздат, 1991 г., 1232 с.) представлены расчеты сил взаимодействия электрона с ядром в предположении влияния заряда ядра (сила F1) только одного протона ядра (сила F2) и сила, рассчитанная через величину потенциала ионизации (Fион). Расчет этой силы проводился по формуле:
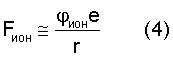
здесь  ион – потенциал ионизации атома; e – заряд электрона; r – радиус вращения электрона. ион – потенциал ионизации атома; e – заряд электрона; r – радиус вращения электрона.
Как видно из таблицы №1, 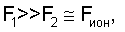 поэтому проведено сравнение величин F2 и Fион в виде отношения поэтому проведено сравнение величин F2 и Fион в виде отношения 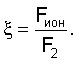 Анализ показывает, что для большинства химических элементов Анализ показывает, что для большинства химических элементов 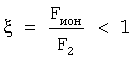 за исключением инертных газов. С увеличением количества электронов на последней орбитале за исключением инертных газов. С увеличением количества электронов на последней орбитале  несколько увеличивается с несколько увеличивается с 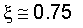 до 1÷2.4, причем максимально для легкого газа (Ne) и постепенно снижается до 1 для самого тяжелого инертного газа (Rn) (табл.1). до 1÷2.4, причем максимально для легкого газа (Ne) и постепенно снижается до 1 для самого тяжелого инертного газа (Rn) (табл.1).
Таким образом, для большинства элементов в расчетах силы взаимодействия электрона с ядром можно принять параметр 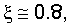 т.е. т.е.
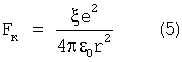
либо использовать конкретные значения  по таблице 1. по таблице 1.
Для обоснования выражения (3) рассмотрим причину вращения электрона по орбите.
Так как электрон вращается по орбите, то его движение должно характеризоваться вращающим моментом силы:
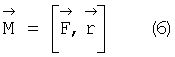
На первый взгляд представляется, что такой силой является кулоновская сила притяжения электрона ядром. Однако эта сила совпадает по направлению с радиус-вектором и их векторное произведение 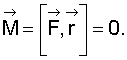
Принято считать, что кулоновская сила взаимодействия электрона и ядра создает центробежную силу
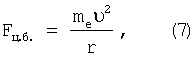
но и она совпадает по направлению с радиус-вектором и, следовательно, 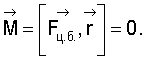
В связи с этим воспользуемся моментом количества движения электрона и найдем выражение вращающего момента как
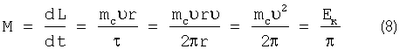
Здесь  – период вращения электрона вокруг ядра – период вращения электрона вокруг ядра 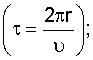 Ек – кинетическая энергия поступательного движения электрона по орбите, L – момент импульса электрона; me – масса электрона; d – скорость вращения электрона по орбите с радиусом r. Ек – кинетическая энергия поступательного движения электрона по орбите, L – момент импульса электрона; me – масса электрона; d – скорость вращения электрона по орбите с радиусом r.
Из последнего выражения видно, что момент импульса формирует в течение каждого периода обращения электрона вокруг ядра вращающий момент силы, который равен кинетической энергии (Eк) электрона, поделенной на параметр  . Важным здесь является тот факт, что вращающий момент определяется кинетической энергией и, следовательно, измеряется в Джоулях (Дж). За счет чего же все-таки появляется вращающий момент, если кулоновская и центробежная силы не могут его создать? . Важным здесь является тот факт, что вращающий момент определяется кинетической энергией и, следовательно, измеряется в Джоулях (Дж). За счет чего же все-таки появляется вращающий момент, если кулоновская и центробежная силы не могут его создать?
В соответствии с концепцией наличия фотонного электромагнитного поля вокруг электронов и нуклонов ядра атома за счет вращающихся вокруг них по своим орбитам фотонов (Александров Б.Л., Родченко М.Б., Александров А.Б. «Роль фотонов в физических и химических явлениях», Краснодар, ГУП «Печатный двор Кубани», 2002 г., 543 с.) остается предположить, что вращающий момент движения электрона по орбите создается в результате излучения фотона и равен энергии фотона
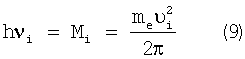
Воспользуемся известным равенством кулоновской и центробежной сил электрона атома с учетом выражения (5)
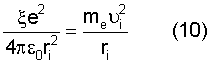
откуда 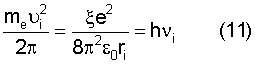
и тогда 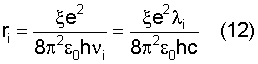
здесь  i – длина волны излучаемого i-го фотона; с – скорость света; e – заряд электрона; i – длина волны излучаемого i-го фотона; с – скорость света; e – заряд электрона;  0 – электрическая постоянная; 0 – электрическая постоянная;  i – скорость вращения электрона по орбите с радиусом ri; mi – масса электрона; i – скорость вращения электрона по орбите с радиусом ri; mi – масса электрона;  i – частота излучения i-го фотона i – частота излучения i-го фотона
Новизна заявляемого способа заключается в том, что наряду с известными физическими параметрами – величина заряда электрона, диэлектрическая проницаемость вакуума – учитываются величины длин волн (частот) всего спектра излучаемых фотонов, определяющих весь энергетический диапазон электрона атома конкретного химического элемента или его иона, скорость излучаемых фотонов, потенциал ионизации атома этого элемента и отношение силы ионизации атома к силе кулоновского взаимодействия электрона с ядром. В результате такого подхода обеспечивается объективная оценка радиуса атома химического элемента во всем диапазоне его энергетического состояния.
Заявленный способ обладает изобретательским уровнем, поскольку из данных научно-технической и патентной литературы не известна аналогичная заявляемой совокупность признаков, обеспеспечивающая достижение поставленной задачи.
Изобретение нашло применение при оценке радиусов атомов химических элементов во всем диапазоне их энергетического состояния, возможно использование его в промышленности при необходимости учета радиусов атомов и ионов в их широком диапазоне энергетического состояния при различных химических процессах. С учетом вышеизложенного можно судить о промышленной применимости предложения.
Для рассмотрения конкретных примеров осуществления способа оценки радиусов атомов химических элементов в различном энергетическом состоянии в таблице №2 представлены результаты расчетов радиусов атома ртути для всех длин волн излучаемых фотонов в соответствии с таблицами спектральных линий («Таблицы спектральных линий». Издание четвертое. М., Изд-во «Наука», Главная редакция физико-математической литературы, 1977 г., 800 с. Авторы: А.Н.Зайдель, В.К.Прокофьев, С.М.Райский, В.А.Славный, Е.Я.Шнейдер).
Оценка радиусов атома ртути для соответствующих длин волн излучаемых фотонов проводилась по формуле (12), причем использовалась величина
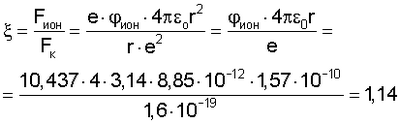
где  ион=10,437 эВ для атома ртути; r=1.57·10-10 м – радиус атома ртути по данным А.А.Радциг и В.М.Шустрякова «Ионизация атомов и молекул» (Физические величины. Справочник. Под редакцией И.С.Григорьева и Е.З.Мейлихова, М.: Энергоатомиздат, 1991 г., 1232 с.); e=1,6·10-19 Кл; ион=10,437 эВ для атома ртути; r=1.57·10-10 м – радиус атома ртути по данным А.А.Радциг и В.М.Шустрякова «Ионизация атомов и молекул» (Физические величины. Справочник. Под редакцией И.С.Григорьева и Е.З.Мейлихова, М.: Энергоатомиздат, 1991 г., 1232 с.); e=1,6·10-19 Кл; 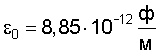
Для подтверждения достоверности полученных результатов оценки радиуса атома ртути в широком диапазоне энергетического состояния проведено их сравнение с расчетами радиусов атомов ртути через величины плотности при трех значениях температур по данным А.П.Бабичева «Плотность вещества» Физические величины. Справочник. Под редакцией И.С.Григорьева и Е.З.Мейлихова. М.: Энергоатомиздат, 1991 г, 1232 с.). Плотность ртути
при t=-38,9°C 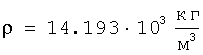 , ,
при t=0°C 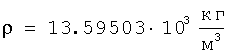 , ,
при t=800°C 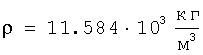 . .
Расчет радиуса атомов ртути по величине плотности при разных температурах проводился по формуле (1) с учетом того, что атомная масса ртути A=200,59 а.е.м. и, следовательно, мольная масса ртути 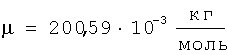 ; ; 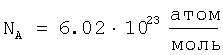 ; межатомная пористость Кп.а=0,4. ; межатомная пористость Кп.а=0,4.
| Таблица 2 |
| Расчет радиусов атома ртути во всем энергетическом диапазоне |
Длина волны излучения  i, Å i, Å |
Радиус атома, ri, Å |
Длина волны излучения  i, Å i, Å |
Радиус атома, ri, Å |
Длина волны излучения  i, Å i, Å |
Радиус атома, ri, Å |
Длина волны излучения  i, Å i, Å |
Радиус атома, ri, Å |
| 1 |
2 |
1 |
2 |
1 |
2 |
1 |
2 |
| 45122,04 |
9,4969 |
11206,0 |
2,3585 |
4991,5 |
1,0506 |
2803,47 |
0,5900 |
| 39283,61 |
8,2681 |
11176,8 |
2,3524 |
4916,07 |
1,0347 |
2799,76 |
0,5893 |
| 36303,03 |
7,6407 |
10715,5 |
2,2553 |
4890,27 |
1,0292 |
2759,71 |
0,5808 |
| 32148,06 |
6,7663 |
10432,0 |
2,1956 |
4827,1 |
1,0160 |
2752,78 |
0,5794 |
| 23253,07 |
4,8941 |
10423,5 |
2,1938 |
4358,33 |
0,9173 |
2699,51 |
0,5682 |
| 22493,28 |
4,7341 |
10359,5 |
2,1804 |
4347,49 |
0,9150 |
2698,83 |
0,5680 |
| 19700,17 |
4,1463 |
10333,0 |
2,1748 |
4343,63 |
0,9142 |
2655,13 |
0,5588 |
| 18130,38 |
3,8158 |
10298,2 |
2,1675 |
4339,22 |
0,9133 |
2653,68 |
0,5585 |
| 17436,18 |
3,6698 |
10229,6 |
2,1530 |
4108,05 |
0,8646 |
2652,04 |
0,5582 |
| 17329,41 |
3,6473 |
10139,79 |
2,1341 |
4077,83 |
0,8583 |
2625,19 |
0,5525 |
| 17213,20 |
3,6229 |
10129,7 |
2,1320 |
4046,56 |
0,8517 |
2603,15 |
0,5479 |
| 17206,15 |
3,6214 |
10121,2 |
2,1302 |
3906,37 |
0,8222 |
2576,29 |
0,5422 |
| 17198,67 |
3,6198 |
7728,82 |
1,6267 |
3801,66 |
0,8001 |
2536,52 |
0,5339 |
| 17116,75 |
3,6025 |
7091,86 |
1,4926 |
3704,17 |
0,7796 |
2534,76 |
0,5335 |
| 17109,93 |
3,6011 |
7081,9 |
1,4905 |
3701,44 |
0,7790 |
2483,82 |
0,5228 |
| 17072,79 |
3,5933 |
6907,46 |
1,4538 |
3663,28 |
0,7710 |
2482,71 |
0,5225 |
| 16942,00 |
3,5658 |
6716,43 |
1,4136 |
3662,88 |
0,7709 |
2482,00 |
0,5224 |
| 16933,27 |
3,5639 |
6234,4 |
1,3121 |
3654,84 |
0,7692 |
2464,06 |
0,5186 |
| 16920,16 |
3,5611 |
6072,72 |
1,2781 |
3650,15 |
0,7682 |
2399,73 |
0,5051 |
| 16881,48 |
3,5530 |
5871,97 |
1,2359 |
3341,48 |
0,7033 |
2399,35 |
0,5050 |
| 15295,82 |
3,2193 |
5859,25 |
1,2332 |
3144,48 |
0,6618 |
2379,99 |
0,5009 |
| 13950,55 |
2,9361 |
5803,78 |
1,2215 |
3135,76 |
0,6599 |
2378,32 |
0,5006 |
| 13673,51 |
2,8778 |
5790,66 |
1,2188 |
3131,84 |
0,6592 |
2374,02 |
0,4997 |
| 13570,21 |
2,8561 |
5789,66 |
1,2185 |
3131,55 |
0,6591 |
2352,48 |
0,4951 |
| 13505,58 |
2,8425 |
5769,60 |
1,2143 |
3125,67 |
0,6579 |
2345,43 |
0,4936 |
| 13468,38 |
2,8347 |
5675,86 |
1,1946 |
3027,49 |
0,6372 |
2323,20 |
0,4890 |
| 13426,57 |
2,8259 |
5549,63 |
1,1680 |
3025,61 |
0,6368 |
2302,06 |
0,4845 |
| 13209,95 |
2,7803 |
5460,73 |
1,1493 |
3023,48 |
0,6363 |
2002,0 |
0,4214 |
| 12071,7 |
2,5407 |
5384,63 |
1,1333 |
3021,50 |
0,6359 |
1972,94 |
0,4152 |
| 12020,0 |
2,5298 |
5354,05 |
1,1269 |
2967,28 |
0,6245 |
1849,50 |
0,3893 |
| 11977,3 |
2,5209 |
5290,74 |
1,1135 |
2925,41 |
0,6157 |
1832,6 |
0,3857 |
| 11769,1 |
2,4770 |
5218,9 |
1,0984 |
2893,59 |
0,6090 |
1775,68 |
0,3737 |
| 1168,7 |
2,4601 |
5137,94 |
1,0814 |
2856,94 |
0,6013 |
1774,9 |
0,3736 |
| 11491,7 |
2,4186 |
5120,63 |
1,0777 |
2847,83 |
0,5994 |
1250,59 |
0,1847 |
| 11372,5 |
2,3935 |
5102,71 |
1,0740 |
2806,77 |
0,5907 |
|
|
| 11287,4 |
2,3756 |
5025,64 |
1,0577 |
2804,43 |
0,5902 |
|
|
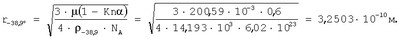
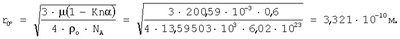
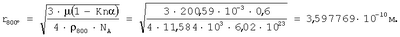
Рассчитанные величины радиусов атома ртути через величины плотности при трех значениях температур согласуются с количественной оценкой радиусов атома ртути в диапазоне длин волн 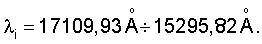
Для подтверждения возможности расчета радиуса атома по формуле (1) рассмотрим пример последовательности оценки параметров для определения радиуса атома через величину плотности вещества из алюминия. При t=20°C 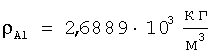 , атомная масса алюминия А=26,98154 а.е.м., т.е. масса одного моля равна , атомная масса алюминия А=26,98154 а.е.м., т.е. масса одного моля равна 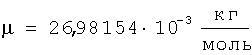 . В одном моле вещества содержится NA=6,022·1023 атомов и, следовательно, масса одного атома алюминия . В одном моле вещества содержится NA=6,022·1023 атомов и, следовательно, масса одного атома алюминия 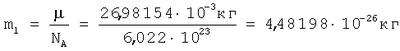 . В 1 м3 находится . В 1 м3 находится 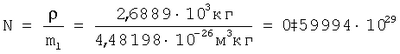 атомов алюминия. В результате объем, приходящийся на один атом в виде элементарного кубика атомов алюминия. В результате объем, приходящийся на один атом в виде элементарного кубика 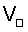 составит составит 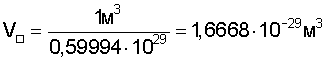 . Принимая условие, что атомы представляют собой сферические образования в виде шариков с определенным радиусом, а пространство между ними (межатомная пористость) свободно и занимает примерно 40% от общего объема, то объем атома в виде сферы составит V0=1,6668·10-29(1-0,4)=1,0000999·10-29 м3. Объем сферы . Принимая условие, что атомы представляют собой сферические образования в виде шариков с определенным радиусом, а пространство между ними (межатомная пористость) свободно и занимает примерно 40% от общего объема, то объем атома в виде сферы составит V0=1,6668·10-29(1-0,4)=1,0000999·10-29 м3. Объем сферы 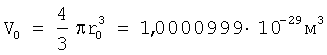 , следовательно, , следовательно, 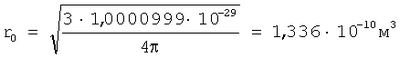 . Эта величина радиуса атома алюминия очень близка к данным других авторов (таблица 3). . Эта величина радиуса атома алюминия очень близка к данным других авторов (таблица 3).
По аналогии можно рассчитать радиусы атомов разных элементов, если известна их плотность и кристаллическая решетка, определяющая коэффициент межатомной пористости. Подобным способом для расчета радиусов атомов пользовались Полинг, Мелвин-Хьюз, Белов и Бокию [1], данные которых по многим элементам несколько расходятся, вероятно, ввиду принятия разного значения координационного числа (таблицы №3).
Однако провести расчеты радиусов атомов элементов через величину их объемной плотности в широком диапазоне температур (энергетического состояния) трудно ввиду отсутствия данных плотности и типов кристаллических структур в этих условиях.
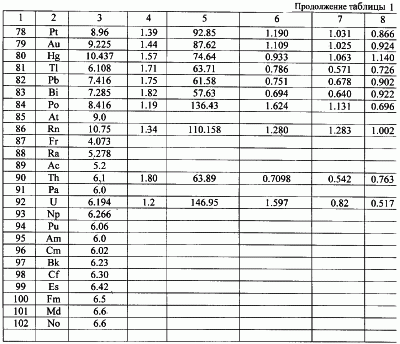
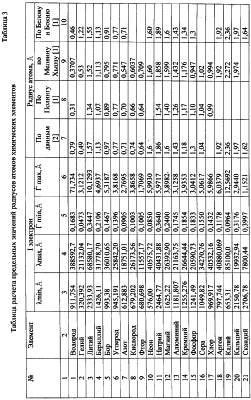
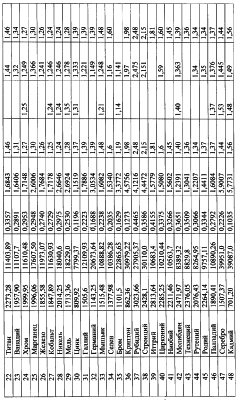
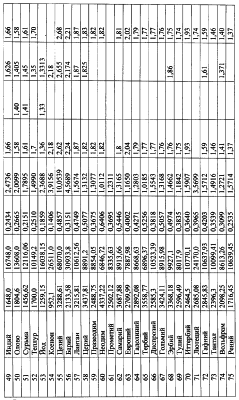
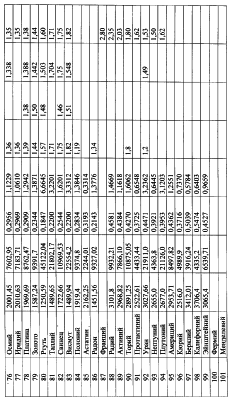
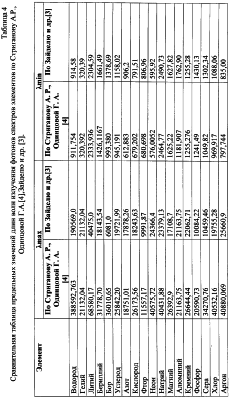
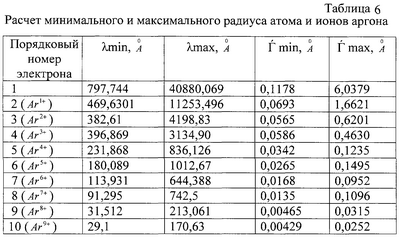
По формуле (12) осуществлена оценка минимального и максимального радиусов атомов всех химических элементов по величинам предельных значений длин волн излучения – поглощения фотонов по данным спектров этих химических элементов [3, 4], причем по первым 18 элементам данные спектров заимствованы из более позднего издания [4], в котором были представлены спектры только этих элементов. По остальным элементам использовались данные спектрального анализа из более раннего издания [3]. Результаты расчетов предельных значений радиусов атомов представлены в таблице №3. Анализ показывает, что примерно по 70% элементов данные разных авторов по радиусам атомов укладываются в диапазон (rmin-rmax), рассчитанным по предельным значениям длин волн излучения-поглощения фотонов, причем для первых 18 элементов, по которым использовалась более поздняя информация о спектрах элементов, получены и более объективные данные о предельных значениях радиусов атомов элементов. Наибольшее количество расхождений рассчитанных rmin-rmax по спектральным данным с данными радиусов атомов элементов других авторов (таблица 3) отмечено по элементам лантаноидам. Надо полагать, что данные спектрального анализа по этим и ряда других элементов не достаточно полные. Это подтверждается сопоставлением предельных значений длин волн в спектрах излучения-поглощения по ранним и более поздним публикациям спектров первых 18 элементов [3, 4] (таблица 4).
Представленные же в таблице 3 данные о радиусах атомов других авторов получены методом расчета через объемную плотность вещества при температуре, как правило, 20°С.
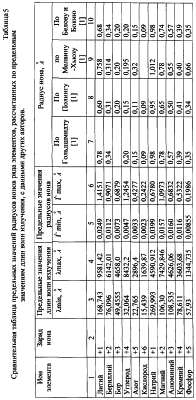
Наличие спектров излучения-поглощения фотонов для ионов различных элементов позволяет также осуществить по формуле (12) оценку их радиусов. Расчеты предельных значений радиусов rmin-rmax ионов представлены в таблице 5, причем по многим элементам, в частности по инертным газам, в литературе отсутствует информация о радиусах ионов, в то же время данные спектрального анализа [3] позволяют по той же формуле (12) провести их расчет. Для примера в таблице №6 для 9 ионов аргона даны расчеты предельных значений радиусов, которые закономерно уменьшаются с возрастанием заряда иона, т.е. с увеличением количества оторванных от атома электронов.
Таким образом, по формуле (12) можно рассчитать радиус любого атома и иона химического элемента во всем диапазоне энергий (длин волн) излучения-поглощения фотонов при наличии предварительно полученных результатов спектрального анализа этого элемента.
Список используемой литературы
1. Гороновский И.Т., Назаренко Ю.П., Некряч Е.Ф. Краткий справочник по химии. Пятое издание. Киев, Наукова Думка, 1987 г., 830 с.
2. Физические величины. Справочник. Под редакцией И.С.Григорьева, Е.3.Мейлихова. М, «Энергоатомиздит», 1991 г., 1232 с.
3. Таблицы спектральных линий. Издание четвертое. М., Изд-во «Наука», Главная редакция физико-математической литературы, 1977 г., 800 с.
4. Стриганов А.Р., Одинцова Г.А. Таблицы спектральных линий атомов и ионов. Справочник, М., «Энергоиздат», 1982 г., 312 с.
Формула изобретения
Способ оценки радиусов атомов химических элементов путем определения физическими методами заряда электрона, диэлектрической проницаемости вакуума и учет их при определении радиуса атома, отличающийся тем, что определяют спектр излучения фотонов атомов данного элемента, потенциал ионизации атома, отношение силы ионизации атома к силе кулоновского взаимодействия электрона с ядром и осуществляют оценку радиуса атома в различном его энергетическом состоянии для любой частоты излучаемого фотона по формуле
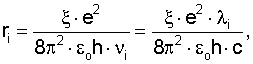
где 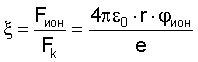 – отношение силы ионизации атома (Fион) к силе кулоновского взаимодействия электрона с ядром (Fк) из расчета одного протона в ядре, независимо от заряда ядра; e – заряд электрона; vi, – отношение силы ионизации атома (Fион) к силе кулоновского взаимодействия электрона с ядром (Fк) из расчета одного протона в ядре, независимо от заряда ядра; e – заряд электрона; vi,  i – частота и длина волны излучаемого фотона; i – частота и длина волны излучаемого фотона;  0 – электрическая постоянная или диэлектрическая проницаемость вакуума; с – скорость фотона; h – постоянная Планка; r – атомный радиус по справочным данным (рассчитанный по объемной плотности вещества). 0 – электрическая постоянная или диэлектрическая проницаемость вакуума; с – скорость фотона; h – постоянная Планка; r – атомный радиус по справочным данным (рассчитанный по объемной плотности вещества).
MM4A – Досрочное прекращение действия патента СССР или патента Российской Федерации на изобретение из-за неуплаты в установленный срок пошлины за поддержание патента в силе
Дата прекращения действия патента: 31.08.2006
Извещение опубликовано: 10.04.2008 БИ: 10/2008
|
|