Патент на изобретение №2271030
|
||||||||||||||||||||||||||
(54) СПОСОБ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПОЛОЖЕНИЯ ПРИВОДА
(57) Реферат:
Изобретение относится к системам автоматического позиционирования приводов, в частности может быть использовано для управления приводами радиолокационных станций. Технический результат – повышение точности регулирования. Для достижения данного результата сигнал ошибки положения привода определяют на основе разности скорости привода и скорости расчетной точки, для определения которой используются параметры системы автоматического регулирования положения привода, а также положение, скорость и ускорение объекта и точки наведения. При этом управление объектом осуществляют по трем координатам в полярной системе координат. В процессе формирования управляющих воздействий по каждой координате осуществляют в асинхронном режиме ввод координат цели от радиолокационной станции (РЛС) в ЭВМ. Затем на основе использования метода «скользящего окна» определяют сглаженные координаты и скорости движения цели. После этого осуществляют экстраполирование координат цели на текущий момент времени, которые переводят в полярную систему координат. Затем вводят в синхронном режиме от РЛС в ЭВМ координаты о текущем положении объекта, определяют составляющие скорости объекта и расчетной скорости точки наведения РЛС. На основе разницы расчетной и текущей скоростей наведения определяют величины сигналов ошибки наведения РЛС, которые подают на входы приводов азимута, угла места и дальности системы автоматического регулирования положения привода РЛС с заданным интервалом времени.
Область техники Данное техническое решение относится к регулирующим и управляющим системам общего назначения и цифровым (дискретным) вычислительным системам, а именно к системам управления приводами радиолокационной станции (РЛС) при измерении интегральных параметров воздушной обстановки. Уровень техники Аналогами заявляемого предполагаемого изобретения являются: СПОСОБ АВТОМАТИЧЕСКОЙ ЗАСТРОЙКИ МНОГОПАРАМЕТРИЧЕСКИХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ НА ОПТИМАЛЬНЫЕ УСЛОВИЯ (патент на изобретение RU 2189067 С2 от 10.09.2002, заявка 2000116797/09 от 23.06.2000 г.); СПОСОБ АДАПТИВНОЙ НАСТРОЙКИ МНОГОПАРАМЕТРИЧЕСКИХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ НА ОПТИМАЛЬНЫЕ УСЛОВИЯ (патент на изобретение RU 2189068 С2 от 10.09.2002, заявка 2000121221/09 от 23.06.2000 г.); СПОСОБ АДАПТИВНОЙ АВТОМАТИЧЕСКОЙ НАСТРОЙКИ МНОГОПАРАМЕТРИЧЕСКИХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ НА ОПТИМАЛЬНЫЕ УСЛОВИЯ (патент на изобретение RU 2189069 С2 от 10.09.2002, заявка 2000121222/09 от 07.08.2000 г.). Недостатком данных аналогов является несовместимость условия быстрого приведения объекта в заданную точку и одновременно условия точного сопровождения заданной точки с момента приведения объекта в заданную точку. Ближайшим аналогом (прототипом) заявляемого технического решения является СИСТЕМА ФУНКЦИОНАЛЬНО-ИМПУЛЬСНОГО УПРАВЛЕНИЯ СЕРВОПРИВОДОМ С НЕОПРЕДЕЛЕННОЙ ДИНАМИКОЙ (заявка на изобретение 93027855 А от 18.05.1993 г. МПК 6 G 05 В 13/00, Н 02 Р 5/00, дата публикации 27.09.1996 г.). В системе предлагается использовать три контура регулирования: по положению, по скорости и по ускорению. Микропроцессорный контроллер в каждом такте регулирования по ошибке положения объекта управления вычисляет ошибки по скорости и по ускорению и формирует функционально-импульсную последовательность. В пределах всего цикла регулирования в этой последовательности амплитуда и ширина импульсов модулируются пропорционально, а период следования импульсов – обратно пропорционально ошибке по положению и/или по скорости. В пределах же каждого такта регулирования амплитуда и ширина импульса многократно изменяются обратно пропорционально ошибке по ускорению. При этом скорости изменения амплитуды, ширины и периода следования импульсов в пределах всего цикла регулирования выбираются кратными, а минимальный временной сдвиг в пределах такта регулирования между двумя соседними импульсами выбирается из условия ортогональности этих сигналов. Сформированная таким образом функционально-импульсная последовательность подается на блок усилителей мощности, выход которого подключен к двигателю. Недостатком прототипа является трудность точного сопровождения заданной точки после приведения объекта в заданную точку при больших скоростях перемещения заданной точки. Сущность изобретения Для измерения интегральных параметров воздушной обстановки требуется решение задач поиска и сопровождения воздушного объекта станцией сопровождения цели (ССЦ). При этом в большинстве случаев необходимо автоматически управлять электромеханическими приводами антенны ССЦ. Эта задача сводится к вычислению управляющих воздействий (УВ), приводящих линию визирования антенны (ЛВА) ССЦ в точку цели и удерживающих луч локатора в точке цели. Обычно для вычисления УВ используются значения текущих рассогласований между координатами и скоростями цели и приводов. Значения рассогласований используются с поправочными коэффициентами. Коэффициенты определяются по контрольным примерам управления приводами в режиме «Регламент». Для простой задачи, например выведения луча локатора в заданную неподвижную точку, такой способ приемлем. Для задачи поиска и сопровождения движущейся цели такой способ неудобен. В разных режимах работы оптимальное по времени и точности управление требует разных коэффициентов. Поэтому в режиме «Регламент» нужно подобрать или компромиссные для всех случаев значения коэффициентов, или группы коэффициентов для разных режимов. Желательно при этом в режиме «Регламент» предусмотреть как можно больше ситуаций, которые потом могут встретиться в реальной работе. Целью данного изобретения является создание условий быстрого приведения объекта в заданную точку в пространстве и одновременно точного сопровождения этой точки. В данном алгоритме для вычисления УВ используются так называемые расчетные скорости и ускорения привода. Эти значения однозначно определяются дифференциальным уравнением движения привода. При этом задача управления приводами сводится к выполнению последовательности следующих шагов: – определяются характеристики привода; – вычисляются расчетные значения констант для алгоритма; – определяются координаты точки цели и объекта; – вычисляются расчетные значения переменных для алгоритма; – вычисляются управляющие воздействия. При таком подходе вместо подбора подходящих коэффициентов для вычисления рассогласований определяются постоянные уравнения движения. Эта задача сводится к измерению в общем случае трех параметров. Известный способ работы системы автоматического регулирования положения привода реализован на аппаратуре приема и реализации целеуказания, содержащей электронную вычислительную машину и блоки ввода и вывода дискретной информации по трем координатам в полярной системе координат управления приводом. Для достижения цели создания условий быстрого приведения объекта в заданную точку в пространстве и одновременно точного сопровождения этой точки в данном способе сигнал ошибки определяется по разности скорости привода и скорости фиктивной расчетной точки, для вычисления которой используются параметры системы регулирования, а также положение, скорость и ускорение объекта и точки наведения, управление объектом осуществляется по трем координатам в полярной системе координат и заключается в выполнении следующих шагов вычислительного алгоритма (управление по каждой координате выполняется одинаково): шаг 1 – ввод прямоугольных координат точки наведения (Хс Yc Hc) от радиолокационной станции (РЛС) в компьютер, данные поступают асинхронно, с темпом несколько секунд; шаг 2 – вычисление сглаженных координат (Xs Ys Hs) и скоростей (Vxs Vys Vhs) методом «скользящее окно»: Xcs=Xcs+Vxs dX=Хс-Xcs, dVx=dX/dT, Xcs=Xcs+Kk Vxs=Vxs+Kv где Xcs – сглаженная координата, Vxs – сглаженная скорость, Kk – коэффициент сглаживания координаты, Kv – коэффициент сглаживания скорости, dT – интервал времени между последними поступлениями координат; шаг 3 – экстраполирование координат на текущий момент времени (Xct, Yct, Hct): Xct=Xcs+Vxs где Xct – текущая координата, DT – длительность такта выдачи сигналов рассогласований (10 мс); шаг 4 – вычисление составляющих полярных координат (Bc Ec Dc) и скорости (VBc Vec VDc): Dg=sqrt(Xct Dc=sqrt(Dg+Hct Bc=atan(Yct/Xct), Ec=asin(Hct/Dc), VBc=(XctVys-YctVxs)/(Dg VEc=[Dg VDc=(Xct где Dg, Dc – горизонтальная и наклонная дальность, Bc, Ес – азимут и угол места, VBc, VEc, VDc – составляющие скорости по азимуту, углу места и дальности; шаг 5 – ввод текущих координат положения объекта (Вр Ер Dp) от РЛС в компьютер, данные поступают синхронно, с темпом DT (10 мс); шаг 6 – вычисление составляющих скорости объекта (VBp VEp VDp): VBp=(Bp-Bp1)/DT1, VEp=(Ep-Ep1)/DT1, VDp=(Dp-Dp1)/DT1, где Bp1, Ep1, Dp1 – азимут, угол места и дальность объекта во время на DT1 ранее текущего времени, DT1 – временной интервал измерения скорости объекта; шаг 7 – вычисление составляющих расчетной скорости точки наведения (VBP, VEP, VDP): VBP=sign(dBP) где VBc – текущая скорость точки цели, WBc – изменение скорости точки цели на интервале dT: WBc=(VBc-VBc1)/dT, где VBc1 – скорость точки цели во время на dT ранее текущего времени, WBP – расчетное ускорение привода по азимуту: WBP=KWP где KWP – коэффициент «запаса» по ускорению, WBmax – максимальное ускорение привода по азимуту: WBmax=VBmax/ТВэм, где ТВэм – электромеханическая постоянная времени привода по азимуту, VBmax – максимальная скорость привода по азимуту: VBmax=KB где KB – коэффициент усиления привода азимута, ABm – максимальное значение входного сигнала на привод азимута, dBP – рассогласование по азимуту объекта и точки цели: dBP=(Вс-Вр)+(VBc-VBp) sign(dBP) – знак рассогласования по азимуту объекта и точки цели, abs(dBP) – абсолютное значение рассогласования по азимуту объекта и точки цели; шаг 8 – вычисление сигналов ошибки (SOB, SOE, SOD): SOB=VBP-VBp, SOE=VEP-VEp, SOD=VBD-VDp, если полученное значение SOB по модулю превышает значение максимального входного сигнала ABm, принимается значение SOB, по модулю равное ABm; шаг 9 – выдача сигналов ошибки SOB, SOE, SOD на входные регистры привода азимута, привода угла места и привода дальности системы автоматического регулирования, данные выдаются с интервалом DT (10 мс). Пример варианта реализации заявляемого способа УСЛОВИЯ ЗАДАЧИ Приращения угла dB считаются положительными при вращении привода по часовой стрелке. Положительным значениям Сигналов Ошибки (СО) соответствует положительное ускорение, то есть при движении привода по часовой стрелке происходит разгон привода, а при движении против часовой стрелки – торможение. Максимальные значения скорости и ускорения привода имеют ограничения: |Vp| |Wp| Ускорение прямо пропорционально СО типа «скачек», максимальное значение ускорения достигается при воздействии максимального СО. ЗАДАЧА Требуется вывести привод, находящийся в точке Bt и вращающийся с угловой скоростью Vt, в заданную точку Вс, перемещающуюся с угловой скоростью Vc, за минимальное время, с учетом ограничений максимальных значений скорости и ускорения привода, и с угловой скоростью Vc в момент совпадения углов Вр и Вс. Т.е. необходимо найти зависимость: АЛГОРИТМ Для достижения минимального времени преодоления приводом текущего рассогласования в текущем такте n, равного dBn=Bc-Bt, привод должен двигаться со скоростью Vp, позволяющей остановку двигателя в точке Вс, при торможении с максимальным ускорением Wmax, т.е. скорость привода в точке текущего такта должна определяться: Vp(dTmin)=Vpn+Wmax Последнее выражение имеет смысл при разных знаках величин Vp+Wmax. За время dTmin привод должен обеспечить приращение угла dBn: dBn=Vpn Учитывая (16), получим: dBn=Vpn Скорость в точке Bn для остановки привода в заданной точке при торможении с максимальным ускорением должна быть: Последнее выражение имеет смысл при разных знаках величин dBn и Wmax, а учитывая, что Vp и Wmax также должны иметь разные знаки, знак Vpn должен совпадать со знаком dBn: Следовательно, для обработки рассогласования dBn за минимальное время и остановки привода в точке Вс привод должен отслеживать на каждом шаге n некоторую расчетную скорость Vp, т.е. привод должен разгоняться, если его фактическая скорость меньше расчетной Vp, и тормозиться, если его фактическая скорость выше расчетной. Последнее возможно при торможении с ускорением большим, чем Wmax, что противоречит принятым условиям задачи. Поэтому оптимальная скорость привода в точке Bn должна рассчитываться на торможение с ускорением меньшим, чем Wmax: Wp=Kw Kw – коэффициент «запаса» привода по ускорению. При этом время перемещения привода в заданную точку будет не минимальным, а близким к нему, но чем ближе Kw к единице, тем хуже управляемость привода. Скорость привода в точке текущего такта с учетом изложенного должна быть: Сигнал управления приводом СО: Vt – фактическое текущее значение скорости привода. На первый взгляд, управление приводом по (20) осуществляется только по разности скоростей и не зависит от углового рассогласования. Но, в соответствии с (19), расчетная скорость привода полностью зависит от величины рассогласования по углу, т.е. управление осуществляется и по угловому рассогласованию с учетом разности заданной и фактической скорости привода. Рассмотрим случай неподвижной точки цели. Текущее рассогласование между азимутами цели и привода на текущем шаге измерения: dBt=Bc-Вр Минимальное время для остановки привода на азимуте цели возможно при максимально допустимом ускорении привода Wp: |dBt|=(Wp dT=sqrt(2 Vt=sqrt(2 Vt=Vmax, если Vt>Vmax При этом скорость привода: Vt=Wp Модуль приращения углового положения привода за промежуток квантования dT | При достаточно малом dT вторым членом последнего равенства можно пренебречь. | Знак (sign) приращения |
Величина COn=sign(dBn) Это позволит при малой крутизне характеристики регулирования в зоне малых ошибок регулирования уменьшить «рывки» привода при малых рассогласованиях и увеличить чувствительность привода при увеличении рассогласования. При перемещении точки цели со скоростью Vc необходимо в текущей точке Bn обеспечить такую скорость привода Vp, которая при торможении с заданным ускорением Wp обеспечит при малом dBn скорость привода, равную скорости цели: Wp При этом привод должен обеспечить перемещение по В dBp=dBn+Vp Используя dT из (21) и dBp из (22), получаем: Vp-Vc=(+-)sqrt(2 Знаки dBn и (Вр-VBc) должны совпадать: Vp=sign(dBn) Рассогласование: ПАРАМЕТРЫ ПРИВОДА Привод однозначно определяется параметрами: ТЭ – электрическая постоянная времени, ТЭМ – электромеханическая постоянная времени, Кр – коэффициент усиления. Для вычисления управляющих воздействий используются ТЭМ и Кр. Способы измерения этих параметров приведены ниже. Зададим постоянное управляющее воздействие SП на интервале времени от нуля до t1. Движение привода описывается следующими выражениями: скорость на интервале от нуля до t1: пройденный путь за время t1: скорость в точке t1: скорость на интервале от t1 до остановки привода: пройденный путь за время от t1 до остановки: полный путь за время от нуля до остановки: Значение Кр можно получить из выражения для полного пути до остановки. Для определения Кр нужно: – задать рассогласование SП длительностью tn; – измерить перемещение привода Bэ; – вычислить: Значение ТЭМ можно определить из выражения для скорости V1, измеренной в момент t1: Если величина ТЭ составляет менее одной сотой от величины Тэм, точность определения ТЭМ по скорости V1 достаточна. В противном случае Тэм определяется: TЭМ=(SП·tn-B1m)/V1m, где V1m – скорость в точке t1m, когда V достигнет максимума, B1m – путь, пройденный от 0 до точки t1m. РЕАЛИЗАЦИЯ АЛГОРИТМА Текущее значение входного сигнала определяется по разнице скоростей между текущей скоростью привода и текущей расчетной скоростью: CO=Vp-Vt Расчетная скорость: Vp=sign(dBp) где Vc – текущая скорость точки цели; Wc – ускорение точки цели; dT – длительность такта выдачи управляющих воздействий на привод; Wp – ускорение привода; sign(dBp) – единица, если dBp больше или равно нулю, иначе – минус единица. Расчетное ускорение привода: Wp=Kw где Kw – коэффициент «запаса» по ускорению; Wmax – максимальное ускорение привода. Максимальное ускорение привода: Wmax=Vmax/Тэм, где Vmax – максимальная скорость привода; Тэм – электромеханическая постоянная времени. Максимальная скорость привода: Vmax=К Am, где К – коэффициент усиления; Am – максимальное значение входного сигнала на привод. dBp – текущее рассогласование по координате привода и точке цели. Расчетное рассогласование по координате: dBp=(Bc-Bt)+(Vc-Vt) где Bc – текущая координата точки цели; Bt – текущая координата привода; Vc – текущая скорость точки цели; Vt – текущая скорость привода. Если полученное значение СО по модулю превышает значение заданного максимального входного сигнала Am, принимается значение СО, по модулю равное Am. Промышленная применимость Данный способ промышленно реализуем, обладает хорошими динамическими характеристиками, высокой скоростью подвода луча локатора к точке цели и точностью ее сопровождения. Подобный алгоритм использован на ФГУП «НПП «Рубин» для решения задачи автоматизации управления приводом ССЦ в боевой машине «Оса». При разработке и исследовании данной методики была создана программная модель привода, на которой были проверены основные решения. Натурные проверки на образце выявили высокую актуальность решаемой задачи и преимущества разработанной модели. Предлагаемый способ (алгоритм) реализован в программе для ЭВМ «Программа решения задачи Встречи (KEXTRAN) (РДПИ.00551-01)», Свидетельство о регистрации №2000611122 от 04.09.2000, правообладатель ФГУП «НПП «Рубин», авторы: Пархоменко О.Л., Новосельцев О.Ф., Кошелев А.В., Падусенко Л.А.
Формула изобретения
Способ автоматического регулирования положения привода с помощью аппаратуры приема и реализации целеуказания, содержащей электронную вычислительную машину и блоки ввода и вывода дискретной информации по трем координатам в полярной системе координат управления приводом, отличающийся тем, что в данном способе сигнал ошибки определяют по разности скорости привода и скорости фиктивной расчетной точки, для вычисления которой используются параметры системы регулирования, а также положение, скорость и ускорение объекта и точки наведения, управление объектом осуществляют по трем координатам в полярной системе координат и выполняют следующие шаги алгоритма (управление по каждой координате выполняется одинаково): шаг 1 – ввод текущих координат точки цели (Хс Yc Hc) от станции обнаружения, предназначенных для наведения радиолокационной станции (РЛС) станции сопровождения в окрестность текущей точки цели; шаг 2 – вычисление усредненных значений координат и составляющих скоростей по текущим координатам точки цели методом «скользящее окно»: Xcs=Xcs+Vxs·dT, dX=Xc-Xcs, dVx=dX/dT, Xcs=Xcs+Kk·dX, Vxs=Vxs+Kv·dVx, где Xcs – усредненная координата; Vxs – усредненная скорость; Kk – коэффициент усреднения для координаты; Kv – коэффициент усреднения для скорости; dT – интервал времени между последними поступлениями координат от станции обнаружения; шаг 3 – экстраполирование усредненных координат точки цели на текущий момент времени Xct=Xcs+Vxs·DT, где Xct – текущая координата; DT – длительность такта выдачи сигналов рассогласований на привода РЛС станции сопровождения; шаг 4 – перевод экстраполированных координат точки цели в полярную систему координат и вычисление составляющих скорости точки цели в полярной системе координат Dg=sqrt(Xct·Xct+Yct·Yct), DC=sqrt(Dg+Hct·Hct), Bc=atan(Yct/Xct), EC=asin(Hct/Dc), VBc=(XctVys-YctVxs)/(Dg·Dg), VEc=[Dg·Vhs-Hct·(XctVxs-Yet·Vys)/Dg]/(Dc·Dc), VDc=(Xct·Vxs+Yct·Vys+Hct·Vhs)/Dc, где Dg, Dc – горизонтальная и наклонная дальность; Bc, Ec – азимут и угол места; VBc, VEc, VDc – составляющие скорости по азимуту, углу места и дальности; шаг 5 – изменение и ввод в компьютер (от датчиков) текущих фактических координат положения приводов (Вр Ер Dp); шаг 6 – вычисление текущих фактических скоростей приводов VBp=(Bp-Bp1)/DT1, VEp=(Ep-Ep1)/DT1, VDp=(Dp-Dp1)/DT1, где Bp, Ep, Dp – текущие координаты положения приводов; Bp1, Ep1, Dp1 – значения координат приводов, измеренные на время DT1 ранее текущего времени; DT1 – временной интервал измерения скорости приводов; шаг 7 – вычисление расчетной скорости привода РЛС станции сопровождения по угловому рассогласованию между фактическим положением точки цели и фактическим положением привода при условии максимального значения ускорения привода и с учетом фактической скорости точки цели VBP=sign(dBP)·sqrt(2·abs(dBP)·WBP)+VBc+WBc·DT, где VBc – текущая скорость точки цели; WBc – изменение скорости точки цели на интервале dT WBc=(VBc-VBcl)/dT, где VBcl – скорость точки цели во время на dT ранее текущего времени; WBP – расчетное ускорение привода по азимуту WBP=KWP·WBmax, где KWP – коэффициент «запаса» по ускорению; WBmax – максимальное ускорение привода по азимуту WBmax=VBmax/ТВэм, где ТВэм – электромеханическая постоянная времени привода по азимуту; VBmax – максимальная скорость привода по азимуту VBmax=KB·ABm, где KB – коэффициент усиления привода азимута; ABm – максимальное значение входного сигнала на привод азимута; dBP – рассогласование по азимуту точки цели и привода РЛС станции сопровождения; dBP=(Вс-Вр)+(VBc-VBp)·dT, sign(dBP) – знак рассогласования по азимуту точки цели и привода; abs(dBP) – абсолютное значение рассогласования по азимуту точки цели и привода РЛС станции сопровождения; шаг 8 – вычисление сигналов ошибки по разнице расчетной скорости привода, которая должна быть в текущий момент времени для уменьшения угловых рассогласований между положением точки цели и привода при максимальном значении ускорения привода, и фактической скоростью привода SOB-VBP-VBp, SOE=VEP-VEp, SOD=VBD-VDp, если полученное значение SOB по модулю превышает значение максимального входного сигнала ABm, принимается значение SOB, по модулю равное ABm; шаг 9 – выдача сигналов ошибки SOB, SOE, SOD на входные регистры привода азимута, привода угла места и привода дальности РЛС станции сопровождения.
|
||||||||||||||||||||||||||

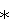 dT,
dT, Vmax
Vmax


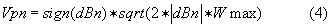


 В|n+1=Vn
В|n+1=Vn