Патент на изобретение №2268080

(54) СИММЕТРИЧНЫЙ 32-ГРАННИК

(57) Реферат:

Симметричный 32-гранник относится к игровым элементам и может быть использован в качестве игральной кости. Симметричный 32-гранник содержит тридцать две грани, двадцать из которых являются шестиугольниками, а двенадцать – правильными пятиугольниками. Площади всех граней одинаковы, а их центры тяжести симметричны относительно центра симметрии 32-гранника. Шестиугольные грани образованы сторонами, имеющими два разных размера и расположенными напротив друг друга. Симметричный 32-гранник обеспечивает равную вероятность выпадения каждой грани. 3 ил.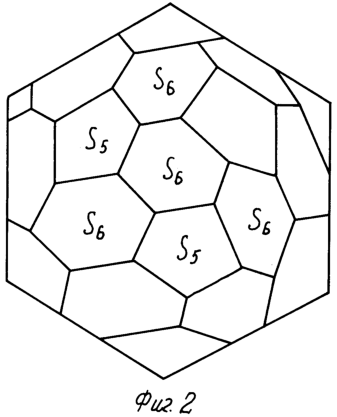

Изобретение предназначено для использования в качестве игрового элемента в различных вероятностных играх, лотереях и др.

Известно много игровых элементов, позволяющих формировать случайные события в виде выпадения определенного знака или цифры, размещенных на их сторонах и гранях. Особенно распространены элементы, выполненные в виде правильных многогранников, при этом важное значение имеет количество случайных событий, исходов, умещающихся на элементе. Например, монета имеет два исхода, кубик – шесть, додекаэдр – 12, а икосаэдр – чемпион среди правильных многогранников – 20. К сожалению, это – предел. С большим числом граней математически правильных многогранников нет и быть не может. А очень хотелось бы иметь, скажем, правильный 1000000-гранник. Бросил один раз и можно выиграть миллион за поставленный рубль. Не часто, понятно, но можно. Однако таких игровых элементов нет и приходится прибегать к всевозможным шаровым и прочим лототронам, где сместить в свою пользу счастье значительно проще, чем у многогранника. Таким образом, увеличение объема информации, несущей игровым элементом, т.е. числа его граней, полезно, ибо уменьшает возможность обманов.

Одним из наиболее близких аналогов является симметричный 32-гранник для использования в качестве игрового элемента, содержащий тридцать две грани, двадцать из которых являются шестиугольниками, а двенадцать – правильными пятиугольниками (JP 2003 – 190621 А (MARK-I INC.), 08.07.2003).

Задачей заявленного изобретения является расширение арсенала технических средств – многогранников для использования в качестве игрового элемента (игральной кости). Технический результат заключается в реализации вышеуказанного назначения.

Технический результат достигается тем, что в симметричном 32-граннике для использования в качестве игрового элемента, содержащем тридцать две грани, двадцать из которых являются шестиугольниками, а двенадцать – правильными пятиугольниками, площади всех граней одинаковы, а их центры тяжести симметричны относительно центра симметрии 32-гранника, при этом шестиугольные грани образованы сторонами, имеющими два разных размера и расположенными напротив друг друга.

Теоретически правильный многогранник должен иметь все грани из правильных многоугольников и в каждой вершине должно сходиться одно и то же число этих граней. Однако эта норма превышает игровое требование, заключающееся в одинаковой вероятности выпадения любой грани. Для этого необходимо, чтобы все грани имели одинаковую площадь и их центры тяжести были расположены симметрично относительно друг друга и центра симметрии многогранника.

Изобретение поясняется чертежами.

На фиг.1 изображен классический икосаэдр;

на фиг.2 изображен заявляемый 32-гранник (усеченный икосаэдр);

на фиг.3 изображен процесс трансформации икосаэдра в триакостодефтероэдр (усеченный икосаэдр).

Изобретение описывает симметричный многогранник с числом граней Г=32 – усеченный икосаэдр (триакостодефтероэдр, греч.). Симметричный 32-гранник для использования в качестве игрового элемента содержит тридцать две грани. Двадцать граней являются шестиугольниками, а двенадцать – правильными пятиугольниками. Площади всех граней одинаковы, а их центры тяжести симметричны относительно центра симметрии 32-гранника. Шестиугольные грани образованы сторонами, имеющими два разных размера и расположенными напротив друг друга.

Для изготовления предлагаемого 32-гранника у икосаэдра (фиг.1) спиливают все вершины пирамид таким образом, чтобы площади оставшихся пятиугольников S₅ были равны площадям, возникших при этом шестиугольников S₆ – остатков граней исходного икосаэдра (фиг.3). Это будет достигнуто, если расстояния оа=ов=0,378с, где с – длина ребра исходного икосаэдра (фиг.3). Значение “с” находится из уравнения

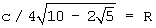, где R – радиус описанной сферы исходного икосаэдра.

Таким образом, поверхность полученного 32-гранника состоит из 12 равносторонних пятиугольников (оснований срезанных вершин) и 20 шестиугольников (остатков треугольных граней исходного икосаэдра), стороны которых равны 0.378с и 0,244с, площади их равны площадям упомянутых пятиугольных граней, а центры тяжести всех граней симметричны относительно центра симметрии триакостодефтероэдра (усеченного икосаэдра – 32-гранника). Эти обстоятельства обеспечивают равную вероятность выпадения каждой грани, что подтверждается экспериментально. Поэтому такой симметричный многогранник в вероятностных играх эквивалентен каноническим “телам Платона”, но превышает их по содержательности.

Формула изобретения

Симметричный тридцатидвухгранник для использования в качестве игрового элемента, содержащий тридцать две грани, двадцать из которых являются шестиугольниками, а двенадцать – правильными пятиугольниками, отличающийся тем, что площади всех граней одинаковы, а их центры тяжести симметричны относительно центра симметрии тридцатидвухгранника, при этом шестиугольные грани образованы сторонами, имеющими два разных размера и расположенными напротив друг друга.

РИСУНКИ