|
|
(21), (22) Заявка: 2003115683/09, 26.05.2003
(24) Дата начала отсчета срока действия патента:
26.05.2003
(43) Дата публикации заявки: 27.11.2004
(45) Опубликовано: 10.08.2005
(56) Список документов, цитированных в отчете о
поиске:
SU 809154 A1, 28.02.1981. SU 601688 A, 05.04.1978. SU 1226670 A, 23.04.1986. ЕР 0357212 А2, 07.03.1990. ЕР 0482376 А2, 29.04.1992. US 4825401 А, 25.04.1989. КОМАШАНСКИЙ В.И. и др. Нейронные сети и их применение в системах управления и связи. М.: Горячая линия Телеком, 2002, с.8, с.14, рис.1.5.
Адрес для переписки:
355017, г.Ставрополь, ул. Артема, 2, ФРВИ РВ, НИО
|
(72) Автор(ы):
Червяков Н.И. (RU),
Сивоплясов Д.В. (RU)
(73) Патентообладатель(и):
Червяков Николай Иванович (RU),
Сивоплясов Дмитрий Владимирович (RU)
|
(54) НЕЙРОННАЯ СЕТЬ ДЛЯ ПРЕОБРАЗОВАНИЯ ПОЛИАДИЧЕСКОГО КОДА В КОД СИСТЕМЫ ОСТАТОЧНЫХ КЛАССОВ
(57) Реферат:
Изобретение относится к вычислительной технике и может быть использована в модулярных нейрокомпьютерах для быстрого восстановления остаточных чисел, закодированных в полиадической системе счисления (ОПСС). Техническим результатом является повышение быстродействия перевода чисел из ОПСС в систему остаточных классов (СОК), а также сокращение оборудования. Для этого нейронная сеть содержит входной слой и нейронные сети конечного кольца. 1 ил. 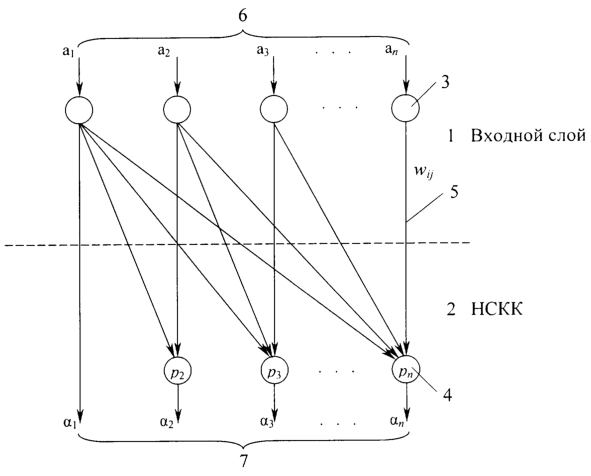
Изобретение относится к вычислительной технике и может быть использовано в модулярных нейрокомпьютерах для быстрого восстановления остаточных чисел, закодированных в полиадической системе счисления, иногда называемой обобщенной позиционной системой счисления (ОПСС).
Известен преобразователь позиционного кода в вычет по модулю (АС СССР №1383506 Н 03 Н 7/18, 1988 г.), содержащий регистр сдвига, группу элементов И, регистр, блок умножения по модулю, накапливающий сумматор по модулю. Недостатком известного преобразователя являются сложность устройства и низкое быстродействие.
Наиболее близким по технической сущности к предлагаемому является преобразователь полиадического кода в код системы остаточных классов (СОК) (АС СССР №809154, МКЛ3 G 06 F 5/02, 1981 г.), содержащий входной регистр, дешифраторы, ключи, матричные сумматоры.
Однако известный преобразователь имеет низкое быстродействие и требует больших аппаратурных затрат.
Цель изобретения – повышение быстродействия перевода чисел представленных в ОПСС, в СОК и сокращение оборудования.
Указанная цель достигается тем, что преобразователь содержит входной слой нейронов и нейронную сеть прямого распространения, состоящей из n-нейронных сетей конечного кольца по модулю р, системы остаточных классов (где n – количество модулей системы, i=1, 2,…, n).
Исходными данными для нейронной сети является полиадический код An=[a1,a2,…,an], а выходными данными является остаточный код A0=( 1, 1, 2,…, 2,…, n), таким образом нейронная сеть решает задачу соответствия n), таким образом нейронная сеть решает задачу соответствия
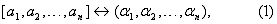
Пусть число Аn представлено в ОПСС в виде выражения
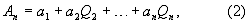
где 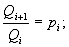 Q1=1; (i=1, 2,…, n). Q1=1; (i=1, 2,…, n).
Тогда
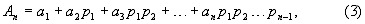
где pi – основания полиадической системы счисления;
аi – коэффициенты ОПСС.
Если взять одни и те же pi в качестве оснований СОК и ОПСС, тогда диапазоны чисел, представленных в СОК и ОПСС будут одинаковыми, следовательно, выполняется соответствие (1).
Пусть р1,р2,…,рn – попарно взаимно простые целые числа
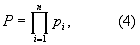
и
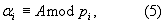
Тогда соответствия А ( ( 1, 1, 2,…, 2,…, n) между целыми числами в интервале [0,l) и набором вида ( n) между целыми числами в интервале [0,l) и набором вида ( 1, 1, 2,…,а3), 0< 2,…,а3), 0< i i
i, 0 i1, i1, 2,…, 2,…, n) называется модулярным представлением числа А. n) называется модулярным представлением числа А.
Пусть известно представление числа Аn в ОПСС (3), найти его представление в СОК.
Так как основания pi в СОК и ОПСС постоянны, то значения Q1,Q2, Qn можно представить в виде разрядов СОК, которые являются константами при выбранных модулях системы:
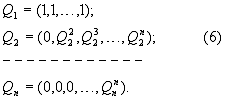
Тогда из выражений (2, 3) следует, что цифры СОК ( 1, 1, 2,…, 2,…, n) можно найти из сравнений: n) можно найти из сравнений:

Если в системе (7) числа a1, a2,…, аn являются известными, так как число представлено в ОПСС (2, 3), то решение этой системы сравнений дает значения ( 1, 1, 2,…, 2,…, n), которые являются разрядами числа, представленного в СОК. n), которые являются разрядами числа, представленного в СОК.
Для иллюстрации вышеуказанного приведем численный пример.
Переведем число Аn=[1,1,0,0], представленное в ОПСС, в СОК по основаниям p1=2, p2=3, p3=5, p4=1.
Представим константы Q1 Q2, Q3, Q4 в СОК, тогда:
Q1=1=(1,1,1,1);
Q2=2=(0,2,2,2);
Q3=6=(0,0,1,6);
Q4=30=(0,0,0,2).
Тогда на основании выражения (7) запишем
А0=(1,1+1·2,1+1·2+0,1+1·2+0·6+0·2)=(1,0,3,3).
Таким образом, число Аn=[1,1,0,0], представленное в ОПСС выглядит как число А0=(1,0,3,3), представленное в СОК по основаниям р1=2, р2=3, р3=5,р4=7.
На чертеже представлена структура нейронной сети для преобразования полиадического кода в код системы остаточных классов.
Нейронная сеть состоит из входного слоя, связанного с нейронной сетью конечного кольца. Структура нейронной сети может адаптироваться к определенным внешним параметрам. Преобразование кода нейронной сетью определяется модулями системы остаточных классов и весовыми коэффициентами между нейронами входного слоя и нейронами скрытого слоя нейронной сети конечного кольца (НСКК). В зависимости от величины модуля и от весовых коэффициентов изменяется код системы остаточных классов.
При выбранных модулях СОК структура нейронной сети зависит от одного внешнего параметра и адаптируется к нему посредством загрузки весовых коэффициентов. Посредством весовых коэффициентов нейронная сеть осуществляет преобразование кода на основе четко сформулированного в нейросетевом базисе алгоритма преобразования. Такие сети относятся к формируемым сетям и не требуют предварительного обучения.
Функционирование нейронной сети зависит от весовых коэффициентов между слоями нейронов, которые определяются на этапе проектирования сети.
Процесс преобразования происходит активизацией определенных выходов нейронной сети конечного кольца, значения преобразуемых кодов определяются весовыми коэффициентами. НСКК выполняет операцию по модулю pi. В этой сети функция активации не используется и нейрон выполняет оператор по модулю pi.
Нейронная сеть (см. чертеж) содержит входной слой 1 с нейронами 3, НСКК 2 с нейронами 4, весовые коэффициенты 5, входной полиадический код 6 и выходной код СОК 7. Нейронная сеть преобразует входной код 6, представленный в ОПСС в код СОК 7. Входной код поступает на вход нейронов 3, расположенных во входном слое 1, преобразованный код СОК появляется в выходном слое НСКК 2 в нейронах 4. Между входным слоем 1 и НСКК 2 расположены связи между нейронами, обозначены 5. Значения весовых коэффициентов wij определяется выражением (6) wij=Qj i,(i,j=1,2,…,n). Нейронная сеть конечного кольца реализует вычислительную модель (7). Определенные внешние параметры заданы в весовых коэффициентах wij и хранятся в памяти. Из памяти по требованию могут загружаться новые весовые коэффициенты для новых модулей СОК и ОПСС, определяя при этом структуру нейронной сети (чертеж), в которой достигается самое быстрое и надежное преобразование кода. Время преобразования кода определяется одним тактом синхронизации, что и отличает предлагаемое изобретение от известных, у которых время преобразования определяется n-циклами синхронизации, где n – число оснований ОПСС и СОК.
Формула изобретения
Нейронная сеть для преобразования полиадического кода в код системы остаточных классов содержит входной слой нейронов, предназначенный для приема полиадического кода аi, и нейронные сети конечного кольца, при этом выходы нейронов входного слоя разветвлены на входы нейронных сетей конечного кольца, выходы которых являются выходами упомянутой нейронной сети для преобразования полиадического кода в код системы остаточных классов, отличающаяся тем, что нейронные сети конечного кольца предназначены для вычисления

где  n – числа кода системы остаточных классов, pi – основания системы счисления, n – числа кода системы остаточных классов, pi – основания системы счисления, 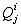 – константы при выбранных основаниях системы и формирования выходного кода системы остаточных классов. – константы при выбранных основаниях системы и формирования выходного кода системы остаточных классов.
РИСУНКИ
MM4A – Досрочное прекращение действия патента СССР или патента Российской Федерации на изобретение из-за неуплаты в установленный срок пошлины за поддержание патента в силе
Дата прекращения действия патента: 27.05.2006
Извещение опубликовано: 10.06.2007 БИ: 16/2007
|
|