|
|
(21), (22) Заявка: 2003110409/09, 13.08.2002
(24) Дата начала отсчета срока действия патента:
13.08.2002
(30) Конвенционный приоритет:
14.08.2001 (пп.1-4) KR 2001-48921
(43) Дата публикации заявки: 20.09.2004
(45) Опубликовано: 27.05.2005
(56) Список документов, цитированных в отчете о
поиске:
JP 08214035 A, 20.08.1996. RU 2019050 C1, 30.08.1994. JP 11068876 А, 09.03.1999. ЕР 0957614, 17.11.1999. ЕР 0841756 А, 13.05.1998.
(85) Дата перевода заявки PCT на национальную фазу:
11.04.2003
(86) Заявка PCT:
KR 02/01546 (13.08.2002)
(87) Публикация PCT:
WO 03/017609 (27.02.2003)
Адрес для переписки:
129010, Москва, ул. Б. Спасская, 25, стр.3, ООО “Юридическая фирма Городисский и Партнеры”, пат.пов. Ю.Д.Кузнецову, рег.№ 595
|
(72) Автор(ы):
ХА Санг-Хиук (KR),
КИМ Мин-Гоо (KR)
(73) Патентообладатель(и):
САМСУНГ ЭЛЕКТРОНИКС КО., ЛТД. (KR)
|
(54) УСТРОЙСТВО И СПОСОБ ДЕМОДУЛЯЦИИ В СИСТЕМЕ СВЯЗИ, ИСПОЛЬЗУЮЩЕЙ МОДУЛЯЦИЮ 8-РИЧНОЙ ФАЗОВОЙ МАНИПУЛЯЦИЕЙ
(57) Реферат:
Изобретение относится к радиотехнике. Технический результат заключается в отсутствии сложной обработки, требуемой для получения значения минимального расстояния для принимаемого сигнала. Сущность изобретения заключается в том, что устройство демодуляции сигналов 8-ричной ФМ принимает входной сигнал Rk(Xk,Yk), содержащий k-ую квадратурную составляющую Yk и k-ую синфазную составляющую Xk, и для генерирования значений L(sk,0), L(sk,1) и L(sk,2) мягкого решения. Вычислитель вычисляет Zk путем вычитания уровня |Yk| квадратурной сигнальной составляющей Yk из уровня |Xk| синфазной сигнальной составляющей Xk. Первый селектор выбирает Zk соответственно наиболее значимому биту (MSB) квадратурной сигнальной составляющей Yk. Второй селектор выбирает Zk соответственно MSB синфазной сигнальной составляющей Xk. Третий селектор выбирает выходной сигнал второго селектора или значение “0” соответственно MSB в Zk. 4 н.п. ф-лы, 5 ил., 7 табл.
Область техники
Настоящее изобретение относится к устройству и способу демодуляции в цифровой системе связи, использующей многоуровневую модуляцию, в частности к устройству и способу демодуляции, для вычисления значений мягкого решения, необходимых в качестве входных сигналов для канального декодера в демодуляторе для цифровой системы связи, использующей модуляцию 8-ричной фазовой манипуляцией (ФМ).
Предшествующий уровень техники
В цифровой системе связи, использующей модуляцию 8-ричной ФМ, представляющую собой вид многоуровневых модуляций, используемых для повышения спектральной эффективности, сигнал, кодированный канальным кодером, передается после осуществления его модуляции. Затем демодулятор демодулирует переданный сигнал и выдает демодулированный сигнал на канальный декодер для декодирования. Канальный декодер выполняет декодирование мягкого решения для коррекции ошибок. Для выполнения этого демодулятор должен иметь алгоритм отображения для генерирования значений мягкого решения (или мягких значений), соответствующих выходным битам канального кодера, из двумерного сигнала, состоящего из синфазной сигнальной составляющей и квадратурной сигнальной составляющей.
Алгоритмы отображения классифицируются на процедуру простой метрики, предложенную компанией Nokia, и процедуру метрики двойного минимума, предложенную компанией Motorola. Оба алгоритма вычисляют логарифмическое отношение правдоподобия (LLP) для выходных битов и используют вычисленные LLP в качестве входного значения мягкого решения для канального декодера.
Процедура простой метрики, представляющая собой алгоритм отображения, задаваемый путем модифицирования формулы комплексного вычисления LLP, в простую приближенную формулу, имеет простую формулу вычисления LLP, но искажение LLP, вызванное использованием приближенной формулы, приводит к ухудшению рабочих характеристик. Процедура метрики двойного минимума, представляющая собой алгоритм отображения для вычисления LLP с использованием более точной приближенной формулы и использующая вычисленное LLP в качестве входного и значения мягкого решения канального декодера, может до некоторой степени восполнить ухудшение рабочих характеристик процедуры простой метрики. Однако по сравнению с процедурой простой метрики данная процедура требует большего объема вычислений, что приводит к значительному увеличению сложности аппаратных средств.
Сущность изобретения
Поэтому задачей настоящего изобретения является создание устройства и способа для упрощения получения входных значений мягкого решения канального декодера, вычисленных по процедуре метрики двойного минимума, без использования таблицы отображения или сложной обработки, требуемой для получения значения минимального расстояния для принимаемого сигнала, в демодуляторе для цифровой системы связи, использующей модуляцию 8-ричной ФМ.
Также задачей настоящего изобретения является создание устройства и способа для вычисления значений мягкого решения по простой условной формуле в цифровой системе связи, использующей модуляцию 8-ричной ФМ.
Для достижения указанных и других результатов, предложено устройство демодуляции 8-ричной ФМ для приема входного сигнала Rk(Xk,Yk), содержащего k-ю квадратурную составляющую Yk и k-ю синфазную составляющую Xk, и для генерирования значений  (sk,0), (sk,0),  (sk,1) и (sk,1) и  (sk,2) мягкого решения для входного сигнала Rk(Xk,Yk) с помощью средства мягкого решения. Устройство содержит вычислитель для вычисления мягкого значения Zk путем вычитания уровня |Yk| квадратурной сигнальной составляющей Yk из уровня |Xk| синфазной сигнальной составляющей Xk принятого сигнала Rk(Xk,Yk) и выдачи Zk в качестве первого значения мягкого решения; первый селектор для приема Zk от вычислителя и инвертированного значения -Zk для Zk и выбора Zk или -Zk соответственно наиболее значимому биту (MSB) квадратурной сигнальной составляющей Yk; второй селектор для приема Zk от вычислителя и -Zk и выбора Zk или -Zk соответственно MSB синфазной сигнальной составляющей Xk; третий селектор для приема выходного сигнала второго селектора и значения “0” и выбора выходного сигнала второго селектора или значения “0” соответственно MSB функции Zk; первый сумматор для суммирования значения, вычисленного путем умножения квадратурной сигнальной составляющей Yk на (sk,2) мягкого решения для входного сигнала Rk(Xk,Yk) с помощью средства мягкого решения. Устройство содержит вычислитель для вычисления мягкого значения Zk путем вычитания уровня |Yk| квадратурной сигнальной составляющей Yk из уровня |Xk| синфазной сигнальной составляющей Xk принятого сигнала Rk(Xk,Yk) и выдачи Zk в качестве первого значения мягкого решения; первый селектор для приема Zk от вычислителя и инвертированного значения -Zk для Zk и выбора Zk или -Zk соответственно наиболее значимому биту (MSB) квадратурной сигнальной составляющей Yk; второй селектор для приема Zk от вычислителя и -Zk и выбора Zk или -Zk соответственно MSB синфазной сигнальной составляющей Xk; третий селектор для приема выходного сигнала второго селектора и значения “0” и выбора выходного сигнала второго селектора или значения “0” соответственно MSB функции Zk; первый сумматор для суммирования значения, вычисленного путем умножения квадратурной сигнальной составляющей Yk на 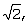 с выходным значением третьего селектора, и выдачи результирующего значения в качестве третьего значения мягкого решения; четвертый селектор для приема выходного сигнала второго селектора и значения “0” и выбора выходного сигнала второго селектора или значения “0” соответственно MSB функции Zk; и второй сумматор для суммирования значения, вычисленного путем умножения синфазной сигнальной составляющей Xk на с выходным значением третьего селектора, и выдачи результирующего значения в качестве третьего значения мягкого решения; четвертый селектор для приема выходного сигнала второго селектора и значения “0” и выбора выходного сигнала второго селектора или значения “0” соответственно MSB функции Zk; и второй сумматор для суммирования значения, вычисленного путем умножения синфазной сигнальной составляющей Xk на 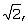 с выходным значением четвертого селектора, и выдачи результирующего значения в качестве второго значения мягкого решения. с выходным значением четвертого селектора, и выдачи результирующего значения в качестве второго значения мягкого решения.
Для достижения указанных и других результатов предложен способ демодуляции 8-ричной ФМ для приема входного сигнала Rk(Xk,Yk), содержащего k-ю квадратурную составляющую Yk и k-ю синфазную составляющую Хk, и для генерирования значений  (sk,0), (sk,0),  (sk,1) и (sk,1) и  (sk,2) мягкого решения для входного сигнала Rk(Xk,Yk) с помощью средства мягкого решения. Способ включает этапы: а) вычисления мягкого значения Zk первого демодулированного символа путем вычитания уровня |Yk| квадратурной сигнальной составляющей Yk из уровня |Хk| синфазной сигнальной составляющей Xk принятого сигнала Rk(Xk,Yk), b) установки первой переменной (sk,2) мягкого решения для входного сигнала Rk(Xk,Yk) с помощью средства мягкого решения. Способ включает этапы: а) вычисления мягкого значения Zk первого демодулированного символа путем вычитания уровня |Yk| квадратурной сигнальной составляющей Yk из уровня |Хk| синфазной сигнальной составляющей Xk принятого сигнала Rk(Xk,Yk), b) установки первой переменной  на “0”, если мягкое значение Zk имеет положительное значение, установки первой переменной на “0”, если мягкое значение Zk имеет положительное значение, установки первой переменной  на “-1”, если мягкое значение Zk имеет отрицательное значение и квадратурная составляющая Yk имеет положительное значение, и установки первой переменной на “-1”, если мягкое значение Zk имеет отрицательное значение и квадратурная составляющая Yk имеет положительное значение, и установки первой переменной  на “1”, если Zk имеет отрицательное значение и квадратурная составляющая Yk имеет отрицательное значение, с) определения мягкого значения третьего демодулированного символа путем вычисления на “1”, если Zk имеет отрицательное значение и квадратурная составляющая Yk имеет отрицательное значение, с) определения мягкого значения третьего демодулированного символа путем вычисления 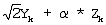 с использованием квадратурной составляющей Yk, мягкого значения Zk и первой переменной с использованием квадратурной составляющей Yk, мягкого значения Zk и первой переменной  ; d) установки второй переменной ; d) установки второй переменной  на “0”, если мягкое решение Zk имеет отрицательное значение, установки второй переменной на “0”, если мягкое решение Zk имеет отрицательное значение, установки второй переменной  на “-1”, если Zk имеет положительное значение и синфазная составляющая Xk имеет отрицательное значение, и установки второй переменной на “-1”, если Zk имеет положительное значение и синфазная составляющая Xk имеет отрицательное значение, и установки второй переменной  на “1”, если Zk имеет положительное значение и синфазная составляющая Xk имеет положительное значение; е) определения мягкого значения второго демодулированного символа путем вычисления на “1”, если Zk имеет положительное значение и синфазная составляющая Xk имеет положительное значение; е) определения мягкого значения второго демодулированного символа путем вычисления 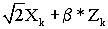 с использованием синфазной составляющей Xk, мягкого значения Zk и второй переменной с использованием синфазной составляющей Xk, мягкого значения Zk и второй переменной  . .
Краткое описание чертежей
Вышеуказанные и другие задачи, признаки и преимущества настоящего изобретения поясняются в последующем детальном описании со ссылками на чертежи, на которых представлено следующее:
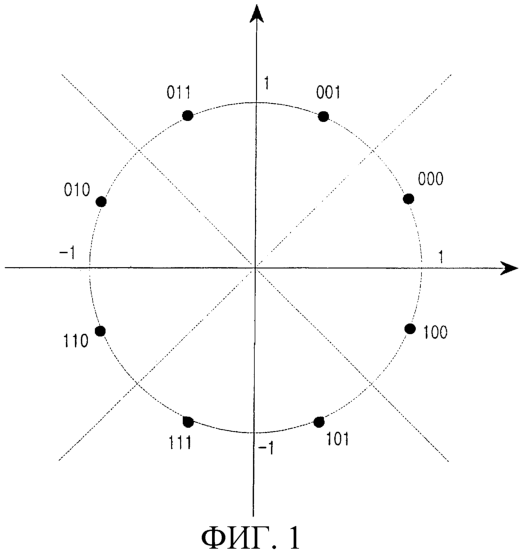
Фиг.1 – совокупность сигналов с точками отображения согласно 8-ричной ФМ;
Фиг.2 – процедура вычисления значений мягкого решения в цифровой системе связи, использующей 8-ричную ФМ в соответствии с возможным вариантом осуществления настоящего изобретения;
Фиг.3 – блок-схема вычислителя для определения значений мягкого решения для демодулированных символов в соответствии с возможным вариантом осуществления настоящего изобретения;
Фиг.4 – логическая схема вычислителя значения мягкого решения для применения в цифровой системе связи, использующей 8-ричную ФМ, и
Фиг.5 – совокупность сигналов с точками отображения согласно 8-ричной ФМ, для пояснения вычислений.
Детальное описание предпочтительного варианта осуществления изобретения
Предпочтительный вариант осуществления настоящего изобретения описан ниже со ссылками на иллюстрирующие чертежи. В последующем описании хорошо известные функции или конструкции подробно не описываются, чтобы не загромождать сущность изобретения ненужными деталями.
Настоящее изобретение обеспечивает способ вычисления многомерных значений мягкого решения, необходимых в качестве входных сигналов канального декодера, из двумерного принятого сигнала, с использованием процедуры метрики двойного минимума.
В передатчике модулятор делит выходной битовый поток канального кодера на m-битовые сигнальные последовательности и отображает сигнальные последовательности на соответствующие сигнальные точки из М(=2m) сигнальных точек согласно правилу кодирования кодом Грея. Это может быть представлено следующим образом:
Уравнение (1)
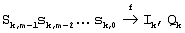
В уравнении (1) sk,i (i=0, 1,… ,m-1) обозначает i-й бит в сигнальной последовательности, отображаемой на k-й символ, a Ik и Qk обозначают синфазную (I) и квадратурную (Q) сигнальные составляющие k-го символа соответственно. Для 8-ричной ФМ m=3, и соответствующая совокупность сигналов представлена на фиг.1. Как показано на чертеже, совокупность сигналов содержит 8 (=23) точек отображения, причем каждая точка имеет разность фаз 45° относительно соседних с ней точек отображения.
Как показано на фиг.1, символ отображается на синфазную сигнальную составляющую Ik и квадратурную сигнальную составляющую Qk и передается в приемник через среду передачи. После приема синфазной сигнальной составляющей и квадратурной сигнальной составляющей приемник демодулирует принятые сигнальные составляющие в демодуляторе символов. Принятый сигнал, соответствующий переданному сигналу, содержащему синфазную сигнальную составляющую Ik и квадратурную сигнальную составляющую Qk, может быть выражен в комплексной записи согласно приведенному ниже уравнению (2), с учетом коэффициента передачи и шумов.
Уравнение (2)
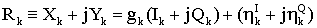
В уравнении (2) Xk и Yk обозначают синфазную сигнальную составляющую и квадратурную сигнальную составляющую двумерного принимаемого сигнала, отображаемого на k-й символ соответственно. Кроме того, gk – комплексный коэффициент, обозначающий коэффициенты передачи передатчика, среды передачи и приемника. Кроме того, 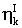 и и 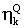 – гауссовские шумы с нулевым средним значением и дивергенцией – гауссовские шумы с нулевым средним значением и дивергенцией 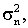 причем эти шумы статистически независимы друг от друга. причем эти шумы статистически независимы друг от друга.
Демодулятор символов приемника вычисляет LLP с использованием принятого сигнала Rk по уравнению (2). Значение LLP, соответствующее i-му биту sk,i (i=0, 1,… ,m-1) в выходной последовательности канального кодера в передатчике, может быть вычислено с помощью уравнения (3), и вычисленное значение LLP подается на канальный декодер в приемнике в виде значения мягкого решения.
Уравнение(3)
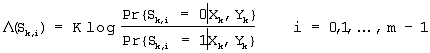
В уравнении (3)  (sk,i) есть LLP или значение мягкого решения, соответствующее sk,i, k – постоянная, Pr{A|B} – условная вероятность, определенная как вероятность того, что событие А возникнет при условии, что возникает условие В. Однако уравнение (3) является нелинейным, требуя относительно больших вычислений. Поэтому необходимо аппроксимировать уравнение (3) для действительной реализации. В случае каналов с гауссовым шумом при gk=1 в уравнении (2) уравнение (3) может быть записано следующим образом. (sk,i) есть LLP или значение мягкого решения, соответствующее sk,i, k – постоянная, Pr{A|B} – условная вероятность, определенная как вероятность того, что событие А возникнет при условии, что возникает условие В. Однако уравнение (3) является нелинейным, требуя относительно больших вычислений. Поэтому необходимо аппроксимировать уравнение (3) для действительной реализации. В случае каналов с гауссовым шумом при gk=1 в уравнении (2) уравнение (3) может быть записано следующим образом.
Уравнение (4)
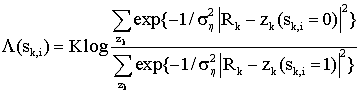
Однако уравнение (4) также нелинейно. Поэтому уравнение (4) может быть аппроксимировано путем процедуры метрики двойного минимума, предложенной Motorola, в следующем виде:
Уравнение (5)
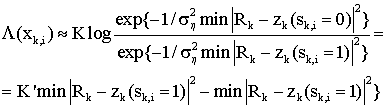
В уравнении (5) K’=(1/ n 2)K и zk(sk,i=0) и zk(sk,i=1) указывают на действительные значения Ik+jQk для sk,i=0 и sk,i=1 соответственно. Чтобы вычислить уравнение (5), необходимо определить zk(sk,i=0) и zk(sk,i=1) для минимизации |Rk-zk(sk,i=0)|2 и |Rk-zk(sk,z=1)|2 для двумерного принятого сигнала Rk. n 2)K и zk(sk,i=0) и zk(sk,i=1) указывают на действительные значения Ik+jQk для sk,i=0 и sk,i=1 соответственно. Чтобы вычислить уравнение (5), необходимо определить zk(sk,i=0) и zk(sk,i=1) для минимизации |Rk-zk(sk,i=0)|2 и |Rk-zk(sk,z=1)|2 для двумерного принятого сигнала Rk.
Учитывая nk,i, указывающее на значение i-го бита последовательности восстановления для сигнальной точки, ближайшей к Rk, и 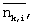 указывающее на логическую операцию отрицания для nk,i, уравнение (5) можно переписать в следующем виде: указывающее на логическую операцию отрицания для nk,i, уравнение (5) можно переписать в следующем виде:
Уравнение (6)
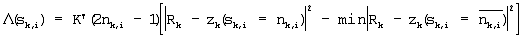
Т.е. уравнение (6) может быть вычислено путем определения того, равно ли значение nk,i i-го бита последовательности восстановления для сигнальной точки на кратчайшем расстоянии от Rk значению “0” или “1”, и определения минимального значения 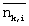 для значения i-го бита последовательности восстановления. Значение, вычисленное посредством уравнения (6), становится значением мягкого решения для значения i-го бита последовательности восстановления. По мере того как значение мягкого решения становится больше по положительному или отрицательному значению, информация, поданная на канальный декодер, становится более корректной. для значения i-го бита последовательности восстановления. Значение, вычисленное посредством уравнения (6), становится значением мягкого решения для значения i-го бита последовательности восстановления. По мере того как значение мягкого решения становится больше по положительному или отрицательному значению, информация, поданная на канальный декодер, становится более корректной.
Сигнальная точка на кратчайшем расстоянии от Rk определяется диапазонами значения синфазной сигнальной составляющей и значения квадратурной сигнальной составляющей Rk. Поэтому первый
член в скобках уравнения (6) может быть записан следующим образом:
Уравнение (7)
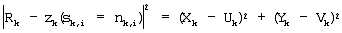
В уравнении (7) Uk и Vk обозначают синфазную сигнальную составляющую и квадратурную сигнальную составляющую сигнальной точки, отображенной посредством nk={nk,m-1,… ,nk,i,… ,nk,1, nk,0} соответственно.
Кроме того, второй член в скобках в уравнении (6) может быть записан в следующем виде:
Уравнение (8)
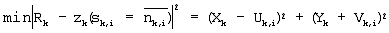
В уравнении (8) Uk,i и Vk,i обозначают синфазную сигнальную составляющую и квадратурную сигнальную составляющую сигнальной точки, отображенной посредством последовательности восстановления 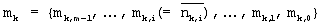 для zk, минимизирующего для zk, минимизирующего 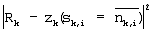 соответственно. Уравнение (6) записывается как уравнение (9) с помощью уравнений (7) и (8) в следующем виде: соответственно. Уравнение (6) записывается как уравнение (9) с помощью уравнений (7) и (8) в следующем виде:
Уравнение (9)
 (sk,i)=K'(2nk,i-1)[{(Xk-Uk)2+(Yk-Vk)2}-{(Xk-Uk,i)2+(Yk-Vk,i)2}]= (sk,i)=K'(2nk,i-1)[{(Xk-Uk)2+(Yk-Vk)2}-{(Xk-Uk,i)2+(Yk-Vk,i)2}]=
=K'(2nk,i-1)[(Uk+Uk,i-2Xk)(Uk-Uk,i)+(Vk+Vk,i-2Yk)(Vk-Vk,i)]
Из уравнения (9) может быть вычислено m значений мягкого решения, необходимых в качестве входных значений канального декодера, поддерживающего m-уровневую модуляцию.
Ниже описан способ вычисления входных значений мягкого решения для канального декодера в демодуляторе системы передачи данных, использующей 8-ричную ФМ, согласно уравнению (9).
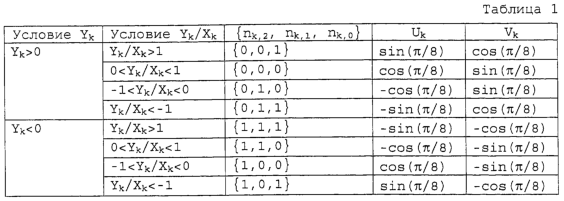
Сначала используется Таблица 1 для вычисления {nk,2, nk,1, nk,0}, Uk, Vk из двух сигнальных составляющих Xk и Yk модулированного 8-ричной ФМ принятого сигнала Rk. Таблица 1 иллюстрирует {nk,2, nk,1, nk,0}, Uk и Vk для случая, где принятый сигнал Rk возникает в каждой из 8 областей с центрами в сигнальных точках, показанных на фиг.1. Для удобства, в Таблице 1 опущены 4 граничные значения, т.е. результирующие значения при Xk=0, Yk=0, Yk=Xk, Yk=-Xk.
Кроме того, Таблица 2 иллюстрирует последовательность {mk,2,mk,1,mk,0}, минимизирующую 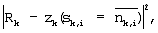 вычисленную для i (где i вычисленную для i (где i {0,1,2}), в терминах функции {nk,2, nk,1, nk,0}, а также иллюстрирует синфазную и квадратурную сигнальные составляющие Uk,i и Vk,i соответствующего zk. {0,1,2}), в терминах функции {nk,2, nk,1, nk,0}, а также иллюстрирует синфазную и квадратурную сигнальные составляющие Uk,i и Vk,i соответствующего zk.
| Таблица 2 |
| i |
{mk,2,mk,i,mk,0} |
Uk,i |
Vk,i |
| 2 |
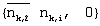 |
Uk,2 |
Vk,2 |
| 1 |
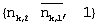 |
Uk,1 |
Vk,1 |
| 0 |
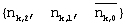 |
Uk,0 |
Vk,0 |
Таблица 3 иллюстрирует Uk,i и Vk,i соответствующие {mk,2,mk,1,mk,0}, определенным из Таблицы 2 для всех комбинаций {nk,2, nk,1, nk,0}.
| Таблица 3 |
| {nk,2,nk,1,nk,0} |
Uk,2 |
Uk,1 |
Uk,0 |
Vk,2 |
Vk,1 |
Vk,0 |
| {0,0,1} |
cos( /8) /8) |
-sin( /8) /8) |
cos( /8) /8) |
-sin( /8) /8) |
cos( /8) /8) |
sin( /8) /8) |
| {0,0,0} |
cos( /8) /8) |
-sin( /8) /8) |
sin( /8) /8) |
-sin( /8) /8) |
cos( /8) /8) |
cos( /8) /8) |
| {0,1,0} |
-cos( /8) /8) |
sin( /8) /8) |
-sin( /8) /8) |
-sin( /8) /8) |
cos( /8) /8) |
cos( /8) /8) |
| {0,1,1} |
-cos( /8) /8) |
sin( /8) /8) |
-cos( /8) /8) |
-sin( /8) /8) |
cos( /8) /8) |
sin( /8) /8) |
| {1,1,1} |
-cos( /8) /8) |
sin( /8) /8) |
-cos( /8) /8) |
sin( /8) /8) |
-cos( /8) /8) |
-sin( /8) /8) |
| {1,1,0} |
-cos( /8) /8) |
sin( /8) /8) |
-sin( /8) /8) |
sin( /8) /8) |
-cos( /8) /8) |
-cos( /8) /8) |
| {1,0,0} |
cos( /8) /8) |
-sin( /8) /8) |
sin( /8) /8) |
sin( /8) /8) |
-cos( /8) /8) |
-cos( /8) /8) |
| {1,0,1} |
cos( /8) /8) |
-sin( /8) /8) |
cos( /8) /8) |
sin( /8) /8) |
-cos( /8) /8) |
-sin( /8) /8) |
Таблица 4 иллюстрирует результаты, полученные путем масштабирования с понижением в отношении 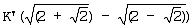 для значений мягкого решения, полученных путем подстановки Uk,i и Vk,i из Таблицы 3 в уравнение (9), т.е. иллюстрирует результаты, нормированные посредством для значений мягкого решения, полученных путем подстановки Uk,i и Vk,i из Таблицы 3 в уравнение (9), т.е. иллюстрирует результаты, нормированные посредством 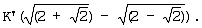 Т.е. когда применяется принятый сигнал Rk, то может быть определено LLR, удовлетворяющее соответствующему условию, как значение мягкого решения по Таблице 4. Если канальный декодер, использованный в системе, не является декодером логарифмической максимальной апостериорной вероятности, то должен быть добавлен процесс масштабирования с повышением LLR по Таблице 4 в реверсивном отношении к отношению масштабирования с понижением. Т.е. когда применяется принятый сигнал Rk, то может быть определено LLR, удовлетворяющее соответствующему условию, как значение мягкого решения по Таблице 4. Если канальный декодер, использованный в системе, не является декодером логарифмической максимальной апостериорной вероятности, то должен быть добавлен процесс масштабирования с повышением LLR по Таблице 4 в реверсивном отношении к отношению масштабирования с понижением.

Однако при выполнении демодуляции мягкого решения 8-ричной ФМ с использованием Таблицы 4 демодулятор должен сначала выполнять операцию определения условия, включающую операцию деления, по двум составляющим принятого сигнала. После этого демодулятор выбирает формулу, соответствующую результату операции определения условия среди формул, указанных соответственно условиям, и подставляет две составляющие принятого сигнала в выбранную формулу, тем самым вычисляя значения мягкого решения. С этой целью демодулятор требует использования оператора для выполнения операции деления и памяти для хранения различных формул, соответствующих условию.
Для исключения операции деления и устранения необходимости в памяти, необходимо модифицировать формулы определения условия и формулы вычисления значения мягкого решения, чтобы можно было применять их одинаковым образом даже к различным условиям. С этой целью формулы определения условия, показанные в Таблице 4, могут быть выражены, как показано в Таблице 5, с использованием новой функции Zk, определенной как |Xk|-|Yk|. В Таблице 5 операции деления исключены, и значения мягкого решения для 4 граничных значений, которые для удобства были опущены в Таблице 4, здесь приняты во внимание.

В реализации на основе аппаратных средств Таблица 5 может быть упрощена в виде Таблицы 6 при условии, что знак Xk, Yk и Zk может быть выражен посредством их наиболее значимого бита (MSB) или знакового бита. В Таблице 6 MSB(x) обозначает наиболее значимый бит данного значения х.
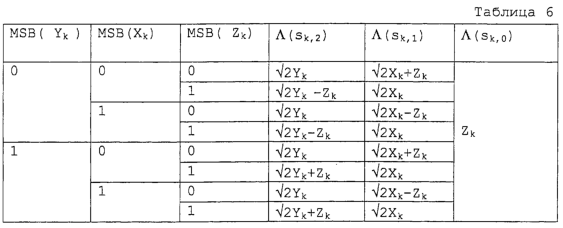
Из Таблицы 6 значения мягкого решения  (sk,2), (sk,2),  (sk,1) и (sk,1) и  (sk,0) для каждого i выражаются следующим образом: (sk,0) для каждого i выражаются следующим образом:
Уравнение (10)
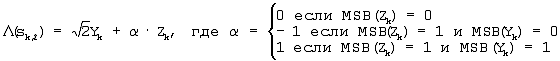
В уравнении (10) параметр  равен 0 для MSB(Zk)=0; -1 для MSB(Zk)=1 и MSB(Yk)=0; и 1 для MSB(Zk)=1 и MSB(Yk)=1. равен 0 для MSB(Zk)=0; -1 для MSB(Zk)=1 и MSB(Yk)=0; и 1 для MSB(Zk)=1 и MSB(Yk)=1.
Уравнение (11)
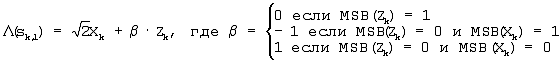
В уравнении (11) параметр  равен 0 для MSB(Zk)=1; -1 для MSB(Zk)=0 и MSB(Xk)=1; и 1 для MSB(Zk)=0 и MSB(Xk)=0. равен 0 для MSB(Zk)=1; -1 для MSB(Zk)=0 и MSB(Xk)=1; и 1 для MSB(Zk)=0 и MSB(Xk)=0.
Уравнение (12)
 (Sk,0)=Zk (Sk,0)=Zk
Т.е. в цифровой системе связи, использующей 8-ричную ФМ, возможно действительно вычислить 3 значения мягкого решения, которые являются выходными сигналами демодулятора для одного принятого сигнала или входными сигналами канального декодера, с использованием процедуры метрики двойного минимума по уравнению (4), путем простых вычислительных формул согласно уравнениям (10)-(12). Этот процесс иллюстрируется на фиг.2.
На фиг.2 показана процедура для вычисления значений мягкого решения в цифровой системе связи, использующей 8-ричную ФМ согласно возможному варианту осуществления настоящего изобретения. Согласно фиг.2 на этапе S110 демодулятор символов вычисляет Zk=|Xk|-|Yk| для определения формул, определяющих условия, показанные в Таблице 4 как новая функция. Демодулятор символов анализирует MSB для Zk на этапе S120, чтобы определить  и и  в соответствии с MSB в Zk в уравнениях (1)-(12). В результате анализа на этапе S120, если MSB в Zk равен “0”, то демодулятор символов переходит к этапу S130, а в противном случае переходит к этапу S140. На этапе S130 демодулятор символов анализирует MSB в Xk. В результате анализа на этапе S130, если MSB в Хk равен “1”, то демодулятор символов устанавливает параметр в соответствии с MSB в Zk в уравнениях (1)-(12). В результате анализа на этапе S120, если MSB в Zk равен “0”, то демодулятор символов переходит к этапу S130, а в противном случае переходит к этапу S140. На этапе S130 демодулятор символов анализирует MSB в Xk. В результате анализа на этапе S130, если MSB в Хk равен “1”, то демодулятор символов устанавливает параметр  на “0” и параметр на “0” и параметр  на “-1” на этапе S150. Если MSB в Хk равен “0”, то демодулятор символов устанавливает параметр на “-1” на этапе S150. Если MSB в Хk равен “0”, то демодулятор символов устанавливает параметр  на “0” и параметр на “0” и параметр  на “1” на этапе S160. на “1” на этапе S160.
В результате анализа на этапе S120, если MSB в Zk равен “1”, то демодулятор символов на этапе S140 анализирует MSB в Yk. В результате анализа на этапе S140, если MSB в Yk равен “0”, то демодулятор символов устанавливает параметр  на “-1” и параметр на “-1” и параметр  на “0” на этапе S170. Если MSB в Yk равен “1”, то демодулятор символов устанавливает параметр на “0” на этапе S170. Если MSB в Yk равен “1”, то демодулятор символов устанавливает параметр  на “1” и параметр на “1” и параметр  на “0” на этапе S180. После этого на этапе S190 демодулятор символов вычисляет значения мягкого решения путем подстановки параметров на “0” на этапе S180. После этого на этапе S190 демодулятор символов вычисляет значения мягкого решения путем подстановки параметров  и и  , определенных на предыдущих этапах, и принятого сигнала в уравнения (10)-(12). Таким путем выполняется демодуляция символов. , определенных на предыдущих этапах, и принятого сигнала в уравнения (10)-(12). Таким путем выполняется демодуляция символов.
Таким образом, процесс вычисления значений мягкого решения по процедуре метрики двойного минимума включает первый этап определения первого параметра  и второго параметра и второго параметра  путем анализа двумерного принятого сигнала, содержащего синфазную составляющую и квадратурную составляющую, и второй этап вычисления значений мягкого решения с использованием двумерного принятого сигнала и первого параметра путем анализа двумерного принятого сигнала, содержащего синфазную составляющую и квадратурную составляющую, и второй этап вычисления значений мягкого решения с использованием двумерного принятого сигнала и первого параметра  и второго параметра и второго параметра  , определенных на первом этапе. Полученные значения мягкого решения демодулированного символа подаются на канальный декодер. , определенных на первом этапе. Полученные значения мягкого решения демодулированного символа подаются на канальный декодер.
На фиг.3 показан вычислитель для определения значений мягкого решения демодулированного символа соответственно возможному варианту осуществления настоящего изобретения. Согласно фиг.3 вычислитель для определения значений мягкого решения по процедуре метрики двойного минимума в цифровой системе связи содержит анализатор 10 принятого сигнала и блок 20 выдачи значений мягкого решения. Анализатор 10 принятого сигнала определяет первый параметр  и второй параметр и второй параметр  путем анализа двумерного принятого сигнала, содержащего синфазную сигнальную составляющую Xk и квадратурную сигнальную составляющую Yk. Блок 20 выдачи значений мягкого решения затем вычисляет значения мягкого решения путем анализа двумерного принятого сигнала, содержащего синфазную сигнальную составляющую Xk и квадратурную сигнальную составляющую Yk. Блок 20 выдачи значений мягкого решения затем вычисляет значения мягкого решения  (sk,2), (sk,2),  (sk,1) и (sk,1) и  (Sk,0), требуемые для декодирования мягкого решения, с использованием принятого сигнала и определенных параметров (Sk,0), требуемые для декодирования мягкого решения, с использованием принятого сигнала и определенных параметров  и и  . .
Логическая схема вычислителя для вычисления значений мягкого решения в соответствии с уравнениями (10)-(12) показана на фиг.4. В частности, на фиг.4 показан вычислитель значения мягкого решения для использования в цифровой системе связи, использующей 8-ричную ФМ. Логическая схема по фиг.4 включена в демодулятор цифровой системы связи, использующей 8-ричную ФМ, и вычисляет значения мягкого решения с использованием уравнений (10)-(12). Здесь двумерный принятый сигнал Rk, синфазная сигнальная составляющая Xk и квадратурная сигнальная составляющая Yk, переменная Zk, параметр  и параметр и параметр  все являются действительными числами и цифровыми значениями со знаковым битом. На фиг.4 вычислитель 105, инвертор 115, первый блок 155 выделения MSB, первый селектор 110, третий блок 165 выделения MSB и третий селектор 120 образуют структуру для определения первого параметра все являются действительными числами и цифровыми значениями со знаковым битом. На фиг.4 вычислитель 105, инвертор 115, первый блок 155 выделения MSB, первый селектор 110, третий блок 165 выделения MSB и третий селектор 120 образуют структуру для определения первого параметра  . Кроме того, вычислитель 105, инвертор 115, второй блок 160 выделения MSB, второй селектор 135, третий блок 165 выделения MSB и четвертый селектор 140 образуют структуру для определения параметра . Кроме того, вычислитель 105, инвертор 115, второй блок 160 выделения MSB, второй селектор 135, третий блок 165 выделения MSB и четвертый селектор 140 образуют структуру для определения параметра  . .
В соответствии с фиг.4 вычислитель 105 вычисляет Zk=|Xk|-|Yk| с использованием синфазной сигнальной составляющей Xk и квадратурной сигнальной составляющей Yk двумерного принятого сигнала Rk, отображенного на k-й символ. Инвертор 115 инвертирует знак Zk путем умножения Zk с вычислителя 105 на “-1”. Первый блок 155 выделения MSB выделяет MSB принятого Yk и выдает выделенный MSB на первый селектор 110 в качестве первого выбранного сигнала. Второй блок 160 выделения MSB выделяет MSB принятого Xk и выдает выделенный MSB на второй селектор 135 в качестве второго выбранного сигнала. Третий блок 165 выделения MSB выделяет MSB Zk, принятого от вычислителя 105, и выдает выделенный MSB на третий селектор 120 в качестве третьего выделенного сигнала. Кроме того, Yk умножается на 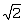 в первом умножителе 130 и Xk также умножается на в первом умножителе 130 и Xk также умножается на 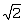 во втором умножителе 150. во втором умножителе 150.
Первый селектор 110 принимает Zk от вычислителя 105 и -Zk от инвертора 115 и выбирает один из этих входных сигналов соответственно первому выбранному сигналу с первого блока 155 выделения MSB. Третий селектор 120 затем принимает выходной сигнал первого селектора 110 и бит “0” и выбирает один из входных сигналов соответственно третьему выбранному сигналу с третьего блока 165 выделения MSB. Выходной сигнал третьего селектора 120 суммируется с выходным значением 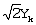 первого умножителя 130 посредством первого сумматора 125, формируя третье значение мягкого решения первого умножителя 130 посредством первого сумматора 125, формируя третье значение мягкого решения  (Sk,2) принятого сигнала Rk, отображенного на k-й символ. (Sk,2) принятого сигнала Rk, отображенного на k-й символ.
Кроме того, второй селектор 135 принимает Zk от вычислителя 105 и -Zk от инвертора 115 и выбирает один из этих входных сигналов соответственно второму выбранному сигналу с второго блока 160 выделения MSB. Четвертый селектор 140 затем принимает выходной сигнал второго селектора 135 и бит “0” и выбирает один из этих входных сигналов соответственно третьему выбранному сигналу с третьего блока 165 выделения MSB. Выходной сигнал четвертого селектора 140 суммируется с выходным значением 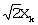 второго умножителя 150 посредством второго сумматора 145, формируя второе значение мягкого решения второго умножителя 150 посредством второго сумматора 145, формируя второе значение мягкого решения  (sk,1) принятого сигнала Rk, отображенного на k-й символ. (sk,1) принятого сигнала Rk, отображенного на k-й символ.
При этом выходное значение Zk вычислителя 105 становится первым значением мягкого решения  (sk,0) принятого сигнала Rk, отображенного на k-й символ. (sk,0) принятого сигнала Rk, отображенного на k-й символ.
В соответствии с предшествующим описанием обычный вычислитель значения мягкого решения, использующий процедуру метрики двойного минимума, реализуемую уравнением (5), требует десять и более операций возведения в квадрат и сравнения. Однако новый вычислитель по фиг.4, реализованный с использованием уравнений (10)-(12), содержит три сумматора, 3 умножителя и 4 мультиплексора, что способствует заметному сокращению времени работы и сложности вычислителя. Таблица 7 иллюстрирует сравнение между уравнением (5) и уравнениями (10)-(12) в терминах типа и числа операций для i {0,1,2}. {0,1,2}.
| Таблица 7 |
| Уравнение (4) |
Уравнения (10)-(12) |
| Операция |
Кол-во операций |
Операция |
Кол-во операций |
| Суммирование |
3× 8+3=27 |
Суммирование |
3 |
| Возведение в квадрат |
2× 8=16 |
Умножение |
3 |
| Сравнение |
3× 2× 3=18 |
Муль типлексирование |
4 |
Ниже проведено сравнение между обычным способом вычисления значения  (sk,2) с использованием уравнения (5) и новым способом вычисления значения (sk,2) с использованием уравнения (5) и новым способом вычисления значения  (sk,2) с использованием уравнения (10). На фиг.5 показана совокупность сигналов, имеющая точки отображения соответственно 8-ричной ФМ, для пояснения вычислений. Согласно фиг.5 двумерный принятый сигнал Rk, содержащий синфазную сигнальную составляющую Xk и квадратурную сигнальную составляющую Yk, имеет значение координаты, представленное “х”. Здесь предполагается, что Xk=-0,6 и Yk=-0,1. (sk,2) с использованием уравнения (10). На фиг.5 показана совокупность сигналов, имеющая точки отображения соответственно 8-ричной ФМ, для пояснения вычислений. Согласно фиг.5 двумерный принятый сигнал Rk, содержащий синфазную сигнальную составляющую Xk и квадратурную сигнальную составляющую Yk, имеет значение координаты, представленное “х”. Здесь предполагается, что Xk=-0,6 и Yk=-0,1.
Сначала описан обычный процесс вычисления значения  (sk,2) с использованием уравнения (5). (sk,2) с использованием уравнения (5).
Для определения кратчайшего расстояния сначала рассчитывается квадрат каждого расстояния между принятым сигналом Rk и 4 отображающими точками при sk,2=1 (т.е. 4 отображающие точки ниже оси х на фиг.5).
Квадрат расстояния от отображающей точки “110”={-0,6-cos(9 /8)}2+{-0,1-sin(9 /8)}2+{-0,1-sin(9 /8)}2=0,185 /8)}2=0,185
Квадрат расстояния от отображающей точки “111”={-0,6-cos(11 /8)}2+{-0,1-sin(11 /8)}2+{-0,1-sin(11 /8)}2=0,726 /8)}2=0,726
Квадрат расстояния от отображающей точки “101”={-0,6-cos(13 /8)}2+{-0,1-sin(13 /8)}2+{-0,1-sin(13 /8)}2=1,644 /8)}2=1,644
Квадрат расстояния от отображающей точки “100”={-0,6-cos(15 /8)}2+{-0,1-sin(15 /8)}2+{-0,1-sin(15 /8)}2=2,402 /8)}2=2,402
Поэтому минимальное значение (или кратчайшее расстояние от принятого сигнала Rk) |Rk-zk(sk,2=1)|2 равно 0,185.
Затем для определения кратчайшего расстояния сначала рассчитывается квадрат каждого расстояния между принятым сигналом Rk и 4 отображающими точками при sk,2=0 (т.е. 4 отображающие точки выше оси х на фиг.5).
Квадрат расстояния от отображающей точки “000”={-0,6-cos( /8)}2+{-0,1-sin( /8)}2+{-0,1-sin( /8)}2=2,555 /8)}2=2,555
Квадрат расстояния от отображающей точки “001”={-0,6-cos(3 /8)}2+{-0,1-sin(3 /8)}2+{-0,1-sin(3 /8)}2=2,014 /8)}2=2,014
Квадрат расстояния от отображающей точки “011”={-0,6-cos(5 /8)}2+{-0,1-sin(5 /8)}2+{-0,1-sin(5 /8)}2=1,096 /8)}2=1,096
Квадрат расстояния от отображающей точки “010”={-0,6-cos(7 /8)}2+{-0,1-sin(7 /8)}2+{-0,1-sin(7 /8)}2=0,338 /8)}2=0,338
Поэтому минимальное значение |Rk-zk(sk,2=1)|2 равно 0,338.
Если полученные выше результаты подставить в уравнение (5), то значение мягкого решения будет получено как
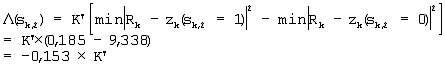
Далее описан новый процесс вычисления значения  (sk,2) с использованием уравнения (10). (sk,2) с использованием уравнения (10).
Сначала вычисляются Zk и  . .
Zk=|Xk|-|Yk|=|-0,6|-|-0,1|=0,5
Отсюда, поскольку Zk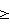 0, т.е. MSB(Zk)=0, 0, т.е. MSB(Zk)=0,  =0. =0.
Если вышеприведенные результаты подставить в уравнение (10), то значение мягкого решения будет иметь вид:
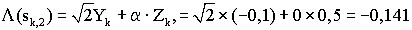
То, что результат уравнения (5) отличается от результата уравнения (10), объясняется тем, что значение мягкого решения, вычисленное по уравнению (9), было нормировано посредством 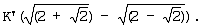 В случае турбокодера, использующего ядро максимума логарифмической апостериорной вероятности (в настоящее время как L3QS, так и 1× TREME используют ядро максимума логарифмической апостериорной вероятности) нормировка всех значений LLP (или мягких значений) с использованием одного и того же коэффициента никогда не оказывает влияния на рабочие характеристики. В случае турбокодера, использующего ядро максимума логарифмической апостериорной вероятности (в настоящее время как L3QS, так и 1× TREME используют ядро максимума логарифмической апостериорной вероятности) нормировка всех значений LLP (или мягких значений) с использованием одного и того же коэффициента никогда не оказывает влияния на рабочие характеристики.
Если некоторый коэффициент в действительности умножается для вычисления ненормированного значения, то
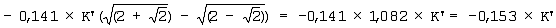
Следует отметить, что вычисленное ненормированное значение идентично результату уравнения (5).
Таким образом, чтобы сократить временную задержку и сложность, обусловленные использованием процедуры метрики двойного минимума по уравнению (5), настоящее изобретение предусматривает пропускание таблиц отображения (Таблиц 4-6) через процесс обработки по уравнениям (6)-(9) и Таблицам 1-3. Кроме того, настоящее изобретение предусматривает подстановку таблиц отображения в уравнения (10)-(12), представляющие формулы, реализующие процедуру метрики двойного минимума. Кроме того, настоящее изобретение предусматривает логическую схему вычислителя для вычисления мягких значений 8-ричной ФМ, реализуемую согласно уравнениям (10)-(12).
Как описано выше, при получении значения мягкого решения, необходимого в качестве входного для канального декодера в процедуре метрики двойного минимума, новый демодулятор для цифровой системы связи, использующей модуляцию посредством 8-ричной ФМ, обеспечивает простые и быстрые вычисления, в значительной мере способствуя уменьшению рабочего времени и сложности демодулятора, который вычисляет значения мягкого решения.
Хотя изобретение показано и описано со ссылками на его предпочтительный вариант осуществления, следует иметь в виду, что специалистами в данной области техники могут быть сделаны различные изменения по форме и в деталях без отклонения от сущности и объема изобретения, как представлено в формуле изобретения.
Формула изобретения
1. Устройство демодуляции сигналов 8-ричной фазовой манипуляции (ФМ) для приема входного сигнала Rk(Xk,Yk), содержащего k-ю квадратурную составляющую Yk и k-ю синфазную составляющую Xk, и для генерирования значений  (sk,0), (sk,0),  (sk,1) и (sk,1) и  (sk,2) мягкого решения для входного сигнала Rk(Xk,Yk) с помощью средства мягкого решения, содержащее анализатор принятого сигнала для вычисления функции Zk входного сигнала Rk(Xk,Yk) согласно уравнению Zk=|Xk|-|Yk| и определения первого параметра (sk,2) мягкого решения для входного сигнала Rk(Xk,Yk) с помощью средства мягкого решения, содержащее анализатор принятого сигнала для вычисления функции Zk входного сигнала Rk(Xk,Yk) согласно уравнению Zk=|Xk|-|Yk| и определения первого параметра  и второго параметра и второго параметра  посредством входного сигнала и блок выдачи мягкого решения для вычисления значений мягкого решения для входного сигнала Rk(Xk,Yk) с использованием первого параметра посредством входного сигнала и блок выдачи мягкого решения для вычисления значений мягкого решения для входного сигнала Rk(Xk,Yk) с использованием первого параметра  и второго параметра и второго параметра  и принятого сигнала Rk(Xk,Yk) в соответствии с и принятого сигнала Rk(Xk,Yk) в соответствии с
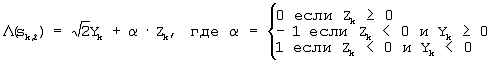
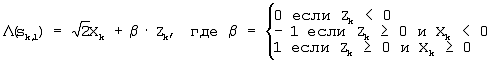
 (sk,0)=Zk (sk,0)=Zk
где  (sk,i) указывает на значение мягкого решения, соответствующее sk,i (i=0, 1, 2), и sk,i указывает на i-й бит в последовательности кодированного сигнала, отображаемый на k-й символ. (sk,i) указывает на значение мягкого решения, соответствующее sk,i (i=0, 1, 2), и sk,i указывает на i-й бит в последовательности кодированного сигнала, отображаемый на k-й символ.
2. Способ демодуляции сигналов 8-ричной фазовой манипуляции (ФМ) для приема входного сигнала Rk(Xk,Yk), содержащего k-ю квадратурную составляющую Yk и k-ю синфазную составляющую Xk, и для генерирования значений  (sk,0), (sk,0),  (sk,1) и (sk,1) и  (sk,2) мягкого решения для входного сигнала Rk(Xk,Yk) с помощью средства мягкого решения, включающий этапы вычисления мягкого значения Zk входного сигнала Rk(Xk,Yk) согласно уравнению Zk=|Xk|-|Yk| и определения первого параметра (sk,2) мягкого решения для входного сигнала Rk(Xk,Yk) с помощью средства мягкого решения, включающий этапы вычисления мягкого значения Zk входного сигнала Rk(Xk,Yk) согласно уравнению Zk=|Xk|-|Yk| и определения первого параметра  и второго параметра и второго параметра  посредством входного сигнала и вычисления значений мягкого решения для входного сигнала Rk(Xk,Yk) с использованием первого параметра посредством входного сигнала и вычисления значений мягкого решения для входного сигнала Rk(Xk,Yk) с использованием первого параметра  и второго параметра и второго параметра  и принятого сигнала Rk(Xk,Yk) в соответствии с и принятого сигнала Rk(Xk,Yk) в соответствии с
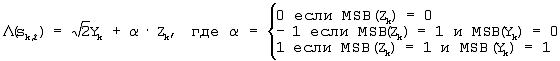
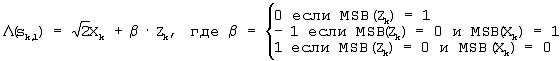
 (sk,0)=Zk (sk,0)=Zk
где  (sk,i) указывает на значение мягкого решения, соответствующее sk,i (i=0, 1, 2), и sk,i указывает на i-й бит в последовательности кодированного сигнала, отображаемый на k-й символ. (sk,i) указывает на значение мягкого решения, соответствующее sk,i (i=0, 1, 2), и sk,i указывает на i-й бит в последовательности кодированного сигнала, отображаемый на k-й символ.
3. Устройство демодуляции сигналов 8-ричной ФМ для приема входного сигнала Rk(Xk,Yk), содержащего k-ю квадратурную составляющую Yk и k-ю синфазную составляющую Xk, и для генерирования значений  (sk,0), (sk,0),  (sk,1) и (sk,1) и  (sk,2) мягкого решения для входного сигнала Rk(Xk,Yk) с помощью средства мягкого решения, содержащее вычислитель для вычисления мягкого значения Zk путем вычитания уровня |Yk| квадратурной сигнальной составляющей Yk из уровня |Xk| синфазной сигнальной составляющей Xk принятого сигнала Rk(Xk,Yk) и выдачи Zk в качестве первого значения мягкого решения; (sk,2) мягкого решения для входного сигнала Rk(Xk,Yk) с помощью средства мягкого решения, содержащее вычислитель для вычисления мягкого значения Zk путем вычитания уровня |Yk| квадратурной сигнальной составляющей Yk из уровня |Xk| синфазной сигнальной составляющей Xk принятого сигнала Rk(Xk,Yk) и выдачи Zk в качестве первого значения мягкого решения;
первый селектор для приема Zk от вычислителя и инвертированного значения -Zk относительно Zk и выбора Zk или -Zk соответственно наиболее значимому биту (MSB) квадратурной сигнальной составляющей Yk;
второй селектор для приема Zk от вычислителя и -Zk и выбора Zk или -Zk соответственно MSB синфазной сигнальной составляющей Xk;
третий селектор для приема выходного сигнала второго селектора и значения “0” и выбора выходного сигнала второго селектора или значения “0” соответственно MSB в Zk;
первый сумматор для суммирования значения, вычисленного путем умножения квадратурной сигнальной составляющей Yk на 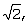 с выходным значением третьего селектора, и выдачи результирующего значения в качестве третьего значения мягкого решения; с выходным значением третьего селектора, и выдачи результирующего значения в качестве третьего значения мягкого решения;
четвертый селектор для приема выходного сигнала второго селектора и значения “0” и выбора выходного сигнала второго селектора или значения “0” соответственно MSB в Zk; и
второй сумматор для суммирования значения, вычисленного путем умножения синфазной сигнальной составляющей Xk на 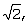 с выходным значением четвертого селектора, и выдачи результирующего значения в качестве второго значения мягкого решения. с выходным значением четвертого селектора, и выдачи результирующего значения в качестве второго значения мягкого решения.
4. Способ демодуляции сигналов 8-ричной ФМ для приема входного сигнала Rk(Xk,Yk), содержащего k-ю квадратурную составляющую Yk и k-ю синфазную составляющую Xk, и для генерирования значений  ( ( k,0), k,0),  ( ( k,1) и k,1) и  ( ( k,2) мягкого решения для входного сигнала Rk(Xk,Yk) с помощью средства мягкого решения, включающий этапы: k,2) мягкого решения для входного сигнала Rk(Xk,Yk) с помощью средства мягкого решения, включающий этапы:
a) вычисления мягкого значения Zk первого демодулированного символа путем вычитания уровня |Yk| квадратурной сигнальной составляющей Yk из уровня |Xk| синфазной сигнальной составляющей Xk принятого сигнала Rk(Xk,Yk),
b) установки первой переменной  на “0”, если мягкое значение Zk имеет положительное значение, установки первой переменной на “0”, если мягкое значение Zk имеет положительное значение, установки первой переменной  на “-1”, если Zk имеет отрицательное значение и квадратурная составляющая Yk имеет положительное значение, и установки первой переменной на “-1”, если Zk имеет отрицательное значение и квадратурная составляющая Yk имеет положительное значение, и установки первой переменной  на “1”, если Zk имеет отрицательное значение и квадратурная составляющая Yk имеет отрицательное значение, на “1”, если Zk имеет отрицательное значение и квадратурная составляющая Yk имеет отрицательное значение,
с) определения мягкого значения третьего демодулированного символа путем вычисления 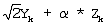 с использованием квадратурной составляющей Yk, мягкого значения Zk и первой переменной с использованием квадратурной составляющей Yk, мягкого значения Zk и первой переменной  ; ;
d) установки второй переменной  на “0”, если мягкое решение Zk имеет отрицательное значение, установки второй переменной на “0”, если мягкое решение Zk имеет отрицательное значение, установки второй переменной  на “-1”, если Zk имеет положительное значение и синфазная составляющая Xk имеет отрицательное значение, и установки второй переменной на “-1”, если Zk имеет положительное значение и синфазная составляющая Xk имеет отрицательное значение, и установки второй переменной  на “1”, если Zk имеет положительное значение и синфазная составляющая Xk имеет положительное значение; на “1”, если Zk имеет положительное значение и синфазная составляющая Xk имеет положительное значение;
е) определения мягкого значения второго демодулированного символа путем вычисления 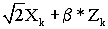 с использованием синфазной составляющей Xk, мягкого значения Zk и второй переменной с использованием синфазной составляющей Xk, мягкого значения Zk и второй переменной  . .
РИСУНКИ
|
|