Патент на изобретение №2253089

(54) СПОСОБ ОПРЕДЕЛЕНИЯ ПЛОЩАДИ РЕЛЬЕФА

(57) Реферат:

Изобретение относится к геодезии и может найти применение при кадастровом учете земельных угодий со сложным рельефом. Сущность: получают массивы цифровых моделей местности аэрокосмическими средствами с высоким пространственным разрешением. Разбивают матрицу ЦММ участка местности на фрагменты с окном |2×2| смежных пикселя. Делят окно диагональю на треугольники. Представляют рельеф мозаикой вписанных треугольников, вершины которых – смежные пиксели ЦММ. Рассчитывают площадь каждого треугольника по теореме Пифагора и формуле Герона. Суммируют площади окон. Технический результат: повышение точности, достоверности, документальности. 5 ил.

Изобретение относится к геодезии и может найти применение при кадастровом учете земельных угодий со сложным рельефом.

Известен аналитический способ определения площади земельных участков [см., например, “Инженерная геодезия” учебник под редакцией Д.Ш.Михелева, Высшая школа, М., 2000 г., стр.335-337 – аналог]. При аналитическом способе определения площадей применяют формулы геометрии, тригонометрии и аналитической геометрии. При этом оцениваемую площадь разбивают на простейшие геометрические фигуры, преимущественно треугольники (прямоугольники), а площадь участка находят как сумму площадей отдельных фигур (S), вычисляемых: для треугольника по двум сторонам l₁, l₂ и углу , заключенному между ними:

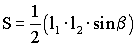
или по формуле Герона:

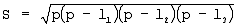
где р – полупериметр сторон треугольника, равный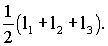

В способе-аналоге площадь участка вычисляют по результатам измерений перечисленных параметров на местности. Результирующая ошибка (стр.337 аналога) определения площади полигона с n вершинами составляет величину

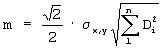
где _x,у – среднеквадратическая ошибка определения координат х, у точек вершин полигона при условии, что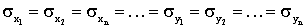

D_i – расстояние от начала координат до i-ой точки вершины полигона. Таким образом, к недостаткам способа-аналога следует отнести:

– увеличение результирующей ошибки при усложнении рельефа, т.е. необходимость разбиения полигона на большее число простейших фигур;

– большой объем, трудоемкость наземных измерений, неоперативность работ;

– трудности реализации способа в сложно-пересеченной и горной местности.

В последние годы совершенствуются методы определения площади земельных участков по цифровым моделям местности (ЦММ). Цифровой моделью местности называют совокупность точек местности с известными координатами в трехмерном пространстве х, у, Н. Существуют различные методы формирования массивов ЦММ, отличающиеся друг от друга различной точностью и степенью детализации элементов рельефа. Точность ЦММ обычно увязывают с требуемой точностью решения инженерно-геодезических задач. При этом рельеф аппроксимируют криволинейными поверхностями различного порядка.

Наиболее универсальными являются статистические модели местности с разделением на фрагменты, каждый из которых приурочивается к определенной форме рельефа: склон, гора, котловина, лощина, седловина, хребет и в пределах которых назначают свой тип аппроксимирующей функции, т.е. рельеф задается многогранной поверхностью [см., например, Н.П.Булгаков, Е.М.Рывина, Г.А.Федотов “Прикладная геодезия” учебник, Недра, М., 1990 г., §16. Математические модели местности, стр.42-44 – ближайший аналог].

В способе ближайшего аналога размещают в районе искомой точки с координатами х, у квадрат или круг, выбирают в их пределах необходимое число исходных точек ЦММ с известными координатами x_m, y_m, H_m и методом наименьших квадратов решают следующую систему уравнений:

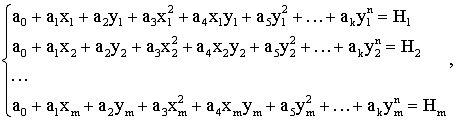
где a₀, а₁… а_k – неизвестные коэффициенты уравнения аппроксимирующей поверхности;

k – число неизвестных коэффициентов;

m – число уравнений.

Как правило, число уравнений при решении системы обычно превышает число неизвестных коэффициентов m>k. Ввиду сложности аналитических решений в практике инженерных расчетов обычно ограничиваются аппроксимирующей поверхностью второго порядка. При получении аналитического выражения Н=Н(х,у) аппроксимирующей поверхности площадь рельефа вычисляют как поверхностный интеграл в области Ф [см., например, Н.С.Пискунов “Дифференциальное и интегральное исчисление для вузов” учебник, 5-е изд., Наука, М., 1964 г., §7. Вычисление площади поверхности, стр.73-74]

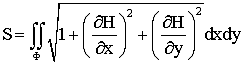
Недостатками ближайшего аналога следует считать:

– используемый метод наименьших квадратов уже предполагает уклонение аппроксимирующих функций от исходных точек ЦММ, т.е. ошибки метода добавляются к ошибкам отсчетов ЦММ;

– сложность вычислительных алгоритмов;

– необходимость последующего вычисления площади поверхности от радикальной функции, т.е., как правило, от неберущегося интеграла.

Задача, решаемая заявляемым способом, состоит в повышении точности путем аппроксимации рельефа мозаикой вписанных треугольников, вершины которых принадлежат соседним отсчетам высот ЦММ, а их площади вычисляются программным расчетом по массиву ЦММ.

Решение поставленной задачи обеспечивается тем, что в способе определения площади рельефа, включающем съемку орбитальным комплексом наблюдения с помощью оптической системы заданных участков, запись полученной информации стереоизображений, по которой определяют цифровую модель местности (ЦММ) в виде массива дискретных отсчетов зависимости высоты Н(х, у) от пространственных координат, разбиение матрицы ЦММ на фрагменты, аналитический расчет поверхности фрагмента как простейшей геометрической фигуры, программным расчетом последовательно, от начала массива, разбивают матрицу на окна из |2× 2| смежных пикселей, делят четырехугольник окна диагоналями на две пары треугольников, представляют рельеф в виде мозаики аппроксимирующих треугольников, по формуле Герона вычисляют площадь каждого треугольника и площадь окна как среднегеометрическое 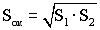площадей S₁, S₂ пар смежных треугольников, а площадь рельефа как сумму площадей окон.

Изобретение поясняется чертежами, где:

фиг.1 – визуализированное изображение участка ЦММ;

фиг.2 – последовательность разбиения матрицы ЦММ на окна;

фиг.3 – разбиение окна диагоналями на две пары смежных треугольников;

фиг.4 – поверхность рельефа, аппроксимированная мозаикой треугольников;

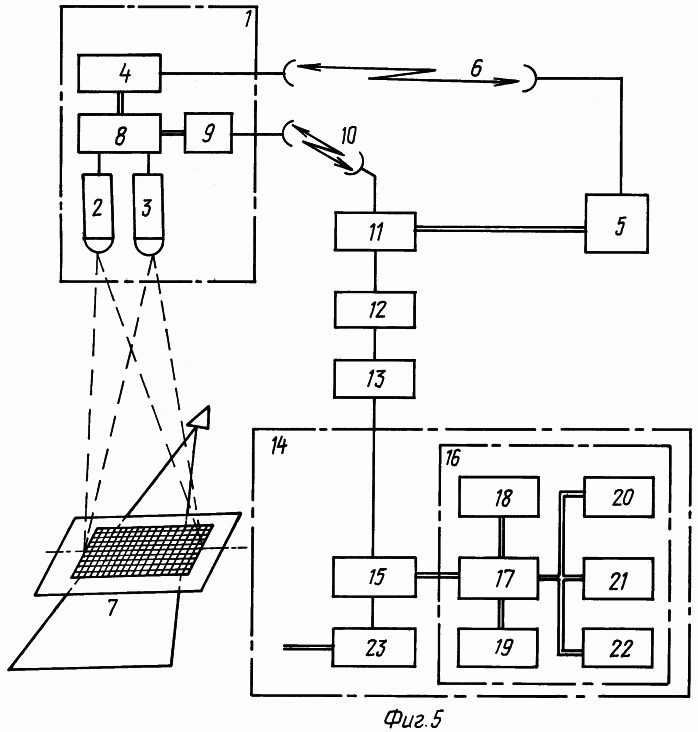
фиг.5 – функциональная схема устройства, реализующая способ.

Техническая сущность изобретения состоит в следующем.

Развитие космических средств наблюдения позволяет в настоящее время получать стереоизображения земной поверхности в видимом диапазоне с разрешением менее 5 м на пиксель. Программные методы обработки стереоизображений [см., например, “Фотограммическая обработка аэроснимков на универсальных стереопарах” в учебнике “Прикладная геодезия”, Н.П.Булгаков, Е.М.Рывкина, Г.А.Федотов, Недра, М., 1990 г., стр.241-247] позволяют формировать цифровые карты местности, широко используемые в военном деле, геодезии, навигации, развитии сотовой связи и др. областях. При наличии ЦММ высокого разрешения представляется возможным решение геодезических задач, в частности вычисление площади рельефа на новом уровне с высокой точностью и документальностью. Цифровая модель местности представляется функцией зависимости высоты Н=Н(х,у) от пространственных координат х, у. На фиг.1 представлено визуализированное изображение ЦММ обрабатываемого участка. На фиг.2 представлена иллюстрация последовательности разбиения матрицы ЦММ на окна их 4-х смежных пикселей. Каждый пиксель ЦММ характеризуется разрешением по координатам x, y, Н, которые считаются известными из технических характеристик средств. Размер участка определяется числом строк и столбцов матрицы. Алгоритм вычисления элементарной площади окна (четырехугольника) основан на триангуляции, т.е. разбиении его диагоналями 1-4 и 3-2 на две пары смежных треугольников. Процедура разбиения иллюстрируется фиг.3. Площадь каждого треугольника вычисляют по формуле Герона. Предварительно, по теореме Пифагора рассчитывают длины сторон треугольников. В соответствии с фиг.3 длины сторон треугольника, например, с вершинами 1-3-4 равны:

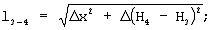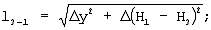
диагональ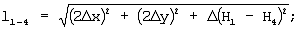

Расчет осуществляют программным методом на ПЭВМ.

Текст программы

program SqrGeron;

const maxx=1000;

var S:real;

ss:string;

st1,st2:array[1..maxx] of byte;

f:text;

i,j,kolx:integer;

dx,dy,dh:real;

procedure SqrSqr(var S:real; x1,x2,y1,y2:real;

h11,h12,h21,h22:byte);

var dS,dS1,dS2:real;

function Geron(x1,y1,h1,x2,y2,h2,x3,y3,h3:real):real;

var 112,123,131,p:real;

begin

112:=sqrt(sqr(x1-x2)+sqr(y1-y2)+sqr(h1-h2));

123:=sqrt(sqr(x2-x3)+sqr(y2-y3)+sqr(h2-h3));

131:=sqrt(sqr(x3-x1)+sqr(y3-y1)+sqr(h3-h1));

p:=(112+123+131)/2;

Geron:=sqrt(p*(p-112)*(p-123)*(p-131));

end;

begin

dS1:=0;

if (h11<>255) and (h12<>255) and (h21<>255) then

dS1:=dS1+Geron(x1,y1,h11*dh,x2,y1,h12*dh,x1,y2,h21*dh);

if (h22<>255) and (h12<>255) and (h21<>255) then

dS1:=dS1+Geron(x2,y2,h22*dh,x2,y1,h12*dh,x1,y2,h21*dh);

dS2:=0;

if (h11<>255) and (h12<>255) and (h22<>255) then

dS2:=dS2+Geron(x1,y1,h11*dh,x2,y1,h12*dh,x2,y2,h22*dh);

if (h22<>255) and (h11<>255) and (h21<>255) then

dS2:=dS2+Geron(x2,y2,h22*dh,x1,y1,h11*dh,x1,y2,h21*dh);

ds:=0;

if dS1>0 then dS:=dS1;

if dS2>0 then dS:=dS2;

if (dS2>0) and (dS2>dS) then dS:=SQRT(dS1*dS2);

S:=S+dS

end;

begin {main}

S:=0;

repeat

writein(‘Enter file name, please’);

readin(ss);

assign(f,ss);

{$I-} reset(f); {$I+}

i:=IOresult;

until i=0;

writeln(‘Enter dx,dy,dh’);

readin(dx,dy,dh);

kolx:=1;

if not eof(f) then

while not eoln(f) or (kolx>maxx) do begin read(f,st1[kolx]); kolx:=kolx+1

end;

if eoln(f) then begin

readin(f);

j:=1;

while not eof(f) do begin

for i:=l to kolx do read(f,st2[i]);

for i:=1 to kolx-1 do

SqrSqr(S,0,dx,0,dy,st1[i],st1[i+1], st2[i],st2[i+1]);

readin(f);

st1:=st2;

j:=j+1;

end;

end else writein(‘Very short array’);

close(f);

assign(f,’result.txt’);

rewrite(f);

writeln(f,’file name – ‘,ss);

writeln(f,’dx=’,dx:10:5,’ dy=’,dy:10:5,’ dh=’,dh:10:5);

writeln(f,’Strok – ‘,j:5,’ Stolb – ‘,kolx);

writeln(f,’Area of region is ‘,S:10:2);

writeln(‘file name – ‘,ss);

writeln(‘dx=’,dx:10:5,’ dy=’,dy:10:5,’ dh=’,dh:10:5);

writeln(‘Strok – ‘,j:5,’ Stolb – ‘,kolx);

writeln(‘Area of region is ‘,S:10:2);

close(f)

end.{main}

Пример реализации способа.

Заявляемый способ может быть реализован на базе устройства по схеме фиг.5. Функциональная схема устройства фиг.5 содержит орбитальный комплекс наблюдения 1 типа космического аппарата (КА) “Ресурс” с установленной на его борту оптической системой стереосъемки типа MOMS-2Р (ФРГ) с каналами 2, 3 формирования стереоизображения. Съемка запланированных участков местности и включение каналов 2, 3 осуществляет бортовой комплекс управления (БКУ) 4 по командам, передаваемым из центра управления полетом (ЦУП) 5 по радиолинии управления 6. Информацию стереоизображений подстилающей поверхности 7 записывают на бортовой видеомагнитофон 8 и в сеансах видимости КА с наземных пунктов сбрасывают, посредством телеметрической системы 9, по автономному каналу связи 10 на наземные пункты приема информации 11, где осуществляется запись массивов информации на видеомагнитофон 12 типа “Арктур”.

Предварительную обработку информации, выделение кадров по служебным признакам и формирование ЦММ осуществляют в Картографическом центре 13 Министерства Природных Ресурсов. Скомпонованные массивы ЦММ по запросам потребителей передаются в Региональные центры кадастрового учета 14, где ведется архив 15 ЦММ региона на базе стримеров типа FT-120. Программный расчет площади рельефа участков осуществляют на ПЭВМ 16 в стандартном наборе элементов: процессора 17, ОЗУ 18, винчестера 19, дисплея 20, принтера 21, клавиатуры 22. Расчетные значения площадей участков помещают в базу региональных данных с выводом на сайт сети “Интернет” 23.

Программу вычисления площади рельефа записывают на винчестер 19. На электронной карте ЦММ высота (глубина) рельефа обычно квантуется в стандартной шкале от 0 до 255 уровней.

Обрабатываемый участок может иметь произвольную конфигурацию. Для его обработки следует выполнить выделение границы участка, “залив” окрестности белым цветом (255). Предполагается, что на обрабатываемом участке максимально возможная высота 255 не достигается. Если это не так, следует использовать изображение местности, выполненное в другом масштабе глубины. Для вычисления площади поверхности обрабатываемого участка необходимо указать масштаб по горизонтали, вертикали и глубине, то есть указать, чему соответствует в метрах один пиксель по горизонтали ( х), по вертикали ( у) и одна единица глубины ( Н).

Для вычисления площади поверхности участка просматривается весь прямоугольник изображения участка с окрестностями последовательно шаблоном из четырех соседних точек, образующих квадрат. Шаблон сканирует изображение слева – направо, сверху – вниз, и для каждого элемента изображения вычисляется элементарная площадь участка, затем все элементарные площади суммируются.

Алгоритм вычисления элементарной площади участка в пределах четырехточечного шаблона основан на триангуляции элемента поверхности. Существуют два способа триангуляции – по главной диагонали (слева-сверху – направо-вниз) и по вспомогательной диагонали (справа-сверху – налево-вниз). Площадь вычисляется обеими способами, в качестве результата выбирается среднегеометрическое. Если хотя бы одна вершина треугольника находится за границей участка – площадь треугольника считается равной нулю. Если все вершины принадлежат участку, площадь треугольника вычисляется по формуле Герона.

Визуализированное изображение обрабатываемой ЦММ представлено на фиг.1. Один пиксель изображения соответствовал 5 м. Пространства х= у=5 м, а единица глубины составляла 7 м.

Число строк изображения ЦММ 490, число столбцов 512. Площадь рельефа 1070 га, площадь проекции рельефа на подошву (основание) 630 га.

Эффективность способа определяется такими показателями, как оперативность, достоверность, документальность, воспроизводимость, точность, стоимость. При использовании аэрокосмических средств получения ЦММ высокого пространственного разрешения преимущества заявляемого способа перед аналогами по перечисленной гамме показателей очевидна.

Формула изобретения

Способ определения площади рельефа, включающий получение цифровой модели местности (ЦММ) в виде массива дискретных отсчетов зависимости высоты Н(х,у) от пространственных координат, разбиение матрицы ЦММ на фрагменты, аналитический расчет поверхности фрагмента как простейшей геометрической фигуры, отличающийся тем, что цифровую модель местности определяют по записанной информации стереоизображений, полученных путем съемки заданных участков орбитальным комплексом наблюдения с помощью оптической системы, по программным расчетам последовательно от начала массива разбивают матрицу на окна из |2×2| смежных пикселей, делят четырехугольник окна диагоналями на две пары треугольников, представляют рельеф в виде мозаики аппроксимирующих треугольников, по формуле Герона вычисляют площадь каждого треугольника и площадь окна как среднегеометрическое 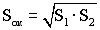площадей S₁, S₂ пар смежных треугольников, а площадь рельефа определяют как сумму площадей окон.

РИСУНКИ

MM4A – Досрочное прекращение действия патента СССР или патента Российской Федерации на изобретение из-за неуплаты в установленный срок пошлины за поддержание патента в силе

Дата прекращения действия патента: 20.02.2006

Извещение опубликовано: 27.10.2007 БИ: 30/2007