|
|
(21), (22) Заявка: 2004100780/28, 08.01.2004
(24) Дата начала отсчета срока действия патента:
08.01.2004
(45) Опубликовано: 10.03.2005
(56) Список документов, цитированных в отчете о
поиске:
SU 256867 A, 16.04.1970. SU 879498 A, 07.11.1981. SU 423066 А, 04.09.1974.
Адрес для переписки:
634050, г.Томск, пр. Ленина, 30, Томский политехнический университет, отдел интеллектуальной и промышленной собственности
|
(72) Автор(ы):
Гольдштейн Е.И. (RU),
Бацева Н.Л. (RU)
(73) Патентообладатель(и):
Томский политехнический университет (RU)
|
(54) СПОСОБ ОПРЕДЕЛЕНИЯ АМПЛИТУДЫ И ФАЗЫ ЭКВИВАЛЕНТНОЙ СИНУСОИДЫ ТОКА В ЦЕПИ С ФЕРРОМАГНИТНЫМ СЕРДЕЧНИКОМ
(57) Реферат:
Способ может быть использован при обработке электротехнических данных для замены действительной несинусоидальной кривой тока, содержащей высшие гармоники, эквивалентной синусоидой. Измеряют мгновенные значения синусоидального питающего напряжения и несинусоидального тока в цепи. По цифровым отсчетам мгновенных значений синусоидального напряжения и несинусоидального тока в цепи, взятых в одни и те же моменты времени, определяют среднюю за период мощность и действующие значения напряжения и тока. Фазу эквивалентной синусоиды определяют по отношению мощности к произведению их действующих значений. 3 ил., 2 табл.
Изобретение относится к области систем обработки информации и электротехники и может быть использовано для замены действительной несинусоидальной кривой тока, содержащей высшие гармоники, эквивалентной синусоидой.
В электротехнике известен способ определения амплитуды и фазы эквивалентной синусоиды [Демирчян К.С. и др. Теоретические основы электротехники /К.С.Демирчян, Л.Р.Нейман, Н.В.Коровкин, В.Л.Чечурин. – 4-е изд., перераб. и доп. СПб.: Питер, 2003. – Т.2], выбранный в качестве прототипа, заключающийся в том, что измеряют мгновенные значения напряжения и тока в цепи, содержащей нелинейные элементы, определяют амплитуду эквивалентной синусоиды тока по формуле 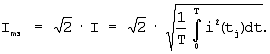
Недостатком известного способа является допущение о том, что не существует угла сдвига  э между синусоидальным напряжением u(tj) и эквивалентной синусоидой тока iэ(tj). э между синусоидальным напряжением u(tj) и эквивалентной синусоидой тока iэ(tj).
Задачей изобретения является разработка способа определения амплитуды и фазы эквивалентной синусоиды тока в цепи с ферромагнитным сердечником по известным синусоидальной кривой напряжения u(tj) и несинусоидальной кривой тока i(tj), представленных цифровьми отсчетами мгновенных значений для одних и тех же моментов времени в однофазной цепи переменного тока.
Это достигается тем, что способ определения амплитуды и фазы эквивалентной синусоиды тока в цепях с ферромагнитным сердечником включает так же, как в прототипе, измерение мгновенных значений синусоидального питающего напряжения u(tj) и несинусоидального тока i(tj) для одних и тех же моментов времени tj=t1,t2,…,tN, где N – число разбиений на периоде Т, и определение амплитуды эквивалентной синусоиды тока по формуле 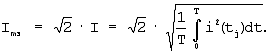
Новым является то, что с помощью программатора действующих значений определяют действующие значения сигналов тока и напряжения по выражениям
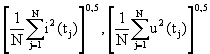
соответственно. Далее с помощью множителя по действующему значению тока определяют амплитуду эквивалентной синусоиды тока по вышеуказанной формуле. Затем с помощью программатора мощности определяют активную (среднюю за период) мощность из выражения
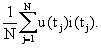
Далее с помощью делителя определяют фазу эквивалентной синусоиды по выражению
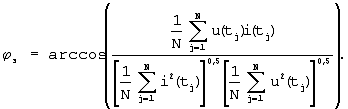
Если в электрической цепи присутствует элемент, имеющий ферромагнитный сердечник, например трансформатор, то периодический ток в такой цепи будет содержать высшие гармоники, даже если приложенное напряжение будет синусоидальным. Для такой цепи дальнейший расчет будет очень сложным из-за невозможности применения векторной диаграммы и комплексной формы записи для сопротивлений, зависящих от тока. Нами экспериментально установлено, что для дальнейшего расчета такой электрической цепи можно заменять несинусоидальную кривую тока эквивалентной синусоидой таким образом, чтобы активная мощность в цепи оставалась без изменения. Активная (средняя за период) мощность может быть определена двояко:
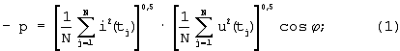
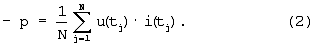
Приравняв правые части формул (1) и (2), можно найти  как как
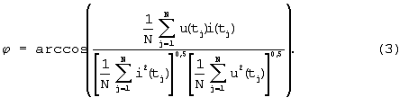
Экспериментально установлено, что формула (3) подходит и для определения эквивалентного угла синусоиды тока, поэтому способ определения амплитуды и фазы эквивалентной синусоиды тока в цепи с ферромагнитным сердечником позволяет определить угол между синусоидальным напряжением и эквивалентной синусоидой тока.
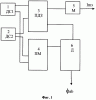
На фиг.1 приведена аппаратная схема устройства, реализующего рассматриваемый способ определения амплитуды и фазы эквивалентной синусоиды тока в цепи с ферромагнитным сердечником.
На фиг.2 приведены графики синусоидального питающего напряжения и несинусоидального тока холостого хода, снятые при опыте холостого хода для трансформатора ПОБС5Г.
На фиг.3 приведены графики синусоидального питающего напряжения и эквивалентной синусоиды тока холостого хода для трансформатора ПОБС5Г.
В табл.1 приведены цифровые отсчеты мгновенных значений синусоидального питающего напряжения и несинусоидального тока холостого хода, снятые при опыте холостого хода для трансформатора ПОБС5Г.
В табл.2 приведены цифровые отсчеты мгновенных значений синусоидального питающего напряжения и эквивалентной синусоиды тока холостого хода для трансформатора ПОБС5Г.
Способ может быть осуществлен с помощью схемы (фиг.1), содержащей датчики сигналов 1 (ДС1), 2 (ДС2), один выход которых соединен с входами программатора действующих значений 3 (ПДЗ), а другой выход с входами программатора мощности 4 (ПМ). Один выход программатора действующих значений 3 (ПДЗ) соединен с входом множителя 5 (М), а другой выход с входом делителя 6 (Д). Выход программатора мощности 4 (ПМ) соединен с входом делителя 6 (Д).
В качестве датчиков сигналов 1 (ДС1) и 2 (ДС2), может быть использован промышленный прибор Базовый информационно-измерительный модуль 2000 (БИМ-1130 С1). Программатор действующих значений 3 (ПДЗ), программатор мощности 4 (ПМ), множитель 5 (М) и делитель 6 (Д) могут быть выполнены на микроконтроллере серии 51 производителя atmel AT89S53. Для работы пользователя может быть предусмотрена кнопочная клавиатура FT008, имеющая 8 кнопок, предназначенных для включения питания, запуска измерения, сохранения значений, и индикатор SCD 55100 для вывода численных значений амплитуды и фазы эквивалентной синусоиды тока.
С выходов датчиков сигналов 1 (ДС1) и 2 (ДС2) сигналы, цифровые отсчеты которых сняты для трансформатора типа ПОБС5Г и представлены в табл.1, а графики, построенные по отсчетам табл.1 – на фиг.2, поступают на входы программатора действующих значений 3 (ПДЗ) и на входы программатора мощности 4 (ПМ) одновременно. С помощью программатора действующих значений 3 (ПДЗ) определяют действующие значения для каждого из сигналов по формуле, заложенной в программатор, а именно
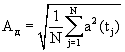
[Гольдштейн Е.И., Коробко П.Ф. Технология решения инженерных задач: Учеб. пособие. – Томск: Изд-во ТПУ, 1999. – 140 с.] Для данных табл.1 – 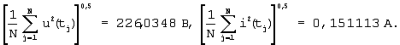 С выхода программатора действующих значений 3 (ПДЗ) действующее значение тока поступает на вход множителя 5 (М). С помощью множителя 5 (М) определяют амплитуду эквивалентной синусоиды по формуле С выхода программатора действующих значений 3 (ПДЗ) действующее значение тока поступает на вход множителя 5 (М). С помощью множителя 5 (М) определяют амплитуду эквивалентной синусоиды по формуле
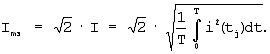
[Демирчян К.С. и др. Теоретические основы электротехники /К.С.Демирчян, Л.Р.Нейман, Н.В.Коровкин, В.Л.Чечурин. – 4-е изд., перераб. и доп. – СПб.: Питер, 2003. Т.2]. В данном случае Imэ=0,213707. С помощью программатора мощности 4 (ПМ) определяют активную (среднюю за период) мощность для этих сигналов по выражению:
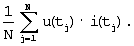
Для данных табл.1 –
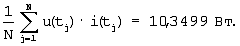
С выхода программатора действующих значений 3 (ПДЗ) действующие значения напряжения и тока поступают на вход делителя 6 (Д). С выхода программатора мощности 4 (ПМ) значение мощности поступает на вход делителя 6 (Д). С помощью делителя 6 (Д) определяют фазу эквивалентной синусоиды по выражению:
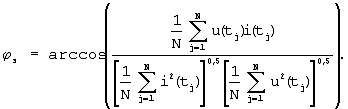
В данном случае  э=72,36149°. э=72,36149°.
Для наглядности в табл.2 представлены цифровые отсчеты мгновенных значений для синусоидального напряжения и эквивалентной синусоиды тока, причем цифровые отсчеты эквивалентной синусоиды тока вычислены для тех же моментов времени, что и цифровые отсчеты синусоидального напряжения, т.е. tj=t1, t2,…, tN. Hа фиг.3 для отсчетов мгновенных значений, приведенных в табл.2, построены графики синусоидального напряжения и эквивалентной синусоиды тока. Сравнивая графики тока на фиг.2 и на фиг.3, видно, что несинусоидальная кривая тока теперь “синусоидальна” и может быть применена для расчетов цепей, содержащих ферромагнитный сердечник.
Таким образом, получен способ определения амплитуды и фазы эквивалентной синусоиды тока в цепи с ферромагнитным сердечником, учитывающий угол сдвига между синусоидальной кривой напряжения и несинусоидальной кривой тока, и может быть использован для построения векторных диаграмм тока и напряжения.
Табл.1
Способ определения амплитуды и фазы эквивалентной синусоиды тока в цепи с ферромагнитным сердечником |
| Время, t, c |
u(tj), В |
I(tj), A |
| 1 |
2 |
3 |
| 0 |
-6,06453 |
-0,25631 |
| 0,0001 |
1,607813 |
-0,24902 |
| 0,0002 |
9,434411 |
-0,24061 |
| 0,0003 |
17,38403 |
-0,23109 |
| 0,0004 |
25,35179 |
-0,2205 |
| 0,0005 |
33,29965 |
-0,2089 |
| 0,0006 |
41,31696 |
-0,19639 |
| 0,0007 |
49,53572 |
-0,1831 |
| 0,0008 |
58,0041 |
-0,16918 |
| 0,0009 |
66,66728 |
-0,15481 |
| 0,001 |
75,47651 |
-0,1402 |
| 0,0011 |
84,49494 |
-0,12555 |
| 0,0012 |
93,87112 |
-0,1111 |
| 0,0013 |
103,7081 |
-0,09706 |
| 0,0014 |
113,987 |
-0,08363 |
| 0,0015 |
124,6508 |
-0,071 |
| 0,0016 |
135,7634 |
-0,05932 |
| 0,0017 |
147,546 |
-0,04873 |
| 0,0018 |
160,1973 |
-0,03929 |
| 0,0019 |
173,6352 |
-0,03106 |
| 0,002 |
187,4073 |
-0,02404 |
| 0,0021 |
200,8812 |
-0,01819 |
| 0,0022 |
213,5618 |
-0,01344 |
| 0,0023 |
225,2688 |
-0,0097 |
| 0,0024 |
236,0464 |
-0,00683 |
| 0,0025 |
245,9361 |
-0,00471 |
| 0,0026 |
254,855 |
-0,0032 |
| 0,0027 |
262,6779 |
-0,00215 |
| 0,0028 |
269,3953 |
-0,00144 |
| 0,0029 |
275,1464 |
-0,00095 |
| 0,003 |
280,0859 |
-0,0006 |
| 0,0031 |
284,2435 |
-0,0003 |
| 0,0032 |
287,5559 |
-1,9Е-05 |
| 0,0033 |
290,0634 |
0,000277 |
| 0,0034 |
292,0671 |
0,000595 |
| 0,0035 |
294,061 |
0,000928 |
| 0,0036 |
296,4683 |
0,001258 |
| 0,0037 |
299,4047 |
0,001566 |
| 0,0038 |
302,6652 |
0,001832 |
| 0,0039 |
305,9184 |
0,002043 |
Продолжение табл.1
Способ определения амплитуды и фазы эквивалентной синусоиды тока в цепи с ферромагнитным сердечником |
| 1 |
2 |
3 |
| 0,004 |
308,9105 |
0,0022 |
| 0,0041 |
311,5178 |
0,002315 |
| 0,0042 |
313,6685 |
0,002417 |
| 0,0043 |
315,2815 |
0,002548 |
| 0,0044 |
316,3144 |
0,002767 |
| 0,0045 |
316,847 |
0,003142 |
| 0,0046 |
317,0705 |
0,003749 |
| 0,0047 |
317,1554 |
0,004664 |
| 0,0048 |
317,1292 |
0,005962 |
| 0,0049 |
316,9013 |
0,007708 |
| 0,005 |
316,4158 |
0,009955 |
| 0,0051 |
315,7609 |
0,012739 |
| 0,0052 |
315,0939 |
0,016077 |
| 0,0053 |
314,4419 |
0,019966 |
| 0,0054 |
313,5893 |
0,024382 |
| 0,0055 |
312,195 |
0,029284 |
| 0,0056 |
310,0522 |
0,034618 |
| 0,0057 |
307,2465 |
0,040317 |
| 0,0058 |
304,0602 |
0,04631 |
| 0,0059 |
300,7214 |
0,052526 |
| 0,006 |
297,2444 |
0,058897 |
| 0,0061 |
293,503 |
0,065368 |
| 0,0062 |
289,4326 |
0,071896 |
| 0,0063 |
285,127 |
0,078453 |
| 0,0064 |
280,7248 |
0,08503 |
| 0,0065 |
276,2222 |
0,091634 |
| 0,0066 |
271,442 |
0,098288 |
| 0,0067 |
266,2276 |
0,105027 |
| 0,0068 |
260,6846 |
0,111894 |
| 0,0069 |
255,2164 |
0,118935 |
| 0,007 |
250,2833 |
0,126196 |
| 0,0071 |
246,0762 |
0,133713 |
| 0,0072 |
242,3706 |
0,141513 |
| 0,0073 |
238,6626 |
0,149606 |
| 0,0074 |
234,4483 |
0,157985 |
| 0,0075 |
229,4243 |
0,166622 |
| 0,0076 |
223,5137 |
0,17547 |
| 0,0077 |
216,7831 |
0,184465 |
| 0,0078 |
209,3601 |
0,193524 |
| 0,0079 |
201,3727 |
0,202555 |
| 0,008 |
192,8698 |
0,211457 |
| 0,0081 |
183,732 |
0,220127 |
Продолжение табл.1
Способ определения амплитуды и фазы эквивалентной синусоиды тока в цепи с ферромагнитным сердечником |
| 1 |
2 |
3 |
| 0,0082 |
173,6791 |
0,22846 |
| 0,0083 |
162,4602 |
0,236361 |
| 0,0084 |
150,1452 |
0,243742 |
| 0,0085 |
137,2791 |
0,250526 |
| 0,0086 |
124,7116 |
0,256652 |
| 0,0087 |
113,1721 |
0,262068 |
| 0,0088 |
102,8996 |
0,266737 |
| 0,0089 |
93,61623 |
0,270633 |
| 0,009 |
84,84347 |
0,273733 |
| 0,0091 |
76,27708 |
0,276023 |
| 0,0092 |
67,91262 |
0,277486 |
| 0,0093 |
59,87207 |
0,278106 |
| 0,0094 |
52,15683 |
0,27786 |
| 0,0095 |
44,58359 |
0,276721 |
| 0,0096 |
36,93995 |
0,274654 |
| 0,0097 |
29,16776 |
0,27162 |
| 0,0098 |
21,37528 |
0,267577 |
| 0,0099 |
13,68031 |
0,262484 |
| 0,01 |
6,065752 |
0,256306 |
| 0,0101 |
-1,60001 |
0,249016 |
| 0,0102 |
-9,41676 |
0,240607 |
| 0,0103 |
-17,3535 |
0,231088 |
| 0,0104 |
-25,3056 |
0,220497 |
| 0,0105 |
-33,2353 |
0,208899 |
| 0,0106 |
-41,2325 |
0,196391 |
| 0,0107 |
-49,4296 |
0,183098 |
| 0,0108 |
-57,8751 |
0,169176 |
| 0,0109 |
-66,5149 |
0,154809 |
| 0,011 |
-75,3006 |
0,140196 |
| 0,0111 |
-84,296 |
0,125554 |
| 0,0112 |
-93,6501 |
0,111102 |
| 0,0113 |
-103,466 |
0,097059 |
| 0,0114 |
-113,727 |
0,08363 |
| 0,0115 |
-124,375 |
0,070999 |
| 0,0116 |
-135,474 |
0,059323 |
| 0,0117 |
-147,247 |
0,048726 |
| 0,0118 |
-159,892 |
0,039291 |
| 0,0119 |
-173,328 |
0,031062 |
| 0,012 |
-187,103 |
0,02404 |
| 0,0121 |
-200,584 |
0,018192 |
| 0,0122 |
-213,276 |
0,013444 |
| 0,0123 |
-224,999 |
0,009698 |
| 0,0124 |
-235,798 |
0,006833 |
| 0,0125 |
-245,713 |
0,004713 |
Продолжение табл.1
Способ определения амплитуды и фазы эквивалентной синусоиды тока в цепи с ферромагнитным сердечником |
| 1 |
2 |
3 |
| 0,0126 |
-254,661 |
0,003198 |
| 0,0127 |
-262,518 |
0,002149 |
| 0,0128 |
-269,272 |
0,001438 |
| 0,0129 |
-275,064 |
0,000952 |
| 0,013 |
-280,048 |
0,000597 |
| 0,0131 |
-284,251 |
0,000302 |
| 0,0132 |
-287,612 |
1,94Е-05 |
| 0,0133 |
-290,169 |
-0,00028 |
| 0,0134 |
-292,222 |
-0,0006 |
| 0,0135 |
-294,266 |
-0,00093 |
| 0,0136 |
-296,723 |
-0,00126 |
| 0,0137 |
-299,708 |
-0,00157 |
| 0,0138 |
-303,015 |
-0,00183 |
| 0,0139 |
-306,312 |
-0,00204 |
| 0,014 |
-309,346 |
-0,0022 |
| 0,0141 |
-311,99 |
-0,00232 |
| 0,0142 |
-314,174 |
-0,00242 |
| 0,0143 |
-315,816 |
-0,00255 |
| 0,0144 |
-316,873 |
-0,00277 |
| 0,0145 |
-317,424 |
-0,00314 |
| 0,0146 |
-317,66 |
-0,00375 |
| 0,0147 |
-317,753 |
-0,00466 |
| 0,0148 |
-317,728 |
-0,00596 |
| 0,0149 |
-317,495 |
-0,00771 |
| 0,015 |
-316,999 |
-0,00996 |
| 0,0151 |
-316,328 |
-0,01274 |
| 0,0152 |
-315,639 |
-0,01608 |
| 0,0153 |
-314,96 |
-0,01997 |
| 0,0154 |
-314,076 |
-0,02438 |
| 0,0155 |
-312,645 |
-0,02928 |
| 0,0156 |
-310,462 |
-0,03462 |
| 0,0157 |
-307,612 |
-0,04032 |
| 0,0158 |
-304,379 |
-0,04631 |
| 0,0159 |
-300,99 |
-0,05253 |
| 0,016 |
-297,462 |
-0,0589 |
| 0,0161 |
-293,668 |
-0,06537 |
| 0,0162 |
-289,545 |
-0,0719 |
| 0,0163 |
-285,187 |
-0,07845 |
| 0,0164 |
-280,733 |
-0,08503 |
| 0,0165 |
-276,18 |
-0,09163 |
| 0,0166 |
-271,352 |
-0,09829 |
| 0,0167 |
-266,092 |
-0,10503 |
| 0,0168 |
-260,507 |
-0,11189 |
| 0,0169 |
-254,999 |
-0,11894 |
Окончание табл.1
Способ определения амплитуды и фазы эквивалентной синусоиды тока в цепи с ферромагнитным сердечником |
| 1 |
2 |
3 |
| 0,017 |
-250,031 |
-0,1262 |
| 0,0171 |
-245,794 |
-0,13371 |
| 0,0172 |
-242,062 |
-0,14151 |
| 0,0173 |
-238,332 |
-0,14961 |
| 0,0174 |
-234,101 |
-0,15798 |
| 0,0175 |
-229,066 |
-0,16662 |
| 0,0176 |
-223,148 |
-0,17547 |
| 0,0177 |
-216,416 |
-0,18446 |
| 0,0178 |
-208,995 |
-0,19352 |
| 0,0179 |
-201,015 |
-0,20256 |
| 0,018 |
-192,522 |
-0,21146 |
| 0,0181 |
-183,399 |
-0,22013 |
| 0,0182 |
-173,364 |
-0,22846 |
| 0,0183 |
-162,166 |
-0,23636 |
| 0,0184 |
-149,873 |
-0,24374 |
| 0,0185 |
-137,032 |
-0,25053 |
| 0,0186 |
-124,49 |
-0,25665 |
| 0,0187 |
-112,977 |
-0,26207 |
| 0,0188 |
-102,731 |
-0,26674 |
| 0,0189 |
-93,4738 |
-0,27063 |
| 0,019 |
-84,7263 |
-0,27373 |
| 0,0191 |
-76,1837 |
-0,27602 |
| 0,0192 |
-67,8412 |
-0,27749 |
| 0,0193 |
-59,8203 |
-0,27811 |
| 0,0194 |
-52,1221 |
-0,27786 |
| 0,0195 |
-44,5629 |
-0,27672 |
| 0,0196 |
-36,9301 |
-0,27465 |
| 0,0197 |
-29,1653 |
-0,27162 |
| 0,0198 |
-21,3768 |
-0,26758 |
| 0,0199 |
-13,6822 |
-0,26248 |
| 0,02 |
-6,06453 |
-0,25631 |
Табл.2
Способ определения амплитуды и фазы эквивалентной синусоиды тока в цепи с ферромагнитным сердечником |
| Время, t, c |
u(tj), В |
I(tj), A |
| 1 |
2 |
3 |
| 0 |
-6,06453 |
-0,20366 |
| 0,0001 |
1,607813 |
-0,20153 |
| 0,0002 |
9,434411 |
-0,19919 |
| 0,0003 |
17,38403 |
-0,19666 |
| 0,0004 |
25,35179 |
-0,19394 |
| 0,0005 |
33,29965 |
-0,19102 |
| 0,0006 |
41,31696 |
-0,18792 |
| 0,0007 |
49,53572 |
-0,18463 |
| 0,0008 |
58,0041 |
-0,18116 |
| 0,0009 |
66,66728 |
-0,17751 |
| 0,001 |
75,47651 |
-0,17368 |
| 0,0011 |
84,49494 |
-0,16968 |
| 0,0012 |
93,87112 |
-0,16552 |
| 0,0013 |
103,7081 |
-0,16119 |
| 0,0014 |
113,987 |
-0,15671 |
| 0,0015 |
124,6508 |
-0,15206 |
| 0,0016 |
135,7634 |
-0,14727 |
| 0,0017 |
147,546 |
-0,14234 |
| 0,0018 |
160,1973 |
-0,13726 |
| 0,0019 |
173,6352 |
-0,13205 |
| 0,002 |
187,4073 |
-0,1267 |
| 0.0021 |
200,8812 |
-0,12123 |
| 0,0022 |
213,5618 |
-0,11565 |
| 0,0023 |
225,2688 |
-0,10994 |
| 0,0024 |
236,0464 |
-0,10413 |
| 0,0025 |
245,9361 |
-0,09822 |
| 0,0026 |
254,855 |
-0,09221 |
| 0,0027 |
262,6779 |
-0,08611 |
| 0,0028 |
269,3953 |
-0,07992 |
| 0,0029 |
275,1464 |
-0,07366 |
| 0,003 |
280,0859 |
-0,06732 |
| 0,0031 |
284,2435 |
-0,06092 |
| 0,0032 |
287,5559 |
-0,05445 |
| 0,0033 |
290,0634 |
-0,04793 |
| 0,0034 |
292,0671 |
-0,04137 |
| 0,0035 |
294,061 |
-0,03476 |
| 0,0036 |
296,4683 |
-0,02812 |
| 0,0037 |
299,4047 |
-0,02145 |
| 0,0038 |
302,6652 |
-0,01476 |
| 0,0039 |
305,9184 |
-0,00806 |
Продолжение табл.2
Способ определения амплитуды и фазы эквивалентной синусоиды тока в цепи с ферромагнитным сердечником |
| 1 |
2 |
3 |
| 0,004 |
308,9105 |
-0,00135 |
| 0,0041 |
311,5178 |
0,005365 |
| 0,0042 |
313,6685 |
0,012073 |
| 0,0043 |
315,2815 |
0,018769 |
| 0,0044 |
316,3144 |
0,025446 |
| 0,0045 |
316,847 |
0,032099 |
| 0,0046 |
317,0705 |
0,03872 |
| 0,0047 |
317,1554 |
0,045302 |
| 0,0048 |
317,1292 |
0,05184 |
| 0,0049 |
316,9013 |
0,058326 |
| 0,005 |
316,4158 |
0,064756 |
| 0,0051 |
315,7609 |
0,071121 |
| 0,0052 |
315,0939 |
0,077416 |
| 0,0053 |
314,4419 |
0,083634 |
| 0,0054 |
313,5893 |
0,08977 |
| 0,0055 |
312,195 |
0,095818 |
| 0,0056 |
310,0522 |
0,101771 |
| 0,0057 |
307,2465 |
0,107623 |
| 0,0058 |
304,0602 |
0,113369 |
| 0,0059 |
300,7214 |
0,119004 |
| 0,006 |
297,2444 |
0,124521 |
| 0,0061 |
293,503 |
0,129915 |
| 0,0062 |
289,4326 |
0,13518 |
| 0,0063 |
285,127 |
0,140313 |
| 0,0064 |
280,7248 |
0,145307 |
| 0,0065 |
276,2222 |
0,150157 |
| 0,0066 |
271,442 |
0,15486 |
| 0,0067 |
266,2276 |
0,159409 |
| 0,0068 |
260,6846 |
0,163801 |
| 0,0069 |
255,2164 |
0,168032 |
| 0,007 |
250,2833 |
0,172097 |
| 0,0071 |
246,0762 |
0,175992 |
| 0,0072 |
242,3706 |
0,179713 |
| 0,0073 |
238,6626 |
0,183257 |
| 0,0074 |
234,4483 |
0,18662 |
| 0,0075 |
229,4243 |
0,189798 |
| 0,0076 |
223,5137 |
0,19279 |
| 0,0077 |
216,7831 |
0,195591 |
| 0,0078 |
209,3601 |
0,198199 |
| 0,0079 |
201,3727 |
0,200612 |
| 0,008 |
192,8698 |
0,202827 |
| 0,0081 |
183,732 |
0,204841 |
Продолжение табл.2
Способ определения амплитуды и фазы эквивалентной синусоиды тока в цепи с ферромагнитным сердечником |
| 1 |
2 |
3 |
| 0,0082 |
173,6791 |
0,206654 |
| 0,0083 |
162,4602 |
0,208262 |
| 0,0084 |
150,1452 |
0,209665 |
| 0,0085 |
137,2791 |
0,210861 |
| 0,0086 |
124,7116 |
0,211849 |
| 0,0087 |
113,1721 |
0,212627 |
| 0,0088 |
102,8996 |
0,213196 |
| 0,0089 |
93,61623 |
0,213555 |
| 0,009 |
84,84347 |
0,213703 |
| 0,0091 |
76,27708 |
0,21364 |
| 0,0092 |
67,91262 |
0,213366 |
| 0,0093 |
59,87207 |
0,212881 |
| 0,0094 |
52,15683 |
0,212187 |
| 0,0095 |
44,58359 |
0,211283 |
| 0,0096 |
36,93995 |
0,21017 |
| 0,0097 |
29,16776 |
0,20885 |
| 0,0098 |
21,37528 |
0,207324 |
| 0,0099 |
13,68031 |
0,205594 |
| 0,01 |
6,065752 |
0,20366 |
| 0,0101 |
-1,60001 |
0,201526 |
| 0,0102 |
-9,41676 |
0,199192 |
| 0,0103 |
-17,3535 |
0,196662 |
| 0,0104 |
-25,3056 |
0,193938 |
| 0,0105 |
-33,2353 |
0,191023 |
| 0,0106 |
-41,2325 |
0,187919 |
| 0,0107 |
-49,4296 |
0,184629 |
| 0,0108 |
-57,8751 |
0,181158 |
| 0,0109 |
-66,5149 |
0,177507 |
| 0,011 |
-75,3006 |
0,173682 |
| 0,0111 |
-84,296 |
0,169685 |
| 0,0112 |
-93,6501 |
0,16552 |
| 0,0113 |
-103,466 |
0,161192 |
| 0,0114 |
-113,727 |
0,156706 |
| 0,0115 |
-124,375 |
0,152064 |
| 0,0116 |
-135,474 |
0,147272 |
| 0,0117 |
-147,247 |
0,142336 |
| 0,0118 |
-159,892 |
0,137258 |
| 0,0119 |
-173,328 |
0,132045 |
| 0,012 |
-187,103 |
0,126702 |
| 0,0121 |
-200,584 |
0,121234 |
| 0,0122 |
-213,276 |
0,115646 |
| 0,0123 |
-224,999 |
0,109944 |
| 0,0124 |
-235,798 |
0,104134 |
| 0,0125 |
-245,713 |
0,09822 |
Продолжение табл.2
Способ определения амплитуды и фазы эквивалентной синусоиды тока в цепи с ферромагнитным сердечником |
| 1 |
2 |
3 |
| 0,0126 |
-254,661 |
0,09221 |
| 0,0127 |
-262,518 |
0,086109 |
| 0,0128 |
-269,272 |
0,079923 |
| 0,0129 |
-275,064 |
0,073658 |
| 0,013 |
-280,048 |
0,06732 |
| 0,0131 |
-284,251 |
0,060916 |
| 0,0132 |
-287,612 |
0,054452 |
| 0,0133 |
-290,169 |
0,047934 |
| 0,0134 |
-292,222 |
0,041368 |
| 0,0135 |
-294,266 |
0,034762 |
| 0,0136 |
-296,723 |
0,028122 |
| 0,0137 |
-299,708 |
0,021453 |
| 0,0138 |
-303,015 |
0,014764 |
| 0,0139 |
-306,312 |
0,00806 |
| 0,014 |
-309,346 |
0,001348 |
| 0,0141 |
-311,99 |
-0,00536 |
| 0,0142 |
-314,174 |
-0,01207 |
| 0,0143 |
-315,816 |
-0,01877 |
| 0,0144 |
-316,873 |
-0,02545 |
| 0,0145 |
-317,424 |
-0,0321 |
| 0,0146 |
-317,66 |
-0,03872 |
| 0,0147 |
-317,753 |
-0,0453 |
| 0,0148 |
-317,728 |
-0,05184 |
| 0,0149 |
-317,495 |
-0,05833 |
| 0,015 |
-316,999 |
-0,06476 |
| 0,0151 |
-316,328 |
-0,07112 |
| 0,0152 |
-315,639 |
-0,07742 |
| 0,0153 |
-314,96 |
-0,08363 |
| 0,0154 |
-314,076 |
-0,08977 |
| 0,0155 |
-312,645 |
-0,09582 |
| 0,0156 |
-310,462 |
-0,10177 |
| 0,0157 |
-307,612 |
-0,10762 |
| 0,0158 |
-304,379 |
-0,11337 |
| 0,0159 |
-300,99 |
-0,119 |
| 0,016 |
-297,462 |
-0,12452 |
| 0,0161 |
-293,668 |
-0,12991 |
| 0,0162 |
-289,545 |
-0,13518 |
| 0,0163 |
-285,187 |
-0,14031 |
| 0,0164 |
-280,733 |
-0,14531 |
| 0,0165 |
-276,18 |
-0,15016 |
| 0,0166 |
-271,352 |
-0,15486 |
| 0,0167 |
-266,092 |
-0,15941 |
| 0,0168 |
-260,507 |
-0,1638 |
| 0,0169 |
-254,999 |
-0,16803 |
Окончание табл.2
Способ определения амплитуды и фазы эквивалентной синусоиды тока в цепи с ферромагнитным сердечником |
| 1 |
2 |
3 |
| 0,017 |
-250,031 |
-0,1721 |
| 0,0171 |
-245,794 |
-0,17599 |
| 0,0172 |
-242,062 |
-0,17971 |
| 0,0173 |
-238,332 |
-0,18326 |
| 0,0174 |
-234,101 |
-0,18662 |
| 0,0175 |
-229,066 |
-0,1898 |
| 0,0176 |
-223,148 |
-0,19279 |
| 0,0177 |
-216,416 |
-0,19559 |
| 0,0178 |
-208,995 |
-0,1982 |
| 0,0179 |
-201,015 |
-0,20061 |
| 0,018 |
-192,522 |
-0,20283 |
| 0,0181 |
-183,399 |
-0,20484 |
| 0,0182 |
-173,364 |
-0,20665 |
| 0,0183 |
-162,166 |
-0,20826 |
| 0,0184 |
-149,873 |
-0,20966 |
| 0,0185 |
-137,032 |
-0,21086 |
| 0,0186 |
-124,49 |
-0,21185 |
| 0,0187 |
-112,977 |
-0,21263 |
| 0,0188 |
-102,731 |
-0,2132 |
| 0,0189 |
-93,4738 |
-0,21355 |
| 0,019 |
-84,7263 |
-0,2137 |
| 0,0191 |
-76,1837 |
-0,21364 |
| 0,0192 |
-67,8412 |
-0,21337 |
| 0,0193 |
-59,8203 |
-0,21288 |
| 0,0194 |
-52,1221 |
-0,21219 |
| 0,0195 |
-44,5629 |
-0,21128 |
| 0,0196 |
-36,9301 |
-0,21017 |
| 0,0197 |
-29,1653 |
-0,20885 |
| 0,0198 |
-21,3768 |
-0,20732 |
| 0,0199 |
-13,6822 |
-0,20559 |
| 0,02 |
-6,06453 |
-0,20366 |
Формула изобретения
Способ определения амплитуды и фазы эквивалентной синусоиды тока в цепи с ферромагнитным сердечником, включающий измерение мгновенных значений синусоидального питающего напряжения и несинусоидального тока и определение амплитуды эквивалентной синусоиды тока, отличающийся тем, что для сигналов синусоидального питающего напряжения u(tj) и несинусоидального тока i(tj), представленных цифровыми отсчетами мгновенных значений для одних и тех же моментов времени tj=t1, t2,…, tN, где N – число разбиений на периоде Т, с помощью программатора действующих значений определяют их действующие значения по выражениям
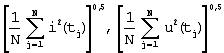
затем с помощью программатора мощности определяют активную (среднюю за период) мощность из выражения
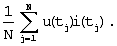
далее с помощью делителя определяют фазу эквивалентной синусоиды по выражению
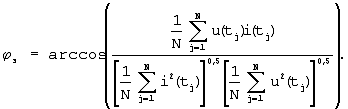
РИСУНКИ
MM4A – Досрочное прекращение действия патента СССР или патента Российской Федерации на изобретение из-за неуплаты в установленный срок пошлины за поддержание патента в силе
Дата прекращения действия патента: 09.01.2006
Извещение опубликовано: 20.09.2007 БИ: 26/2007
|
|